Meta-Deflectors Made of Dielectric Nanohole Arrays with Anti-Damage Potential
Abstract
:1. Introduction
2. Materials and Methods
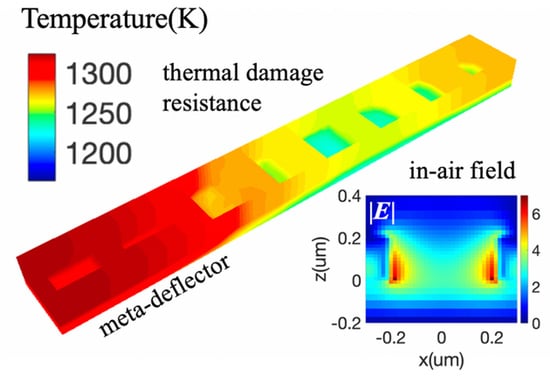
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Manes, K.; Spaeth, M.; Adams, J.; Bowers, M. Damage Mechanisms Avoided or Managed for NIF Large Optics. Fusion Sci. Technol. 2016, 69, 146–249. [Google Scholar] [CrossRef]
- Li, C.; Sun, Y.; Song, X.; Zhang, X.; Shi, Z.; Wang, F.; Ye, X.; Chen, S.; Sun, L.; Huang, J. Capping a glass thin layer on the etched surface via plasma chemical vapor deposition for improving the laser damage performance of fused silica. Opt. Express 2019, 27, 2268–2280. [Google Scholar] [CrossRef] [PubMed]
- Laixi, S.; Jin, H.; Hongjie, L.; Xin, Y.; Jingjun, W.; Xiaodong, J.; Liming, Y.; Wanguo, Z.; Weidong, W. Combination of reaction ion etching and dynamic chemical etching for improving laser damage resistance of fused silica optical surfaces. Opt. Lett. 2016, 41, 4464. [Google Scholar]
- Li, C.; Li, Q.; Sun, L.; Ye, X.; Chen, S.; Wu, Z.; Huang, J.; Wu, W.; Jiang, X. Effect of PVA coating on the electric field intensity distribution and laser damage performance of fused silica optics surfaces. Opt. Express 2018, 26, 19707–19717. [Google Scholar] [CrossRef] [PubMed]
- Ye, X.; Hu, X.; Tang, F.; Wu, J.; Yang, L.; Huang, J.; Zheng, W. Laser Field Manipulation and Laser Damage Resistance Property of Nanotextures on Fused Silica Optics. Results Phys. 2020, 18, 103262. [Google Scholar] [CrossRef]
- Jing, X.; Tian, Y.; Han, J.; Ma, J.; Jin, Y.; Shao, J.; Fan, Z. Polarization effect of femtosecond pulse breakdown in subwavelength antireflective relief grating. Opt. Commun. 2011, 284, 4220–4224. [Google Scholar] [CrossRef]
- Glybovski, S.B.; Tretyakov, S.A.; Belov, P.A.; Kivshar, Y.S.; Simovski, C.R. Metasurfaces: From microwaves to visible. Phys. Rep. 2016, 634, 1–72. [Google Scholar] [CrossRef]
- Genevet, P.; Capasso, F.; Aieta, F.; Khorasaninejad, M.; Devlin, R. Recent advances in planar optics: From plasmonic to dielectric metasurfaces. Optica 2017, 4, 139–152. [Google Scholar] [CrossRef]
- Hou-Tong, C.; Antoinette, J.T.; Nanfang, Y. A review of metasurfaces: Physics and applications. Rep. Prog. Phys. 2016, 79, 076401. [Google Scholar]
- Jahani, S.; Jacob, Z. All-dielectric metamaterials. Nat. Nanotechnol. 2016, 11, 23. [Google Scholar] [CrossRef]
- Hsiao, H.-H.; Chu, C.H.; Tsai, D.P. Fundamentals and Applications of Metasurfaces. Small Methods 2017, 1, 1600064. [Google Scholar] [CrossRef] [Green Version]
- Liu, L.; Zhang, X.; Kenney, M.; Su, X.; Xu, N.; Ouyang, C.; Shi, Y.; Han, J.; Zhang, W.; Zhang, S. Broadband Metasurfaces with Simultaneous Control of Phase and Amplitude. Adv. Mater. 2014, 26, 5031–5036. [Google Scholar] [CrossRef] [PubMed]
- Pors, A.; Bozhevolnyi, S.I. Gap plasmon-based phase-amplitude metasurfaces: Material constraints [Invited]. Opt. Mater. Express 2015, 5, 2448–2458. [Google Scholar] [CrossRef] [Green Version]
- Wu, J.; Tang, F.; Ma, J.; Li, Q.; Shang, S.; Chen, J.; Wu, Y.; Wang, Y.; Ye, X.; Zheng, W.; et al. Angle-sensitive dynamic optical modulation based on Huygens metasurfaces. Results Phys. 2020, 18, 103226. [Google Scholar] [CrossRef]
- Kwon, D.H.; Ptitcyn, G.; Díaz-Rubio, A.; Tretyakov, S.A. Transmission Magnitude and Phase Control for Polarization-Preserving Reflectionless Metasurfaces. Phys. Rev. Appl. 2018, 9, 034005. [Google Scholar] [CrossRef] [Green Version]
- Lingling, H.; Shuang, Z.; Thomas, Z. Metasurface holography: From fundamentals to applications. Nanophotonics 2018, 7, 1169–1190. [Google Scholar] [CrossRef]
- Shalaev, M.I.; Sun, J.; Tsukernik, A.; Pandey, A.; Nikolskiy, K.; Litchinitser, N.M. High-Efficiency All-Dielectric Metasurfaces for Ultracompact Beam Manipulation in Transmission Mode. Nano Lett. 2015, 15, 6261–6266. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Decker, M.; Staude, I.; Falkner, M.; Dominguez, J.; Neshev, D.N.; Brener, I.; Pertsch, T.; Kivshar, Y.S. High-Efficiency Dielectric Huygens’ Surfaces. Adv. Opt. Mater. 2015, 3, 813–820. [Google Scholar] [CrossRef] [Green Version]
- Pors, A.; Nielsen, M.G.; Bernardin, T.; Weeber, J.-C.; Bozhevolnyi, S.I. Efficient unidirectional polarization-controlled excitation of surface plasmon polaritons. Light Sci. Appl. 2014, 3, e197. [Google Scholar] [CrossRef] [Green Version]
- Khorasaninejad, M.; Chen, W.T.; Zhu, A.Y.; Oh, J.; Devlin, R.C.; Rousso, D.; Capasso, F. Multispectral Chiral Imaging with a Metalens. Nano Lett. 2016, 16, 4595–4600. [Google Scholar] [CrossRef]
- Segal, N.; Keren-Zur, S.; Hendler, N.; Ellenbogen, T. Controlling light with metamaterial-based nonlinear photonic crystals. Nat. Photonics 2015, 9, 180. [Google Scholar] [CrossRef]
- Husu, H.; Siikanen, R.; Mäkitalo, J.; Lehtolahti, J.; Laukkanen, J.; Kuittinen, M.; Kauranen, M. Metamaterials with Tailored Nonlinear Optical Response. Nano Lett. 2012, 12, 673–677. [Google Scholar] [CrossRef]
- Chu, P.; Chen, J.; Xiong, Z.; Yi, Z. Controllable frequency conversion in the coupled time-modulated cavities with phase delay. Opt. Commun. 2020, 476, 126338. [Google Scholar] [CrossRef]
- Monti, A.; Alù, A.; Toscano, A.; Bilotti, F. Surface Impedance Modeling of All-Dielectric Metasurfaces. IEEE Trans. Antennas Propag. 2020, 68, 1799–1811. [Google Scholar] [CrossRef]
- Moitra, P.; Slovick, B.A.; Li, W.; Kravchencko, I.I.; Briggs, D.P.; Krishnamurthy, S.; Valentine, J. Large-Scale All-Dielectric Metamaterial Perfect Reflectors. ACS Photonics 2015, 2, 692–698. [Google Scholar] [CrossRef]
- Lin, R.J.; Su, V.-C.; Wang, S.; Chen, M.K.; Chung, T.L.; Chen, Y.H.; Kuo, H.Y.; Chen, J.-W.; Chen, J.; Huang, Y.-T.; et al. Achromatic metalens array for full-colour light-field imaging. Nat. Nanotechnol. 2019, 14, 227–231. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Divitt, S.; Fan, Q.; Zhu, W.; Agrawal, A.; Xu, T.; Lezec, H.J. All-dielectric Deep Ultraviolet Metasurfaces. In CLEO: QELS_Fundamental Science; Optical Society of America: Washington, DC, USA, 2019; p. FM3C–3. [Google Scholar]
- Tang, F.; Ye, X.; Li, Q.; Wang, Y.; Yu, H.; Wu, W.; Li, B.; Zheng, W. Dielectric Metalenses at Long-wave Infrared Wavelengths: Multiplexing and Spectroscope. Results Phys. 2020, 18, 103215. [Google Scholar] [CrossRef]
- Khorasaninejad, M.; Capasso, F. Broadband Multifunctional Efficient Meta-Gratings Based on Dielectric Waveguide Phase Shifters. Nano Lett. 2015, 15, 6709–6715. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; Tang, F.; Chen, J.; Shang, S.; Wu, J.; Chen, S.; Chen, Y.; Ye, X.; Yang, L. Design of high-efficiency all-dielectric polymer meta-surfaces beam deflection blazed grating. Results Phys. 2020, 17, 103094. [Google Scholar] [CrossRef]
- Yu, Y.F.; Zhu, A.Y.; Paniagua-Domínguez, R.; Fu, Y.H.; Luk’yanchuk, B.; Kuznetsov, A.I. High-transmission dielectric metasurface with 2π phase control at visible wavelengths. Laser Photon. Rev. 2015, 9, 412–418. [Google Scholar] [CrossRef]
- Yi, Z.; Li, J.; Lin, J.; Qin, F.; Chen, X.; Yao, W.-T.; Liu, Z.; Cheng, S.; Wu, P.; Li, H. Broadband polarization-insensitive and wide-angle solar energy absorber based on tungsten ring-disc array. Nanoscale 2020, 12, 23077–23083. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Wu, P.; Zhou, Z.; Chen, X.; Yi, Z.; Zhu, J.; Zhang, T.; Jile, H. Study on temperature adjustable terahertz metamaterial absorber based on vanadium dioxide. IEEE Access 2020, 8, 85154–85161. [Google Scholar] [CrossRef]
- Zhao, F.; Chen, X.; Yi, Z.; Qin, F.; Tang, Y.; Yao, W.; Zhou, Z.; Yi, Y. Study on the solar energy absorption of hybrid solar cells with trapezoid-pyramidal structure based PEDOT: PSS/c-Ge. Sol. Energy 2020, 204, 635–643. [Google Scholar] [CrossRef]
- Yu, P.; Yang, H.; Chen, X.; Yi, Z.; Yao, W.; Chen, J.; Yi, Y.; Wu, P. Ultra-wideband solar absorber based on refractory titanium metal. Renew. Energy 2020, 158, 227–235. [Google Scholar] [CrossRef]
- Chen, T.; Chang, F.; Huang, B.; Yu, P. Optical absorption enhancement in silicon nanohole arrays for photovoltaics. In Proceedings of the 2011 37th IEEE Photovoltaic Specialists Conference, Seattle, WA, USA, 19–24 June 2011; pp. 002855–002857. [Google Scholar]
- Xia, Z.; Qin, X.; Wu, Y.; Pan, Y.; Zhou, J.; Zhang, Z. Efficient broadband light absorption in elliptical nanohole arrays for photovoltaic application. Opt. Lett. 2015, 40, 5814–5817. [Google Scholar] [CrossRef]
- Sun, S.; Zhou, Z.; Zhang, C.; Gao, Y.; Duan, Z.; Xiao, S.; Song, Q. All-Dielectric Full-Color Printing with TiO2 Metasurfaces. ACS Nano 2017, 11, 4445–4452. [Google Scholar] [CrossRef] [PubMed]
- Zhao, W.; Jiang, H.; Liu, B.; Song, J.; Jiang, Y.; Tang, C.; Li, J. Dielectric Huygens’ Metasurface for High-Efficiency Hologram Operating in Transmission Mode. Sci. Rep. 2016, 6, 30613. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Geffrin, J.M.; García-Cámara, B.; Gómez-Medina, R.; Albella, P.; Froufe-Pérez, L.S.; Eyraud, C.; Litman, A.; Vaillon, R.; González, F.; Nieto-Vesperinas, M.; et al. Magnetic and electric coherence in forward- and back-scattered electromagnetic waves by a single dielectric subwavelength sphere. Nat. Commun. 2012, 3, 1171. [Google Scholar] [CrossRef] [PubMed]






| Phase Point | 0 | π/4 | π/2 | 3π/4 | π | 5π/4 | 3π/2 | 7π/4 |
|---|---|---|---|---|---|---|---|---|
| Phase offset | 0.012 | 0.059 | 0.052 | 0.055 | 0.07 | 0.207 | 0.183 | 0.072 |
| Reflectance | 0.995 | 0.949 | 0.945 | 0.733 | 0.38 | 0.796 | 0.992 | 0.994 |
| W(nm) | 425 | 500 | 355 | 270 | 485 | 460 | 430 | 425 |
| L(nm) | 365 | 260 | 555 | 555 | 550 | 520 | 525 | 425 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, H.; Tang, F.; Wu, J.; Yi, Z.; Ye, X.; Wang, Y. Meta-Deflectors Made of Dielectric Nanohole Arrays with Anti-Damage Potential. Photonics 2021, 8, 107. https://doi.org/10.3390/photonics8040107
Yu H, Tang F, Wu J, Yi Z, Ye X, Wang Y. Meta-Deflectors Made of Dielectric Nanohole Arrays with Anti-Damage Potential. Photonics. 2021; 8(4):107. https://doi.org/10.3390/photonics8040107
Chicago/Turabian StyleYu, Haichao, Feng Tang, Jingjun Wu, Zao Yi, Xin Ye, and Yiqun Wang. 2021. "Meta-Deflectors Made of Dielectric Nanohole Arrays with Anti-Damage Potential" Photonics 8, no. 4: 107. https://doi.org/10.3390/photonics8040107
APA StyleYu, H., Tang, F., Wu, J., Yi, Z., Ye, X., & Wang, Y. (2021). Meta-Deflectors Made of Dielectric Nanohole Arrays with Anti-Damage Potential. Photonics, 8(4), 107. https://doi.org/10.3390/photonics8040107