A Single-Stack Output Power Prediction Method for High-Power, Multi-Stack SOFC System Requirements
Abstract
:1. Introduction
- The prediction for SOFC output power utilizes the combustion chamber temperature, stack temperature, and electrical current as input parameters, with the output power being the output parameter. This approach is more comprehensive than traditional approaches to predictive modeling that rely solely on the inputs and outputs of the stack.
- The suggested GA-BP algorithm notably enhances the precision of output power prediction in a SOFC system, thereby providing valuable references for future investigations on forecasting system operating conditions.
2. SOFC System Architecture
3. Problem Description and Methodology
3.1. Problem Description
3.2. Methodology
4. Model Building
4.1. BP Neural Network
4.2. Genetic Algorithm
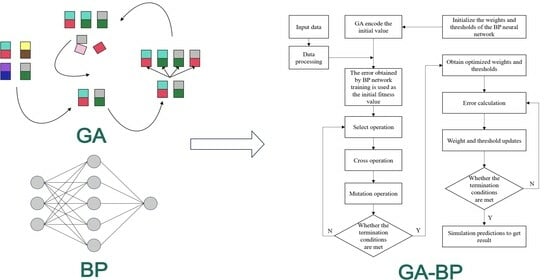
4.3. GA-BP Algorithm Model
- Choice of encoding
- 2.
- Population initialization
- 3.
- Initialize the BP neural network model
- 4.
- Designing the Fitness Function
- 5.
- Selection operation
- 6.
- Cross operation
- 7.
- Mutation operation
- 8.
- Calculate fitness
- 9.
- Termination criterion:
- a.
- Reach the maximum number of iterations.
- b.
- The current best solution has either remained unchanged or changed very little for several consecutive steps.
- c.
- The algorithm has found an acceptable best solution, achieving the performance goal.
- 10.
- Train
5. Model Settings
5.1. Data Sample
5.2. Parameter Settings of BP and GA-BP
6. Results and Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Onn, T.M.; Küngas, R.; Fornasiero, P.; Huang, K.; Gorte, R.J. Atomic Layer Deposition on Porous Materials: Problems with Conventional Approaches to Catalyst and Fuel Cell Electrode Preparation. Inorganics 2018, 6, 34. [Google Scholar] [CrossRef]
- Suchaneck, G.; Artiukh, E. Nonstoichiometric Strontium Ferromolybdate as an Electrode Material for Solid Oxide Fuel Cells. Inorganics 2022, 10, 230. [Google Scholar] [CrossRef]
- Pirou, S.; Talic, B.; Brodersen, K.; Hauch, A.; Frandsen, H.L.; Skafte, T.L.; Persson, A.H.; Hogh, J.V.T.; Henriksen, H.; Navasa, M.; et al. Production of a monolithic fuel cell stack with high power density. Nat. Commun. 2022, 13, 1263. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, K.I.; Ahmed, M.H. Developing a Novel Design for a Tubular Solid Oxide Fuel Cell Current Collector. Appl. Sci. 2022, 12, 6003. [Google Scholar] [CrossRef]
- Pan, Z.; Liu, J.; Liu, J.; Ning, X.; Qin, Z.; He, L. Active Disturbance Rejection Optimization Control for SOFCs in Offshore Wind Power. Appl. Sci. 2023, 13, 3364. [Google Scholar] [CrossRef]
- Wu, X.-L.; Zhang, H.; Liu, H.; Xu, Y.-W.; Peng, J.; Xia, Z.; Wang, Y. Modeling Analysis of SOFC System Oriented to Working Condition Identification. Energies 2022, 15, 1804. [Google Scholar] [CrossRef]
- Zhou, J.; Wang, Z.; Han, M.; Sun, Z.; Sun, K. Optimization of a 30 kW SOFC combined heat and power system with different cycles and hydrocarbon fuels. Int. J. Hydrog. Energy 2022, 47, 4109–4119. [Google Scholar] [CrossRef]
- Marocco, P.; Gandiglio, M.; Santarelli, M. When SOFC-based cogeneration systems become convenient? A cost-optimal analysis. Energy Rep. 2022, 8, 8709–8721. [Google Scholar] [CrossRef]
- Zhou, A.; Li, X.-S.; Ren, X.-D.; Song, J.; Gu, C.-W. Thermodynamic and economic analysis of a supercritical carbon dioxide (S-CO2) recompression cycle with the radial-inflow turbine efficiency prediction. Energy 2020, 191, 116566. [Google Scholar] [CrossRef]
- Yabanova, I.; Kecebas, A. Development of ANN model for geothermal district heating system and a novel PID-based control strategy. Appl. Therm. Eng. 2013, 51, 908–916. [Google Scholar] [CrossRef]
- Jin, F.Y.; Xiong, C.; Zhou, H.F.; Huang, Y.Q. Predictive control simulation of solid oxide fuel cells based on an artificial bee colony-support vector machine (abc-svm) model. J. B. Univ. Chem. Technol. 2021, 48, 96–104. [Google Scholar] [CrossRef]
- Yarullin, D.N.; Zavalishin, M.N.; Gamov, G.A.; Lukanov, M.M.; Ksenofontov, A.A.; Bumagina, N.A.; Antina, E.V. Prediction of Sensor Ability Based on Chemical Formula: Possible Approaches and Pitfalls. Inorganics 2023, 11, 158. [Google Scholar] [CrossRef]
- Al-Nader, I.; Lasebae, A.; Raheem, R.; Khoshkholghi, A. A Novel Scheduling Algorithm for Improved Performance of Multi-Objective Safety-Critical Wireless Sensor Networks Using Long Short-Term Memory. Electronics 2023, 12, 4766. [Google Scholar] [CrossRef]
- Singpai, B.; Wu, D. Using a DEA–AutoML Approach to Track SDG Achievements. Sustainability 2020, 12, 10124. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, N.; Wu, L.; Wang, Y. Wind speed forecasting based on the hybrid ensemble empirical mode decomposition and GA-BP neural network method. Renew. Energy 2016, 94, 629–636. [Google Scholar] [CrossRef]
- Ren, L.; Dong, J.; Wang, X.; Meng, Z.; Zhao, L.; Deen, M.J. A Data-Driven Auto-CNN-LSTM Prediction Model for Lithium-Ion Battery Remaining Useful Life. IEEE Trans. Industr. Inform. 2021, 17, 3478–3487. [Google Scholar] [CrossRef]
- Chen, K.; Laghrouche, S.; Djerdir, A. Aging prognosis model of proton exchange membrane fuel cell in different operating conditions. Int. J. Hydrog. Energy 2020, 45, 11761–11772. [Google Scholar] [CrossRef]
- Huo, H.; Chen, J.; Wang, K.; Wang, F.; Jin, G.; Chen, F. State Estimation of Membrane Water Content of PEMFC Based on GA-BP Neural Network. Sustainability 2023, 15, 9094. [Google Scholar] [CrossRef]
- Petrone, R.; Zheng, Z.; Hissel, D.; Péra, M.C.; Pianese, C.; Sorrentino, M.; Becherif, M.; Yousfi-Steiner, N. A review on model-based diagnosis methodologies for PEMFCs. Int. J. Hydrog. Energy 2013, 38, 7077–7091. [Google Scholar] [CrossRef]
- Li, M.; Chen, Z.; Dong, J.; Xiong, K.; Chen, C.; Rao, M.; Peng, Z.; Li, X.; Peng, J. A Data-Driven Fault Diagnosis Method for Solid Oxide Fuel Cell Systems. Energies 2022, 15, 2556. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, Y.Y.; Hou, G.L.; Fan, P.P.; IEEE. Research on BP algorithm-based SOFC system temperature model. In Proceedings of the 2015 Chinese Automation Congress (CAC), Wuhan, China, 27–29 November 2015; pp. 1932–1935. [Google Scholar] [CrossRef]
- Wu, X.-L.; Xu, Y.-W.; Li, D.; Zheng, Y.; Li, J.; Sorrentino, M.; Yu, Y.; Wan, X.; Hu, L.; Zou, C.; et al. Afterburner temperature safety assessment for solid oxide fuel cell system based on computational fluid dynamics. J. Power Sources 2021, 496, 229837. [Google Scholar] [CrossRef]
- Wu, X.-L.; Xu, Y.-W.; Zhao, D.-Q.; Zhong, X.-B.; Li, D.; Jiang, J.; Deng, Z.; Fu, X.; Li, X. Extended-range electric vehicle-oriented thermoelectric surge control of a solid oxide fuel cell system. Appl. Energy 2020, 263, 114628. [Google Scholar] [CrossRef]
- Cheng, H.; Li, X.; Jiang, J.; Deng, Z.; Yang, J.; Li, J. A nonlinear sliding mode observer for the estimation of temperature distribution in a planar solid oxide fuel cell. Int. J. Hydrog. Energy 2015, 40, 593–606. [Google Scholar] [CrossRef]
- Zhang, L.; Jiang, J.; Cheng, H.; Deng, Z.; Li, X. Control strategy for power management, efficiency-optimization and operating-safety of a 5-kW solid oxide fuel cell system. Electrochim. Acta 2015, 177, 237–249. [Google Scholar] [CrossRef]
- Rao, M.; Wang, L.; Chen, C.; Xiong, K.; Li, M.; Chen, Z.; Dong, J.; Xu, J.; Li, X. Data-Driven State Prediction and Analysis of SOFC System Based on Deep Learning Method. Energies 2022, 15, 3099. [Google Scholar] [CrossRef]
- Oryshchyn, D.; Harun, N.F.; Tucker, D.; Bryden, K.M.; Shadle, L. Fuel utilization effects on system efficiency in solid oxide fuel cell gas turbine hybrid systems. Appl. Energy 2018, 228, 1953–1965. [Google Scholar] [CrossRef]
- Selvam, K.; Komatsu, Y.; Sciazko, A.; Kaneko, S.; Shikazono, N. Thermodynamic analysis of 100% system fuel utilization solid oxide fuel cell (SOFC) system fueled with ammonia. Energy Convers. Manag. 2021, 249, 114839. [Google Scholar] [CrossRef]
- Thai-Quyen, Q.; Van-Tien, G.; Lee, D.K.; Israel, T.P.; Ahn, K.Y. High-efficiency ammonia-fed solid oxide fuel cell systems for distributed power generation. Appl. Energy 2022, 324, 119718. [Google Scholar] [CrossRef]
- Meng, T.; Cui, D.; Ji, Y.L.; Cheng, M.J.; Tu, B.F.; Lan, Z.L. Optimization and efficiency analysis of methanol SOFC-PEMFC hybrid system. Int. J. Hydrog. Energy 2022, 47, 27690–27702. [Google Scholar] [CrossRef]
- Yang, J.; Qin, S.; Zhang, W.Y.; Ding, T.F.; Zhou, B.; Li, X.; Jian, L. Improving the load-following capability of a solid oxide fuel cell system through the use of time delay control. Int. J. Hydrog. Energy 2017, 42, 1221–1236. [Google Scholar] [CrossRef]
- Ruan, X.M.; Zhu, Y.Y.; Li, J.; Cheng, Y. Predicting the citation counts of individual papers via a BP neural network. J. Informetr. 2020, 14, 101039. [Google Scholar] [CrossRef]
- Yang, A.M.; Zhuansun, Y.X.; Liu, C.S.; Li, J.; Zhang, C.Y. Design of Intrusion Detection System for Internet of Things Based on Improved BP Neural Network. IEEE Access 2019, 7, 106043–106052. [Google Scholar] [CrossRef]
- Qu, Z.; Liu, H.; Wang, Z.; Xu, J.; Zhang, P.; Zeng, H. A combined genetic optimization with AdaBoost ensemble model for anomaly detection in buildings electricity consumption. Energy Build. 2021, 248, 111193. [Google Scholar] [CrossRef]
- Kuang, T.; Hu, Z.Y.; Xu, M.H. A Genetic Optimization Algorithm Based on Adaptive Dimensionality Reduction. Math. Probl. Eng. 2020, 2020, 8598543. [Google Scholar] [CrossRef]
- Liu, K.L.; Lin, T.; Zhong, T.T.; Ge, X.R.; Jiang, F.C.; Zhang, X. New methods based on a genetic algorithm back propagation (GABP) neural network and general regression neural network (GRNN) for predicting the occurrence of trihalomethanes in tap water. Sci. Total Environ. 2023, 870, 161976. [Google Scholar] [CrossRef]
- Wentz, V.H.; Maciel, J.N.; Gimenez Ledesma, J.J.; Ando, O.H., Jr. Solar Irradiance Forecasting to Short-Term PV Power: Accuracy Comparison of ANN and LSTM Models. Energies 2022, 15, 2457. [Google Scholar] [CrossRef]










| Hidden Layer Neuron | MSE | Iterations |
|---|---|---|
| 3 | 0.00061 | 20 |
| 5 | 0.00052 | 17 |
| 7 | 0.00074 | 16 |
| 9 | 0.00085 | 15 |
| 11 | 0.00085 | 14 |
| Parameter of BP | Setting |
| Training times | 1000 |
| Neurons in the input layers | 3 |
| Neurons in the hidden layers | 5 |
| Neurons in the output layers | 1 |
| Activation function | tansig |
| Training function | LM |
| Learning rate | 0.1 |
| Training goal | 0.0001 |
| Parameter of GA | Setting |
| Size of the population | 50 |
| Maximum number of evolutions | 50 |
| Crossover probability | 0.8 |
| Mutation probability | 0.05 |
| Generation gap | 0.9 |
| Sample | GA-BP/% | BP/% | LSTM/% | Sample | GA-BP/% | BP/% | LSTM/% |
|---|---|---|---|---|---|---|---|
| 1 | 0.194 | 0.546 | 1.278 | 21 | 0.305 | 0.277 | 0.929 |
| 2 | 0.678 | 0.095 | 1.072 | 22 | 0.389 | 0.678 | 0.595 |
| 3 | 0.141 | 0.043 | 0.196 | 23 | 0.142 | 0.201 | 0.24 |
| 4 | 2.826 | 3.444 | 3.128 | 24 | 0.041 | 0.331 | 0.129 |
| 5 | 1.721 | 0.565 | 1.658 | 25 | 9.724 | 15.068 | 11.053 |
| 6 | 0.461 | 1.652 | 1.431 | 26 | 0.224 | 6.14 | 2.859 |
| 7 | 1.189 | 0.239 | 0.631 | 27 | 1.292 | 0.452 | 0.709 |
| 8 | 0.269 | 0.603 | 1.821 | 28 | 1.998 | 2.248 | 2.049 |
| 9 | 0.622 | 1.553 | 1.246 | 29 | 1.63 | 2.335 | 2.271 |
| 10 | 1.085 | 0.794 | 0.137 | 30 | 0.359 | 0.499 | 0.192 |
| 11 | 0.867 | 2.703 | 0.876 | 31 | 0.353 | 1.247 | 0.323 |
| 12 | 0.884 | 1.669 | 0.983 | 32 | 0.286 | 1.282 | 0.344 |
| 13 | 1.598 | 2.189 | 0.641 | 33 | 0.121 | 0.505 | 0.108 |
| 14 | 0.75 | 0.095 | 1.57 | 34 | 0.737 | 1.164 | 1.839 |
| 15 | 0.439 | 0.184 | 1.186 | 35 | 0.517 | 1.443 | 1.438 |
| 16 | 0.578 | 0.488 | 0.14 | 36 | 0.021 | 1.385 | 1.09 |
| 17 | 1.052 | 1.523 | 0.837 | 37 | 0.345 | 0.276 | 0.522 |
| 18 | 2.822 | 4.207 | 2.801 | 38 | 0.035 | 1.575 | 2.027 |
| 19 | 1.476 | 1.556 | 1.903 | 39 | 0.282 | 2.45 | 2.286 |
| 20 | 1.345 | 2.09 | 2.445 | 40 | 0.213 | 2.175 | 1.517 |
| Parameter | Setting |
|---|---|
| Batch size | 30 |
| Neurons in the input layers | 3 |
| Number of hidden layers | 1 |
| Neurons in the hidden layers | 16 |
| Neurons in the output layers | 1 |
| Learning rate | 0.01 |
| Training times | 1000 |
| Optimizer | Adam |
| MSE | R2 | Maximum Error | Minimum Error | Average Error | Training Duration | |
|---|---|---|---|---|---|---|
| BP | 92.67 | 0.9573 | 15.068% | 0.043% | 1.7% | 4 s |
| GA-BP | 35.94 | 0.9832 | 9.724% | 0.021% | 1% | 83 s |
| LSTM | 56.50 | 0.9733 | 11.053% | 0.108% | 1.5% | 61 s |
| MSE | R2 | Maximum Error | Minimum Error | Average Error | |
|---|---|---|---|---|---|
| GA-BP | 43.82 | 0.9805 | 4.325% | 0.032% | 1.3% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, D.; Hu, J.; Zhao, W.; Lai, M.; Gao, Z.; Wu, X. A Single-Stack Output Power Prediction Method for High-Power, Multi-Stack SOFC System Requirements. Inorganics 2023, 11, 474. https://doi.org/10.3390/inorganics11120474
Zhang D, Hu J, Zhao W, Lai M, Gao Z, Wu X. A Single-Stack Output Power Prediction Method for High-Power, Multi-Stack SOFC System Requirements. Inorganics. 2023; 11(12):474. https://doi.org/10.3390/inorganics11120474
Chicago/Turabian StyleZhang, Daihui, Jiangong Hu, Wei Zhao, Meilin Lai, Zilin Gao, and Xiaolong Wu. 2023. "A Single-Stack Output Power Prediction Method for High-Power, Multi-Stack SOFC System Requirements" Inorganics 11, no. 12: 474. https://doi.org/10.3390/inorganics11120474
APA StyleZhang, D., Hu, J., Zhao, W., Lai, M., Gao, Z., & Wu, X. (2023). A Single-Stack Output Power Prediction Method for High-Power, Multi-Stack SOFC System Requirements. Inorganics, 11(12), 474. https://doi.org/10.3390/inorganics11120474