A Comparison of β–Phenyl Elimination in Nickel and Palladium Alkyl Complexes: A Potentially Relevant Process in the Mizoroki–Heck Reaction

Abstract

There is currently much interest in avoiding precious metals in catalysis. The development of nickel catalysts to replace palladium in the Mizoroki–Heck reaction is a relevant case in this line of research, since both elements share many chemical features. This contribution focuses on β–phenyl (β–Ph) elimination in alkyl—nickel complexes. This is the microscopic reverse of olefin insertion (or carbometallation), a fundamental step in the Heck cycle that is usually considered irreversible and selectivity-determining. However, the potential reversibility of carbometallation is generally concealed by the facile β–hydrogen (β–H) elimination that follows. Where β–hydrogen elimination is hindered, β–aryl elimination may ensue. We have previously shown that cationic 2–methyl–2–phenylpropyl (neophyl) palladium complexes supported by bidentate ligands experience β–Ph elimination, which can be seen as an example of olefin de-insertion. In this contribution, we report that β–Ph elimination can also occur in their nickel analogs, in which case fast hydrolyses of the resulting phenyl product can follow the reaction. We investigated the mechanism of these processes and compared their feasibility for nickel and palladium catalysts using DFT calculations. These results are relevant information for the design of nickel-based catalysts for the Heck reaction.

1. Introduction

Olefin insertion into metal–carbon bonds, or olefin carbometallation, is a fundamental process responsible for C–C bond formation in valuable catalytic processes [1], such as olefin polymerization [2,3,4,5,6,7,8,9,10,11,12] and oligomerization [13,14,15,16,17,18,19], or the Mizoroki–Heck reaction [20,21]. In most cases, this involves a migratory insertion route. This mechanistic category implies the pre-coordination of the olefin molecule to the metal center, followed by the attack by a pre-existing σ bonded ligand (Scheme 1) [1]. The reversal of olefin insertion into a metal–carbon bond is called β–carbon (β–C) elimination. Although the microscopic reversibility principle [22] dictates that the latter should also occur, this is much more rarely observed [23].

In contrast, β–hydrogen (β–H) elimination, the reverse of olefin insertion into metal–hydride bonds (hydrometallation), is ubiquitous. In part, the difference stems from thermodynamic reasons. Usually, β–C elimination is endothermic since the formation of an olefin π–bond does not compensate for the cleavage of a strong σ C–C bond [24]. In contrast, for β–H elimination, the strength of the M–H bond compensates for this unfavorable factor, leading to a nearly thermoneutral balance on a general basis. The literature collects many examples of reversible β–H elimination [5,25,26,27,28,29,30]. Kinetic reasons also play a critical part in the scarcity of β–C eliminations: there are usually more C–H bonds in β positions, which are much more readily accessible for the metal than β–C–C bonds. In addition, the interaction of the metal with a C–C bond implies the reorganization of highly directional atomic p orbitals of carbon, in contrast with the non-directional s orbital of the hydrogen atom [31].

In the Mizoroki–Heck reaction, olefin insertion produces organic fragments with one or more C–H bonds. Therefore, the potential reversibility of the olefin insertion reaction is usually masked by competitive β–H elimination. The prevalence of β–H over β–C eliminations is an essential feature of the Mizoroki–Heck reaction, where olefin carbometallation is followed by fast β–H elimination.

Despite the above considerations, β–C elimination is an accessible mechanistic avenue that emerges as a dominant process in some situations. For instance, β–methyl elimination constitutes a frequent termination mechanism in propene polymerization by early transition metals, for which the process becomes exergonic due to the increased strength of the resulting M–Me bond [32]. Very recently, a Hf(IV) metallocene/MAO catalyst has even been shown to depolymerize polypropylene, which implicitly involves the ability to revert the propene enchainment reaction via β–alkyl elimination recursively [33]. Although the thermodynamic preference of transition metals for β–hydrogen over β–carbon elimination increases as the metal center becomes electron-richer along the transition rows [22], alkyl–metal complexes of palladium and platinum experience β–carbon elimination if favorable conditions are met. For instance, β–C prevails over β–H eliminations if it involves strained, reactive C–C bonds, such as those in cyclopropane or cyclobutane, or when a rigid configuration of the alkyl ligand prevents C–H bonds in the β–position to attain a coplanar arrangement with the metal fragment, as required to enable β–H elimination [34]. Reversible olefin insertion is involved in the Catellani reaction (palladium–norbornene cooperative catalysis), in which norbornene insertion and de-insertion into Pd–aryl bonds enables the functionalization of the aryl ring on both ortho positions via cascade-type insertion–cyclometallation–alkylation reactions [35]. Interestingly, Amatore and Jutand proposed that reversible olefin insertions may play a role in the regioselectivity control of the Mizoroki–Heck reaction of electron-rich olefins under cationic conditions when cationic Pd/diphosphine complexes catalyze the arylation [36]. This implies that, in such cases, the energy barriers for β–phenyl (β–Ph) and β–H eliminations are comparable.

Years ago, our group [37] and others [38] reported that alkyl ligands with a β–phenyl group can stabilize formally unsaturated 14-electron Pd species such as 1 owing to their ability to donate π–electrons to the electron-deficient metal center (Scheme 2). In this work, we used the neophyl group (i.e., 2–methyl–2–phenylpropyl), as a privileged platform for investigating β–Ph elimination. This alkyl group contains no β–H atoms, featuring only methyl and phenyl substituents, and any β–carbon elimination occurs without raising the reactivity of the C–C bonds with ring strain. Depending on the spectator co-ligands, such π–arene interactions serve as precursors for various reactions, mainly o–metallation or β–Ph elimination. Specifically, whereas monodentate PMe₃ ligands favor o–phenyl palladation [37], the electronically similar but chelating diphosphine 1,2–bis(dimethylphosphino)ethane (DMPE) selectively induces β–Ph elimination (Scheme 2) [39]. To stabilize the Pd(II)–Ph product as the PMe₃ adduct 2, the coordinatively saturated neophyl complex [Pd(CH₂CMe₂Ph)(PMe₃)(DMPE)]⁺ [BAr’₄]⁻ (3, Ar’ = 3,5–bistrifluoromethylphenyl) is used as a PMe₃ source. Compound 3 is not reactive by itself: it requires the presence of 1, which is responsible for the β–Ph elimination process. Such reaction sequence ultimately leads to a 1-catalyzed conversion of 3 into 2, concurrent with isobutene elimination. The resistance of the saturated, 16-electron complex 3 to β–Ph elimination stands in contrast with the ability of palladium alkyl complexes susceptible to the β–H elimination process, which is known to proceed even from either 14- or 16-electron alkyl intermediates [39]. The latter involves a pentacoordinate transition state for the hydrogen abstraction, in accordance with early computational work by Thorn and Hoffmann [40]. As commented above, the reluctance of palladium alkyls to undergo β–carbon through pentacoordinate intermediates contrasts with their ability for β–H elimination. This feature is paramount for the efficiency and selectivity of the Mizoroki–Heck reaction.

In this contribution, we report on the ability of cationic neophyl Ni(II) species akin to the above Pd(II) complexes to undergo β–Ph elimination. We provide evidence for β–Ph elimination from Ni(II) complexes under mild conditions for the first time. Whereas β–C elimination reactions are not alien to Ni(II) chemistry [41,42], to our knowledge, this has never been noted for non-strained complexes. Surprisingly, Ni(II) phenyl complexes arising from the isobutene de-insertion are exceedingly prone to hydrolysis, being converted into binuclear hydroxides by the moisture traces in reagents, solvents, and equipment.

Due to the potential importance that the reversibility of olefin insertion may have for the applications of Ni as a more sustainable replacement for Pd in homogeneous catalysis, we complete this study with a comparative computational analysis of β–Ph elimination in 14- and 16-electron complexes of Ni(II) and Pd(II). Our studies include the final hydrolyses step, as this could represent an essential difference in the stability of both types of catalysts.

2. Materials and Methods

General Considerations. All experiments were carried out under dry nitrogen using standard Schlenk techniques. Solvents were rigorously dried and degassed before use. Microanalyses were performed by Pascher Microanalytical Laboratory (Remagen, Germany) and the Microanalytical Service of the University of Seville and Instituto de Investigaciones Químicas (Seville, Spain). Infrared spectra were recorded in Nujol mulls on Perkin-Elmer FT-16PC (Shelton, CT, USA) and Bruker Vector 22 spectrometers (Bruker Optics, Ettligen, Germany)) while NMR spectra were obtained on Bruker AMX-300, AMX-500, DRX-400, and DRX-500 spectrometers (Bruker AXS, Karlsruhe, Germany). ³¹P{¹H} NMR resonances are referenced to 85% H₃PO₄ as an external standard. The residual ¹H and ¹³C{¹H} resonances of the solvents were used as internal standards, but the chemical shifts were reported relative to TMS. Chemical shifts (δ) are given in ppm, and coupling constants (J) are given in Hz. Abbreviations for multiplicities are as follows: br, broad; s, singlet; d, doublet; t, triplet; c, quartet; q, quintet; sp, septet; m, multiplet; v, virtual; dvt, doublet of virtual triplet; pt, pseudo triplet. Compounds 4a,b [43], [Ni(Me)₂DiPP]) [43], and [HPMe₃][BAr’₄] [39] were prepared as reported previously. Pyridinium triflate was prepared as a white precipitate by mixing equimolar amounts of triflic acid and pyridine in diethyl ether, which was filtered and dried under vacuum.

[Ni(OH)DiPPE]₂[TfO]₂, 5a, and [Ni(OH)DiPPP]₂[TfO]₂, 5b. 0.78 mL of a 0.64 M solution of HTfO (0.5 mmol) in Et₂O was added to a stirred solution of complex 4a (226 mg, 0.5 mmol) in 30 mL of Et₂O at −80 °C. The resulting yellow suspension was allowed to reach room temperature and then stirred at room temperature for one hour. The suspension turned to a red-orange color. This was evaporated to dryness, and the residue was extracted with 20 mL of CH₂Cl₂. The solution was filtered and concentrated under reduced pressure, and some toluene was added. Compound 5a was obtained as red crystals after cooling the solution in the freezer at −30 °C. (Yield: 88%.) Anal. Calcd. for C₃₀H₆₆F₆Ni₂O₈P₄S₂.0.5 C₇H₈: C, 39.44; H, 6.92. Found: C, 38.90; H, 7.14. IR (Nujol mull): ν(O–H) 3594 cm⁻¹. ¹H NMR (400 MHz, CD₂Cl₂, 25 °C): δ −1.51 (q, 1H, J_HP = 1.9 Hz, OH), 1.25 (dd, 12H, ³J_HP = 13.9 Hz, ³J_HH = 7.0 Hz, CH₃), 1.56 (d, 4H, J_HP = 11.3 Hz, CH₂), 1.67 (dd, 12H, ³J_HP = 17.9 Hz, ³J_HH = 7.0 Hz, CH₃), 2.38 (m, 4H, CH). ¹³C{¹H} NMR (100.6 MHz, CD₂Cl₂, 25 °C): δ 19.6 (s, 4C, CH₃), 20.0 (t, 2C, J*_CP = 20.0 Hz, CH₂), 22.3 (s, 4C, CH₃), 26.3 (t, 4C, J*_CP = 12.0 Hz, CH), 122.5 (c, 2C, ¹J_CF = 321.0 Hz, CF₃). ³¹P{¹H} NMR (162 MHz, CD₂Cl₂, 25 °C) δ 88.0 (s).

Compound 5b was prepared using the same procedure. (Yield: 85%.) Anal. Calcd. for C₃₂H₇₀F₆Ni₂O₈P₄S₂: C, 38.35; H, 7.04. Found: C, 38.37; H, 6.92. IR (Nujol mull): ν(O–H) 3513 cm⁻¹. ¹H NMR (400 MHz, CD₂Cl₂, 25 °C): δ −3.27 (s, 1H, OH), 1.30 (m, 16H, CH₃, CH₂) 1.70 (dd, 12H, ³J_HP = 17.5 Hz, ³J_HH = 8.0 Hz, CH₃), 1.83 (m, 2H, CH₂), 2.01 (m, 4H, CH). ¹³C{¹H} NMR (100.6 MHz, CD₂Cl₂, 25 °C) δ 14.7 (t, 2C, J*_CP = 16.0 Hz, CH₂), 17.7 (s, 4C, CH₃), 20.7 (s, 1C, CH₂), 20.8 (s, 4C, CH₃), 25.2 (t, 4C, J*_CP = 12.0 Hz, CH). ³¹P{¹H} NMR (162 MHz, CD₂Cl₂, 25 °C) δ 27.4 (s).

Ni(CH₂CMe₂Ph)(TfO)(DiPPE), 6a, and Ni(CH₂CMe₂Ph)(TfO)(DiPPP), 6b. A solution of the complex 4a (220 mg, 0.44 mmol) in 50 mL of Et₂O and cooled to −75 °C was treated with 0.73 mL (0.44 mmol) of a 0.6 M solution of HTfO in Et₂O. The mixture was stirred for 15 min at this temperature, and a yellow precipitate was formed. The suspension was filtered, and the solid residue was dried under vacuum. ¹H NMR (400 MHz, CD₂Cl₂, 25 °C): δ 0.78 (dd, 2H, ³J_HP = 4.8, 14.0 Hz, Ni–CH₂), 1.35 (m, 16H, CH₃, CH₂ DiPPE), 1.40 (s, 6H, CMe₂), 1.45 (m, 12H, CH₃ DiPPE), 2.26 (m, 2H, CH DiPPE), 2.39 (m, 2H, CH DiPPE), 7.56 (t, 1H, ³J_HH = 6.6 Hz, p–CH_ar), 7.82 (t, 2H, ³J_HH = 6.3 Hz, m–CH_ar), 8.00 (d, 2H, ³J_HH = 7.0 Hz, o–CH_ar). ³¹P{¹H} (162 MHz, CD₂Cl₂, 25 °C) AX spin system: δ_A = 57.0, δ_X = 69.2, ²J_AX = 9.3 Hz.

6b: Applying the same procedure to 4b led to a yellow precipitate, which was similarly collected, and its ¹H and ³¹P{¹H} spectra were recorded in CD₂Cl₂. The sample was impurified with 5b. Therefore, only selected signals are provided. ¹H NMR (400 MHz, CD₂Cl₂, 25 °C): δ 1.2–1.5 (DiPPP ligand and Ni–CH₂, overlapping signals), 1.56 (s, 6H, CMe₂), 1.72 2.26 (m, 2H, CH DiPPP), 7.20 (t, 1H, ³J_HH = 6.6 Hz, p–CH_ar), 7.34 (t, 2H, ³J_HH = 6.4 Hz, m–CH_ar), 7.53 (d, 2H, ³J_HH = 6.0 Hz, o–CH_ar). ³¹P{¹H} (162 MHz, CD₂Cl₂, 25 °C) AX spin system: δ_A = 10.3, δ_X = 30.7 (broad), ²J_AX = 29.3 Hz.

[Ni(CH₂CMe₂Ph)(py)DiPPE][TfO], 7a, and [Ni(Ph)(py)DiPPE][TfO], 8a. A sample of 240 mg (0.5 mmol) of complex 4a was dissolved in 30 mL of Et₂O, the solution was cooled to −60 °C, and a suspension of 125 mg (0.5 mmol) of pyridinium triflate in 20 mL of Et₂O was added. The mixture was stirred at −20 °C for two hours, forming a yellow solid. The suspension was filtered, and the solid residue dried under a vacuum. A sample was dissolved in CD₂Cl₂, and NMR spectra were recorded immediately and 24 h later. The former shows mainly signals of 7a and the latter of 8a. Data for 7a: ¹H (400 MHz, CD₂Cl₂, 25 °C): δ 0.85 (dd, 6H, ³J_HP = 15.0 Hz, ³J_HH = 7.5 Hz, CH₃ DiPPE), 1.05 (dd, 6H, ³J_HP = 12.7 Hz, ³J_HH = 6.9 Hz, CH₃ DiPPE), 1.25 (s, 6H, CMe₂), 1.38 (dd, 6H, ³J_HP = 13.7 Hz, ³J_HH = 6.9 Hz, CH₃ DiPPE), 1.51 (dd, 6H, ³J_HP = 15.5 Hz, ³J_HH = 7.5 Hz, CH₃ DiPPE), 1.59 (dd, 2H, ³J_HP = 3.0, 8.0 Hz, Ni–CH₂), 1.65 (m, 2H, CH₂ DiPPE), 1.84 (m, 4H, CH₂, CH DiPPE), 2.39 (sp, 2H, ³J_HH = 7.0 Hz, CH DiPPE), 6.93 (t, 1H, ³J_HH = 7.4 Hz, p–CH_ar Ph), 6.99 (t, 2H, ³J_HH = 7.4 Hz, m–CH_ar Ph), 7.12 (t, 2H, ³J_HH = 6.3 Hz, 3–CH_ar py), 7.56 (t, 1H, ³J_HH = 7.2 Hz, 4–CH_ar py), 8.0 (d, 2H, ³J_HH = 5.7 Hz, o–CH_ar Ph), 8.41 (d, 2H, ³J_HH = 5.0 Hz, 2–CH_ar py). ³¹P{¹H} (162 MHz, CD₂Cl₂, 25 °C) δ 59.2, 72.4 (s). Data for 8a: δ 1.0–1.3 (overlapping signals, 12H, CH₃ DiPPE); 1.7–1.4 (overlapping signals, 8H, 2 CH₂ + CH DiPPE), 2.31 (sp, 2H, ³J_HH = 7.0 Hz, CH DiPPE), 6.82 (t, 1H, ³J_HH = 7.4 Hz, p–CH_ar Ph), 6.91 (t, 2H, ³J_HH = 7.4 Hz, m–CH_ar Ph), 7.4–7.6 (overlapping multiplets, 4H, 3–CH_ar py and o–CH Ph); 7.72 (t, 1H, ³J_HH = 7.2 Hz, 4–CH_ar py), 8.75 (d, 2H, ³J_HH = 5.0 Hz, 2–CH_ar py). ³¹P{¹H} (162 MHz, CD₂Cl₂, 25 °C): AX spin system: δ_A = 65.1, δ_X = 72.1, ²J_AX = 11.4 Hz.

[Ni(CH₂CMe₂Ph)(DMAP)DiPPE][TfO], 9a. To a solution of complex 4a (110 mg, 0.24 mmol) in 20 mL of Et₂O, cooled to −70 °C, pyridinium triflate (55.6 mg, 0.24 mmol) was added, suspended in 25 mL of Et₂O. The mixture was stirred for 15 min at this temperature and then held for 30 min at −20 °C. Then, DMAP (30 mg, 0.24 mmol) was added, and the resulting suspension was stirred at room temperature for two hours. The suspension was filtered, and the yellow solid residue was washed with Et₂O (2 × 10 mL) and dried under vacuum. (Yield: 88%.) ¹H (400 MHz, (CD₃)₂CO, 25 °C): δ 0.99 (dd, 6H, ³J_HP = 15.0 Hz, ³J_HH = 7.3 Hz, CH₃ DiPPE), 1.12 (dd, 6H, ³J_HP = 13.0 Hz, ³J_HH = 7.0 Hz, CH₃ DiPPE), 1.28 (s, 6H, CMe₂), 1.36 (dd, 6H, ³J_HP = 13.4 Hz, ³J_HH = 7.0 Hz, CH₃ DiPPE), 1.49 (dd, 6H, ³J_HP = 15.5 Hz, ³J_HH = 7.3 Hz, CH₃ DiPPE), 1.58 (dd, 2H, ³J_HP = 3.8, 9.0 Hz, Ni–CH₂), 1.75 (m, 2H, CH₂ DiPPE), 2.0 (m, 4H, CH₂, CH DiPPE), 2.42 (m, 2H, CH DiPPE), 3.0 (s, 6H, NMe₂ DMAP), 6.45 (d, 2H, ³J_HH = 7.3 Hz, DMAP), 6.91 (t, 1H, ³J_HH = 7.3 Hz, p–CH_ar Ph), 7.01 (t, 2H, ³J_HH = 8.0 Hz, m–CH_ar Ph), 7.17 (d, 2H, ³J_HH = 7.2 Hz, o–CH_ar Ph), 8.07 (d, 2H, ³J_HH = 7.5 Hz, DMAP). ¹³C{¹H} (100.6 MHz, (CD₃)₂CO, 25 °C): δ 18.4 (s, 2C, CH₃ DiPPE), 18.5 (m, 1C, CH₂ DiPPE), 18.7 (d, 2C, ²J_CP = 2.0 Hz, CH₃ DiPPE), 19.1 (d, 2C, ²J_CP = 5.0 Hz, CH₃ DiPPE), 20.8 (d, 2C, ²J_CP = 2.0 Hz, CH₃ DiPPE), 23.1 (dd, ²J_CP = 20.0, 26.0 Hz, Ni–CH₂), 24.7 (d, 2C, ¹J_CP = 15.0 Hz, CH DiPPE), 26.1 (d, 2C, ¹J_CP = 26.0 Hz, CH DiPPE), 34.3 (d, ⁴J_CP = 5.0 Hz, CMe₂), 39.1 (s, 2C, NMe₂ DMAP), 41.6 (s, CMe₂), 108.9 (s, 2C, C_arH, DMAP), 125.0 (s, 1C, p–C_arH Ph), 126.3 (s, 2C, C_arH Ph), 128.4 (s, 2C, C_arH Ph), 150.3 (s, 2C, C_arH, DMAP), 154.0 (s, 1C, C_ar, DMAP), 155.4 (s, 1C, i–C_ar Ph). ³¹P{¹H} (162 MHz, (CD₃)₂CO, 25 °C): δ 60.6, 73.0 (s).

[Ni(Me)(py)(DiPPE)][TfO], 10a. A solution containing 100 mg (0.28 mmol) of the dimethyl precursor [NiMe₂(DiPPE)] in 20 mL of Et₂O and cooled to −65 °C was treated with a suspension of pyridinium triflate (44 mg, 0.28 mmol) in 20 mL of Et₂O. The mixture was stirred for 15 min at this temperature and then held for 4 h at 0 °C. A yellow solid was formed. The suspension was filtered, and the solid was washed with Et₂O (2 × 10 mL) and dried under vacuum. (Yield: 92%.) ¹H (400 MHz, CD₂Cl₂, 25 °C): δ −0.07 (dd, 6H, ³J_HP = 5.0 Hz, Ni–CH₃), 0.98 (dd, 6H, ³J_HP = 15.2 Hz, ³J_HH = 7.2 Hz, CH₃ DiPPE), 1.19 (dd, 6H, ³J_HP = 13.4 Hz, ³J_HH = 6.9 Hz, CH₃ DiPPE), 1.34 (dd, 6H, ³J_HP = 14.2 Hz, ³J_HH = 7.1 Hz, CH₃ DiPPE), 1.40 (dd, 6H, ³J_HP = 16.5 Hz, ³J_HH = 7.2 Hz, CH₃ DiPPE), 1.71 (m, 2H, CH₂ DiPPE), 1.91 (m, 2H, CH₂ DiPPE), 2.01 (m, 2H, CH DiPPE), 2.33 (m, 2H, CH DiPPE), 7.59 (t, 2H, ³J_HH = 6.6 Hz, 3–CH_ar py), 7.91 (t, 1H, ³J_HH = 7.3 Hz, 4–CH_ar py), 8.71 (d, 2H, ³J_HH = 4.4 Hz, 2–CH_ar py). ¹³C{¹H} (100.6 MHz, CD₂Cl₂, 25 °C): δ 4.2 (dd, 1C, ²J_CP = 35.0, 59.0 Hz, Ni–CH₃), 17.8 (dd, 1C, ¹J_CP = 24.0 Hz, ²J_CP = 10.0 Hz, CH₂ DiPPE), 18.5 (s, 2C, CH₃ DiPPE), 18.8 (s, 2C, CH₃ DiPPE), 19.1 (s, 2C, CH₃ DiPPE), 20.5 (s, 2C, CH₃ DiPPE), 23.3 (dd, 1C, ¹J_CP = 23.0 Hz, ²J_CP = 20.0 Hz, CH₂ DiPPE), 24.1 (d, 2C, ¹J_CP = 17.0 Hz, CH DiPPE), 26.3 (d, 2C, ¹J_CP = 29.0 Hz, CH DiPPE), 126.7 (s, 2C, C_arH py), 138.6 (s, 1C, C_arH py), 150.1 (s, 2C, C_arH py). ³¹P{¹H} (162 MHz, CD₂Cl₂, 25 °C): δ 64.3, 81.6 (d, ²J_PP = 4.8 Hz).

[Ni(Me)(DMAP)(DiPPE)][TfO] 11a. A sample of 110 mg (0.31 mmol) of the dimethyl precursor [NiMe₂(DiPPE)] was dissolved in 20 mL of Et₂O, the solution was cooled to −70 °C, and a suspension of 70 mg (0.31 mmol) of pyridinium triflate in 20 mL of Et₂O was added. The mixture was stirred for 15 min at this temperature and then held for one hour at 0 °C, and a solution of 38 mg (0.31 mmol) de DMAP in 10 mL of Et₂O was added. The resulting suspension was stirred at room temperature for four hours, filtered, and the yellow residue washed with Et₂O (2 × 10 mL) and dissolved in a mixture of acetone/hexane. After cooling the solution to −30 °C overnight, compound 11a was isolated as yellow crystals. (Yield: 87%.) Anal. Calcd. for C₂₃H₄₅F₃N₂NiO₃P₂S: C, 45.49; H, 7.47. Found: C, 44.64; H, 6.64. ¹H (400 MHz, (CD₃)₂CO, 25 °C): δ −0.14 (dd, 3H, ³J_HP = 4.0, 5.3 Hz, Ni–CH₃), 1.07 (dd, 6H, ³J_HP = 15.0 Hz, ³J_HH = 7.3 Hz, CH₃ DiPPE), 1.23 (dd, 6H, ³J_HP = 13.3 Hz, ³J_HH = 7.0 Hz, CH₃ DiPPE), 1.34 (dd, 6H, ³J_HP = 14.0 Hz, ³J_HH = 7.0 Hz, CH₃ DiPPE), 1.39 (dd, 6H, ³J_HP = 16.2 Hz, ³J_HH = 7.3 Hz, CH₃ DiPPE), 1.80 (m, 2H, CH₂ DiPPE), 2.0 (m, 4H, CH₂, CH DiPPE), 2.40 (m, 2H, CH DiPPE), 3.1 (s, 6H, NMe₂ DMAP), 6.85 (d, 2H, ³J_HH = 7.0 Hz, CH_ar DMAP), 8.30 (d, 2H, ³J_HH = 6.1 Hz, CH_ar DMAP). ¹³C{¹H} (100.6 MHz, (CD₃)₂CO, 25 °C): δ 3.3 (dd, 1C, ²J_CP = 35.0, 63.0 Hz, Ni–CH₃), 18.0 (dd, 1C, ¹J_CP = 24.0 Hz, ²J_CP = 10.0 Hz, CH₂ DiPPE), 18.6 (s, 2C, CH₃ DiPPE), 18.9 (s, 2C, CH₃ DiPPE), 19.2 (d, 2C, ²J_CP = 4.0 Hz, CH₃ DiPPE), 20.5 (s, 2C, CH₃ DiPPE), 23.6 (dd, 1C, ¹J_CP = 24.0 Hz, ²J_CP = 20.0 Hz, CH₂ DiPPE), 24.5 (d, 2C, ¹J_CP = 17.0 Hz, CH DiPPE), 26.4 (d, 2C, ¹J_CP = 29.0 Hz, CH DiPPE), 39.2 (s, 2C Me DMAP), 109.4 (s, 2C, C_arH DMAP), 149.7 (s, 2C, C_arH DMAP), 155.4 (s, 1C, C_ar DMAP). ³¹P{¹H} (162 MHz, (CD₃)₂CO, 25 °C): δ 65.3, 81.7 (d, ²J_PP = 5.0 Hz).

Synthesis of [Ni(Me)(DMAP)(DiPPP)][TfO], 11b. To a solution of 130 mg (0.31 mmol) of complex 53b in 20 mL of Et₂O cooled to −70 °C, pyridinium triflate (73 mg, 0.31 mmol) suspended in 20 mL of Et₂O was added. The mixture was stirred at this temperature for 15 min and then held for two hours at −20 °C, and a solution of 39 mg (0.31 mmol) of DMAP dissolved in 10 mL of Et₂O was added. The resulting suspension was stirred at room temperature for two hours, filtered, and the yellow residue washed with Et₂O (2 × 10 mL) and dried under vacuum. (Yield: 87%.) ¹H (400 MHz, (CD₃)₂CO, 25 °C): δ −0.18 (pt, 3H, ^*J_HP = 4.3 Hz, Ni–CH₃), 1.20 (dd, 12H, CH₃ DiPPP), 1.33 (dd, 6H, ³J_HP = 13.0 Hz, ³J_HH = 6.9 Hz, CH₃ DiPPP), 1.43 (m, 2H, CH₂ DiPPP), 1.54 (dd, 6H, ³J_HP = 17.0 Hz, ³J_HH = 7.4 Hz, CH₃ DiPPP), 1.63 (m, 2H, CH₂ DiPPP), 1.93 (m, 4H, CH₂, CH DiPPP), 2.31 (m, 2H CH DiPPP), 3.10 (s, 6H, NMe₂ DMAP), 6.85 (d, 2H, ³J_HH = 5.9 Hz, CH_ar DMAP), 8.34 (d, 2H, ³J_HH = 5.9 Hz, CH_ar DMAP). ¹³C{¹H} (100.6 MHz, (CD₃)₂CO, 25 °C): δ 5.9 (dd, 1C, ²J_CP = 38.0, 59.0 Hz, Ni–CH₃), 17.5 (dd, 1C, ¹J_CP = 18.0 Hz, ²J_CP = 10.0 Hz, CH₂ DiPPP), 18.0 (s, 2C, CH₃ DiPPP), 18.7 (t, 1C, ¹J_CP = 18.0 Hz, CH₂ DiPPP), 18.9 (s, 2C, CH₃ DiPPP), 19.7 (s, 2C, CH₃ DiPPP), 21.7 (t, 1C, ¹J_CP = 18.0 Hz, CH₂ DiPPP), 22.3 (s, 2C, CH₃ DiPPP), 25.3 (t, 1C, ¹J_CP = 18.0 Hz, CH DiPPP), 27.4 (t, 1C, ¹J_CP = 31.0 Hz, CH₂ DiPPP), 39.2 (s, 2C Me DMAP), 109.5 (s, 2C, C_arH DMAP), 149.9 (s, 2C, C_arH DMAP), 155.4 (s, 1C, C_ar DMAP). ³¹P{¹H} (162 MHz, (CD₃)₂CO, 25 °C): δ 7.1, 34.8 (d, ²J_PP = 37.0 Hz).

[Ni(Ph)(PMe₃)DiPPE][BAr’₄], 12. A solution of complex 58a (113 mg, 0.25 mmol) in 30 mL of Et₂O cooled to −70 °C was treated with 232 mg (0.25 mmol) of [HPMe₃][BAr’₄], and the resulting mixture was allowed to reach room temperature and stirred at this temperature for three hours. The mixture was evaporated to dryness, and the residue was extracted with 20 mL of Et₂O. The solution was filtered, and some hexane was added. Compound 12 was isolated as yellow crystals after cooling the solution to −30 °C overnight. (Yield: 86%.) Anal. Calcd. for C₅₅H₅₈B F₂₄NiP₃: C, 49.39; H, 4.37. Found: C, 49.35; H, 3.98. ¹H (400 MHz, CD₂Cl₂, 25 °C): δ 0.97 (dd, 6H, ³J_HP = 15.8 Hz, ³J_HH = 7.7 Hz, CH₃ DiPPE), 1.08 (dd, 6H, ³J_HP = 12.9 Hz, ³J_HH = 7.2 Hz, CH₃ DiPPE), 1.14 (d, 9H, ²J_HP = 8.0 Hz, PMe₃), 1.30 (dd, 6H, ³J_HP = 14.0 Hz, ³J_HH = 6.6 Hz, CH₃ DiPPE), 1.34 (dd, 6H, ³J_HP = 17.5 Hz, ³J_HH = 6.7 Hz, CH₃ DiPPE), 1.88 (m, 4H, CH₂ DiPPE), 2.17 (m, 4H, CH DiPPE), 6.99 (t, 1H, ³J_HH = 6.6 Hz, p–CH_ar Ph), 7.14 (t, 2H, ³J_HH = 7.1 Hz, m–CH_ar Ph), 7.27 (m, 2H, o–CH_ar Ph), 7.61 (s, 4H, CH_ar BAr’₄), 7.77 (s, 8H, CH_ar BAr’₄). ¹³C{¹H} (100.6 MHz, CD₂Cl₂, 25 °C): δ 15.3 (d, 3C, ¹J_CP = 30 Hz, PMe₃), 17.5 (s, 2C, CH₃ DiPPE), 18.8 (d, 2C, ²J_CP = 3.0 Hz, CH₃ DiPPE), 19.1 (m, 1C, CH₂ DiPPE), 19.5 (s, 2C, CH₃ DiPPE), 21.3 (pt, 1C, ^*J_CP = 18 Hz, CH₂ DiPPE), 21.6 (d, 2C, ²J_CP = 6.0 Hz, CH₃ DiPPE), 25.0 (d, 2C, ¹J_CP = 26 Hz, CH DiPPE), 26.5 (d, 2C, ¹J_CP = 19 Hz, CH DiPPE), 117.8 (s, 4C, C_arH BAr’₄), 124.4 (s, 1C, C_arH Ph), 124.9 (c, 8C, ¹J_CF = 272 Hz, CF₃ BAr’₄), 128.2 (s, 2C, C_arH Ph), 129.2 (c, 8C, ²J_CF = 32 Hz, C_arCF₃ BAr’₄), 135.1 (s, 8C, C_arH BAr’₄), 137.0 (s, 2C, C_arH Ph), 150.0 (m, 1C, C_ar Ph), 162.1 (c, 4C, ¹J_CB = 46 Hz, CB BAr’₄). ³¹P{¹H} (162 MHz, CD₂Cl₂, 25 °C): δ 18.8 (dd, ²J_PP = 30, 243 Hz), 68.9 (dd, ²J_PP = 18, 243 Hz), 76.5 (dd, ²J_PP = 18, 29 Hz).

3. Computational Details

All calculations were made with the commercial software Spartan’20 [44]. Starting points for the optimization search were located using the robust PBE/6–31G* method. Geometry optimizations were made using m–GGA functional M06–L functional, the def2–SVPD basis functions, and the CPCM implicit model solvent available in Spartan, using the DICHLOROMETHANE option (ε = 8.93). The energy gradient convergence criterium was tightened from Spartan’s default value 3 × 10⁻⁴ to 5 × 10⁻⁵ erg·bohr⁻¹. Electronic (SCF) energies were refined with a single point calculation at the M06/def2–TZVPPD level, with the SCF convergence criterion set to “HIGH”. All stationary points were checked to have zero (stable intermediates) or one imaginary frequency (transition states). Single-point calculations were accelerated using the “dual basis” option, which specifies that SCF convergence is achieved at the def2–TZVP level and then corrected perturbatively for the effect of additional diffuse and polarization functions. Thermal corrections (TC) were computed at 298.15 (25 °C) and 1 atmosphere. To calculate the solvent correction (SC), we performed an inexpensive additional gas phase single-point energy calculation on optimized geometries at the M06–L/def2–SVPD level (i.e., omitting the solvent calculation), therefore, SC = E(SCF, CPCM) −E(SCF, gas phase), at the M06–L/def2–SVPD level. In addition to reducing the computational cost, this procedure has the advantage of computing the solvent effect at a level of the theory similar to that used for the parametrization of the CPCM model. The refined G° values were calculated for each molecule as G° = E(SCF, M06/def2–TZVPPD) + TC + SC. ZPE-corrected SCF energy data also refer to single-point M06/def2–TZVPPD calculations and include the solvent correction, i.e., E_{(SCF + ZPE)} = E(SCF + SC + ZPE). When the transition states closely resemble that of the highest-energy ground state (e.g., Ni–TS1), the free energy composed by this approximate summation procedure may be slightly below that of this ground state. To avoid this artifact, the free energy of the transition state was computed by adding the difference calculated at the geometry optimization level to that of the highest-lying ground state. Free-energy profiles were generated using the freely available online tool EveRplot [45].

4. Results and Discussion

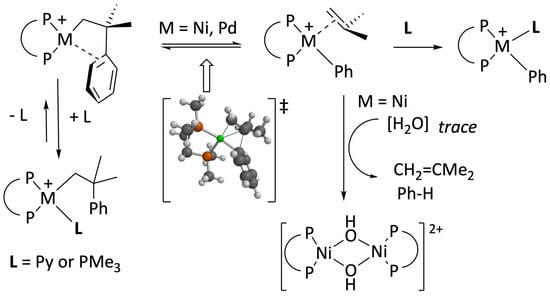
Reactions of nickelacylic complexes 4a,b with acidic derivatives of low-coordination capacity anions. Anticipating the high reactivity and lower kinetic stability of nickel complexes, in this work, we have decided to focus our study on the bulky diphosphine 1,2–bis(diisopropylphosphino)ethane (DiPPE) instead of the less-demanding ligand DMPE, previously used with palladium. In addition, we conducted some experiments with the related ligand 1,3–bis(diisopropylphosphino)propane (DiPPP), which differs only in having one additional methylene group in its backbone. To this end, we used the previously reported [43] nickelacycles 4a and 4b.

Adding one equivalent of triflic acid to cold solutions of either of these metallacycles in diethyl ether leads to yellow suspensions that, on stirring at room temperature for ca. one hour, change to a reddish-orange color. The products were easily isolated in high yields and characterized based on their IR, NMR, and analytical data. These were identified as the binuclear hydroxo-bridged dimeric complexes with the composition [{Ni(μ–OH)(P–P)}₂]²⁺[OTf⁻]₂, 5a and 5b (P–P = DiPPE or DiPPP, see Scheme 3). Their ¹H spectra show a high-field resonance (5a, −1.51 ppm; 5b, −3.27 ppm) for the hydroxyl protons, but no additional signals other than those of the diphosphine ligands were observed in the proton or ¹³C NMR spectra, consistent with the loss of the hydrocarbyl ligand. In anhydrous CD₂Cl₂, the characteristic OH signal of 5a is split in a quintet with J_HP ≈ 2 Hz by coupling with four chemically equivalent ³¹P nuclei. Although the H–P coupling was not resolved in the case of 5b, both complexes exhibit simple ³¹P{¹H} spectra consisting of a single sharp singlet, as expected for their highly symmetrical structures. The characteristic IR absorption bands for the 5a and 5b O–H stretches were observed at 3954 and 3513 cm⁻¹, respectively. In addition, the spectral data for 5a are entirely consistent with those reported by J. García and colleagues, who resolved the crystal structure of this compound [46].

It has been shown that electrophiles, including conventional Brönsted acids, react selectively with nickel or palladium benzometallacyclopentenes of type 4, cleaving the M–aryl bond to yield neophyl derivatives [37,47,48,49]. The course of the reactions of 4a and 4b with triflic acid also fit this trend. However, the initially formed products are unstable, reacting with trace amounts of water to yield the corresponding hydroxides. Accordingly, if the initial yellow precipitate formed from 4a and HOTf is filtered off from the solution, and its ¹H and ³¹P{¹H} NMR spectra are quickly recorded, these show the typical features expected for a non-symmetrical neophylnickel-triflate species, 6. Thus, the ³¹P{¹H} spectrum of 6a displays two doublets (at 57 and 69 ppm; ²J_PP = 9 Hz), and all signals for the nickel-bound neophyl group were identified in the ¹H spectrum. As expected, the signal for the nickel-bound CH₂, observed in the high field region (0.78 ppm), is split into a doublet of doublets by coupling with two chemically inequivalent ³¹P nuclei (14.0 and 4.8 Hz). Similar observations were made for 6b (see the experimental part). The NMR data alone cannot unambiguously tell the exact coordination mode of the neophyl ligand in these complexes. However, no additional signals for coordinated solvent or water were observed in the ¹H spectra of 6a or 6b. As depicted in Scheme 3, complexes 6 could exist as either a neutral species with a sigma ligand (I) or as a cationic species, with an intramolecular π–arene interaction, similar to the Pd complex 1 (II). The chemical shift of the ¹H NMR Ni–CH₂ signal of 6a is unusually upfield-shifted compared to nickel complexes with terminally coordinated neophyl derivatives or the starting metallacycles 4a or 4b (ca. 1.5–2.0 ppm) [43,50]. A similar shielding of the methylene signals is observed in the ¹H NMR spectra of known Pd(II) σ,π–neophyl derivatives, such as 1 [37,39,48]. This suggests that 5a (and possibly 5b) might have an ionic structure of type II. Moreover, a close analog of 6 with a σ,π–neophylnickel cation but supported by the even bulkier diphosphine DtBPE (1,2–(di–t–butylphosphino)ethane) was synthesized and structurally characterized by Hillhouse [51]. Interestingly, this complex was crystallized in the presence of donor solvents THF and Et₂O, yet it has a type II structure. Its Ni–C(ipso) bond, 2.478(4) Å, is quite long, even for a π–bond, which suggests that the arene interaction is weak, probably due to steric repulsions with the DtBPE ligand. Unfortunately, the methylene resonance was not located due to extensive signal overlapping in the ¹H aliphatic region, preventing a comparison with 6a.

Complexes 6a and b are thermally unstable in CD₂Cl₂. The transformation of 6a into the hydroxide 5a is complete within a few hours at room temperature, even if our NMR solvent is routinely dried by refluxing over CaH₂ (see the experimental part). The decomposition was accompanied by the formation of an equimolar amount of isobutene (signals at 1.74 and 4.66 ppm, intensity ratio 3:1) and benzene (7.34 ppm). No t–butylbenzene, the signature of a hypothetic Ni–CH₂ hydrolysis, was detected. The t–Bu of t–butylbenzene would give a conspicuous singlet at ca. 1.31 ppm, next to the CMe₂ resonance of 6a, at 1.40 ppm. These data conclusively demonstrate that the decay of complexes 6 does not involve direct hydrolysis but quantitative β–Ph elimination. Consequently, the hydroxides 5 are formed from the unstable phenyl species arising from it.

To confirm the β–Ph elimination mechanism, we decided to explore the protonation of 4a with the conjugate acids of bases of different coordination strengths that, once deprotonated, could bind to the products. The base–stabilized neophyl intermediates might be stable enough to allow detection or isolation. In the first attempt, we reacted pyridinium triflate with 4a (Scheme 4). The neophyl–pyridine adduct, 7a, also precipitates when the diethyl ether reaction is conducted at −60 °C. The yellow precipitate was collected, and its ¹H and ³¹P{¹H} NMR spectra were recorded in a CD₂Cl₂ solution at room temperature. Although the pyridine ligand enhances its thermal stability, 7a still decays via β–Ph elimination over 24 h, as indicated by the formation of isobutene and the phenyl complex 8a (see Figure 1). Complex 8a was identified based on its ¹H and ³¹P{¹H} NMR spectra, but it could not be isolated pure, as it is prone to hydrolysis and is always contaminated with some hydroxide (5a).

To generate more stable neophyl complexes amenable to complete spectroscopic characterization, we considered replacing pyridine with p–dimethylamino pyridine, a qualitatively similar but stronger electron–donor ligand. Remarkably, p–dimethylamino–pyridinium triflate proved to be an acid too weak to cleave a Ni–C(aryl) bond of metallacycles 4. Therefore, as shown in Scheme 4, we first generated complex 7a, and then the pyridine ligand was exchanged in situ with one equivalent of DMAP. In this way, analytically pure 9a was obtained, with an excellent yield. The latter proved stable in solution and has been fully characterized by the usual ensemble of multinuclear NMR, IR, and elemental analyses. The spectroscopic features of 9a are very similar to those of the thermally sensitive 7a and confirmed the previous assignments based on solution ¹H and ³¹P data only. On the other hand, we have performed preliminary research in the DiPPP system, which confirmed that the same route could be applied to prepare derivatives 7b and 9b. Selected data for the latter two compounds are provided in the Materials and Methods Section.

Cationic organonickel complexes, such as 8, containing diphosphine and pyridine ligands are rare. To our knowledge, only a couple of aryl derivatives of composition [Ni(Ar)(γ–Pic)(DPPE)]⁺(BF₄)⁻ have been briefly mentioned in the literature (γ–Pic = 4 methylpyridine, Ar = mesityl or 3,5–dichlorophenyl) [52,53]. However, the hydrolytic sensitivity of the pyridine–stabilized complex 8a is quite surprising. To test whether this is a general property of organonickel derivatives with this configuration or if it is a specific property of this phenyl complex, we decided to synthesize methyl analogs of 8 by protonation of the known dimethyl complexes [43] [NiMe₂(P—P)] with pyridinium triflate (Scheme 5). The pyridine-containing methyl complexes 10 were isolated and fully characterized. For the sake of completeness, we also report similar data for the corresponding DMAP adducts (11a,b), which were used to help in the spectroscopic assignment of the NMR spectra of the less stable complexes (Scheme 5). All these methylnickel derivatives exhibit normal hydrolytic behavior. Solutions of 10 in dichloromethane can be stored for extended periods without noticeable formation of hydroxide 5a, confirming the high reactivity of the Ni–aryl linkage in this type of cationic complexes. This issue is discussed in more depth in the computational section.

Following a similar approach, we have briefly investigated the reaction of complex 4a with an acidic trimethylphosphonium salt. In this case, we used the crystalline derivative [HPMe₃]⁺[BAr’₄]⁻ (Ar’ = 3,5–C₆H₅(CF₃)₂) for practical reasons. In view of the thermal stability of the DMAP complexes 9, we expected that the interaction 4a with one equivalent of the trimethylphosphonium salt would also yield a stable neophyl derivative, [Ni(CH₂CMe₂Ph)(PMe₃)(DiPPE)]⁺[BAr^F₄]⁻. However, the standard workup of the reaction mixture led to the isolation of the phenyl derivative [Ni(Ph)(PMe₃)(DiPPE)]⁺[BAr’₄]⁻ (12) in high yield, which was readily identified based on its NMR spectra (Scheme 6). This result is surprising because, as mentioned in the introduction, the similar palladium complex [Pd(CH₂CMe₂Ph)(PMe₃)(DMPE)]⁺[BAr’₄]⁻ is indefinitely stable in solution and only decays in the presence of the π–arene complex [Pd(σ,π–CH₂CMe₂Ph)(DMPE)]⁺ (1), which is the agent that spontaneously undergoes β–Ph elimination [39]. The comparatively facile isobutene de-insertion from the nickel neophyl–PMe₃ intermediate poses an intriguing mechanistic problem, as shown in Scheme 6. It could be that the nickel system does not require the intermediacy of the [Ni(σ,π–CH₂CMe₂Ph)(DiPPE)]⁺ cation (III) but proceeds through the pentacoordinate intermediate, IV. The latter might directly experience the β–Ph abstraction to afford complex 12 without PMe₃ dissociation. This mechanism implies the existence of the reverse process involving associative olefin insertion through the same transition state, which might have consequences for some nickel-catalyzed reactions, particularly the Mizoroki–Heck reaction. This possibility will also be addressed in the computational section.

Computational analyses of reaction mechanisms with nickel and palladium. To compare the relative tendencies of nickel and palladium compounds to undergo β–Ph elimination, we chose to compute the energy barriers in the structurally simpler derivatives with DMPE for both palladium and nickel, even when the latter was not investigated. This approach has advantages not only for limiting the conformational cost of modeling the i–Pr substituents but also allows a more realistic comparison of both metals. We chose the M06 family of functionals to perform the analyses because these provide a good description of non-covalent dispersive forces and steric repulsions that likely play a major role in the bonding of π–arene M(II) cations. The less demanding M06–L functional, with a double-z basis, was used for geometry optimization and then complemented with a single-point energy calculation at the M06/triple-zeta quality basis functions level of the theory for energy calculations. The solvent was modeled as dichloromethane through the whole optimization procedure. As a benchmark of the geometry performance of this method, we optimized the geometry of Ni and Pd σ,π–neophyl complexes whose experimental X-ray data were available in the literature [39,51]. These are compared in Figure 2.

As can be seen, there is an excellent concordance between the calculation and the experimental X-ray diffraction data. The mean deviation of the reference values is less than 2% for both the Pd and Ni complexes. Not surprisingly, the most significant differences are found in the M···C(ipso) distance, which reflects the delicate equilibrium between the weak attractive π–arene interaction and the steric interactions with the ligand and packing forces in the solid state. Perhaps for this reason, we found a significant improvement in the π–bond distances by adding diffuse functions (def2–SVPD) to the def2–SVP basis frequently used in geometry optimization. These repulsive forces are maximum for the nickel complex, which bears the bulky DtBPE ligand. The very long Ni···C(ipso) bond predicted by the calculation (2.35 Å) is even longer in the crystal structure (2.48 Å). This suggests that, in this case, crystal packing forces may be distorting the weak π–Ni–arene interaction. For the sake of comparison, Figure S1 lists the π–bond distances computed for the Ni–DMPE (6′), DiPPE, and DtBPE σ,π–neophyl complexes, as well as those of the palladium model 1′ (see the SI for other molecular drawings; the apostrophe is used from now on to distinguish computational models from their experimental counterparts). As can be seen, as the steric bulk of the diphosphine increases, there is an elongation of the π Ni···Ph interaction. This is strongest in 6′, as revealed by shorter π Ni···C(ipso) and Ni····C(ortho) bonds, 2.18 and 2.30 Å, respectively. These distances are comparable to those in typical Ni(II)–π–arene interactions [54,55].

As mentioned before, our NMR data suggest that, at least in 6a, the neophyl ligand likely coordinates in the σ,π–mode, as represented in II, rather than the triflate-alkyl structure of type I (see Scheme 3). To throw light on this issue, we have carefully examined both possible coordination models in the computational model (6′). Previously, we analyzed the different conformations of the neophyl ligand using a molecular mechanics approach with a frozen metal coordination unit. Then, the restrictions were removed, and the geometry of each of the conformers was re-optimized at the usual level of the DFT theory, including the solvent treatment. Seven local minima, four within 1 Kcal/mol on the potential energy surface (Figure S2 and Table S2 in the Supplementary Materials). Two of these (the absolute minimum, M001, and M003) have square-pyramidal geometries, where the basal plane greatly resembles II, and the triflate anion binds at the axial position with a rather Ni···OTf, at ca. 2.3 Å. The rest exhibit more or less square-planar environments of type I, with in-plane Ni–OTf bond lengths of ca. 2.02–2.09 Å and the neophyl fragment adopting various configurations. Although we cannot predict the structure of complexes 6 in the solid state, M001 and M003 could be regarded as contact ion pairs of the π–arene cation 6′ with the triflate anion. The entropy-driven complete dissociation of the triflate anion is granted by the significant exergonic balance, which amounts to −5.7 Kcal/mol relative stable of the pentacoordinate complexes, as represented in Scheme 7. Therefore, nickel complexes of type 6′ would most likely exist in dichloromethane solution as discrete π–arene stabilized ions. The same could be said of their real-world counterpart 6a, in agreement with the above-discussed NMR hints.

For completeness, we repeated this treatment with palladium but did not find pentacoordinate isomers; instead, we found only square-planar complexes. In a further attempt to optimize a pentacoordinate, we optimized a square-pyramidal geometry with a triflate in the apex. However, this led to the square-planar 1′ and a far distant triflate anion (>3 Å). The ionization of [Pd(CH₂CMe₂Ph)(OTf)(DMPE)] in dichloromethane solution into the corresponding 1′ cation and triflate is favorable by −6.7 Kcal/mol, which is close to the equivalent process for the square-planar nickel complexes (i.e., −0.5 + (–5.7) = −6.2 Kcal/mol). Note that, in addition to the internal π–arene interaction, these free energy balances include various other terms, such as the triflate–covalent bond, the electrostatic energy, and steric repulsive forces. Therefore, they cannot be taken as representative of the benzene ring π–binding energy.

A different structural problem that we found in our computational model concerns the structure of the binuclear hydroxide (5a′). As mentioned before, the crystal structure of the DiPPE-containing binuclear hydroxide 5a has been reported in the literature [46]. In the solid state, the dication [Ni(μ–OH)(DiPPE)]₂²⁺ exhibits a flat Ni₂(μ–OH)₂ core, both in the triflate and PF₆^– salts. However, our initial calculations predicted a puckered four-membered Ni₂O₂ ring with a pronounced folding angle of 234.3°. This is expected if the bridging oxygen uses sp³ hybrid orbitals with internal angles of ca. 109°. Yet, flat rings (i.e., with a dihedral angle close to 180°) are a common structural feature in the crystal structures of binuclear, hydroxyl-bridged complexes. A search in the Cambridge Structural Database [56] for binuclear Ni(II) hydroxides with phosphine ligands led to six hits, only one of which (CSD code FAYWAG) deviates significantly from planarity, with a 218° angle [57]. The same paper also reports on a close analog with a planar structure (CSD code FAYTIL). A careful inspection of these two structures shows that the hydroxyl hydrogen atoms in these compounds are in different conformations: on the same side of the Ni₂O₂ ring in FAYWAG and one on each side in FAYTIL. Extending our search to the heavier elements of group 10 led to a total of 33 hits (excluding redundant structures), 28 showing a planar M₂O₂ core, and only 5 having some significant folding. A problem with X-ray data is that, usually, H atoms are not accurately located in the electron density map. Old structures do not even include the hydrogen atom coordinates. When they do, H atoms are allowed to “ride” in a fixed position on their supporting atoms in the refining procedure. For this reason, it cannot be trusted that planar M₂(μ–OH)₂ cores are a real feature. In fact, the hydroxyl H atoms were located on opposite sides of the M₂O₂ ring in three “angular” structures (LEJGUF, REDZIJ, YUNBOY) and none on the same side. Thus, it seems that the angular configuration occasionally observed in binuclear hydroxides of this class probably corresponds with a cisoid disposition of the hydroxyl groups. Accordingly, we set to model both cis and trans configurations for the hypothetical (not yet reported) dication [Ni(μ–OH)(DMPE)]⁺, and the calculations converged in two configurations, cisoid with the above-mentioned angular Ni₂O₂ ring and transoid, where this is essentially flat (Figure 3). The SCF energy favors the angular configuration by 6.7 Kcal/mol at the theory level used in geometry optimization. Still, it gives the opposite result in the high-level single-point calculation (the flat Ni₂O₂ ring being favored by 4.2 Kcal/mol). In terms of free energy, both conformers have nearly the same energy (just 0.4 Kcal/mol difference in favor of the angular), which suggests that the structure is flexible. Either configuration can be selected during the crystal growth process. In our final data, we always refer to the most stable configuration, which happens to be different for Pd, where the flat transoid conformer is favored by about one Kcal/mol.

Once the main features of our model were addressed, we were ready to compare the feasibility of β–Ph elimination in Pd and Ni complexes. Given the prevalence of π–arene cations 1′ and 6′, we can omit the triflate anion from this study and focus on discrete cationic species. The results are summarized in the free-energy profile diagram shown in Figure 4. The profiles for Ni and Pd include the hydrolysis of the putative 14-electron phenyl complexes, even though the second part of the reaction was never experimentally observed for palladium.

The initial part of the mechanism corresponds to the β–Ph elimination. To access the phenyl transfer transition state TS1 from the π–arene species, the metal atom merely shifts from its π–arene coordination to interact with the σ–H₂C–CMe₂(Ph) bond. In the course of this process, the Me₂C–Ph bond weakens, while the vicine Me₂C–CH₂ fragment becomes a coordinated isobutene molecule. As can be seen, this process is mildly endergonic, somewhat more so for nickel than for palladium. However, the energy barrier is substantially lower for Ni (18.2 Kcal/mol) than for palladium (23.9 Kcal/mol). These figures are consistent with the experiment: whereas 1 is relatively stable in solution, stirred suspensions of 6a and 6b decompose spontaneously at room temperature.

As discussed in the introduction, β–Ph elimination can be seen as the reverse of a migratory insertion of the isobutene ligand into the M–Ph bond. Since the phenyl-alkene products have similar stability (Pd, 8.7 vs. Ni, 7.7 vs. Kcal/mol, relative to the π–arenes 1′ and 6′), the energy barrier in the backward direction (namely, the free energy difference between TS1 and the phenyl-alkene complexes) is also smaller for Ni than for Pd. This is in keeping with many experimental and theoretical studies, which regularly report insertion barriers 4–5 Kcal/mol lower for Ni than for Pd. Most likely, the relative height of the energy barriers arises because the intermediates on both sides of TS1 are better stabilized by their π–ligands for Pd than for Ni [58]. This is a consequence of the efficient overlapping of the carbon π orbitals by the 4d orbitals of Pd, compared to the more compact 3d shell of Ni [59].

Because the metal and the incipient phenyl and alkene ligands must be coplanar in the transition state TS1, the π–alkene ligand arises from this step in the “in-plane” conformation. It is known that 16-electron square planar complexes favor an “orthogonal” disposition of the alkene with regard to the ML₃ fragment, as in Zeise’s salt [60,61]. Thus, one would assume that the next logical step in this process is the rotation of the alkene to adopt the latter configuration. However, the situation turns out to be quite different for Ni and Pd. In the latter case, a facile rotation step ensues through the transition state TS2, leading to the slightly more stable π–alkene isomer. However, in the more crowded coordination sphere of the smaller Ni atom, the configuration of the “in-plane” isomer is distorted by steric repulsions, forcing the bulky isobutene to rotate out of the coordination plane. An “orthogonal” ground state still exists, but its structure and energy are very similar to those of TS2. The free energy of this transition state is estimated to be very close to that of the orthogonal product (see Computational Details in the Materials and Methods Section), meaning that the orthogonal π–isobutene ligand is destabilized in the Ni system, favoring its release. In fact, including the entropy for alkene dissociation, the coordinatively unsaturated phenyl species [Ni(Ph)(DMPE)]⁺ lies only 5 Kcal/mol above the latter isomer. For palladium, isobutene dissociation is considerably more endergonic (+8.6 Kcal/mol). Both highly reactive 14-electron [M(Ph)(DMPE)]⁺ fragments can then be trapped by a water molecule as the aqua complexes [62] [M(Ph)(H₂O)(DMPE)]. A water molecule stabilizes the Ni intermediate more efficiently than its Pd counterpart (by 8.8 vs. 5.0 Kcal/mol), preconfiguring a more facile hydrolytic pathway for Ni. Substituting the isobutene ligand with water might also involve an associative process [63,64]. However, we have not explored this pathway, since water is a trace impurity in our system. This aspect of the mechanism is not critical, since the exchange of the π–olefin ligand is, in terms of free energy, moderately downhill along the nickel profile and considerably uphill in the case of Pd. This pre-configures the different hydrolytic behavior of Ni and Pd once the β–Ph step has taken place.

Next, the aqua intermediates undergo intramolecular proton transfer from the coordinated water to the phenyl ligand, leading to monomeric hydroxide complexes stabilized by a π–coordinated benzene ligand. This can be seen as an intramolecular electrophilic attack on the metal-bound carbon atom from the aqua ligand, whose acidity is enhanced by the positively charged metal. This view is supported by the resistance of complexes such as [Ni(Me)(Py)(DiPPE)]⁺ to hydrolysis since the sp³ hybridized methyl carbon atom is less amenable to electrophilic attack. The transition state TS3, corresponding to the X···H···C proton transfer, leads to a monomeric hydroxide stabilized by a π–benzene ligand, which is readily lost in a strongly exergonic step to yield the final binuclear hydroxides. TS3 is similar to that found in the 1,2–C–H addition to M–OR or M–OH bonds, described by Cundari and Gunnoe for Ru complexes [65] and more recently investigated by Schafer and Love for Ni [66]. The free energy barrier to the proton transfer from the aqua precursor is considerably higher for Pd (22.4 Kcal/mol) than for Ni (18.9 Kcal/mol). The different energies of TS3 in the Ni and Pd profiles of the hydrolysis reaction can be rationalized, considering that it involves the formation of a covalent M–OH linkage at the expense of an M–C bond. We have shown in a previous contribution [67] that the Ni–OH bond is stronger than the Pd–OH because of the dipolar contribution from the electrostatic attraction between the compact-sized OH ligand and the smaller metal cation. A similar explanation could also be invoked for the more efficient stabilization of Ni species by water compared to Pd. Overcoming the whole barrier is only feasible for the former (26.9 vs. 34.3 Kcal/mol). Accordingly, no hydrolysis products were formed when the decomposition of complex 1 was thermally induced in the absence of 3. Only isobutene, some Pd black, and ill-defined products were observed [39].

As mentioned previously, 16-electron neophyl nickel complexes, such as the pyridine adduct 7a or its putative PMe₃ analog, also undergo facile β–Ph elimination, even at room temperature, with no need for a catalytic amount of a cationic catalyst such as 6a. This could suggest the possibility of a more direct pathway to β–Ph elimination, operating through a pentacoordinate intermediate of type IV in this case. Given its potential interest in nickel-catalyzed reactions, we have also modeled this route. Interestingly, the conformational analyses of the 16-electron neophyl intermediate [Ni(CH₂CMe₂Ph)(PMe₃)(DMPE)]⁺ revealed the existence of a stable pentacoordinate isomer, IV′, lying only 5 Kcal/mol above its square-planar isomer (Scheme 8). Similar interactions have been experimentally discovered in nickel phosphinoenolato complexes with biphenyl substituents on the P atom [68].

The intermediate IV′ has an approximately trigonal bipyramidal geometry, with the PMe₃ and the π–arene ligands lying in the equatorial plane, while the CH₂ and one of the PMe₂ donor groups are positioned along the axis. Thus, the π–arene interaction, although weak, causes a noticeable distortion of the geometry of the Ni center. An 18-electron transition state, TS4, connects IV′ with the corresponding phenyl-isobutene complex, 13′. Interestingly, the Ni–PMe₃ interaction fades on going from IV′ to TS4 and then to 13′, as reflected by the long Ni–P distances, 2.60 Å and more than 3 Å, respectively. The latter can be regarded as fully dissociated. Then, a facile exchange of the olefin ligand with the nearby PMe₃ would lead to the phenyl-phosphine product 12′. We located the corresponding transition state, TS5, which is not shown in the scheme for simplicity (the free-energy profile is provided in the Supplementary Material, Figure S3). The whole process is exergonic by −9.3 Kcal/mol. Therefore, the direct non-dissociative mechanism is a possibility for β–Ph elimination. However, a closer examination of the mechanism shown in Scheme 8 indicates this is highly unlikely.

The main drawback of the above mechanism is the unrealistic high energy barrier (ΔG^‡) that TS4 poses to the β–Ph elimination from IV′. Assuming that the 16-electron neophyl–PMe₃ complex is in equilibrium with IV′, the overall barrier would be 27.5 + 5.0 = 32.5 Kcal/mol, which is not accessible at room temperature. Notice that the reversal, i.e., associative carbometallation, is even less likely (this is best appreciated in Figure S3). This is mainly due to the prohibitive energy cost of temporarily displacing PMe₃ with such a poor ligand as isobutene.

As an alternative, we investigated the feasibility of a dissociative mechanism involving the initial release of a PMe₃ ligand. For this purpose, it is helpful to consider the dissociative equilibria shown in Scheme 9.

As can be seen, this mechanism involves the displacement of the monodentate PMe₃ ligand by the phenyl fragment of the alkyl. The reaction heat (represented here by the conceptually more accurate zero-point-corrected energy balance, ΔE_SCF+ZPE) is strongly endothermic. However, the entropy contribution due to the release of PMe₃ ligand offsets the unfavorable energy change, and the dissociation is mildly endergonic. For Ni, PMe₃ dissociation is further favored by the weaker ligand bonding in the 3d series and by the strain release due to the small size of the Ni atom. The latter is probably more acute with the bulkier diphosphine DiPP used in the experiment.

Assuming that the phosphine dissociation that leads to the π–arene intermediate is a fast equilibrium, its free energy variation (ΔG°) adds to the energy barrier for the rate-limiting β–Ph elimination (ΔG^‡) to compose the actual energy barrier for the whole elimination process, as shown in Scheme 9. In agreement with our experimental observations, the overall barrier (ΔG° + ΔG^‡) is too high for the Pd complex (30.2 Kcal/mol). For Ni, it is only 20.5 Kcal/mol, low enough to assume a spontaneous reaction at a mild temperature. Moreover, the availability of the five-coordinated species IV′ indicates that PMe₃ could be displaced through an intramolecular “associative” mechanism rather than undergoing spontaneous dissociation. The energy barrier for the Ni preequilibrium would be only slightly above that of IV′ (≈5 Kcal/mol). On the contrary, we could not locate a pentacoordinate intermediate or a similar intramolecular transition state to access 1′; we are forced to believe that direct dissociation of PMe₃ would be required to enable β–Ph elimination from the Pd complex. Even if this difficulty is neglected, the composed barrier would be too high at room temperature, which explains the experimentally observed need to bait the PMe₃ complex [PdCH₂CMe₂Ph(PMe₃)(DMPE)] (3) with a catalytic amount of 1 to enable a productive β–Ph reaction to proceed [39].

5. Conclusions

We have shown that, similar to their Pd counterparts, Ni–neophyl complexes are also prone to undergo irreversible transformations triggered by β–Ph elimination, the microscopic reverse of olefin migratory insertion into an M–Ph bond. Neophylnickel triflate complexes 5a and 5b containing a chelating diphosphine (DiPPE or DiPPP) were generated at low temperatures by protonating the metalacyclic precursors 4a and 4b with triflic acid. These complexes probably feature a π–arene interaction that promotes β–Ph elimination. Traces of water trap the resulting phenyl-nickel species to yield the binuclear hydroxo-bridged dimers 4a and 4b, which greatly facilitated the elucidation of the whole process.

The 16-electron neophylnickel cations of the type [Ni(CH₂CMe₂Ph)(L)(P–P)]⁺ (L = monodentate base) also undergo β–Ph elimination. The coordinating strength of the ancillary ligand L can modulate the stability of such complexes. A qualitative stability order, L = none < Py, PMe₃ < DMAP, emerges from these experiments. For L = Py or PMe₃, the decomposition still occurs readily at room temperature, in contrast with the thermally stable Pd cation [Pd(CH₂CMe₂Ph)(PMe₃)(DMPE)]⁺, previously reported by our group. This suggests that β–Ph elimination is kinetically easier for nickel neophyl derivatives than their Pd analogs.

DFT calculations support the above conclusions. A comparison of the β–Ph elimination step in the isostructural Pd and Ni DMPE models 1′ and 6′ draws a significantly lower barrier for the latter, even though the elimination step is somewhat more thermodynamically favorable for the former. While the instability of the square-planar 16-electron adducts of pyridine and PMe₃ suggested that phenyl abstraction, similar to β–H elimination, might proceed directly via a pentacoordinate transition state, this study has shown that the energy of this latter is prohibitively high. Instead, the dissociation of the ligand L (presumably assisted by the phenyl fragment) does explain our experimental observations. Since β–Ph elimination is the microscopic reverse of olefin carbometallation, the latter conclusion is in line with the dearth of literature examples of direct carbometallation via five-coordinated transition states.

An additional lesson to be learned from this study is that nickel complexes are often more sensitive to hydrolytic decay compared to their palladium counterparts. The facile trapping of the phenyl–Ni species by water results from the stronger Ni–OH bond and the relatively facile intramolecular H transfer from a coordinated aqua complex to the Ni–bound Ph, whose energy barrier is significantly higher for palladium. The facile hydrolysis of nickel–aryl complexes suggests that strict anhydrous conditions may prove more critical for catalytic applications of nickel compounds, particularly those involving nickel catalysts in cationic Mizoroki–Heck reactions.