A Raman Spectroscopic and Computational Study of New Aromatic Pyrimidine-Based Halogen Bond Acceptors
Abstract
:1. Introduction
2. Results
2.1. Experimental Results
2.2. Computational Results
3. Discussion
3.1. Effect of Furan and Thiophene Moieties on Pyrimidine’s Normal Modes
3.1.1. Ring Puckering Mode ν16a
3.1.2. Ring Bending Modes ν6b and ν6a
3.1.3. Fermi Resonance and Ring Breathing Modes ν1 and ν12
3.1.4. NCN Bending Mode ν9a and In-Plane CH Bending Mode ν3
3.1.5. Symmetric and Asymmetric CN Stretching Modes ν8a and ν8b
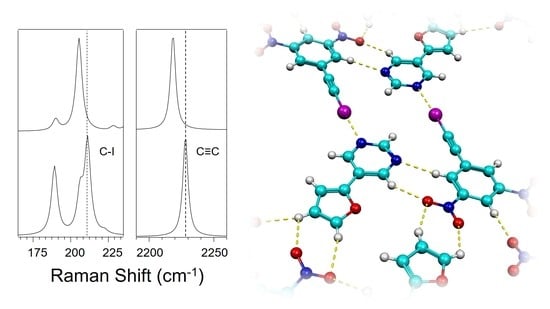
3.2. Effect of Halogen Bond Interactions on Raman Spectral Features
4. Materials and Methods
4.1. Synthesis and Co-Crystallization
4.2. Spectroscopic Details
4.3. Computational Details
4.4. X-ray Crystallography
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Jheng, J.-F.; Lai, Y.-Y.; Wu, J.-S.; Chao, Y.-H.; Wang, C.-L.; Hsu, C.-S. Influences of the Non-Covalent Interaction Strength on Reaching High Solid-State Order and Device Performance of a Low Bandgap Polymer with Axisymmetrical Structural Units. Adv. Mater. 2013, 25, 2445–2451. [Google Scholar] [CrossRef] [PubMed]
- Wang, D.; Tong, G.; Dong, R.; Zhou, Y.; Shen, J.; Zhu, X. Self-assembly of supramolecularly engineered polymers and their biomedical applications. Chem. Commun. 2014, 50, 11994–12017. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, T.L.; Choi, H.; Ko, S.J.; Uddin, M.A.; Walker, B.; Yum, S.; Jeong, J.E.; Yun, M.H.; Shin, T.J.; Hwang, S.; et al. Semi-crystalline photovoltaic polymers with efficiency exceeding 9% in a ~300 nm thick conventional single-cell device. Energy Environ. Sci. 2014, 7, 3040–3051. [Google Scholar] [CrossRef]
- Feringán, B.; Romero, P.; Serrano, J.L.; Folcia, C.L.; Etxebarria, J.; Ortega, J.; Termine, R.; Golemme, A.; Giménez, R.; Sierra, T. H-Bonded Donor-Acceptor Units Segregated in Coaxial Columnar Assemblies: Toward High Mobility Ambipolar Organic Semiconductors. J. Am. Chem. Soc. 2016, 138, 12511–12518. [Google Scholar] [CrossRef] [PubMed]
- Fang, R.; Chen, R.; Gao, J.; Zhang, H.; Wu, H.; Li, H. Chalcogen bridged pyrene derivatives: Synthesis, crystal–packing structures and field effect transistors properties. Org. Electron. 2017, 45, 108–114. [Google Scholar] [CrossRef]
- Liu, H.; Huang, L.; Cheng, X.; Hu, A.; Xu, H.; Chen, L.; Chen, Y. N-type Self-Doping of Fluorinate Conjugated Polyelectrolytes for Polymer Solar Cells: Modulation of Dipole, Morphology, and Conductivity. Acs Appl. Mater. Interfaces 2017, 9, 1145–1153. [Google Scholar] [CrossRef] [PubMed]
- Metrangolo, P.; Meyer, F.; Pilati, T.; Resnati, G.; Terraneo, G. Halogen Bonding in Supramolecular Chemistry. Angew. Chem. Int. Ed. 2008, 47, 6114–6127. [Google Scholar] [CrossRef]
- Abate, A.; Biella, S.; Cavallo, G.; Meyer, F.; Neukirch, H.; Metrangolo, P.; Pilati, T.; Resnati, G.; Terraneo, G. Halide anions driven self-assembly of haloperfluoroarenes: Formation of one-dimensional non-covalent copolymers. J. Fluor. Chem. 2009, 130, 1171–1177. [Google Scholar] [CrossRef]
- Cariati, E.; Cavallo, G.; Forni, A.; Leem, G.; Metrangolo, P.; Meyer, F.; Pilati, T.; Resnati, G.; Righetto, S.; Terraneo, G.; et al. Self-Complementary Nonlinear Optical-Phores Targeted to Halogen Bond-Driven Self-Assembly of Electro-Optic Materials. Cryst. Growth Des. 2011, 11, 5642–5648. [Google Scholar] [CrossRef]
- Marti-Rujas, J.; Colombo, L.; Lu, J.; Dey, A.; Terraneo, G.; Metrangolo, P.; Pilati, T.; Resnati, G. Hydrogen and halogen bonding drive the orthogonal self-assembly of an organic framework possessing 2D channels. Chem. Commun. 2012, 48, 8207–8209. [Google Scholar] [CrossRef] [Green Version]
- Priimagi, A.; Cavallo, G.; Metrangolo, P.; Resnati, G. The Halogen Bond in the Design of Functional Supramolecular Materials: Recent Advances. Acc. Chem. Res. 2013, 46, 2686–2695. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vasylyeva, V.; Nayak, S.K.; Terraneo, G.; Cavallo, G.; Metrangolo, P.; Resnati, G. Orthogonal halogen and hydrogen bonds involving a peptide bond model. CrystEngComm 2014, 16, 8102–8105. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mukherjee, A.; Tothadi, S.; Desiraju, G.R. Halogen Bonds in Crystal Engineering: Like Hydrogen Bonds yet Different. Acc. Chem. Res. 2014, 47, 2514–2524. [Google Scholar] [CrossRef] [PubMed]
- Wilson, J.; Dal Williams, J.S.; Petkovsek, C.; Reves, P.; Jurss, J.W.; Hammer, N.I.; Tschumper, G.S.; Watkins, D.L. Synergistic effects of halogen bond and π–π interactions in thiophene-based building blocks. RSC Adv. 2015, 5, 82544–82548. [Google Scholar] [CrossRef]
- Vanderkooy, A.; Taylor, M.S. Solution-Phase Self-Assembly of Complementary Halogen Bonding Polymers. J. Am. Chem. Soc. 2015, 137, 5080–5086. [Google Scholar] [CrossRef]
- Bushuyev, O.S.; Tan, D.; Barrett, C.J.; Friscic, T. Fluorinated azobenzenes with highly strained geometries for halogen bond-driven self-assembly in the solid state. CrystEngComm 2015, 17, 73–80. [Google Scholar] [CrossRef]
- Nguyen, S.T.; Rheingold, A.L.; Tschumper, G.S.; Watkins, D.L. Elucidating the Effects of Fluoro and Nitro Substituents on Halogen Bond Driven Assemblies of Pyridyl-Capped π-Conjugated Molecules. Cryst. Growth Des. 2016, 16, 6648–6653. [Google Scholar] [CrossRef]
- Nguyen, S.T.; Ellington, T.L.; Allen, K.E.; Gorden, J.D.; Rheingold, A.L.; Tschumper, G.S.; Hammer, N.I.; Watkins, D.L. Systematic Experimental and Computational Studies of Substitution and Hybridization Effects in Solid-State Halogen Bonded Assemblies. Cryst. Growth Des. 2018, 18, 3244–3254. [Google Scholar] [CrossRef]
- Johnson, S.N.; Ellington, T.L.; Ngo, D.T.; Nevarez, J.L.; Sparks, N.; Rheingold, A.L.; Watkins, D.L.; Tschumper, G.S. Probing non-covalent interactions driving molecular assembly in organo-electronic building blocks. CrystEngComm 2019, 21, 3151–3157. [Google Scholar] [CrossRef]
- Desiraju, G.R.; Shing Ho, P.; Kloo, L.; Legon, A.C.; Marquardt, R.; Metrangolo, P.; Politzer, P.; Resnati, G.; Rissanen, K. Definition of the halogen bond (IUPAC recommendations 2013). Pure Appl. Chem. 2013, 85, 1711–1713. [Google Scholar] [CrossRef]
- Ellington, T.L.; Reves, P.L.; Simms, B.L.; Wilson, J.L.; Watkins, D.L.; Tschumper, G.S.; Hammer, N.I. Quantifying the Effects of Halogen Bonding by Haloaromatic Donors on the Acceptor Pyrimidine. ChemPhysChem 2017, 18, 1267–1273. [Google Scholar] [CrossRef]
- Huang, Y.; Wang, Z.; Chen, Z.; Zhang, Q. Organic Cocrystals: Beyond Electrical Conductivities and Field-Effect Transistors (FETs). Angew. Chem. Int. Ed. 2019, 58, 9696–9711. [Google Scholar] [CrossRef] [PubMed]
- Metrangolo, P.; Resnati, G.; Pilati, T.; Liantonio, R.; Meyer, F. Engineering functional materials by halogen bonding. J. Polym. Sci. Part. A Polym. Chem. 2007, 45, 1–15. [Google Scholar] [CrossRef]
- Cavallo, G.; Metrangolo, P.; Milani, R.; Pilati, T.; Priimagi, A.; Resnati, G.; Terraneo, G. The Halogen Bond. Chem. Rev. 2016, 116, 2478–2601. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Weldeab, A.O.; Steen, A.; Starkenburg, D.J.; Williams, J.S.D.; Abboud, K.A.; Xue, J.; Hammer, N.I.; Castellano, R.K.; Watkins, D.L. Tuning the structural and spectroscopic properties of donor-acceptor-donor oligomers via mutual X-bonding, H-bonding, and π–π interactions. J. Mater. Chem. C 2018, 6, 11992–12000. [Google Scholar] [CrossRef]
- Baumann, A.; Cheema, H.; Sabuj, M.A.; McNamara, L.E.; Zhang, Y.; Peddapuram, A.; Nguyen, S.T.; Watkins, D.L.; Hammer, N.I.; Rai, N.; et al. Iodine binding with thiophene and furan based dyes for DSCs. Phys. Chem. Chem. Phys. 2018, 20, 17859–17870. [Google Scholar] [CrossRef] [PubMed]
- Simon, S.J.C.; Parlane, F.G.L.; Swords, W.B.; Kellett, C.W.; Du, C.; Lam, B.; Dean, R.K.; Hu, K.; Meyer, G.J.; Berlinguette, C.P. Halogen Bonding Promotes Higher Dye-Sensitized Solar Cell Photovoltages. J. Am. Chem. Soc. 2016, 138, 10406–10409. [Google Scholar] [CrossRef]
- Zhu, W.; Zheng, R.; Zhen, Y.; Yu, Z.; Dong, H.; Fu, H.; Shi, Q.; Hu, W. Rational Design of Charge-Transfer Interactions in Halogen-Bonded Co-crystals toward Versatile Solid-State Optoelectronics. J. Am. Chem. Soc. 2015, 137, 11038–11046. [Google Scholar] [CrossRef] [PubMed]
- Zhuo, M.-P.; Tao, Y.-C.; Wang, X.-D.; Wu, Y.; Chen, S.; Liao, L.-S.; Jiang, L. 2D Organic Photonics: An Asymmetric Optical Waveguide in Self-Assembled Halogen-Bonded Cocrystals. Angew. Chem. 2018, 130, 11470–11474. [Google Scholar] [CrossRef]
- Gidron, O.; Diskin-Posner, Y.; Bendikov, M. α-Oligofurans. J. Am. Chem. Soc. 2010, 132, 2148–2150. [Google Scholar] [CrossRef]
- Tibaoui, T.; Ayachi, S.; Chemek, M.; Alimi, K. New bridged oligofuran for optoelectronic applications. Spectrochim. Acta. Part. AMol. Biomol. Spectrosc. 2015, 142, 25–33. [Google Scholar] [CrossRef]
- Xiong, Y.; Wang, M.; Qiao, X.; Li, J.; Li, H. Syntheses and properties of π-conjugated oligomers containing furan-fused and thiophene-fused aromatic units. Tetrahedron 2015, 71, 852–856. [Google Scholar] [CrossRef]
- Walker, B.; Tamayo, A.B.; Dang, X.-D.; Zalar, P.; Seo, J.H.; Garcia, A.; Tantiwiwat, M.; Nguyen, T.-Q. Nanoscale Phase Separation and High Photovoltaic Efficiency in Solution-Processed, Small-Molecule Bulk Heterojunction Solar Cells. Adv. Funct. Mater. 2009, 19, 3063–3069. [Google Scholar] [CrossRef]
- Woo, C.H.; Beaujuge, P.M.; Holcombe, T.W.; Lee, O.P.; Fréchet, J.M.J. Incorporation of Furan into Low Band-Gap Polymers for Efficient Solar Cells. J. Am. Chem. Soc. 2010, 132, 15547–15549. [Google Scholar] [CrossRef] [PubMed]
- Gidron, O.; Dadvand, A.; Sheynin, Y.; Bendikov, M.; Perepichka, D.F. Towards “green” electronic materials. α-Oligofurans as semiconductors. Chem. Commun. 2011, 47, 1976–1978. [Google Scholar] [CrossRef] [PubMed]
- Ferron, C.C.; Delgado, M.C.R.; Gidron, O.; Sharma, S.; Sheberla, D.; Sheynin, Y.; Bendikov, M.; Navarrete, J.T.L.; Hernandez, V. α-Oligofurans show a sizeable extent of π-conjugation as probed by Raman spectroscopy. Chem. Commun. 2012, 48, 6732–6734. [Google Scholar] [CrossRef] [PubMed]
- Gidron, O.; Varsano, N.; Shimon, L.J.W.; Leitus, G.; Bendikov, M. Study of a bifuran vs. bithiophene unit for the rational design of π-conjugated systems. What have we learned? Chem. Commun. 2013, 49, 6256–6258. [Google Scholar] [CrossRef]
- Gidron, O.; Bendikov, M. α-Oligofurans: An Emerging Class of Conjugated Oligomers for Organic Electronics. Angew. Chem. Int. Ed. 2014, 53, 2546–2555. [Google Scholar] [CrossRef]
- Sheberla, D.; Patra, S.; Wijsboom, Y.H.; Sharma, S.; Sheynin, Y.; Haj-Yahia, A.-E.; Barak, A.H.; Gidron, O.; Bendikov, M. Conducting polyfurans by electropolymerization of oligofurans. Chem. Sci. 2015, 6, 360–371. [Google Scholar] [CrossRef]
- Huang, J.-D.; Wen, S.-H.; Deng, W.-Q.; Han, K.-L. Simulation of Hole Mobility in α-Oligofuran Crystals. J. Phys. Chem. B 2011, 115, 2140–2147. [Google Scholar] [CrossRef]
- Steen, A.E.; Ellington, T.L.; Nguyen, S.T.; Balasubramaniam, S.; Chandrasiri, I.; Delcamp, J.H.; Tschumper, G.S.; Hammer, N.I.; Watkins, D.L. Characterization of Furan- and Thiophene-Containing Bispyridyl Oligomers via Spectroscopic, Electrochemical, and TD-DFT Methods. J. Phys. Chem. C 2019, 123, 15176–15185. [Google Scholar] [CrossRef]
- Howard, A.A.; Tschumper, G.S.; Hammer, N.I. Effects of hydrogen bonding on vibrational normal modes of pyrimidine. J. Phys. Chem. A 2010, 114, 6803–6810. [Google Scholar] [CrossRef] [PubMed]
- Howard, J.C.; Hammer, N.I.; Tschumper, G.S. Structures, energetics and vibrational frequency shifts of hydrated pyrimidine. ChemPhysChem 2011, 12, 3262–3273. [Google Scholar] [CrossRef] [PubMed]
- Wright, A.M.; Joe, L.V.; Howard, A.A.; Tschumper, G.S.; Hammer, N.I. Spectroscopic and computational insight into weak noncovalent interactions in crystalline pyrimidine. Chem. Phys. Lett. 2011, 501, 319–323. [Google Scholar] [CrossRef]
- Wright, A.M.; Howard, A.A.; Howard, J.C.; Tschumper, G.S.; Hammer, N.I. Charge transfer and blue shifting of vibrational frequencies in a hydrogen bond acceptor. J. Phys. Chem. A 2013, 117, 5435–5446. [Google Scholar] [CrossRef]
- Kelly, J.T.; Xu, S.; Graham, J.; Nilles, J.M.; Radisic, D.; Buonaugurio, A.M.; Bowen, K.H.; Hammer, N.I.; Tschumper, G.S. Photoelectron Spectroscopic and Computational Study of Hydrated Pyrimidine Anions. J. Phys. Chem. A 2014, 118, 11901–11907. [Google Scholar] [CrossRef]
- DeBlase, A.F.; Wolke, C.; Weddle, G.H.; Archer, K.; Jordan, K.; Kelly, J.T.; Tschumper, G.S.; Hammer, N.I.; Johnson, M.A. Water network-mediated, electron-induced proton transfer in anionic [C5H5N·(H2O)n]− clusters. J. Chem. Phys. 2015, 143, 144305. [Google Scholar] [CrossRef]
- Kelly, J.T.; McClellan, A.K.; Joe, L.V.; Wright, A.M.; Lloyd, L.T.; Tschumper, G.S.; Hammer, N.I. Competition between Hydrophilic and Argyrophilic Interactions in Surface Enhanced Raman Spectroscopy. ChemPhysChem 2016, 17, 2782–2786. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, X.; Lyapustina, S.; Nilles, M.M.; Xu, S.; Graham, J.D.; Bowen, K.H.; Kelly, J.T.; Tschumper, G.S.; Hammer, N.I. The onset of electron-induced proton-transfer in hydrated azabenzene cluster anions. Phys. Chem. Chem. Phys. 2016, 18, 704–712. [Google Scholar] [CrossRef]
- Rahm, M.; Hoffmann, R.; Ashcroft, N.W. Atomic and Ionic Radii of Elements 1–96. Chem. A Eur. J. 2016, 22, 14625–14632. [Google Scholar] [CrossRef]
- Hendsbee, A.D.; Sun, J.-P.; McCormick, T.M.; Hill, I.G.; Welch, G.C. Unusual loss of electron mobility upon furan for thiophene substitution in a molecular semiconductor. Org. Electron. 2015, 18, 118–125. [Google Scholar] [CrossRef]
- NIST. NIST Standard Reference Database 101: Computational Chemistry Comparison and Benchmark DataBase; Release 20 ed.; National Institute of Standards and Technology (NIST): Gaithersburg, MD, USA, 2019.
- Lord, R.C.; Marston, A.L.; Miller, F.A. Infra-red and Raman spectra ot the diazines. Spectrochim. Acta 1957, 9, 113–125. [Google Scholar] [CrossRef]
- Verbitskiy, E.V.; Rusinov, G.L.; Charushin, V.N.; Chupakhin, O.N.; Cheprakova, E.M.; Slepukhin, P.A.; Pervova, M.G.; Ezhikova, M.A.; Kodess, M.I. Consecutive SNH and Suzuki-Miyaura Cross-Coupling Reactions—An Efficient Synthetic Strategy to Pyrimidines Bearing Pyrrole and Indole Fragments. Eur. J. Org. Chem. 2012, 2012, 6612–6621. [Google Scholar]
- Li, J.-H.; Zhu, Q.-M.; Xie, Y.-X. Pd(OAc)2/DABCO-catalyzed Suzuki–Miyaura cross-coupling reaction in DMF. Tetrahedron 2006, 62, 10888–10895. [Google Scholar] [CrossRef]
- Boys, S.F.; Bernardi, F. The calculation of small molecular interactions by the differences of separate total energies. Some procedures with reduced errors. Mol. Phys. 1970, 19, 553–566. [Google Scholar] [CrossRef]
- Simon, S.; Duran, M.; Dannenberg, J.J. How does basis set superposition error change the potential surfaces for hydrogen-bonded dimers? J. Chem. Phys. 1996, 105, 11024–11031. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16 Rev. C.01. 2016. Available online: https://gaussian.com/relnotes/ (accessed on 30 September 2019).
- Zhao, Y.; Truhlar, D.G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theor. Chem. Acc. 2008, 120, 215–241. [Google Scholar]
- Dunning, T.H. Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen. J. Chem. Phys. 1989, 90, 1007–1023. [Google Scholar] [CrossRef]
- Kendall, R.A.; Dunning, T.H.; Harrison, R.J. Electron affinities of the first-row atoms revisited. Systematic basis sets and wave functions. J. Chem. Phys. 1992, 96, 6796–6806. [Google Scholar] [CrossRef]
- Woon, D.E.; Dunning, T.H. Gaussian basis sets for use in correlated molecular calculations. III. The atoms aluminum through argon. J. Chem. Phys. 1993, 98, 1358–1371. [Google Scholar] [CrossRef] [Green Version]
- Peterson, K.A.; Shepler, B.C.; Figgen, D.; Stoll, H. On the Spectroscopic and Thermochemical Properties of ClO, BrO, IO, and Their Anions. J. Phys. Chem. A 2006, 110, 13877–13883. [Google Scholar] [CrossRef] [PubMed]
- Peterson, K.A.; Figgen, D.; Goll, E.; Stoll, H.; Dolg, M. Systematically convergent basis sets with relativistic pseudopotentials. II. Small-core pseudopotentials and correlation consistent basis sets for the post-d group 16–18 elements. J. Chem. Phys. 2003, 119, 11113–11123. [Google Scholar] [CrossRef]
- Kozuch, S.; Martin, J.M.L. Halogen Bonds: Benchmarks and Theoretical Analysis. J. Chem. Theory Comput. 2013, 9, 1918–1931. [Google Scholar] [CrossRef] [PubMed]
- Dolomanov, O.V.; Bourhis, L.J.; Gildea, R.J.; Howard, J.A.K.; Puschmann, H. OLEX2: A complete structure solution, refinement and analysis program. J. Appl. Crystallogr. 2009, 42, 339–341. [Google Scholar] [CrossRef]
- Sheldrick, G. A short history of SHELX. Acta Crystallogr. Sect. A 2008, 64, 112–122. [Google Scholar] [CrossRef]












| Co-Crystal | (NO2)2BAI-PrmF | (NO2)2BAI-PrmT a |
|---|---|---|
| M (g mol−1) | 464.2 | 960.5 |
| Temperature (K) Space Group | 100.0 P | 100.0 P 21/n |
| a (Å) | 6.9398(10) | 9.2195(6) |
| b (Å) | 16.126(2) | 5.7344(4) |
| c (Å) | 18.517(3) | 32.1204(16) |
| α (°) | 79.34 | 90.00 |
| β (°) | 80.01 | 93.21 |
| γ (°) | 89.24 | 90.00 |
| V (Å3) | 2005.2 | 1695.5 |
| Z | 4 | 2 |
| R Factor (%) | 4.84 | 4.38 |
| Mode in Pyrimidine | Building Block | Computed Frequency | Experimental Frequency | Dominant Motion or Character |
|---|---|---|---|---|
| ν16a | Prm | 392 | 400 | Out-of-plane puckering |
| PrmF | 394 | 400 | ||
| PrmT | 400 | 425 | ||
| ν6b | Prm | 606 | 628 | In-plane CCC/NCN bending mode |
| PrmF | 614 | 630 | ||
| PrmT | 615 | 629 | ||
| ν6a | Prm | 667 | 680 | In-plane CCC/CNC bending mode |
| PrmF | 722 | 736 | ||
| PrmT | 723 | 739 | ||
| ν1 | Prm | 980 | 992 | Ring breathing |
| PrmF | 895 | 907 | ||
| PrmT | 946 | 957 | ||
| ν12 | Prm | - | - | Ring bending |
| PrmF | 1043 | 1060 | ||
| PrmT | 1030 | 1051 | ||
| ν9a | Prm | 1126 | 1142 | NCN bend |
| PrmF | 1121 | 1125 | ||
| PrmT | 1120 | 1125 | ||
| ν8b | Prm | 1582 | 1577 | CN stretch |
| PrmF | 1557/1579 | 1555/1569 | ||
| PrmT | 1556 | 1553 | ||
| ν8a | Prm | 1584 | 1568 | CC and CN stretch |
| PrmF | 1606 | 1598 | ||
| PrmT | 1589 | 1583 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hardin, A.E.S.; Ellington, T.L.; Nguyen, S.T.; Rheingold, A.L.; Tschumper, G.S.; Watkins, D.L.; Hammer, N.I. A Raman Spectroscopic and Computational Study of New Aromatic Pyrimidine-Based Halogen Bond Acceptors. Inorganics 2019, 7, 119. https://doi.org/10.3390/inorganics7100119
Hardin AES, Ellington TL, Nguyen ST, Rheingold AL, Tschumper GS, Watkins DL, Hammer NI. A Raman Spectroscopic and Computational Study of New Aromatic Pyrimidine-Based Halogen Bond Acceptors. Inorganics. 2019; 7(10):119. https://doi.org/10.3390/inorganics7100119
Chicago/Turabian StyleHardin, April E. S., Thomas L. Ellington, Suong T. Nguyen, Arnold L. Rheingold, Gregory S. Tschumper, Davita L. Watkins, and Nathan I. Hammer. 2019. "A Raman Spectroscopic and Computational Study of New Aromatic Pyrimidine-Based Halogen Bond Acceptors" Inorganics 7, no. 10: 119. https://doi.org/10.3390/inorganics7100119
APA StyleHardin, A. E. S., Ellington, T. L., Nguyen, S. T., Rheingold, A. L., Tschumper, G. S., Watkins, D. L., & Hammer, N. I. (2019). A Raman Spectroscopic and Computational Study of New Aromatic Pyrimidine-Based Halogen Bond Acceptors. Inorganics, 7(10), 119. https://doi.org/10.3390/inorganics7100119