Next Article in Journal
99mTc Labelling Strategies for the Development of Potential Nitroimidazolic Hypoxia Imaging Agents
Next Article in Special Issue
Influence of Substituents in Terephthalate Linker on the Structure of MOFs Obtained from Presynthesized Heterometallic Complex
Previous Article in Journal
An Optical Power Limiting and Ultrafast Photophysics Investigation of a Series of Multi-Branched Heavy Atom Substituted Fluorene Molecules
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Inorganics
Volume 7
Issue 10
10.3390/inorganics7100127
inorganics-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Heterobimetallic Chromium Manganese Carbonyl Nitrosyls: Comparison with Isoelectronic Homometallic Binuclear Chromium Carbonyl Nitrosyls and Manganese Carbonyls

by
Guoliang Li
1,2,*,
Limei Wen
1 and
R. Bruce King
2,*
1
Key Laboratory of Theoretical Chemistry of the Environment, Ministry of Education; Center for Computational Quantum Chemistry, School of Chemistry and Environment, South China Normal University, Guangzhou 510006, China
2
Department of Chemistry and Center for Computational Quantum Chemistry, University of Georgia, Athens, GA 30602, USA
*
Authors to whom correspondence should be addressed.
Inorganics 2019, 7(10), 127; https://doi.org/10.3390/inorganics7100127
Submission received: 28 August 2019 / Revised: 10 October 2019 / Accepted: 14 October 2019 / Published: 21 October 2019
(This article belongs to the Special Issue Heterometallic Complexes)
Browse Figures
Versions Notes

Abstract

:
The heterometallic chromium-manganese carbonyl nitrosyls CrMn(NO)(CO)n (n = 9, 8) have been investigated by density functional theory. The lowest energy CrMn(NO)(CO)9 structures have unbridged staggered conformations with a ~2.99 Å Cr–Mn single bond similar to the experimental and lowest energy structures of the isoelectronic Mn2(CO)10 and Cr2(NO)2(CO)8. A significantly higher energy CrMn(NO)(CO)9 isomer has a nearly symmetrical bridging nitrosyl group and a very weakly semibridging carbonyl group. The two lowest energy structures of the unsaturated CrMn(NO)(CO)8 have a five-electron donor bridging η2-µ-NO nitrosyl group or a four-electron donor bridging η2-µ-CO group, as well as a Cr–Mn single bond of length ~2.94 Å. The next higher energy CrMn(NO)(CO)8 structure has exclusively terminal CO and NO ligands and a shorter Cr–Mn single bond of ~2.85 Å, suggesting an 18-electron configuration for the manganese atom and a 16-electron configuration for the chromium atom indicated by a vacant coordination site nearly perpendicular to the Cr–Mn bond.

Graphical Abstract

1. Introduction

The isoelectronic bimetallic molecules Mn2(CO)10 and Cr2(NO)2(CO)8 have been known for some time [1]. Thus, Mn2(CO)10 can be synthesized by the reductive carbonylation of manganese(II) derivatives using sodium benzophenone ketyl [2] or triisobutylaluminum [3] as the reducing agent at elevated carbon monoxide pressure. In addition, an atmospheric pressure synthesis of Mn2(CO)10 is possible using the reductive carbonylation of the formerly (but not now) readily available (η5-MeC5H4)Mn(CO)3 with sodium metal in diglyme solution [4]. The isoelectronic Cr2(NO)2(CO)8 can be synthesized by oxidation of the Cr(NO)(CO)4− anion with [(C6H5)3C]+[BF4]− [5]. X-ray crystallography shows both Mn2(CO)10 and Cr2(NO)2(CO)8 to have analogous unbridged structures with all of the CO and NO ligands in terminal positions and a formal metal–metal single bond joining two halves of the molecule (Figure 1) [5,6,7,8]. The metal atoms in Mn2(CO)10 and Cr2(NO)2(CO)8, all have the favored 18-electron configuration.
Decarbonylation of Mn2(CO)10 and Cr2(NO)2(CO)8 might be expected to give unsaturated structures requiring metal–metal multiple bonds, four-electron donor bridging η2-µ-CO groups, and/or five-electron donor η2-µ-NO groups to maintain the favored 18-electron configuration for all of the metal atoms. No such unsaturated Mn2(CO)n or Cr2(NO)2(CO)n−2 (n < 10) derivatives are known as stable species. Matrix isolation spectroscopic studies on photolysis products of the more extensively studied Mn2(CO)10 suggest structures with a four-electron donor bridging η2-µ-CO group for Mn2(CO)9 and an unbridged structure with a short Mn≡Mn formal triple bond distance for Mn2(CO)8 (Figure 2) [9,10,11,12]. Such results are consistent with the theoretical studies on the Mn2(CO)n (n = 9, 8) systems [13]. However, theoretical studies on the unsaturated Cr2(NO)2(CO)n (n = 7, 6) systems [14] suggest very different low-energy structures than those found for the isoelectronic Mn2(CO)n+2 derivatives (Figure 2). Thus the lowest energy Cr2(NO)2(CO)7 structure is an unbridged structure with a Cr=Cr distance suggesting the formal double bond required to preserve the 18-electron configuration for both chromium atoms. However, the lowest energy structures of the more highly unsaturated Cr(NO)2(CO)6 are doubly bridged structures with short Cr≡Cr distances suggesting formal triple bonds, again preserving the 18-electron configuration for the chromium atoms.
In view of the different types of low-energy structures predicted for isoelectronic unsaturated Mn2(CO)n and Cr2(NO)2(CO)n−2 derivatives, investigation of the intermediate isoelectronic heterobinuclear derivatives CrMn(NO)(CO)n−1 is of interest. The saturated heterobinuclear CrMn(NO)(CO)9 has not yet been reported, although the heterobinuclear metal carbonyl anion [CrMn(CO)9L]− (L = CO, PR3) is known [15,16,17,18,19]. However, CrMn(NO)(CO)9 is potentially accessible from the metathesis of the known Cr(NO)(CO)4− anion with the manganese carbonyl halides Mn(CO)5X (X = Cl, Br, I) or the known Mn(CO)5− anion with Cr(CO)4(NO)X (X = Cl, Br, I). Analogous reactions have been used to synthesize the mixed metal carbonyl derivatives ReMn(CO)10 and ReCo(CO)9 [20]. This paper discusses theoretical studies on the CrMn(NO)(CO)9 and CrMn(NO)(CO)8 systems, isoelectronic with the stable Mn2(CO)10 and Mn2(CO)9, respectively.

2. Theoretical Methods

Electron correlation effects were considered using the density functional theory (DFT) methods. The first two DFT approaches employed herein were same as those in previous work on the Mn2(CO)n system, i.e., the B3LYP and BP86 functionals [13]. The B3LYP functional is an HF/DFT hybrid method using Becke’s three-parameter functional (B3) [21] and the Lee-Yang-Parr generalized gradient correlation functional (LYP) [22], whereas the BP86 functional is a pure DFT method combining Becke’s 1988 exchange functional (B) [23] with Perdew’s 1986 gradient correlation functional (P86) [24]. In conjunction with the B3LYP and BP86 functionals, all-electron double zeta plus polarization (DZP) basis sets were used. For carbon, nitrogen, and oxygen atoms, the DZP basis sets begin with Dunning’s standard double zeta contraction [25] of Huzinaga’s primitive sets (DZ) [26] and add one set of pure spherical harmonic d functions with orbital exponents αd(C) = 0.75, αd(N) = 0.80 and αd(O) = 0.85. The contraction scheme for the carbon, nitrogen, and oxygen basis sets is (9s5p1d/4s2p1d). For chromium and manganese atoms, the DZP basis sets, designated as (14s11p6d/10s8p3d), use the Wachters’ primitive set [27] augmented by two sets of p functions and one set of d functions and contracted following Hood et al. [28]. For CrMn(NO)(CO)9, there are 398 contracted Gaussian functions with the present DZP basis set.
In addition to the B3LYP and BP86 functionals, a newer generation functional, M06-L, was employed. The M06-L functional uses a meta-GGA functional proposed by Zhao and Truhlar [29], and has been reported to give better overall performance for organometallic compounds than previously used functionals [30,31]. The correlation-consistent polarized valence triple-ζ (cc-pVTZ) basis sets were used for the M06-L computations. The cc-pVTZ basis sets for carbon, nitrogen, and oxygen atoms are given by Dunning [32], while those for chromium and manganese atoms come from Balabanov and Peterson [33]. With the cc-pVTZ basis sets, the basis functions for CrMn(NO)(CO)9 increase to 736.
Conceivable structures of CrMn(NO)(CO)n (n = 9, 8) were fully optimized at the B3LYP/DZP, BP86/DZP, and M06-L/cc-pVTZ levels of theory. Harmonic vibrational frequencies were also calculated at the same levels by evaluating analytically the second derivatives of the energy with respect to the nuclear coordinates. All of the B3LYP/DZP and BP86/DZP computations were carried out with the Gaussian 03 program [34] in which the fine grid (75, 302) was the default for evaluating the integrals numerically. All of the M06-L/cc-pVTZ computations were carried out utilizing the Gaussian 09 program [35] with an ultrafine grid (99, 590) for numerical integration. The three DFT methods generally predict similar results in the present work, so we discuss mainly the M06-L results in the text, except as otherwise indicated. The optimized geometries from the M06-L/cc-pVTZ computations are depicted in Figure 3 and Figure 4 with all bond distances given in angstroms, while Table 1 lists their electronic states and energies. All of the B3LYP and BP86 results are listed in the Supplementary Materials.

3. Results and Discussion

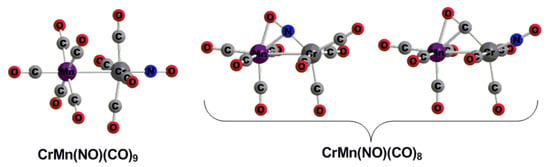
3.1. CrMn(NO)(CO)9

Since it was discovered in 1954 [1], dimanganese decacarbonyl Mn2(CO)10 has been studied extensively [2,3,4,6,7,8,9,10,11,12,36,37,38,39,40,41,42,43,44]. The following three structures were studied for Mn2(CO)10 [13]:
(1)
The staggered (OC)5Mn-Mn(CO)5 structure with D4d symmetry, which is the global minimum;
(2)
The eclipsed (OC)5Mn-Mn(CO)5 structure with D4h symmetry, which is a transition state with a small imaginary vibrational frequency and somewhat higher energy;
(3)
The doubly bridged (OC)4Mn(μ-CO)2Mn(CO)4 structure with D2h symmetry, like the global minimum of Cr2(CO)10 [45], which is also a transition state and has much higher energy.
Replacing one MnCO unit in the above three Mn2(CO)10 structures by an isoelectronic CrNO unit gives seven possible CrMn(NO)(CO)9 structures. Optimizing these seven starting structures gives only three CrMn(NO)(CO)9 minima, i.e., 9-1S, 9-2S, and 9-3S (Figure 3 and Table 1).
The CrMn(NO)(CO)9 structures 9-1S and 9-2S are very similar with staggered unbridged (OC)5Mn-Cr(CO)4(NO) conformations, corresponding to the staggered (OC)5Mn-Mn(CO)5 structure (Figure 3). They differ only in the positions of the nitrosyl group. The C4v structure 9-1S with an axial NO group was found to be the lowest energy structure with all real vibrational frequencies. The Cr–Mn distance in 9-1S of 2.987 Å is similar to the metal–metal bond distances of the isoelectronic Mn2(CO)10 [13] and [Cr2(CO)10]2− [45,46], suggesting a single bond thereby giving each metal atom the favored 18-electron configuration. The Cr–Mn distance of 2.961 Å in the Cs CrMn(NO)(CO)9 structure 9-2S, lying 5.8 kcal/mol in energy above 9-1S, and with an equatorial NO group is similar to that in 9-1S also suggesting a single bond.
We also optimized two eclipsed (OC)5Mn-Cr(CO)4(NO) structures, corresponding to the eclipsed (OC)5Mn-Mn(CO)5 structure. However, they both were found to be in transition states with small imaginary vibrational frequencies. The corresponding normal mode is related to the inner rotation around the Cr–Mn bond and leads to the corresponding staggered structures, i.e., 9-1S or 9-2S.
The third CrMn(NO)(CO)9 structure, namely the Cs structure 9-3S lying 20.2 kcal/mol above the global minimum 9-1S, has one bridging nitrosyl and one semibridging carbonyl, similar to the doubly bridged (OC)4Mn(μ-CO)2Mn(CO)4 structure [13] and the global minimum of Cr2(CO)10 [45]. The nitrosyl bridge in 9-3S is nearly symmetrical with a Cr–N distance of 2.059 Å and an Mn–N distance of 1.905 Å. However, the CO bridge in 9-3S is actually a very weak semibridge bonded mainly to the chromium atom with a Cr–C distance of 1.928 Å with a long Mn–C distance of 2.658 Å. The Cr–Mn distance of 2.871 Å in 9-3S is shorter than the Cr–Mn bonds in 9-1S and 9-2S, but still can be interpreted as a formal single bond, which, however, is shortened by the NO and CO bridges. Structure 9-3S has all real vibrational frequencies with both B3LYP and BP86 methods, indicating a genuine minimum. However, the M06-L method predicts a tiny imaginary frequency of 2i cm−1 for 9-3S, which may be an artifact arising from numerical integration errors.

3.2. CrMn(NO)(CO)8

We have found 12 stationary points for the CrMn(NO)(CO)8 stoichiometry, corresponding to the three kinds of previously studied [13] structures for Mn2(CO)9, namely (a) the singly bridged (OC)4Mn(η2-µ-CO)Mn(CO)4 structures, (b) the unbridged (OC)5Mn-Mn(CO)4 structures, and (c) the triply bridged (OC)3Mn(μ-CO)3Mn(CO)3 structures (Figure 4 and Table 1) [13]. The Cs singly nitrosyl-bridged structure (OC)4Mn(μ-NO)Cr(CO)4 8-1S has the lowest energy and all real harmonic vibrational frequencies, suggesting it to be the global minimum of CrMn(NO)(CO)8. In 8-1S, the short Mn–O distance of 2.104 Å to the bridging NO group suggests a five-electron donor bridging η2-µ-NO group. The Cr–Mn distance in 8-1S of 2.937 Å, which is similar to that in 9-1S, corresponds to the single bond required by the 18-electron rule if the bridging NO group is a five-electron donor.
Similar to 8-1S, the CrMn(NO)(CO)8 structures 8-2S, 8-4S, and 8-7S also have singly bridged architectures, but with their NO groups as a terminal ligand bonded to the chromium atom with a carbonyl group bridging the Cr–Mn bond (Figure 4). Structures 8-2S, 8-4S, and 8-7S, lying 1.1, 3.6, and 7.4 kcal/mol, respectively, in energy above 8-1S (Table 1) are all genuine minima with all real harmonic vibrational frequencies. The Cr–Mn distances in 8-2S, 8-4S, and 8-7S of 2.88 to 2.94 Å, correspond to single bonds. The Mn–O distances to the bridging CO group in 8-2S, 8-4S, and 8-7S of 2.20 to 2.23 Å indicate four-electron donor µ-η2-CO bridging carbonyl groups thereby giving the favored 18-electron configuration to all metal atoms. The four CrMn(NO)(CO)8 structures 8-1S, 8-2S, 8-4S, and 8-7S with a five-electron donor bridging η2-µ-NO group or a four-electron donor bridging η2-µ-CO group are related to the lowest energy Mn2(CO)9 structure which has a four-electron donor CO group and an Mn–Mn distance of ~2.9 Å [13].
The two Cs unbridged CrMn(NO)(CO)8 structures 8-3S and 8-8S, lie 3.5 and 8.2 kcal/mol, respectively, above 8-1S (Figure 4 and Table 1). The Cr-Mn distances in 8-3S and 8-8S of 2.85 to 2.88 Å are similar to that in 8-1S, suggesting formal single bonds thereby giving each structure an 18-electron configuration for one metal atom and a 16-electron configuration for the other metal atom. The 16-electron configuration is indicated by a vacant coordination site nearly perpendicular to the Cr–Mn bond. In 8-3S the chromium atom has the vacant coordination site and thus the 16-electron configuration. However, in 8-8S the manganese atom has the vacant coordination site and thus the 16-electron configuration. Structures 8-3S and 8-8S can be derived from the lowest-energy CrMn(NO)(CO)9 structure 9-1S by removing an equatorial carbonyl group. Structures 8-3S and 8-8S are genuine minima with all real harmonic vibrational frequencies with both the B3LYP and M06-L methods. However, the BP86 method computes a very small imaginary frequency of 9i cm−1 for 8-3S or 3i cm−1 for 8-8S. These very small imaginary frequencies might be considered as arising from numerical integration errors.
We originally guessed Cr=Mn double bonds in 8-3S and 8-8S since there were no vacant coordination sites at the chromium and/or manganese atoms based on the B3LYP and BP86 minima (see Figure S2 in the Supplementary Materials). However, the M06-L results clearly display a vacant coordination site at the chromium atom (in 8-3S) or the manganese atom (in 8-8S), so the Cr–Mn single bonds assigned above should be more reasonable.
The Cs unbridged CrMn(NO)(CO)8 structure 8-5S, lying 6.4 kcal/mol above 8-1S, has a Cr=Mn distance of 2.689 Å, which is ~0.3 Å shorter than that in 8-1S (Figure 4 and Table 1). This is clearly consistent with the formal Cr=Mn double bond needed to give each metal atom the favored 18-electron configuration with a positive charge on the manganese atom and a negative charge on the chromium atom. The CrMn(NO)(CO)8 structure 8-5S is related to the two lowest energy Cr2(NO)2(CO)7 structures which have exclusively terminal ligands and Cr=Cr distances of ~2.7 Å [14].
The two Cs triply bridged CrMn(NO)(CO)8 structures 8-6S and 8-10S have one normal bridging nitrosyl or carbonyl groups and two semibridging carbonyl groups (Figure 4). Structures 8-6S and 8-10S lie 6.5 and 11.5 kcal/mol, respectively, above 8-1S (Table 1). The relatively short Cr=Mn distances ~2.53 Å in these triply bridged species can be interpreted as the formal double bonds required to give each metal atom the favored 18-electron configuration. These Cr=Mn double bond distances are shortened by the three bridging CO and NO groups.
The CrMn(NO)(CO)8 structure 8-9S, lying 11.4 kcal/mol above 8-1S, has three weakly semibridging carbonyl groups (Figure 4 and Table 1). Two of these semibridging carbonyl groups have long Mn–C distances of 2.59 to 2.71 Å whereas the third has a long Cr–C distance of 2.69 Å as shown by dashed lines in Figure 4. This indicates that 8-9S has a stereochemistry between that of unbridged (OC)4Mn-Cr(CO)4(NO) and triply bridged (OC)3Mn(μ-CO)3Cr(CO)2(NO).
The Cs unbridged CrMn(NO)(CO)8 structures 8-11S and 8-12S are high-energy structures, lying 17.8 and 21.6 kcal/mol, respectively, in energy above 8-1S (Figure 4 and Table 1). Both 8-11S and 8-12S structures have Cr–Mn distances of ~2.95 Å suggesting formal single bonds. Structures 8-11S and 8-12S can be derived from the lowest-energy CrMn(NO)(CO)9 structure 9-2S by removing an axial carbonyl group.

3.3. The Cr–Mn Wiberg Bond Indices Given by Natural Bond Orbital Analysis

Wiberg bond indices (WBIs) for the chromium-manganese interactions in the optimized CrMn(NO)(CO)n (n = 9, 8) structures were determined using the Weinhold’s NBO analysis, and are shown in Table 2. For metal–metal bonds involving d-block transition metals, the WBI values are only 10 to 30% of the formal bond order in singlet structures. For example, a WBI of only 0.11 was found for the formal Fe–Fe single bond in triply CO-bridged Fe2(CO)9 structure [47]. The WBI values for the analogous formal Cr–Mn single bonds in the CrMn(NO)(CO)n (n = 9, 8) structures range from 0.11 to 0.15. The WBIs for the formal Cr=Mn double bonds in CrMn(NO)(CO)8 structures 8-5S, 8-6S, 8-9S, and 8-10S range from 0.18 to 0.26, which are roughly twice of those for the Cr–Mn single bonds. Generally, the WBI values are consistent with the bond orders assigned based on the chromium–manganese distances.

3.4. Vibrational Frequencies

The predicted ν(CO) and ν(NO) stretching frequencies for the lowest energy structures of CrMn(NO)(CO)n (n = 9, 8) are very useful in detecting such species in future experimental work. Table 3 summarizes our theoretical ν(CO) and ν(NO) frequencies for the CrMn(NO)(CO)n (n = 9, 8) structures using the BP86 functional. Though these frequencies were also calculated using the B3LYP and M06-L methods, the BP86 method has been shown to give ν(CO) frequencies closer to the experimental values without using any scaling factors than the B3LYP method [48,49]. The M06-L method gives similar ν(CO) and ν(NO) frequencies for the CrMn(NO)(CO)n (n = 9, 8) structures to the B3LYP method (see Tables S2 and S3 in the Supplementary Materials).
The data in Table 3 indicate that genuine terminal ν(CO) frequencies fall in the range 1939 to 2082 cm−1 similar to other metal carbonyl derivatives. If the terminal ν(CO) group is weakly bonded in a semibridging manner to the other transition metal atom, such as those in structures 9-3S, 8-6S, 8-9S, and 8-10S, then this ν(CO) frequency can be somewhat lower with the ν(CO) frequency of 1923 cm−1 in 9-3S being the lowest such ν(CO) frequency among the CrMn(NO)(CO)n structures discussed in this work. The ν(CO) frequencies for bridging carbonyl groups are significantly lower than the ν(CO) frequencies for terminal carbonyl groups in otherwise similar structures as is generally found for metal carbonyl derivatives. Thus the ν(CO) frequency for the two-electron donor bridging carbonyl group in 8-10S is 1853 cm−1. The ν(CO) frequencies for four-electron donor η2-µ-CO carbonyl groups are even lower than those for two-electron donor carbonyl groups. Thus the ν(CO) frequencies for the four-electron donor η2-µ-CO groups are in 8-2S, 8-4S, and 8-7S range from 1739 to 1756 cm−1.
The terminal ν(NO) frequencies for the CrMn(NO)(CO)n (n = 9, 8) structures are predicted to occur at 1775 to 1810 cm−1 (Table 3). The ν(NO) frequencies for three-electron donor bridging nitrosyls in the CrMn(NO)(CO)n structures are predicted to occur at 1595 to 1618 cm−1. Similar to four-electron donor η2-µ-CO carbonyl group, the five-electron donor η2-µ-NO nitrosyl group in 8-1S is predicted to exhibit a ν(NO) frequency of 1511 cm−1 which is lower than those of the three-electron donor bridging NO groups. Thus a five-electron donor nitrosyl group can also be recognized by its abnormally low ν(NO) frequency.

3.5. Carbonyl Dissociation Energies

The bond dissociation energies for the loss of one carbonyl group from the CrMn(NO)(CO)9 global minimum 9-1S is 25.7 kcal/mol (B3LYP), 35.0 kcal/mol (BP86), or 37.1 kcal/mol (M06-L). This carbonyl dissociation energy is in approximate agreement with the experimental [50] carbonyl dissociation energies of 27 kcal/mol for Ni(CO)4 or 37 kcal/mol for Cr(CO)6. However, it is significantly lower than the experimental carbonyl dissociation energy of 41 kcal/mol for Fe(CO)5.

4. Conclusions

The lowest energy CrMn(NO)(CO)9 structures 9-1S and 9-2S have staggered unbridged configurations with octahedral coordination of each metal atom counting the metal–metal bond. Related structures are found by X-ray crystallography for the homometallic analogues Cr2(NO)2(CO)8 and Mn2(CO)10, which are also computed to be the lowest energy structures. In the lowest energy CrMn(NO)(CO)9 and Cr2(NO)2(CO)8 structures the nitrosyl group(s) are located in axial positions trans to the metal–metal bonds. The higher energy staggered unbridged CrMn(NO)(CO)9 isomer 9-2S has the nitrosyl group bonded to the chromium atom in an equatorial position, i.e., cis to the Cr–Mn bond.
Both Mn2(CO)10 and Cr2(NO)2(CO)8 have significantly higher energy doubly bridged isomers lying ~20 kcal/mol above the lowest energy isomers, namely the staggered unbridged structures. For the lowest energy doubly bridged Cr2(NO)2(CO)8 structure, albeit a high-energy structure relative to the unbridged isomers, both bridging groups are nitrosyl groups suggesting preference for nitrosyl rather than carbonyl bridges in such nitrosyl carbonyl systems. In this connection, the lowest energy bridged CrMn(NO)(CO)9 structure 9-3S has a nearly symmetrical nitrosyl bridge within ~0.1 Å but only a very weakly semibridging carbonyl group.
The lowest energy Mn2(CO)9 structure has a four-electron donor bridging η2-µ-CO group with an Mn–O bond as well as Mn–C bonds in addition to eight terminal carbonyl groups (Figure 2). The three lowest-energy CrMn(NO)(CO)8 structures 8-1S, 8-2S, and 8-4S are of this general type. However, the lowest energy among these three CrMn(NO)(CO)8 structures, namely 8-1S, the bridging group is a five-electron donor η2-µ-NO group with an Mn–O bond as well as two M–N (M = Mn, Cr) bonds. In the other two of these CrMn(NO)(CO)8 structures, namely 8-2S and 8-4S, the bridging group is a four-electron donor η2-µ-CO group similar to that in the lowest energy Mn2(CO)9 structure.
Low-energy Cr2(NO)2(CO)7 structures with bridging four-electron donor η2-µ-CO groups or five-electron donor η2-µ-NO groups were not found in the previous theoretical study [14]. Instead the only two Cr2(NO)2(CO)7 structures having energies found within ~10 kcal/mol of the global minimum have exclusively terminal CO and NO groups and Cr=Cr distances of ~2.8 Å interpreted as the formal double bonds required to give each chromium atom the favored 18-electron configuration. The CrMn(NO)(CO)8 structure 8-5S is of this type with similar Cr=Mn distance of 2.7 Å. A related Mn2(CO)9 structure with exclusively terminal carbonyl groups and an Mn=Mn distance of ~2.74 Å is found to lie ~6 kcal/mol in energy above the Mn2(CO)8(η2-µ-CO) lowest energy isomer [13].

Supplementary Materials

The following are available online at https://www.mdpi.com/2304-6740/7/10/127/s1. Figure S1. The three optimized CrMn(NO)(CO)9 structures at B3LYP/DZP and BP86/DZP levels. Figure S2. The 12 optimized CrMn(NO)(CO)8 structures at B3LYP/DZP and BP86/DZP levels. Table S1: Relative energies and Cr–Mn distances for the optimized CrMn(NO)(CO)n (n = 9, 8) structures at B3LYP/DZP, BP86/DZP, and M06-L/cc-pVTZ levels. Tables S2 and S3: The vibrational frequencies for the isomers of CrMn(NO)(CO)n (n = 9, 8) at B3LYP/DZP, BP86/DZP, and M06-L/cc-pVTZ levels. Tables S4 and S5: The Cartesian coordinates of the optimized CrMn(NO)(CO)n (n = 9, 8) isomers at B3LYP/DZP, BP86/DZP, and M06-L/cc-pVTZ levels. Complete Gaussian 03 and Gaussian 09 references.

Author Contributions

G.L.: Performed research, analyzed data, and wrote the draft of the paper; L.W.: Performed M06-L computations, collected the data, and revised the figures and tables accordingly; R.B.K.: Conceived of the study, designed research, analyzed data, and wrote the final paper.

Funding

This research received no external funding.

Acknowledgments

G.L. thanks the University of Georgia for a visiting professorship during 2014–2015. R.B.K. acknowledges private discussions several years ago with Thomas Bitterwolf (University of Idaho) that led to this project.

Conflicts of Interest

The authors declare no conflict of interests.

References

  1. Brimm, E.O.; Lynch, M.A.; Sesny, W.J. Preparation and properties of manganese carbonyl. J. Am. Chem. Soc. 1954, 76, 3831–3835. [Google Scholar] [CrossRef]
  2. Closson, R.D.; Buzbee, L.R.; Ecke, G.C. A new metal carbonyl synthesis. J. Am. Chem. Soc. 1958, 80, 6167–6170. [Google Scholar] [CrossRef]
  3. Podall, H.E.; Dunn, J.H.; Shapiro, H. Reductive carbonylation synthesis of metal carbonyls. II. Synthesis of manganese carbonyl and group VI-B metal carbonyls by the alkylaluminum method. J. Am. Chem. Soc. 1960, 82, 1325–1330. [Google Scholar] [CrossRef]
  4. King, R.B.; Stokes, J.C.; Korenowski, T.F. A convenient synthesis of dimanganese decarbonyl from inexpensive starting materials at atmospheric pressure. J. Organometal. Chem. 1968, 11, 641–643. [Google Scholar] [CrossRef]
  5. Masters, A.P.; Parvez, M.; Sorensen, T. Preparation of Cr2(CO)8(NO)2 and X-ray crystal structures of Cr2(CO)8(NO)2 and Cr2(CO)9NO−. Stereochemical comparisons to Cr2(CO)102−. Can. J. Chem. 1991, 69, 2136–2141. [Google Scholar] [CrossRef]
  6. Dahl, L.F.; Ishishi, E.; Rundle, R.E. Polynuclear metal carbonyls. I. Structures of Mn2(CO)10 and Re2(CO)10. J. Chem. Phys. 1957, 26, 1750–1751. [Google Scholar] [CrossRef]
  7. Almenningen, A.; Jacobsen, G.G.; Seip, H.M. On the molecular structure of dimanganese decacarbonyl Mn2(CO)10. Acta Chem. Scand. 1969, 23, 685–686. [Google Scholar] [CrossRef]
  8. Churchill, M.R.; Amoh, K.N.; Wasserman, H.J. Redetermination of the crystal structure of dimanganese decacarbonyl and determination of the crystal structure of dirhenium decacarbonyl. Revised values for the manganese–manganese and rhenium–rhenium bond lengths in dimanganese decacarbonyl and dirhenium decacarbonyl. Inorg. Chem. 1981, 20, 1609–1611. [Google Scholar]
  9. Hepp, A.F.; Wrighton, M.S. Relative importance of metal–metal bond scission and loss of carbon monoxide from photoexcited dimanganese decacarbonyl: Spectroscopic detection of a coordinatively unsaturated, carbonyl-bridged dinuclear species in low-temperature alkane matrices. J. Am. Chem. Soc. 1983, 105, 5934–5935. [Google Scholar] [CrossRef]
  10. Kvietok, F.A.; Bursten, B.E. Matrix photochemistry of Mn2(CO)10: Reversible formation of Mn2(CO)8 from Mn2(CO)8(μ-η1:η2-CO). Organometallics 1995, 14, 2395–2399. [Google Scholar] [CrossRef]
  11. Dunkin, I.R.; Härter, P.; Shields, C.J. Recognition of a semibridging carbonyl group in dimanganese nonacarbonyl from plane-polarized photolysis of dimanganese decacarbonyl in argon matrixes at 12 K. J. Am. Chem. Soc. 1984, 106, 7248–7249. [Google Scholar] [CrossRef]
  12. Church, S.P.; Hermann, H.; Grevels, F.W. The primary photoproducts of Mn2(CO)10: Direct I.R. observation and decay kinetics of Mn(CO)5 and Mn2(CO)9 in hydrocarbon solution at room temperature. Chem. Commun. 1984, 12, 785–786. [Google Scholar] [CrossRef]
  13. Xie, Y.; Jang, J.H.; King, R.B.; Schaefer, H.F. Binuclear homoleptic manganese carbonyls: Mn2(CO)x (x = 10, 9, 8, 7). Inorg. Chem. 2003, 42, 5219–5230. [Google Scholar] [CrossRef] [PubMed]
  14. Wang, H.; Xie, Y.; Zhang, J.D.; King, R.B.; Schaefer, H.F. Chromium carbonyl nitrosyls: Comparison with isoelectronic manganese carbonyl derivatives. Inorg. Chem. 2007, 46, 1836–1846. [Google Scholar] [CrossRef] [PubMed]
  15. Anders, U.; Graham, W.A.G. Organometallic compounds with metal–metal bonds. VI. Preparation and infrared spectra of the carbonylmetalate ions [(OC)5M-M′(CO)5]− (M = Mn, Re; M′ = Cr, Mo, W). J. Am. Chem. Soc. 1967, 89, 539–541. [Google Scholar] [CrossRef]
  16. Ruff, J.K. The chemistry of the dinuelear carbonyl anions. II. Mixed-metal derivatives. Inorg. Chem. 1968, 7, 1818–1821. [Google Scholar] [CrossRef]
  17. Park, Y.K.; Kim, S.J.; Kim, J.H.; Han, I.S.; Lee, C.H. Kinetic studies of the cleavage of M+[M′M″(CO)9L]− (M+ = Na+, PPN+; M′ = Cr, W.; M″ = Mn, Re; L = CO, PR3). J. Organomet. Chem. 1991, 408, 193–202. [Google Scholar] [CrossRef]
  18. Park, Y.K.; Han, I.S.; Kim, J.S.; Lee, C.J.; Baek, Y.O.; Song, G.O. Kinetic studies on the reactions of the heterobimetallic anion (OC)5CrMn(CO)5−M+ (M+ = Na+, PPN+) with CH3I. Bull. Korean Chem. Soc. 1994, 15, 537–541. [Google Scholar]
  19. Park, Y.K.; Kim, G.S.; Song, G.O. Kinetic studies on the reactions of the heterobimetallic anion (OC)5CrMn(CO)5−M+ (M+ = Na+, PPN+) with allyl bromide. Bull. Korean Chem. Soc. 1995, 16, 310–315. [Google Scholar]
  20. Kruck, T.; Höfler, M.; Noack, M. Reaktionsweisen von Rhenium(I)-Kohlenoxidkomplexen und neue Anschauungen über den Mechanismus der Basenreaktion von Metallcarbonylen. Chem. Ber. 1966, 99, 1153–1167. [Google Scholar] [CrossRef]
  21. Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
  22. Lee, C.; Yang, W.T.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  23. Becke, A.D. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A 1988, 38, 3098–3100. [Google Scholar] [CrossRef] [PubMed]
  24. Perdew, J.P. Density-functional approximation for the correlation energy of the inhomogeneous electron gas. Phys. Rev. B 1986, 33, 8822–8824. [Google Scholar] [CrossRef]
  25. Dunning, T.H., Jr. Gaussian basis functions for use in molecular calculations. I. Contraction of (9s5p) atomic basis sets for the first-row atoms. J. Chem. Phys. 1970, 53, 2823–2833. [Google Scholar] [CrossRef]
  26. Huzinaga, S. Gaussian-type functions for polyatomic systems. I. J. Chem. Phys. 1965, 42, 1293–1302. [Google Scholar] [CrossRef]
  27. Wachters, A.J.H. Gaussian basis set for molecular wavefunctions containing third-row atoms. J. Chem. Phys. 1970, 52, 1033–1036. [Google Scholar] [CrossRef]
  28. Hood, D.M.; Pitzer, R.M.; Schaefer, H.F. Electronic structure of homoleptic transition metal hydrides: TiH4, VH4, CrH4, MnH4, FeH4, CoH4, and NiH4. J. Chem. Phys. 1979, 71, 705–712. [Google Scholar] [CrossRef]
  29. Zhao, Y.; Truhlar, D.G. A new local density functional for main-group thermochemistry, transition metal bonding, thermochemical kinetics, and noncovalent interactions. J. Chem. Phys. 2006, 125, 194101. [Google Scholar] [CrossRef] [Green Version]
  30. Zhao, Y.; Truhlar, D.G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theor. Chem. Acc. 2008, 120, 215–241. [Google Scholar]
  31. Zhao, Y.; Truhlar, D.G. Density functionals with broad applicability in chemistry. Acc. Chem. Res. 2008, 41, 157–167. [Google Scholar] [CrossRef] [PubMed]
  32. Dunning, T.H. Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen. J. Chem. Phys. 1989, 90, 1007–1023. [Google Scholar] [CrossRef]
  33. Balabanov, N.B.; Peterson, K.A. Systematically convergent basis sets for transition metals. I. All-electron correlation consistent basis sets for the 3d elements Sc–Zn. J. Chem. Phys 2005, 123, 064107. [Google Scholar] [CrossRef] [PubMed]
  34. Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Montgomery, J.A., Jr.; Vreven, T.; Kudin, K.N.; Burant, J.C.; et al. Gaussian 03, Revision D 01; Gaussian, Inc.: Wallingford, CT, USA, 2004. [Google Scholar]
  35. Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09, Revision D.01; Gaussian, Inc.: Wallingford, CT, USA, 2013. [Google Scholar]
  36. Hileman, J.C.; Huggins, D.K.; Kaesz, H.D. Derivatives of technetium carbonyl. Synthesis and properties of the carbonyl halides and the pentacarbonyl hydride. Inorg. Chem. 1962, 1, 933–938. [Google Scholar] [CrossRef]
  37. Flitcroft, N.; Huggins, D.K.; Kaesz, H.D. Infrared spectra of (CO)5Mn-Re(CO)5 and the carbonyls of manganese, technetium, and rhenium; assignment of C≡O and M=C stretching absorptions. Inorg. Chem. 1964, 3, 1123–1130. [Google Scholar] [CrossRef]
  38. Haas, H.; Sheline, R.K. Analysis of the infrared spectra of metal carbonyls. J. Chem. Phys. 1967, 47, 2996–3021. [Google Scholar] [CrossRef]
  39. Rosa, A.; Ricciarde, G.; Baerends, E.J.; Stufkens, D.J. Density functional study of ground and excited states of Mn2(CO)10. Inorg. Chem. 1995, 34, 3425–3432. [Google Scholar] [CrossRef]
  40. Rosa, A.; Ricciarde, G.; Baerends, E.J.; Stufkens, D.J. Density functional study of the photodissociation of Mn2(CO)10. Inorg. Chem. 1996, 35, 2886–2897. [Google Scholar] [CrossRef]
  41. Decker, S.A.; Donini, O.; Klobukowski, M. A contribution to the understanding of carbonyl migration in Mn2(CO)10 via the pairwise exchange mechanism. J. Phys. Chem. A 1997, 101, 8734–8740. [Google Scholar] [CrossRef]
  42. Liddell, M.J. Organometallic clusters: What is an appropriate DFT treatment? J. Organomet. Chem. 1998, 565, 271–277. [Google Scholar] [CrossRef]
  43. van Gisbergen, S.J.A.; Groeneveld, J.A.; Rosa, A.; Snijders, J.G.; Baerends, E.J. Excitation energies for transition metal compounds from time-dependent density functional theory. Applications to MnO4−, Ni(CO)4, and Mn2(CO)10. J. Phys. Chem. A 1999, 103, 6835–6844. [Google Scholar] [CrossRef]
  44. Barchholtz, T.A.; Bursten, B.E. Density functional calculations of dinuclear organometallic carbonyl complexes. Part I: Metal–metal and metal–CO bond energies. J. Organomet. Chem. 2000, 596, 212–220. [Google Scholar]
  45. Li, S.; Richardson, N.R.; Xie, Y.; King, R.B.; Schaefer, H.F. The rule breaking Cr2(CO)10. A 17 electron Cr system or a Cr=Cr double bond? Faraday Discuss. 2003, 124, 315–329. [Google Scholar] [CrossRef] [PubMed]
  46. Richardson, N.R.; Xie, Y.; King, R.B.; Schaefer, H.F. Flat potential energy surface of the saturated binuclear homoleptic chromium carbonyl Cr2(CO)11 with one, two, and three bridging carbonyls: Comparison with the well-known [HCr2(CO)10]− anion and the related [(μ-H)2Cr2(CO)9]2− and [(μ-H)2Cr2(CO)8]2− dianions. J. Phys. Chem. A 2001, 105, 11134–11143. [Google Scholar]
  47. Wang, H.; Xie, Y.; King, R.B.; Schaefer, H.F. Remarkable aspects of unsaturation in trinuclear metal carbonyl clusters: The triiron species Fe3(CO)n (n = 12, 11, 10, 9). J. Am. Chem. Soc. 2006, 128, 11376–11384. [Google Scholar] [CrossRef] [PubMed]
  48. Jonas, V.; Thiel, W. Theoretical study of the vibrational spectra of the transition metal carbonyls M(CO)6 [M = Cr, Mo, W], M(CO)5 [M = Fe, Ru, Os], and M(CO)4 [M = Ni, Pd, Pt]. J. Phys. Chem. 1995, 102, 8474–8484. [Google Scholar] [CrossRef]
  49. Silaghi-Dumitrescu, I.; Bitterwolf, T.E.; King, R.B. Butterfly diradical intermediates in photochemical reactions of Fe2(CO)6(μ-S2). J. Am. Chem. Soc. 2006, 128, 5342–5343. [Google Scholar] [CrossRef]
  50. Sunderlin, L.S.; Wang, D.; Squires, R.R. Bond strengths in first-row-metal carbonyl anions. J. Am. Chem. Soc. 1993, 115, 12060–12070. [Google Scholar] [CrossRef]
Inorganics 07 00127 g001 550
Figure 1. The lowest energy and experimental structures for the isoelectronic species Mn2(CO)10 and Cr2(NO)2(CO)8.
Figure 1. The lowest energy and experimental structures for the isoelectronic species Mn2(CO)10 and Cr2(NO)2(CO)8.
Inorganics 07 00127 g001
Inorganics 07 00127 g002 550
Figure 2. Comparison of the lowest energy Mn2(CO)n and Cr2(NO)2(CO)n−2 (n = 9, 8) structures.
Figure 2. Comparison of the lowest energy Mn2(CO)n and Cr2(NO)2(CO)n−2 (n = 9, 8) structures.
Inorganics 07 00127 g002
Inorganics 07 00127 g003 550
Figure 3. The three optimized CrMn(NO)(CO)9 structures at the M06-L/cc-pVTZ level of theory.
Figure 3. The three optimized CrMn(NO)(CO)9 structures at the M06-L/cc-pVTZ level of theory.
Inorganics 07 00127 g003
Inorganics 07 00127 g004 550
Figure 4. The 12 optimized CrMn(NO)(CO)8 structures at the M06-L/cc-pVTZ level of theory.
Figure 4. The 12 optimized CrMn(NO)(CO)8 structures at the M06-L/cc-pVTZ level of theory.
Inorganics 07 00127 g004
Table
Table 1. Relative energies (ΔE, in kcal/mol) and Cr–Mn distances (in Å) for the optimized CrMn(NO)(CO)n (n = 9, 8) structures at the M06-L/cc-pVTZ level of theory.
Table 1. Relative energies (ΔE, in kcal/mol) and Cr–Mn distances (in Å) for the optimized CrMn(NO)(CO)n (n = 9, 8) structures at the M06-L/cc-pVTZ level of theory.
StructureState (Sym.)ΔECr–MnStructureState (Sym.)ΔECr–Mn
9-1S1A1 (C4v)0.02.9878-5S1A′ (Cs)6.42.689
9-2S1A′ (Cs)5.82.9618-6S1A′ (Cs)6.52.531
9-3S1A′ (Cs)20.22.8718-7S1A (C1)7.42.879
8-8S1A′ (Cs)8.22.876
8-1S1A′ (Cs)0.02.9378-9S1A (C1)11.42.629
8-2S1A′ (Cs)1.12.9388-10S1A′ (Cs)11.52.531
8-3S1A′ (Cs)3.52.8458-11S1A′ (Cs)17.82.956
8-4S1A′ (Cs)3.62.9258-12S1A′ (Cs)21.62.951
Table
Table 2. The Wiberg bond indices (WBIs) of the chromium–manganese bonds by natural bond orbital (NBO) analysis for the optimized low-lying CrMn(NO)(CO)n (n = 9, 8) structures.
Table 2. The Wiberg bond indices (WBIs) of the chromium–manganese bonds by natural bond orbital (NBO) analysis for the optimized low-lying CrMn(NO)(CO)n (n = 9, 8) structures.
StructureCr–Mn (Å)Formal Bond OrderWBI (Cr–Mn)StructureCr–Mn (Å)Formal Bond OrderWBI (Cr–Mn)
9-1S2.98710.118-5S2.68920.18
9-2S2.96110.118-6S2.53120.22
9-3S2.87110.138-7S2.87910.14
8-8S2.87610.15
8-1S2.93710.128-9S2.62920.22
8-2S2.93810.148-10S2.53120.26
8-3S2.84510.158-11S2.95610.18
8-4S2.92510.148-12S2.95110.22
Table
Table 3. The ν(CO) and ν(NO) vibrational frequencies (in cm−1) and infrared intensities (in km/mol, given in parentheses) of the CrMn(NO)(CO)n (n = 9, 8) complexes at the BP86/DZP level.
Table 3. The ν(CO) and ν(NO) vibrational frequencies (in cm−1) and infrared intensities (in km/mol, given in parentheses) of the CrMn(NO)(CO)n (n = 9, 8) complexes at the BP86/DZP level.
Struct.ν(CO) *ν(NO) *
9-1S1966 (0), 1966 (0), 1983 (298), 1994 (0), 1999 (2182), 1999 (2182), 2002 (0), 2020 (819), 2082 (86)1807 (984)
9-2S1965 (5), 1970 (550), 1977 (601), 1983 (146), 1996 (2193), 2000 (1133), 2001 (37), 2021 (1285), 2078 (70)1804 (641)
9-3S1923 (371), 1961 (184), 1981 (230), 1983 (988), 1996 (2151), 1997 (740), 2003 (145), 2031 (1642), 2076 (11)1595 (363)
8-1S1954 (517), 1970 (86), 1970 (346), 1984 (869), 1995 (2232), 1996 (393), 2027 (1112), 2073 (93)1511 (397)
8-2S1742 (406), 1964 (204), 1966 (39), 1987 (463), 1999 (2207), 2000 (609), 2024 (845), 2070 (189)1803 (991)
8-3S1951 (20), 1965 (91), 1978 (1476), 1985 (320), 1988 (1127), 1993 (1058), 2011 (1039), 2068 (145)1792 (856)
8-4S1739 (499), 1966 (2), 1971 (701), 1978 (700), 1990 (107), 1995 (2296), 2026 (1184), 2067 (44)1801 (430)
8-5S1953 (250), 1962 (19), 1972 (1451), 1976 (992), 1993 (409), 1995 (309), 2004 (1818), 2065 (238)1785 (718)
8-6S1942 (476), 1944 (228), 1966 (1020), 1975 (643), 1995 (1175), 2002 (566), 2013 (1844), 2063 (133)1618 (415)
8-7S1756 (402), 1960 (128), 1974 (621), 1978 (1193), 1987 (651), 1999 (734), 2019 (1427), 2064 (180)1810 (673)
8-8S1949 (11), 1960 (67), 1972 (260), 1977 (1830), 1981 (89), 1988 (2072), 2010 (785), 2063 (60)1805 (1093)
8-9S1925 (208), 1941 (620), 1959 (97), 1970 (1165), 1978 (566), 1992 (1192), 2012 (1718), 2056 (51)1796 (753)
8-10S1853 (230), 1950 (558), 1957 (879), 1977 (959), 1993 (545), 1995 (691), 2011 (1662), 2060 (273)1775 (897)
8-11S1939 (557), 1955 (17), 1979 (384), 1987 (1996), 1987 (1448), 1999 (0), 2004 (827), 2071 (133)1779 (661)
8-12S1941 (318), 1947 (933), 1969 (556), 1985 (2029), 1986 (106), 1989 (882), 2012 (712), 2065 (66)1800 (579)
* ν in italic means semibridging CO groups; ν in bold means bridging CO or NO groups; ν in bold and underlined means four-electron CO or five-electron NO bridges.

Share and Cite

MDPI and ACS Style

Li, G.; Wen, L.; King, R.B. Heterobimetallic Chromium Manganese Carbonyl Nitrosyls: Comparison with Isoelectronic Homometallic Binuclear Chromium Carbonyl Nitrosyls and Manganese Carbonyls. Inorganics 2019, 7, 127. https://doi.org/10.3390/inorganics7100127

AMA Style

Li G, Wen L, King RB. Heterobimetallic Chromium Manganese Carbonyl Nitrosyls: Comparison with Isoelectronic Homometallic Binuclear Chromium Carbonyl Nitrosyls and Manganese Carbonyls. Inorganics. 2019; 7(10):127. https://doi.org/10.3390/inorganics7100127

Chicago/Turabian Style

Li, Guoliang, Limei Wen, and R. Bruce King. 2019. "Heterobimetallic Chromium Manganese Carbonyl Nitrosyls: Comparison with Isoelectronic Homometallic Binuclear Chromium Carbonyl Nitrosyls and Manganese Carbonyls" Inorganics 7, no. 10: 127. https://doi.org/10.3390/inorganics7100127

APA Style

Li, G., Wen, L., & King, R. B. (2019). Heterobimetallic Chromium Manganese Carbonyl Nitrosyls: Comparison with Isoelectronic Homometallic Binuclear Chromium Carbonyl Nitrosyls and Manganese Carbonyls. Inorganics, 7(10), 127. https://doi.org/10.3390/inorganics7100127

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop