Surface and Groundwater Interactions: A Review of Coupling Strategies in Detailed Domain Models
Abstract
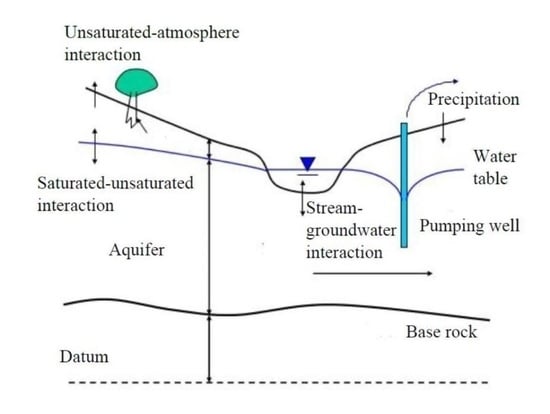
:1. Introduction
2. Detailed Domain Models
2.1. Regional Scale Modelling
2.1.1. Fully-Coupled Scheme
Governing Equations
- Porous Medium (3D) Richards’ Equation:
- Darcy–Buckingham Equation:
2.1.2. Loosely-Coupled Scheme
Governing Equations
2.2. Local Scale Modelling
2.2.1. Traditional Methodologies
2.2.2. Hierarchical Modelling Approach
3. Domain Integrated Modelling
3.1. Process-Based Models
3.2. Stochastic Models
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Vaux, H. Groundwater under stress: The importance of management. Environ. Earth Sci. 2011, 62, 19–23. [Google Scholar] [CrossRef] [Green Version]
- Zektser, I.S.; Everett, L.G. Groundwater Resources of the World and Their Use; IHP-VI, Series on groundwater n°6; UNESDOC: Paris, France, 2004. [Google Scholar]
- Lejars, C.; Daoudi, A.; Amichi, H. The key role of supply chain actors in groundwater irrigation development in North Africa. Hydrogeol. J. 2017, 25, 1593–1606. [Google Scholar] [CrossRef]
- Toran, L. Groundwater–Surface Water Interaction. In Encyclopedia of Water: Science, Technology, and Society; Maurice, P.A., Ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2019; pp. 1–12. [Google Scholar]
- Larocque, M.; Broda, S. Groundwater–surface water interactions in Canada. Can. Water Resour. J. Rev. Can. Ressour. Hydr. 2016, 41, 451–454. [Google Scholar] [CrossRef] [Green Version]
- Freeze, R.; Harlan, R. Blueprint for a physically-based, digitally-simulated hydrologic response model. J. Hydrol. 1969, 9, 237–258. [Google Scholar] [CrossRef]
- Great Lakes Science Advisory Board. Great Lakes Surface and Groundwater Model. Integration Review Literature Review, Options for Approaches and Preliminary Action Plan for the Great Lakes Basin Prepared by the Great Lakes Science Advisory Board Research Coordination Committee Submitted to rge Internation Join Commission. In Proceedings of the International Joint Commission Workshop Groundwater-Surface water modeling for the Great Lakes Basin, Ann Arbor, MI, USA, 4–5 April 2018. [Google Scholar]
- Abbott, M.B.; Bathurst, J.C.; Cunge, J.A.; O’Connell, P.E.; Rasmussen, J. An introduction to the European Hydrological System—Systeme Hydrologique Europeen, ‘SHE’, 1: History and philosophy of a physically-based, distributed modelling system. J. Hydrol. 1986, 87, 45–59. [Google Scholar] [CrossRef]
- Ewen, J.; Parkin, G.; O’Connell, P.E. SHETRAN: Distributed River Basin Flow and Transport Modeling System. J. Hydrol. Eng. 2000, 5, 250–258. [Google Scholar] [CrossRef] [Green Version]
- Abbott, M.B.; Bathurst, J.C.; Cunge, J.A.; O’Connell, P.E.; Rasmussen, J. An introduction to the European Hydrological System—Systeme Hydrologique Europeen, ‘SHE’, 2: Structure of a physically-based, distributed modelling system. J. Hydrol. 1986, 87, 61–77. [Google Scholar] [CrossRef]
- Mare, H.G.; Rademeyer, J.L.; Sami, K. Application on Groundwater/Surface water Interaction Modeling in the Schoonspruit Catchment. Available online: https://www.miya-water.com/fotos/artigos/02_application_on_groundwater_surface_water_interaction_modeling_in_the_schoonspruit_catchment_19810471915a326afa23030.pdf (accessed on 29 December 2020).
- Scibek, J.; Allen, D.M.; Cannon, A.J.; Whitfield, P.H. Groundwater-surface water interaction under scenarios of climate change using a high-resolution transient groundwater model. J. Hydrol. 2007, 333, 165–181. [Google Scholar] [CrossRef]
- Stefania, G.A.; Rotiroti, M.; Fumagalli, L.; Simonetto, F.; Capodaglio, P.; Zanotti, C.; Bonomi, T. Modeling groundwater/surface-water interactions in an Alpine valley (the Aosta Plain, NW Italy): The effect of groundwater abstraction on surface-water resources. Hydrogeol. J. 2017, 26, 147–162. [Google Scholar] [CrossRef]
- Pitz, C.F. Predicted Impacts of Climate Change on Groundwater Resources of Washington State; Ecology Publications & Forms: Washington, DC, USA, 2016. [Google Scholar]
- Rassam, D.W.; Jolly, I.; Pickett, T. Guidelines for Modelling Groundwater-Surface Water Interactions in EWater Source Towards Best Practice Model Application; eWater CRC: Bruce, Australia, 2012. [Google Scholar]
- Kumar, C.P. Modelling of Groundwater Flow and Data Requirements. Int. J. Mod. Sci. Eng. Technol. 2015, 2, 18–27. [Google Scholar]
- Kumar, C.P. Groundwater Modelling Software—Capabilities and Limitations. IOSR J. Environ. Sci. Toxicol. Food Technol. 2012, 1, 46–57. [Google Scholar] [CrossRef]
- Dahl, M.; Nilsson, B.; Langhoff, J.H.; Refsgaard, J.C. Review of classification systems and new multi-scale typology of groundwater-surface water interaction. J. Hydrol. 2007, 344, 1–16. [Google Scholar] [CrossRef]
- Winter, T.C.; Harvey, J.W.; Franke, O.L.; Alley, W.M. Ground Water and Surface Water: A Single Resource; US Geological Survey: Reston, VA, USA, 1998; Volume 10. [Google Scholar]
- Sophocleous, M. Interactions between groundwater and surface water: The state of the science. Hydrogeol. J. 2002, 10, 52–67. [Google Scholar] [CrossRef]
- Brunner, P.A.; Simmons, C.T. HydroGeoSphere: A Fully Integrated, Physically Based Hydrological Model. Ground Water 2011, 50, 170–176. [Google Scholar] [CrossRef] [Green Version]
- Loague, K.; Heppner, C.S.; Mirus, B.B.; Ebel, B.A.; Ran, Q.; Carr, A.E.; Beville, S.H.; VanderKwaak, J.E. Physics-based hydrologic-response simulation: Foundation for hydroecology and hydrogeomorphology. Hydrol. Process. 2006, 20, 1231–1237. [Google Scholar] [CrossRef]
- Therrien, R.; McLaren, R.G.; Sudicky, E.A.; Panday, S.M. HydroGeoSphere. A Three-Dimensional Numerical Model Describing Fully-Integrated Subsurface and Surface Flow and Solute Transport; Groundwater Simulations Group, University of Waterloo: Waterloo, ON, Canada, 2010; p. 457. [Google Scholar]
- Ganji, A.; Sushama, L. Improved representation of surface-groundwater interaction in the Canadian land surface scheme. Int. J. Clim. 2018, 38, 5077–5094. [Google Scholar] [CrossRef]
- Maxwell, R.M.; Putti, M.; Meyerhoff, S.B.; Delfs, J.-O.; Ferguson, I.M.; Ivanov, V.Y.; Kim, J.; Kolditz, O.G.; Kollet, S.J.; Kumar, M.; et al. Surface-subsurface model intercomparison: A first set of benchmark results to diagnose integrated hydrology and feedbacks. Water Resour. Res. 2014, 50, 1531–1549. [Google Scholar] [CrossRef] [Green Version]
- Maxwell, R.M.; Condon, L.E.; Kollet, S.J. A high-resolution simulation of groundwater and surface water over most of the continental US with the integrated hydrologic model ParFlow v3. Geosci. Model. Dev. 2015, 8, 923–937. [Google Scholar] [CrossRef] [Green Version]
- Liggett, J.E.; Werner, A.D.; Simmons, C.T. Influence of the first-order exchange coefficient on simulation of coupled surface-subsurface flow. J. Hydrol. 2012, 414–415, 503–515. [Google Scholar] [CrossRef]
- Kollet, S.J. The integrated hydrologic model intercomparison project, IH-MIP2: A second set of benchmark results to diagnose integrated hydrology and feedbacks Stefan. Water Resour. Res. 2017, 53, 867–890. [Google Scholar] [CrossRef] [Green Version]
- Kollet, S.J.; Maxwell, R.M.; Woodward, C.S.; Smith, S.; VanderBorght, J.; Vereecken, H.; Simmer, C. Proof of concept of regional scale hydrologic simulations at hydrologic resolution utilizing massively parallel computer resources. Water Resour. Res. 2010, 46, 1–7. [Google Scholar] [CrossRef]
- Maxwell, R.M. ParFlow User’s Manual. Ground Water 2010, 1, 129. [Google Scholar]
- Kollet, S.J.; Maxwell, R.M. Integrated surface–groundwater flow modeling: A free-surface overland flow boundary condition in a parallel groundwater flow model. Adv. Water Resour. 2006, 29, 945–958. [Google Scholar] [CrossRef] [Green Version]
- Camporese, M.; Paniconi, C.; Putti, M.; Orlandini, S. Surface-subsurface flow modeling with path-based runoff routing, boundary condition-based coupling, and assimilation of multisource observation data. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef] [Green Version]
- Furman, A. Modeling Coupled Surface-Subsurface Flow Processes: A Review. Vadose Zone J. 2008, 7, 741–756. [Google Scholar] [CrossRef] [Green Version]
- Barthel, R.; Banzhaf, S. Groundwater and Surface Water Interaction at the Regional-scale – A Review with Focus on Regional Integrated Models. Water Resour. Manag. 2016, 30, 1–32. [Google Scholar] [CrossRef] [Green Version]
- Seo, S.B.; Mahinthakumar, G.; Sankarasubramanian, A.; Kumar, M. Conjunctive management of surface water and groundwater resources under drought conditions using a fully coupled hydrological model. J. Water Resour. Plan. Manag. 2018, 144, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Arena, C.; Mazzola, M.R.; Scordo, G. A simulation/optimization model for selecting infrastructure alternatives in complex water resource systems. Water Sci. Technol. 2010, 61, 3050–3060. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Giacomoni, M.H.; Joseph, J. Multi-Objective Evolutionary Optimization and Monte Carlo Simulation for Placement of Low Impact Development in the Catchment Scale. J. Water Resour. Plan. Manag. 2017, 143, 04017053. [Google Scholar] [CrossRef]
- Katsifarakis, K.; Petala, Z. Combining genetic algorithms and boundary elements to optimize coastal aquifers’ management. J. Hydrol. 2006, 327, 200–207. [Google Scholar] [CrossRef]
- Lund, J.R. Optimization modeling in water resource systems and markets. Water Trading Glob. Water Scarcity 2012, 341–353. [Google Scholar] [CrossRef]
- Mantoglou, A.; Papantoniou, M.; Giannoulopoulos, P. Management of coastal aquifers based on nonlinear optimization and evolutionary algorithms. J. Hydrol. 2004, 297, 209–228. [Google Scholar] [CrossRef]
- Rao, S.V.N.; Bhallamudi, S.M.; Thandaveswara, B.S.; Mishra, G.C. Conjunctive use of surface and groundwater for coastal and deltaic systems. J. Water Resour. Plan. Manag. 2004, 130, 255–267. [Google Scholar] [CrossRef] [Green Version]
- Safavi, H.R.; Darzi, F.; Mariño, M.A. Simulation-optimization modeling of conjunctive use of surface water and groundwater. Water Resour. Manag. 2010, 24, 1965–1988. [Google Scholar] [CrossRef]
- Shourian, A.J.; Raoufi, M. Interbasin water transfer capacity design by two approaches of simulation-optimization and multicriteria decision making. J. Water Resour. Plan. Manag. 2017, 143, 04017054. [Google Scholar] [CrossRef]
- Zekri, S.; Triki, C.; Al-Maktoumi, A.; Bazargan-Lari, M.R. An optimization-simulation approach for groundwater abstraction under recharge uncertainty. Water Resour. Manag. 2015, 29, 3681–3695. [Google Scholar] [CrossRef]
- Smerdon, B.D.; Mendoza, C.A.; Devito, K.J. Simulations of fully coupled lake-groundwater exchange in a subhumid climate with an integrated hydrologic model. Water Resour. Res. 2007, 43, 1–13. [Google Scholar] [CrossRef]
- Zhu, Y.; Shi, L.; Lin, L.; Yang, J.; Ye, M. A fully coupled numerical modeling for regional unsaturated-saturated water flow. J. Hydrol. 2012, 475, 188–203. [Google Scholar] [CrossRef]
- Takeuchi, J.; Kawachi, T.; Imagawa, C.; Buma, N.; Unami, K.; Maeda, S. A physically based FVM watershed model fully coupling surface and subsurface water flows. Paddy Water Environ. 2010, 8, 145–156. [Google Scholar] [CrossRef]
- Harter, T.; Morel-Seytoux, H. Peer Review of the IWFM, MODFLOW and HGS Model Codes: Potential for Water Management Applications in California’s Central Valley and Other Irrigated. Excell. Consens. Water. 2013, 2013, 121. [Google Scholar]
- Ashby, S.F.; Falgout, R.D. A Parallel Multigrid Preconditioned Conjugate Gradient Algorithm for Groundwater Flow Simulations. Nucl. Sci. Eng. 1996, 124, 145–159. [Google Scholar] [CrossRef]
- Jones, J.E.; Woodward, C.S. Newton–Krylov-multigrid solvers for large-scale, highly heterogeneous, variably saturated flow problems. Adv. Water Resour. 2001, 24, 763–774. [Google Scholar] [CrossRef] [Green Version]
- Delfs, J.; Sudicky, E.A.; Park, Y.; Mclaren, R.G. An inter-comparison of two coupled hydrogeological models. In Proceedings of the XIX International Conference on Water Resources, CMWR, Urbana-Champaign, IL, USA, 17–22 June 2012; pp. 1–8. [Google Scholar]
- Kolditz, O.; Bauer, S.; Bilke, L.; Böttcher, N.; Delfs, J.O.; Fischer, T.; Görke, U.J.; Kalbacher, T.; Kosakowski, G.; McDermott, C.I.; et al. OpenGeoSys: An open-source initiative for numerical simulation of thermo-hydro-mechanical/chemical (THM/C) processes in porous media. Environ. Earth Sci. 2012, 67, 589–599. [Google Scholar] [CrossRef]
- Guay, C.; Nastev, M.; Paniconi, C.; Sulis, M. Comparison of two modeling approaches for groundwater-surface water interactions. Hydrol. Process. 2013, 27, 2258–2270. [Google Scholar] [CrossRef]
- Muma, M.; Rousseau, A.N.; Gumiere, S.J. Assessment of the impact of subsurface agricultural drainage on soilwater storage and flows of a small watershed. Water 2016, 8, 326. [Google Scholar] [CrossRef] [Green Version]
- Alcaraz, M.; Vázquez-Suñé, E.; Velasco, V.; Criollo, R. A loosely coupled GIS and hydrogeological modeling framework. Environ. Earth Sci. 2017, 76. [Google Scholar] [CrossRef]
- Bisht, G.; Huang, M.; Zhou, T.; Chen, X.; Dai, H.; Hammond, G.E.; Riley, W.J.; Downs, J.L.; Liu, Y.; Zachara, J.M. Coupling a three-dimensional subsurface flow and transport model with a land surface model to simulate stream–aquifer–land interactions (CP v1.0). Geosci. Model Dev. 2017, 10, 4539–4562. [Google Scholar] [CrossRef] [Green Version]
- Fatichi, S.; Vivoni, E.R.; Ogden, F.L.; Ivanov, V.Y.; Mirus, B.; Gochis, D.; Downer, C.W.; Camporese, M.; Davison, J.H.; Ebel, B.; et al. An overview of current applications, challenges, and future trends in distributed process-based models in hydrology. J. Hydrol. 2016, 537, 45–60. [Google Scholar] [CrossRef] [Green Version]
- Bear, V.A. Modeling Groundwater Flow and Pollution; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1987. [Google Scholar]
- Mehdinejadiani, B.; Jafari, H.; Baleanu, D. Derivation of a fractional Boussinesq equation for modelling unconfined groundwater. Eur. Phys. J. Spéc. Top. 2013, 222, 1805–1812. [Google Scholar] [CrossRef]
- Nimmo, J.R. Unsaturated Zone Flow Processes. Encycl. Hydrol. Sci. 2005, 10. [Google Scholar] [CrossRef]
- Bronstert, A.; Carrera, J.; Kabat, P.; Lütkemeier, S. (Eds.) Coupled Models for the Hydrological Cycle; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Barth, C.; Krause, P.; Boyle, D.P.; Markstrom, S.L. Hydrologic modeling of a groundwater dominated watershed using a loosely coupled modeling approach. Int. Congr. Model. Simul. Adv. Appl. Manag. Decis. Making Proc. 2005, 2015, 601–607. [Google Scholar]
- Huang, G.; Yeh, G.-T. Comparative Study of Coupling Approaches for Surface Water and Subsurface Interactions. J. Hydrol. Eng. 2009, 14, 453–462. [Google Scholar] [CrossRef]
- Barthel, R. Common problematic aspects of coupling hydrological models with groundwater flow models on the river catchment scale. Adv. Geosci. 2006, 9, 63–71. [Google Scholar] [CrossRef] [Green Version]
- Bhattarai, M.P. Impact of Climate Change on Surface and Subsurface Water Interaction and Riparian Vegetation: Linkage between Hydrology and Invasive Tamarisk in a Semi-Arid Basin; University of Nevada: Reno, NV, USA, 2013. [Google Scholar]
- Jie, Z.; van Heyden, J.; Bendel, D.; Barthel, R. Combination of soil-water balance models and water-table fluctuation methods for evaluation and improvement of groundwater recharge calculations. Hydrogeol. J. 2011, 19, 1487–1502. [Google Scholar] [CrossRef]
- Wolf, J.; Barthel, R.; Braun, J. Modeling Ground Water Flow in Alluvial Mountainous Catchments on a Watershed Scale. Ground Water 2008, 46, 695–705. [Google Scholar] [CrossRef]
- Rivard, C.; Lefebvre, R.; Paradis, D. Regional recharge estimation using multiple methods: An application in the Annapolis Valley, Nova Scotia (Canada). Environ. Earth Sci. 2013, 71, 1389–1408. [Google Scholar] [CrossRef]
- Hu, L.; Zhang, M.; Yang, Z.; Fan, Y.; Li, J.; Wang, H.; Lubale, C. Estimating dewatering in an underground mine by using a 3D finite element model. PLoS ONE 2020, 15, e0239682. [Google Scholar] [CrossRef]
- Said, A.; Stevens, D.K.; Sehlke, G. Estimating water budget in a regional aquifer using hspf-modflow integrated model. J. Am. Water Resour. Assoc. 2005, 41, 1–42. [Google Scholar] [CrossRef]
- Wilcox, L.J.; Bowman, R.S.; Shafike, N.G. Evaluation of Rio Grande management alternatives using a surface-water/ground-water model. J. Am. Water Resour. Assoc. 2007, 43, 1595–1603. [Google Scholar] [CrossRef]
- Ragab, R.; Bromley, J.; Dörflinger, G.; Katsikides, S. IHMS-Integrated hydrological modelling system. Part 2. application of linked unsaturated, DiCaSM and saturated zone, MODFLOW models on Kouris and Akrotiri catchments in Cyprus. Hydrol. Process. 2010, 24, 2681–2692. [Google Scholar] [CrossRef]
- Ragab, R.; Bromley, J. IHMS-Integrated Hydrological Modelling System. Part 1. Hydrological processes and general structure. Hydrol. Process. 2010, 24, 2663–2680. [Google Scholar] [CrossRef]
- Hassan, S.M.T.; Lubczynski, M.W.; Niswonger, R.G.; Su, Z. Surface-groundwater interactions in hard rocks in Sardon Catchment of western Spain: An integrated modeling approach. J. Hydrol. 2014, 517, 390–410. [Google Scholar] [CrossRef]
- Niswonger, R.G.; Allander, K.K.; Jeton, A.E. Collaborative modelling and integrated decision support system analysis of a developed terminal lake basin. J. Hydrol. 2014, 517, 521–537. [Google Scholar] [CrossRef]
- Tian, Y.; Zheng, Y.; Wu, B.; Wu, X.; Liu, J.; Zheng, C. Modeling surface water-groundwater interaction in arid and semi-arid regions with intensive agriculture. Environ. Model. Softw. 2015, 63, 170–184. [Google Scholar] [CrossRef]
- Surfleet, C.G.; Tullos, D. Uncertainty in hydrologic modelling for estimating hydrologic response due to climate change (Santiam River, Oregon). Hydrol. Process. 2013, 27, 3560–3576. [Google Scholar] [CrossRef] [Green Version]
- Surfleet, C.G.; Tullos, D.; Chang, H.; Jung, I.W. Selection of hydrologic modeling approaches for climate change assessment: A comparison of model scale and structures. J. Hydrol. 2012, 464–465, 233–248. [Google Scholar] [CrossRef] [Green Version]
- Højberg, A.L.; Troldborg, L.; Stisen, S.; Christensen, B.B.S.; Henriksen, H.J. Stakeholder driven update and improvement of a national water resources model. Environ. Model. Softw. 2013, 40, 202–213. [Google Scholar] [CrossRef]
- Qin, H.; Cao, G.; Kristensen, M.; Refsgaard, J.C.; Rasmussen, M.O.; He, X.; Liu, J.; Shu, Y.; Zheng, C. Integrated hydrological modeling of the North China Plain and implications for sustainable water management. Hydrol. Earth Syst. Sci. 2013, 17, 3759–3778. [Google Scholar] [CrossRef] [Green Version]
- Habets, F.; Gascoin, S.; Korkmaz, S.; Thiéry, D.; Zribi, M.; Amraoui, N.; Carli, M.; Ducharne, A.; Leblois, E.; LeDoux, E.; et al. Multi-model comparison of a major flood in the groundwater-fed basin of the Somme River (France). Hydrol. Earth Syst. Sci. 2010, 14, 99–117. [Google Scholar] [CrossRef] [Green Version]
- Miller, N.L.; Dale, L.L.; Brush, C.F.; Vicuna, S.D.; Kadir, T.N.; Dogrul, E.C.; Chung, F.I. Drought Resilience of the California Central Valley Surface-Ground-Water-Conveyance System. JAWRA J. Am. Water Resour. Assoc. 2009, 45, 857–866. [Google Scholar] [CrossRef]
- Korkmaz, S.; Ledoux, E.; Önder, H. Application of the coupled model to the Somme river basin. J. Hydrol. 2009, 366, 21–34. [Google Scholar] [CrossRef]
- LeDoux, E.; Gomez, E.; Monget, J.; Viavattene, C.; Viennot, P.; Ducharne, A.; Benoit, M.; Mignolet, C.; Schott, C.; Mary, B. Agriculture and groundwater nitrate contamination in the Seine basin. The STICS–MODCOU modelling chain. Sci. Total. Environ. 2007, 375, 33–47. [Google Scholar] [CrossRef]
- Werner, A.D.; Gallagher, M.R.; Weeks, S.W. Regional-scale, fully coupled modelling of stream-aquifer interaction in a tropical catchment. J. Hydrol. 2006, 328, 497–510. [Google Scholar] [CrossRef]
- Kim, N.W.; Chung, I.M.; Won, Y.S.; Arnold, J.G. Development and application of the integrated SWAT-MODFLOW model. J. Hydrol. 2008, 356, 1–16. [Google Scholar] [CrossRef]
- Fleckenstein, J.H.; Niswonger, R.G.; Fogg, G.E. River-aquifer interactions, geologic heterogeneity, and low-flow management. Ground Water 2006, 44, 837–852. [Google Scholar] [CrossRef] [PubMed]
- Emara, N.A.; Hussein, A.S.; Khalifa, M.E.; Abdel-Wahab, M.S. A hierarchical approach for groundwater modeling. In Proceedings of the Twelfth International Water Technology Conference, IWTC12, Alexandria, Egypt, 1 January 2008; pp. 1483–1498. [Google Scholar]
- Salama, A.; El Amin, M.F.; Kumar, K.; Sun, S. Flow and Transport in Tight and Shale Formations: A Review. Geofluids 2017, 2017, 1–21. [Google Scholar] [CrossRef] [Green Version]
- Salama, A.; Sun, S.; El Amin, M.F. An Algorithm for the Numerical Solution of the Pseudo Compressible Navier-stokes Equations Based on the Experimenting Fields Approach. Procedia Comput. Sci. 2015, 51, 1229–1238. [Google Scholar] [CrossRef] [Green Version]
- El-Amin, M.F.; Sun, S.; Salama, A. An efficient scheme for two-phase flow in porous media including dynamic capillary Pressure. In Proceedings of the World Congress on Engineering, WCE, London, UK, 2–4 July 2014; Volume 2. [Google Scholar]
- Tonkin, M.; Karanovic, M.; Hughes, A.; Jackson, C. New and Contrasting Approaches to Local Grid Refinement. In Proceedings of the MODFLOW and More 2006: Managing Ground-Water Systems, Golden, CO, USA, 16–19 September 2006; pp. 601–605. [Google Scholar]
- Afshari, S.; Mandle, R.; Li, S.-G. Hierarchical Patch Dynamics Modeling of Near-Well Dynamics in Complex Regional Groundwater Systems. J. Hydrol. Eng. 2008, 13, 894–904. [Google Scholar] [CrossRef]
- Li, S.; Liu, Q.; Afshari, S. Modeling Complex Groundwater Systems Across Multiple Scales: Part 1—A Hierarchical Patch Dynamic Paradigm; Michigan State University: East Lansing, MI, USA, 2004. [Google Scholar]
- El-Amin, M.; Salama, A.; Sun, S. Solute Transport With Chemical Reaction in Singleand Multi-Phase Flow in Porous Media. In Mass Transfer in Multiphase Systems and its Applications; IntechOpen: Cham, Switzerland, 2011. [Google Scholar]
- El-Amin, M.F.; Sun, S.; Salama, A. Modeling and Simulation of Nanoparticle Transport in Multiphase Flows in Porous Media: CO2 Sequestration. In All Days; SPE: London, UK, 2012; pp. 18–27. [Google Scholar]
- Salama, A.; Sun, S.; Wheeler, M.F. Solving global problem by considering multitude of local problems: Application to fluid flow in anisotropic porous media using the multipoint flux approximation. J. Comput. Appl. Math. 2014, 267, 117–130. [Google Scholar] [CrossRef]
- Sun, S.; Salama, A.; El Amin, M.F. Matrix-oriented implementation for the numerical solution of the partial differential equations governing flows and transport in porous media. Comput. Fluids 2012, 68, 38–46. [Google Scholar] [CrossRef]
- Zhang, T.; Salama, A.; Sun, S.; Zhong, H. A compact numerical implementation for solving Stokes equations using matrix-vector operations. Procedia Comput. Sci. 2015, 51, 1208–1218. [Google Scholar] [CrossRef] [Green Version]
- Anibas, C.; Verbeiren, B.; Buis, K.; Chormański, J.; De Doncker, L.; Okruszko, T.; Meire, P.; Batelaan, O. A hierarchical approach on groundwater-surface water interaction in wetlands along the upper Biebrza River, Poland. Hydrol. Earth Syst. Sci. 2012, 16, 2329–2346. [Google Scholar] [CrossRef] [Green Version]
- Poole, G.C.; Stanford, J.A.; Running, S.W.; Frissell, C.A.; Woessner, W.W.; Ellis, B.K. A patch hierarchy approach to modeling surface and subsurface hydrology in complex flood-plain environments. Earth Surf. Process. Landforms 2004, 29, 1259–1274. [Google Scholar] [CrossRef]
- Wang, J.L.; Jin, M.G.; Wang, Z.G.; Jia, B.J. Numerical simulation of groundwater age distributions in the hierarchical subsurface flow system: A case study of Jinan in northern China. In Proceedings of the 4th International Conference on Water Resource and Environment (WRE 2018), Kaohsiung City, Taiwan, 17–21 July 2018; Volume 191. [Google Scholar]
- Langston, G.; Hayashi, M.; Roy, J.W. Quantifying groundwater-surface water interactions in a proglacial moraine using heat and solute tracers. Water Resour. Res. 2013, 49, 5411–5426. [Google Scholar] [CrossRef]
- Saha, G.C.; Li, J.; Thring, R.W.; Hirshfield, F.; Paul, S.S. Temporal dynamics of groundwater-surface water interaction under the effects of climate change: A case study in the Kiskatinaw River Watershed, Canada. J. Hydrol. 2017, 551, 440–452. [Google Scholar] [CrossRef]
- Abiye, T.; Masindi, K.; Mengistu, H.; Demlie, M. Understanding the groundwater-level fluctuations for better management of groundwater resource: A case in the Johannesburg region. Groundw. Sustain. Dev. 2018, 7, 1–7. [Google Scholar] [CrossRef]
- Adhikary, S.K.; Gupta, A.D. A Stochastic Modelling Technique for Predicting Groundwater Table Fluctuations with Time Series Analysis. Int. J. Appl. Sci. Eng. Res. 2012, 1, 2. [Google Scholar]
- Khorasani, M.; Ehteshami, M.; Ghadimi, H.; Salari, M. Simulation and analysis of temporal changes of groundwater depth using time series modeling. Model. Earth Syst. Environ. 2016, 2, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Obergfell, C.; Bakker, M.; Maas, K. La méthode de l’onde de crue appliquée dans le cadre d’analyses de séries de niveaux piézométriques dans le but d’estimer des paramètres de modèles d’écoulement d’eau souterraine. Hydrogeol. J. 2016, 24, 1807–1819. [Google Scholar] [CrossRef]
- Bakker, M.; Schaars, F. Solving Groundwater Flow Problems with Time Series Analysis: You May Not Even Need Another Model. Ground Water 2019, 57, 826–833. [Google Scholar] [CrossRef] [Green Version]
- Shapoori, V.; Peterson, T.J.; Western, A.W.; Costelloe, J.F. Estimating aquifer properties using groundwater hydrograph modelling. Hydrol. Process. 2015, 29, 5424–5437. [Google Scholar] [CrossRef]
- Mogaji, K.A.; Lim, H.S.; Abdullah, K. Modeling of groundwater recharge using a multiple linear regression (MLR) recharge model developed from geophysical parameters: A case of groundwater resources management. Environ. Earth Sci. 2015, 73, 1217–1230. [Google Scholar] [CrossRef]
- Sahoo, S.; Jha, M.K. Prédiction du niveau de la nappe par les techniques de régression linéaire multiple et de kréseau neuronal artificiel: Évaluation comparative. Hydrogeol. J. 2013, 21, 1865–1887. [Google Scholar] [CrossRef]
- Stackelberg, P.E.; Barbash, J.E.; Gilliom, R.J.; Stone, W.W.; Wolock, D.M. Regression models for estimating concentrations of atrazine plus deethylatrazine in shallow groundwater in agricultural areas of the United States. J. Environ. Qual. 2012, 41, 479–494. [Google Scholar] [CrossRef]
- Yan, S.F.; Yu, S.E.; Wu, Y.B.; Pan, D.F.; Dong, J.G. Understanding groundwater table using a statistical model. Water Sci. Eng. 2018, 11, 1–7. [Google Scholar] [CrossRef]
- Kornelsen, K.C.; Coulibaly, P. Synthesis review on groundwater discharge to surface water in the Great Lakes Basin. J. Great Lakes Res. 2014, 40, 247–256. [Google Scholar] [CrossRef]
- Semenova, O.; Beven, K. Barriers to progress in distributed hydrological modelling. Hydrol. Process. 2015, 29, 2074–2078. [Google Scholar] [CrossRef] [Green Version]
- Paniconi, C.; Putti, M. Physically based modeling in catchment hydrology at 50: Survey and outlook. Water Resour. Res. 2015, 51, 7090–7129. [Google Scholar] [CrossRef] [Green Version]

| Available Software | Review Articles References |
|---|---|
| HydroGeosphere | [23,48] |
| ParFlow | [26,30,49,50] |
| OpenGeoSys | [51,52] |
| CATHY | [53,54] |
| InHM | [34] |
| MIKESHE-2003 version | [17] |
| HYDRUS | [17] |
| SUTRA | [16,17] |
| PAWS | [25,28] |
| PIHM | [25] |
| tRIBS + VEGGIE | [25] |
| IWFM | [55] |
| Cast3M | [28] |
| Community Land Model version 4.5 | [56] |
| GW Model and Scheme | SW System | Unsaturated System | References |
|---|---|---|---|
| FEFLOW-3D Finite element | MIKE11-1D | 2D; HELP | [69,70] |
| FHM-MODFLOW | HSPF-1D Stream Channel | Single storage reservoir-HSPF | [70] |
| MODBRANCH-MODFLOW | Saint-Venant-1D | Not Effective | [71] |
| IHMS-MODFLOW | DiCaSM | DiCaSM | [72,73] |
| GSFLOW-MODFLOW | PRMS-1D Stream Channel | 1D Kinematic Wave to Richards’ equation | [74,75,76,77,78] |
| MIKE SHE-3D Finite Difference | Saint-Venant-2D | 2-layer Water Balance Method | [79,80] |
| IWFM-Quasi 3D finite element/finite difference | Kinematic Wave Routing-1D | 1D | [81,82] |
| MODCOU-SAM | Muskingum 1D/HECRAS-1D | Soil-water Budget | [83,84] |
| MODHMS-MODFLOW | Channel Flow Package (CHF1)-1D Saint Venant | Richards’ 3D | [85] |
| SWAT-MODFLOW | SWAT | Not mentioned | [86] |
| MODFLOW-MO-FLOW | MODFLOW stream package | MODFLOW stream package | [87] |
| Advantages | Disadvantages |
|---|---|
| Refinement or subdivisions of large grid cell into smaller spatial dimensions for the area of interest yields a more precise approximation of hydraulic head or drawdown on the well scale. | The refinement process is not well suited for large-scale, regional groundwater models because of remarkable increment in computational resources [93]. |
| The solution could be obtained swiftly along with consistency between the regional and local zone around the wells, particularly for simple or small-scale. | Multiple sources and sinks, complex aquifer structure, transient flow conditions, multiple scaled of interest and strong anisotropy and heterogeneity associated with large problems would make this solution procedure very steep and might often lead to deficiency of convergence or numerical undulations [88]. |
| The regular arrangement within the child grids and the resulting reduced computational burden due to large declination in the total number of cells can be avoided [93]. | An uneven configuration across the parent-child boundary and the improvement and maintenance of separate model files are the main obstacles of this method [88]. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Haque, A.; Salama, A.; Lo, K.; Wu, P. Surface and Groundwater Interactions: A Review of Coupling Strategies in Detailed Domain Models. Hydrology 2021, 8, 35. https://doi.org/10.3390/hydrology8010035
Haque A, Salama A, Lo K, Wu P. Surface and Groundwater Interactions: A Review of Coupling Strategies in Detailed Domain Models. Hydrology. 2021; 8(1):35. https://doi.org/10.3390/hydrology8010035
Chicago/Turabian StyleHaque, Arefin, Amgad Salama, Kei Lo, and Peng Wu. 2021. "Surface and Groundwater Interactions: A Review of Coupling Strategies in Detailed Domain Models" Hydrology 8, no. 1: 35. https://doi.org/10.3390/hydrology8010035
APA StyleHaque, A., Salama, A., Lo, K., & Wu, P. (2021). Surface and Groundwater Interactions: A Review of Coupling Strategies in Detailed Domain Models. Hydrology, 8(1), 35. https://doi.org/10.3390/hydrology8010035