Analytical Models of Intra- and Extratumoral Cell Interactions at Avascular Stage of Growth in the Presence of Targeted Chemotherapy
Abstract
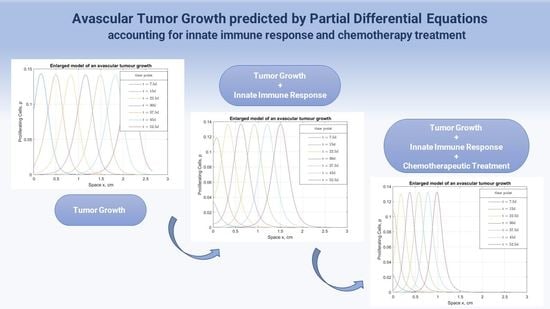
:1. Introduction
2. Mathematical Model and Methodology
2.1. Model Assumptions
- Chemotherapy and innate immune responses decrease proliferation.
- All living cells receive nutrients (consisting of glucose and oxygen) from the underlying tissue, and divide depending on the level of nutrient supply.
- Chemotherapeutic drugs attack proliferating cells, surrounding healthy cells and immune cells.
- One cell population limits the movement of the cell population of another type and vice versa—this phenomenon is called ‘contact inhibition of migration’ [6].
- The effectiveness of the nutrient source term decreases with overall cell density.
- We assume that the nutrients, the immune response, and the drug react, and diffuse over the spatial domain.
- Nutrients diffuse into the tumor space at a diffusion rate that allows for the concentration of nutrient supply to reach a steady state.
- Immune cells are generated through a steady influx into the tumor area, and proliferate within it.
2.2. Modelling Equations
3. Model Results and Validation
3.1. Chemotherapy Effect on Malignant Proliferation and Tumor Regression
3.2. The Immunity Power Effect on Tumor Evolvement under Chemotherapy
3.3. Chemotherapy’s Effect on the Surrounding Healthy Tissue and Immune System
3.4. Model Validation
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| P | Proliferating cell population density, (×109 to give units cells/cm3) |
| Q | Quiescent cell population density, (×109 to give units cells/cm3) |
| N | Necrotic cell population density, (×109 to give units cells/cm3) |
| S | Surrounding tissue cell population density, (×109 to give units cells/cm3) |
| C | Nutrient supply intake |
| L | Immune cell population density, (×109 to give units cells/cm3) |
| D | Chemotherapy drug intake |
| kDP | |
| kDQ | |
| kDS | |
| kDL | |
| DC | |
| DL | |
| DD | |
| C0 | Nutrient concentration in the absence of abnormal proliferation |
| vL | |
| k1 | |
| k2 | |
| k3 | |
| k4 | |
| k5 | |
| k6 | |
| kD | |
| α | Nutrient coefficient |
| Γ | Dimensionless parameter in Equation (4) |
| f | Functional form representing the rate of quiescent cells turning to necrotic |
| h | Functional form representing the rate of proliferating cells turning quiescent |
| g | Functional form representing the mitosis rate of proliferating cells |
| vD(t) |
References
- Araujo, R.P.; McElwain, D.S. A history of the study of solid tumour growth: The contribution of mathematical modelling. Bull. Math. Biol. 2004, 66, 1039–1091. [Google Scholar] [CrossRef]
- Melero, I.; Castanon, E.; Alvarez, M.; Champiat, S.; Marabelle, A. Intratumoural administration and tumour tissue targeting of cancer immunotherapies. Nat. Rev. Clin. Oncol. 2021, 18, 558–576. [Google Scholar] [CrossRef] [PubMed]
- Song, G.; Tian, T.; Zhang, X. A mathematical model of cell-mediated immune response to tumor. Math. Biosci. Eng. 2021, 18, 373–385. [Google Scholar] [CrossRef] [PubMed]
- Gupta, P.K.; Dhar, B. Dynamical behaviour of fractional order tumor-immune model with targeted chemotherapy treatment. Int. J. Eng. Technol. 2018, 7, 6–9. [Google Scholar] [CrossRef]
- Elkaranshawy, H.A.; Makhlouf, A.M. Parameter estimation and sensitivity analysis for a model of tumor–immune interaction in the presence of immunotherapy and chemotherapy. J. Egypt. Math. Soc. 2022, 30, 1–16. [Google Scholar] [CrossRef]
- Sherratt, J.A.; Chaplain, M.A. A new mathematical model for avascular tumour growth. J. Math. Biol. 2001, 43, 291–312. [Google Scholar] [CrossRef] [Green Version]
- Taghibakhshi, A.; Barisam, M.; Saidi, M.S.; Kashaninejad, N.; Nguyen, N.T. Three-dimensional modeling of avascular tumor growth in both static and dynamic culture platforms. Micromachines 2019, 10, 580. [Google Scholar] [CrossRef] [Green Version]
- Ansarizadeh, F.; Singh, M.; Richards, D. Modelling of Tumor Cells Regression in Response to Chemotherapeutic Treatment. Appl. Math. Model. 2017, 48, 96–112. [Google Scholar] [CrossRef]
- Pourhasanzade, F.; Sabzpoushan, S.H. A New Mathematical Model for Controlling Tumor Growth Based on Microenvironment Acidity and Oxygen Concentration. Biomed Res. Int. 2021, 2021, 8886050. [Google Scholar] [CrossRef]
- Makhlouf, A.M.; El-Shennawy, L.; Elkaranshawy, H.A. Mathematical modelling for the role of CD4+ T cells in tumor-immune interactions. Comput. Math. Methods Med. 2020, 2020, 7187602. [Google Scholar] [CrossRef] [Green Version]
- Qomlaqi, M.; Bahrami, F.; Ajami, M.; Hajati, J. An extended mathematical model of tumor growth and its interaction with the immune system, to be used for developing an optimized immunotherapy treatment protocol. Math. Biosci. 2017, 292, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Song, G.; Liang, G.; Tian, T.; Zhang, X. Mathematical Modeling and Analysis of Tumor Chemotherapy. Symmetry 2022, 14, 704. [Google Scholar] [CrossRef]
- Hussain, J.; Bano, Z.; Ahmed, W.; Shahid, S. Analysis of stochastic dynamics of tumor with drug interventions. Chaos Solit. Fractals. 2022, 157, 111932. [Google Scholar] [CrossRef]
- de Pillis, L.G.; Gu, W.; Radunskaya, A.E. Mixed immunotherapy and chemotherapy of tumors: Modeling, applications and biological interpretations. J. Theor. Biol. 2006, 238, 841–862. [Google Scholar] [CrossRef]
- Bitsouni, V.; Tsilidis, V. Mathematical modeling of tumor-immune system interactions: The effect of rituximab on breast cancer immune response. J. Theor. Biol. 2022, 539, 111001. [Google Scholar] [CrossRef]
- Mirzaei, N.M.; Su, S.; Sofia, D.; Hegarty, M.; Abdel-Rahman, M.H.; Asadpoure, A.; Cebulla, C.M.; Chang, Y.H.; Hao, W.; Jackson, P.R.; et al. Mathematical Model of Breast Tumor Progression Based on Immune Infiltration. J. Pers. Med. 2021, 11, 1031. [Google Scholar] [CrossRef]
- Ali, A.; Hussain, M.; Ghaffar, A.; Ali, Z.; Nisar, K.S.; Alharthi, M.R.; Jamshed, W. Numerical simulations and analysis for mathematical model of avascular tumor growth using Gompertz growth rate function. Alex. Eng. J. 2021, 60, 3731–3740. [Google Scholar] [CrossRef]
- Sadhukhan, S.; Basu, S.K. Avascular tumour growth models based on anomalous diffusion. J. Biol. Phys. 2020, 46, 67–94. [Google Scholar] [CrossRef]
- Michel, T.; Fehrenbach, J.; Lobjois, V.; Laurent, J.; Gomes, A.; Colin, T.; Poignard, C. Mathematical modeling of the proliferation gradient in multicellular tumor spheroids. J. Theor. Biol. 2018, 458, 133–147. [Google Scholar] [CrossRef] [Green Version]
- Malinzi, J. Mathematical analysis of a mathematical model of chemovirotherapy: Effect of drug infusion method. Comput. Math. Methods Med. 2019, 2019, 7576591. [Google Scholar] [CrossRef]
- Le, T.; Su, S.; Kirshtein, A.; Shahriyari, L. Data-Driven Mathematical Model of Osteosarcoma. Cancers 2021, 13, 2367. [Google Scholar] [CrossRef] [PubMed]
- Veeresha, P.; Prakasha, D.G.; Baskonus, H.M. New numerical surfaces to the mathematical model of cancer chemotherapy effect in Caputo fractional derivatives. Chaos 2019, 29, 013119. [Google Scholar] [CrossRef] [PubMed]
- De Pillis, L.G.; Radunskaya, A. The dynamics of an optimally controlled tumor model: A case study. Math. Comput. Model. 2003, 37, 1221–1244. [Google Scholar] [CrossRef]
- Swanson, K.R.; Rockne, R.C.; Claridge, J.; Chaplain, M.A.; Alvord Jr, E.C.; Anderson, A.R. Quantifying the role of angiogenesis in malignant progression of gliomas: In silico modeling integrates imaging and histology. Cancer Res. 2011, 71, 7366–7375. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hinow, P.; Gerlee, P.; McCawley, L.J.; Quaranta, V.; Ciobanu, M.; Wang, S.; Graham, J.M.; Ayati, B.P.; Claridge, J.; Swanson, K.R.; et al. A spatial model of tumor-host interaction: Application of chemotherapy. Math. Biosci. Eng. 2009, 6, 521. [Google Scholar]
- Chicoine, M.R.; Silbergeld, D.L. Assessment of brain tumor cell motility in vivo and in vitro. J. Neurosurg. 1995, 82, 615–622. [Google Scholar] [CrossRef]
- Wang, Z.; Kerketta, R.; Chuang, Y.L.; Dogra, P.; Butner, J.D.; Brocato, T.A.; Day, A.; Xu, R.; Shen, H.; Simbawa, E.; et al. Theory and experimental validation of a spatio-temporal model of chemotherapy transport to enhance tumor cell kill. PLoS Comput. Biol. 2016, 12, 1004969. [Google Scholar] [CrossRef] [Green Version]
- Ku-Carrillo, R.A.; Delgadillo, S.E.; Chen-Charpentier, B.M. A mathematical model for the effect of obesity on cancer growth and on the immune system response. Appl. Math. Model. 2016, 40, 4908–4920. [Google Scholar] [CrossRef]





| Parameter | Generalized Tumor Cells | Cell Populations of a Tumor | Surrounding Healthy Tissue Cells | Innate Immune Cells (Varied) | Chemotherapeutic Drug Effect | Nutrients | Immunotherapy Effect | Other | ||
|---|---|---|---|---|---|---|---|---|---|---|
| Author | Proliferating Cells | Quiescent Cells | Necrotic Cells | |||||||
| This study | ⁕ | ⁕ | ⁕ | ⁕ | ⁕ | ⁕ | ⁕ | |||
| [4] | ⁕ | ⁕ | ⁕ | |||||||
| [19] | ⁕ | ⁕ | ⁕ | |||||||
| [17] | ⁕ | ⁕ | ⁕ | ⁕ | ⁕ | |||||
| [7] | ⁕ | ⁕ | ⁕ | ⁕ | ||||||
| [9] | ⁕ | ⁕ | ⁕ | ⁕ | ⁕ | |||||
| [12] | ⁕ | ⁕ | ⁕ | |||||||
| [3] | ⁕ | ⁕ | ||||||||
| [18] | ⁕ | ⁕ | ⁕ | ⁕ | ⁕ | |||||
| [16] | ⁕ | ⁕ | ⁕ | |||||||
| [5] | ⁕ | ⁕ | ⁕ | ⁕ | ||||||
| [20] | ⁕ | ⁕ | ⁕ | |||||||
| [14] | ⁕ | ⁕ | ⁕ | ⁕ | ||||||
| [6] | ⁕ | ⁕ | ⁕ | ⁕ | ⁕ | |||||
| [10] | ⁕ | ⁕ | ⁕ | ⁕ | ||||||
| [11] | ⁕ | ⁕ | ⁕ | |||||||
| [13] | ⁕ | ⁕ | ⁕ | ⁕ | ||||||
| [15] | ⁕ | ⁕ | ⁕ | |||||||
| [21] | ⁕ | ⁕ | ⁕ | |||||||
| [8] | ⁕ | ⁕ | ⁕ | ⁕ | ||||||
| Parameter | Value | Unit | Reference | Description |
|---|---|---|---|---|
| 0.3 | [8] | Fraction cell kill rate of proliferating cells under chemotherapeutic drug effect (value used for generalized tumor cells) | ||
| 0.1 | [8] | Fraction cell kill rate of quiescent cells under chemotherapeutic drug effect (assumed the same as for healthy cells) | ||
| 0.1 | [8] | Fraction cell kill rate of healthy surrounding tissue cells under chemotherapeutic drug effect | ||
| 0.2 | [8] | Fraction cell kill rate of immune system cells under chemotherapeutic drug effect | ||
| 10 | [6] | Diffusion coefficient of the nutrient | ||
| 5 | estimated | Diffusion coefficient of the immune system cells | ||
| 8 | estimated | Diffusion coefficient of a chemotherapeutic drug | ||
| 1 | dimensionless | [6] | Nutrient concentration in the absence of abnormal proliferation | |
| 0.2 | [22] | Rate of the external immune cell influx | ||
| 8 | [6] | Decay rate of the nutrient | ||
| 1 | [6] | Rate of the nutrient consumption by proliferating cells | ||
| 1 | [6] | Rate of the nutrient consumption by quiescent cells | ||
| 1 | [8] | Rate of immune cells death after contacting proliferating cells | ||
| 0.55 | [8] | Rate of proliferating cells death after contacting immune cells | ||
| 1 | estimated | Rate of the nutrient consumption by immune cells | ||
| 0.2 | [23] | Decay rate of a chemotherapeutic drug | ||
| α | 0.8 | dimensionless | [6] | Nutrient coefficient |
| Γ | 0.4 | dimensionless | [6] | Dimensionless parameter |
| Parameter | Present Model | Lit. Model [24] | Lit. Model [25] | Experiment [26] |
|---|---|---|---|---|
| Density of proliferating cells (before chemotherapy) | 0.145 × 109 cells/cm3 | 0.20 × 109 cells/cm3 (normoxic tumor cells) | 0.15 × 109 cells/cm3 (normalized density of cancer cells) | |
| Density of necrotic cells | 0.75 × 109 cells/cm3 | 0.95 × 109 cells/cm3 (necrotic tissue) | ||
| Density of proliferating cells (after chemotherapy) | 0.13 × 109 cells/cm3 | 0.1 × 109 cells/cm3 (normoxic tumor cells) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lavrenteva, E.; Theodoropoulos, C.; Binns, M. Analytical Models of Intra- and Extratumoral Cell Interactions at Avascular Stage of Growth in the Presence of Targeted Chemotherapy. Bioengineering 2023, 10, 385. https://doi.org/10.3390/bioengineering10030385
Lavrenteva E, Theodoropoulos C, Binns M. Analytical Models of Intra- and Extratumoral Cell Interactions at Avascular Stage of Growth in the Presence of Targeted Chemotherapy. Bioengineering. 2023; 10(3):385. https://doi.org/10.3390/bioengineering10030385
Chicago/Turabian StyleLavrenteva, Evgeniia, Constantinos Theodoropoulos, and Michael Binns. 2023. "Analytical Models of Intra- and Extratumoral Cell Interactions at Avascular Stage of Growth in the Presence of Targeted Chemotherapy" Bioengineering 10, no. 3: 385. https://doi.org/10.3390/bioengineering10030385
APA StyleLavrenteva, E., Theodoropoulos, C., & Binns, M. (2023). Analytical Models of Intra- and Extratumoral Cell Interactions at Avascular Stage of Growth in the Presence of Targeted Chemotherapy. Bioengineering, 10(3), 385. https://doi.org/10.3390/bioengineering10030385