Regulated Self-Folding in Multi-Layered Hydrogels Considered with an Interfacial Layer
Abstract
:1. Introduction
2. Results and Discussion
2.1. Mechanical Properties of Individual Layers in Multi-Layered Hydrogels
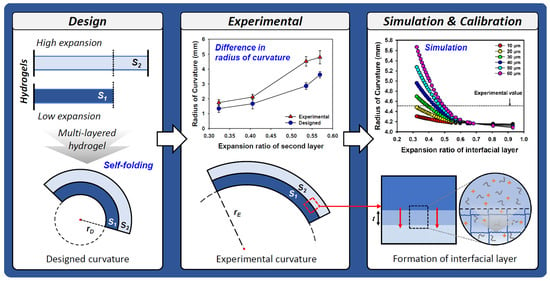
2.2. Design and Fabrication of Multi-Layered Hydrogels
2.3. Curvature Simulation of Multi-Layered Hydrogels
2.4. Evaluation of the Interfacial Layer in Multi-Layered Hydrogels
3. Conclusions
4. Materials and Methods
4.1. Hydrogel Preparation
4.2. Characterizations of Hydrogels
4.3. Design and Fabrication of the Multi-Layered Hydrogels
4.4. Characterization and Simulation of Multi-Layered Hydrogels
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cho, S.; Shin, S.G.; Kim, H.; Han, S.R.; Jeong, J.H. Self-folding of Multi-layered Hydrogel Designed for Biological Machine. Polymer 2017, 41, 346–351. [Google Scholar] [CrossRef]
- Lim, J.W.; Kim, H.J.; Kim, Y.; Shin, S.G.; Cho, S.; Jung, W.G.; Jeong, J.H. An active and soft hydrogel actuator to stimulate live cell clusters by self-folding. Polymers 2020, 12, 583. [Google Scholar] [CrossRef] [PubMed]
- Duan, J.; Liang, X.; Zhu, K.; Guo, J.; Zhang, L. Bilayer hydrogel actuators with tight interfacial adhesion fully constructed from natural polysaccharides. Soft Matter 2017, 13, 345–354. [Google Scholar] [CrossRef] [PubMed]
- Bassik, N.; Abebe, B.; Laflin, K.; Gracias, D. Photolithographically patterned smart hydrogel based bilayer actuators. Polymer 2010, 51, 6093–6098. [Google Scholar] [CrossRef]
- Baek, K.; Jeong, J.H.; Shkμmatov, A.; Bashir, R.; Kong, H. In Situ Self-Folding Assembly of a Multi-Walled Hydrogel Tube for Uniaxial Sustained Molecular Release. Adv. Mater. 2013, 25, 5568–5573. [Google Scholar] [CrossRef] [PubMed]
- Chelu, M.; Musuc, A.M. Polymer Gels: Classification and Recent Developments in Biomedical Applications. Gels 2023, 9, 161. [Google Scholar] [CrossRef] [PubMed]
- Guo, J.L.; Longaker, M. Bioprinted Hydrogels for Fibrosis and Wound Healing: Treatment and Modeling. Gels 2023, 9, 19. [Google Scholar] [CrossRef] [PubMed]
- Antich, C.; JimUnez, G.; de Vicente, J.; Lopez-Ruiz, E.; Chocarro-Wrona, C.; Grinan-Lison, C.; Carrillo, E.; Montanez, E.; Marchal, J.A. Development of a Biomimetic Hydrogel Based on Predifferentiated Mesenchymal Stem-Cell-Derived ECM for Cartilage Tissue Engineering. Adv. Healthc. Mater. 2021, 10, 2001847. [Google Scholar] [CrossRef]
- Mitragotri, S.; Lahann, J. Physical approaches to biomaterial design. Nat. Mater. 2009, 8, 15–23. [Google Scholar] [CrossRef]
- Martínez-Sanz, M.; Mikkelsen, D.; Flanagan, B.; Gidley, M.J.; Gilbert, E.P. Multi-scale model for the hierarchical architecture of native cellulose hydrogels. Carbohydr. Polym. 2016, 147, 542–555. [Google Scholar] [CrossRef]
- Xu, R.; Hua, M.; Wu, S.; Ma, S.; Zhang, Y.; Zhang, L.; Yu, B.; Cai, M.; He, X.; Zhou, F. Continuously growing multi-layered hydrogel structures with seamless interlocked interface. Matter 2022, 5, 634–653. [Google Scholar] [CrossRef]
- Schmidt, B.V. Multicompartment hydrogels. Macromol. Rapid Commun. 2022, 43, 2100895. [Google Scholar] [CrossRef] [PubMed]
- Lou, D.; Sun, Y.; Li, J.; Zheng, Y.; Zhou, Z.; Yang, J.; Pan, C.; Zheng, Z.; Chen, X.; Liu, W. Double lock label based on thermosensitive polymer hydrogels for information camouflage and multilevel encryption. Angew. Chem. 2022, 134, e202117066. [Google Scholar] [CrossRef]
- Ma, C.; Lu, W.; Yang, X.; He, J.; Le, X.; Wang, L.; Zhang, J.; Serpe, M.J.; Huang, Y.; Chen, T. Bioinspired anisotropic hydrogel actuators with on–off switchable and color-tunable fluorescence behaviors. Adv. Funct. Mater. 2018, 28, 1704568. [Google Scholar] [CrossRef]
- Jeong, J.H.; Schmidt, J.J.; Cha, C.; Kong, H. Tuning responsiveness and structural integrity of a pH responsive hydrogel using a poly (ethylene glycol) cross-linker. Soft Matter 2010, 6, 3930–3938. [Google Scholar] [CrossRef]
- Xu, B.; Jiang, H.; Li, H.; Zhang, G.; Zhang, Q. High strength nanocomposite hydrogel bilayer with bidirectional bending and shape switching behaviors for soft actuators. RSC Adv. 2015, 5, 13167–13170. [Google Scholar] [CrossRef]
- Lei, J.; Zhou, Z.; Liu, Z. Side Chains and the Insufficient Lubrication of Water in Polyacrylamide Hydrogel—A New Insight. Polymers 2019, 11, 1845. [Google Scholar] [CrossRef] [PubMed]
- Tan, J.; Xie, S.; Wang, G.; Yu, C.W.; Zeng, T.; Cai, P.; Huang, H. Fabrication and Optimization of the Thermo-Sensitive Hydrogel Carboxymethyl Cellulose/Poly (N-isopropylacrylamide-co-acrylic acid) for U (VI) Removal from Aqueous Solution. Polymers 2020, 12, 151. [Google Scholar] [CrossRef]
- He, X.; Sun, Y.; Wu, J.; Wang, Y.; Chen, F.; Fan, P.; Zhong, M.; Xiao, S.; Zhang, D.; Yang, J.; et al. Dual-stimulus bilayer hydrogel actuators with rapid, reversible, bidirectional bending behaviors. J. Mater. Chem. C 2019, 7, 4897–5210. [Google Scholar] [CrossRef]
- Sackett, S.D.; Tremmel, D.M.; Ma, F.; Feeney, A.K.; Maguire, R.M.; Brown, M.E.; Zhou, Y.; Li, X.; O’Brien, C.; Li, L.; et al. Extracellular matrix scaffold and hydrogel derived from decellularized and delipidized human pancreas. Sci. Rep. 2018, 8, 10452. [Google Scholar] [CrossRef]
- Ionov, L. Biomimetic Hydrogel-Based Actuating Systems. Adv. Funct. Mater. 2013, 23, 4555–4570. [Google Scholar] [CrossRef]
- Hamley, I.; Castelletto, V. Biological soft materials. Angew. Chem. Int. Ed. 2007, 46, 4442–4455. [Google Scholar] [CrossRef] [PubMed]
- Loi, G.; Stucchi, G.; Scocozza, F.; Cansolino, L.; Cadamuro, F.; Delgrosso, E.; Riva, F.; Ferrari, C.; Russo, L.; Conti, M. Characterization of a Bioink Combining Extracellular Matrix-like Hydrogel with Osteosarcoma Cells: Preliminary Results. Gels 2023, 9, 129. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Huang, H.; Liu, H.; Rehfeldt, F.; Wang, X.; Zhang, K. Multi-Responsive Bilayer Hydrogel Actuators with Programmable and Precisely Tunable Motions. Macromol. Chem. Phys. 2019, 220, 1800562. [Google Scholar] [CrossRef]
- Vasudevan, M.; Johnson, W. Thermal Bending of a Tri-Metal Strip. Aeronaut. J. 1961, 44, 507–509. [Google Scholar] [CrossRef]






| Sample | First Layer | Second Layer | ||||||
|---|---|---|---|---|---|---|---|---|
| Aam a | MBA b | Irgacure 2595 c | Expansion Ratio d | Aam a | MBA b | Irgacure 2595 c | Expansion Ratio d | |
| BH-1 | 20 | 0.04 | 0.2 | 0.681 | 20 | 0.30 | 0.2 | 0.569 |
| BH-2 | 20 | 0.04 | 0.2 | 0.681 | 20 | 0.20 | 0.2 | 0.536 |
| BH-3 | 20 | 0.04 | 0.2 | 0.681 | 20 | 0.10 | 0.2 | 0.406 |
| BH-4 | 20 | 0.04 | 0.2 | 0.681 | 20 | 0.08 | 0.2 | 0.385 |
| BH-5 | 20 | 0.04 | 0.2 | 0.406 | 20 | 0.04 | 0.2 | 0.681 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lim, J.W.; Kim, S.J.; Jeong, J.; Shin, S.G.; Woo, C.; Jung, W.; Jeong, J.H. Regulated Self-Folding in Multi-Layered Hydrogels Considered with an Interfacial Layer. Gels 2024, 10, 48. https://doi.org/10.3390/gels10010048
Lim JW, Kim SJ, Jeong J, Shin SG, Woo C, Jung W, Jeong JH. Regulated Self-Folding in Multi-Layered Hydrogels Considered with an Interfacial Layer. Gels. 2024; 10(1):48. https://doi.org/10.3390/gels10010048
Chicago/Turabian StyleLim, Jun Woo, Sang Jin Kim, Jimin Jeong, Sung Gyu Shin, Chaewon Woo, Woonggyu Jung, and Jae Hyun Jeong. 2024. "Regulated Self-Folding in Multi-Layered Hydrogels Considered with an Interfacial Layer" Gels 10, no. 1: 48. https://doi.org/10.3390/gels10010048
APA StyleLim, J. W., Kim, S. J., Jeong, J., Shin, S. G., Woo, C., Jung, W., & Jeong, J. H. (2024). Regulated Self-Folding in Multi-Layered Hydrogels Considered with an Interfacial Layer. Gels, 10(1), 48. https://doi.org/10.3390/gels10010048