Accounting for Cooperativity in the Thermotropic Volume Phase Transition of Smart Microgels
Abstract
:1. Introduction
2. Theory
Hill-Like Equation
3. Results and Discussion
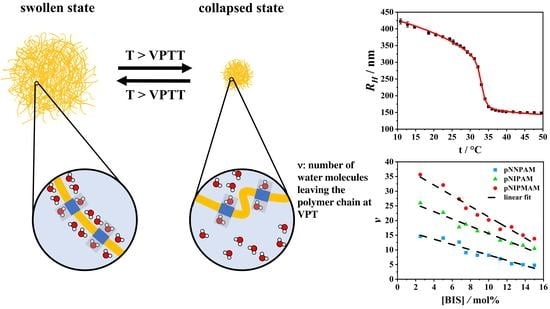
3.1. Average Degree of Polymerization
3.2. Half-Saturation Constant K
3.3. Hill Parameter
4. Conclusions
5. Materials and Methods
5.1. Chemicals
5.2. Synthesis of the Homopolymer Microgels
5.3. Photon Correlation Spectroscopy (PCS)
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pelton, R. Temperature-sensitive aqueous microgels. Adv. Colloid Interface Sci. 2000, 85, 1–33. [Google Scholar] [CrossRef]
- Thorne, J.B.; Vine, G.J.; Snowden, M.J. Microgel applications and commercial considerations. Colloid Polym. Sci. 2011, 289, 625–646. [Google Scholar] [CrossRef]
- Saunders, B.R.; Vincent, B. Microgel particles as model colloids: Theory, properties and applications. Adv. Colloid Interface Sci. 1999, 80, 1–25. [Google Scholar] [CrossRef]
- Wedel, B.; Zeiser, M.; Hellweg, T. Non NIPAM Based Smart Microgels: Systematic Variation of the Volume Phase Transition Temperature by Copolymerization. Z. FÜR Phys. Chem. 2012, 226, 737–748. [Google Scholar] [CrossRef]
- Karg, M.; Pich, A.; Hellweg, T.; Hoare, T.; Lyon, L.A.; Crassous, J.J.; Suzuki, D.; Gumerov, R.A.; Schneider, S.; Potemkin, I.I.; et al. Nanogels and Microgels: From Model Colloids to Applications, Recent Developments, and Future Trends. Langmuir Acs J. Surfaces Colloids 2019, 35, 6231–6255. [Google Scholar] [CrossRef]
- Nayak, S.; Lyon, L.A. Weiche Nanotechnologie mit weichen Nanopartikeln. Angew. Chem. 2005, 117, 7862–7886. [Google Scholar] [CrossRef]
- Plamper, F.A.; Richtering, W. Functional Microgels and Microgel Systems. Accounts Chem. Res. 2017, 50, 131–140. [Google Scholar] [CrossRef] [PubMed]
- Richtering, W.; Saunders, B.R. Gel architectures and their complexity. Soft Matter 2014, 10, 3695–3702. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pich, A.; Albrecht, K. (Eds.) Chemical Design of Responsive Microgels, 2010th ed.; Advances in Polymer Science; Springer: Berlin/Heidelberg, Germany, 2011; Volume 234. [Google Scholar] [CrossRef]
- Park, T.G.; Hoffman, A.S. Immobilization and characterization of beta-galactosidase in thermally reversible hydrogel beads. J. Biomed. Mater. Res. 1990, 24, 21–38. [Google Scholar] [CrossRef] [PubMed]
- Welsch, N.; Becker, A.L.; Dzubiella, J.; Ballauff, M. Core–shell microgels as “smart” carriers for enzymes. Soft Matter 2012, 8, 1428–1436. [Google Scholar] [CrossRef]
- Langer, R. New methods of drug delivery. Science 1990, 249, 1527–1533. [Google Scholar] [CrossRef]
- Smeets, N.M.B.; Hoare, T. Designing responsive microgels for drug delivery applications. J. Polym. Sci. Part Polym. Chem. 2013, 51, 3027–3043. [Google Scholar] [CrossRef]
- Uhlig, K.; Wegener, T.; He, J.; Zeiser, M.; Bookhold, J.; Dewald, I.; Godino, N.; Jaeger, M.; Hellweg, T.; Fery, A.; et al. Patterned Thermoresponsive Microgel Coatings for Noninvasive Processing of Adherent Cells. Biomacromolecules 2016, 17, 1110–1116. [Google Scholar] [CrossRef]
- Lu, Y.; Mei, Y.; Drechsler, M.; Ballauff, M. Thermosensitive core-shell particles as carriers for ag nanoparticles: Modulating the catalytic activity by a phase transition in networks. Angew. Chem. 2006, 45, 813–816. [Google Scholar] [CrossRef]
- Sabadasch, V.; Wiehemeier, L.; Kottke, T.; Hellweg, T. Core–shell microgels as thermoresponsive carriers for catalytic palladium nanoparticles. Soft Matter 2020, 16, 5422–5430. [Google Scholar] [CrossRef]
- Lu, Y.; Spyra, P.; Mei, Y.; Ballauff, M.; Pich, A. Composite Hydrogels: Robust Carriers for Catalytic Nanoparticles. Macromol. Chem. Phys. 2007, 208, 254–261. [Google Scholar] [CrossRef]
- Quesada-Pérez, M.; Maroto-Centeno, J.A.; Forcada, J.; Hidalgo-Alvarez, R. Gel swelling theories: The classical formalism and recent approaches. Soft Matter 2011, 7, 10536. [Google Scholar] [CrossRef]
- Hertle, Y.; Zeiser, M.; Hasenöhrl, C.; Busch, P.; Hellweg, T. Responsive P(NIPAM-co-NtBAM) microgels: Flory–Rehner description of the swelling behaviour. Colloid Polym. Sci. 2010, 288, 1047–1059. [Google Scholar] [CrossRef]
- Wu, C.; Zhou, S. Volume Phase Transition of Swollen Gels: Discontinuous or Continuous? Macromolecules 1997, 30, 574–576. [Google Scholar] [CrossRef]
- Duracher, D.; Elassari, A.; Pichot, C. Preparation of poly(N-isopropylmethacrylamide) latexes kinetic studies and characterization. J. Polym. Sci. Part Polym. Chem. 1999, 37, 1823–1837. [Google Scholar] [CrossRef]
- Shibayama, M.; Tanaka, T. Small–angle neutron scattering study on weakly charged poly(N–isopropyl acrylamide–co–acrylic acid) copolymer solutions. J. Chem. Phys. 1998, 102, 9392. [Google Scholar] [CrossRef]
- Tanaka, T.; Fillmore, D.J. Kinetics of swelling of gels. J. Chem. Phys. 1979, 70, 1214–1218. [Google Scholar] [CrossRef]
- Gehrke, S.H. Synthesis, equilibrium swelling, kinetics, permeability and applications of environmentally responsive gels. In Responsive Gels: Volume Transitions II; Dušek, K., Ed.; Advances in Polymer Science; Springer: Berlin/Heidelberg, Germany, 1993; Volume 110, pp. 81–144. [Google Scholar] [CrossRef]
- Pelton, R.H.; Chibante, P. Preparation of aqueous latices with N-isopropylacrylamide. Colloids Surfaces 1986, 20, 247–256. [Google Scholar] [CrossRef]
- Pich, A.; Lu, Y.; Boyko, V.; Arndt, K.F.; Adler, H.J.P. Thermo-sensitive poly(N-vinylcaprolactam-co-acetoacetoxyethyl methacrylate) microgels: 2. Incorporation of polypyrrole. Polymer 2003, 44, 7651–7659. [Google Scholar] [CrossRef]
- Wrede, O.; Reimann, Y.; Lülsdorf, S.; Emmrich, D.; Schneider, K.; Schmid, A.J.; Zauser, D.; Hannappel, Y.; Beyer, A.; Schweins, R.; et al. Volume phase transition kinetics of smart N-n-propylacrylamide microgels studied by time-resolved pressure jump small angle neutron scattering. Sci. Rep. 2018, 8, 13781. [Google Scholar] [CrossRef] [PubMed]
- Berndt, I.; Richtering, W. Doubly Temperature Sensitive Core-Shell Microgels. Macromolecules 2003, 36, 8780–8785. [Google Scholar] [CrossRef]
- Flory, P.J.; Rehner, J. Statistical Mechanics of Cross–Linked Polymer Networks I. Rubberlike Elasticity. J. Chem. Phys. 1943, 11, 512–520. [Google Scholar] [CrossRef]
- Flory, P.J. Principles of Polymer Chemistry, 19th ed.; Cornell Univ. Press: Ithaca, NY, USA, 1953. [Google Scholar]
- Dušek, K.; Patterson, D. Transition in swollen polymer networks induced by intramolecular condensation. J. Polym. Sci. Part Polym. Phys. 1968, 6, 1209–1216. [Google Scholar] [CrossRef]
- Flory, P.J. Fifteenth Spiers Memorial Lecture. Thermodynamics of polymer solutions. Discuss. Faraday Soc. 1970, 49, 7. [Google Scholar] [CrossRef]
- Graessley, W.W. Polymeric Liquids and Networks: Structure and Properties; Garland Science: New York, NY, USA, 2004. [Google Scholar]
- Dušek, K. (Ed.) Responsive Gels: Volume Transitions II; Advances in Polymer Science; Springer: Berlin/Heidelberg, Germany, 1993; Volume 110. [Google Scholar] [CrossRef]
- Fernández-Barbero, A.; Fernández-Nieves, A.; Grillo, I.; López-Cabarcos, E. Structural modifications in the swelling of inhomogeneous microgels by light and neutron scattering. Phys. Rev. Stat. Nonlinear Soft Matter Phys. 2002, 66, 051803. [Google Scholar] [CrossRef]
- Fernandes, P.A.L.; Schmidt, S.; Zeiser, M.; Fery, A.; Hellweg, T. Swelling and mechanical properties of polymer gels with cross-linking gradient. Soft Matter 2010, 6, 3455. [Google Scholar] [CrossRef]
- Bergmann, S.; Wrede, O.; Huser, T.; Hellweg, T. Super-resolution optical microscopy resolves network morphology of smart colloidal microgels. Phys. Chem. Chem. Phys. PCCP 2018, 20, 5074–5083. [Google Scholar] [CrossRef] [PubMed]
- Wrede, O.; Bergmann, S.; Hannappel, Y.; Hellweg, T.; Huser, T. Smart microgels investigated by super-resolution fluorescence microscopy: Influence of the monomer structure on the particle morphology. Soft Matter 2020, 16, 8078–8084. [Google Scholar] [CrossRef] [PubMed]
- Stieger, M.; Richtering, W.; Pedersen, J.S.; Lindner, P. Small-angle neutron scattering study of structural changes in temperature sensitive microgel colloids. J. Chem. Phys. 2004, 120, 6197–6206. [Google Scholar] [CrossRef]
- Arleth, L.; Xia, X.; Hjelm, R.P.; Wu, J.; Hu, Z. Volume transition and internal structures of small poly(N-isopropylacrylamide) microgels. J. Polym. Sci. Part Polym. Phys. 2005, 43, 849–860. [Google Scholar] [CrossRef]
- Neuburger, N.A.; Eichinger, B.E. Critical experimental test of the Flory-Rehner theory of swelling. Macromolecules 1988, 21, 3060–3070. [Google Scholar] [CrossRef]
- Lopez, C.G.; Richtering, W. Does Flory-Rehner theory quantitatively describe the swelling of thermoresponsive microgels? Soft Matter 2017, 13, 8271–8280. [Google Scholar] [CrossRef]
- Erman, B.; Flory, P.J. Critical phenomena and transitions in swollen polymer networks and in linear macromolecules. Macromolecules 1986, 19, 2342–2353. [Google Scholar] [CrossRef]
- Lietor-Santos, J.J.; Sierra-Martin, B.; Vavrin, R.; Hu, Z.; Gasser, U.; Fernandez-Nieves, A. Deswelling Microgel Particles Using Hydrostatic Pressure. Macromolecules 2009, 42, 6225–6230. [Google Scholar] [CrossRef] [Green Version]
- Voudouris, P.; Florea, D.; van der Schoot, P.; Wyss, H.M. Micromechanics of temperature sensitive microgels: Dip in the Poisson ratio near the LCST. Soft Matter 2013, 9, 7158. [Google Scholar] [CrossRef] [Green Version]
- Nigro, V.; Angelini, R.; Bertoldo, M.; Bruni, F.; Ricci, M.A.; Ruzicka, B. Dynamical behavior of microgels of interpenetrated polymer networks. Soft Matter 2017, 13, 5185–5193. [Google Scholar] [CrossRef]
- Nigro, V.; Angelini, R.; Rosi, B.; Bertoldo, M.; Buratti, E.; Casciardi, S.; Sennato, S.; Ruzicka, B. Study of network composition in interpenetrating polymer networks of poly(N isopropylacrylamide) microgels: The role of poly(acrylic acid). J. Colloid Interface Sci. 2019, 545, 210–219. [Google Scholar] [CrossRef] [Green Version]
- Leite, D.C.; Kakorin, S.; Hertle, Y.; Hellweg, T.; da Silveira, N.P. Smart Starch-Poly( N-isopropylacrylamide) Hybrid Microgels: Synthesis, Structure, and Swelling Behavior. Langmuir ACS J. Surfaces Colloids 2018, 34, 10943–10954. [Google Scholar] [CrossRef]
- Hino, T.; Prausnitz, J.M. Swelling equilibria for heterogeneous polyacrylamide gels. J. Appl. Polym. Sci. 1996, 62, 1635–1640. [Google Scholar] [CrossRef]
- Hill, A.V. The possible effects of the aggregation of the molecules of haemoglobin on its dissociation curves. J. Physiol. 1910, 40, 4–7. [Google Scholar]
- Cors, M.; Wiehemeier, L.; Hertle, Y.; Feoktystov, A.; Cousin, F.; Hellweg, T.; Oberdisse, J. Determination of Internal Density Profiles of Smart Acrylamide-Based Microgels by Small-Angle Neutron Scattering: A Multishell Reverse Monte Carlo Approach. Langmuir 2018, 34, 15403–15415. [Google Scholar] [CrossRef]
- López-León, T.; Fernández-Nieves, A. Macroscopically probing the entropic influence of ions: Deswelling neutral microgels with salt. Phys. Rev. Stat. Nonlinear Soft Matter Phys. 2007, 75, 011801. [Google Scholar] [CrossRef] [PubMed]
- Sierra-Martín, B.; Romero-Cano, M.S.; Fernández-Nieves, A.; Fernández-Barbero, A. Thermal control over the electrophoresis of soft colloidal particles. Langmuir ACS J. Surfaces Colloids 2006, 22, 3586–3590. [Google Scholar] [CrossRef] [PubMed]
- Witte, J.; Kyrey, T.; Lutzki, J.; Dahl, A.M.; Houston, J.; Radulescu, A.; Pipich, V.; Stingaciu, L.; Kühnhammer, M.; Witt, M.U.; et al. A comparison of the network structure and inner dynamics of homogeneously and heterogeneously crosslinked PNIPAM microgels with high crosslinker content. Soft Matter 2019, 15, 1053–1064. [Google Scholar] [CrossRef] [Green Version]
- Matsuo, E.S.; Tanaka, T. Kinetics of discontinuous volume–phase transition of gels. J. Chem. Phys. 1988, 89, 1695–1703. [Google Scholar] [CrossRef]
- Shibayama, M.; Tanaka, T.; Han, C.C. Small angle neutron scattering study on poly(N-isopropyl acrylamide) gels near their volume-phase transition temperature. J. Chem. Phys. 1992, 97, 6829–6841. [Google Scholar] [CrossRef]
- Hirotsu, S. Coexistence of phases and the nature of the 1st-order phase-transition in poly(N-isopropylacrylamide) gels. Adv. Polym. Sci. 1993, 110, 1–26. [Google Scholar]
- Chiessi, E.; Paradossi, G. Influence of Tacticity on Hydrophobicity of Poly(N-isopropylacrylamide): A Single Chain Molecular Dynamics Simulation Study. J. Phys. Chem. B 2016, 120, 3765–3776. [Google Scholar] [CrossRef] [PubMed]
- Tavagnacco, L.; Zaccarelli, E.; Chiessi, E. On the molecular origin of the cooperative coil-to-globule transition of poly(N-isopropylacrylamide) in water. Phys. Chem. Chem. Phys. PCCP 2018, 20, 9997–10010. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- de Oliveira, T.E.; Marques, C.M.; Netz, P.A. Molecular dynamics study of the LCST transition in aqueous poly(N-n-propylacrylamide). Phys. Chem. Chem. Phys. PCCP 2018, 20, 10100–10107. [Google Scholar] [CrossRef]
- Hirano, T.; Nakamura, K.; Kamikubo, T.; Ishii, S.; Tani, K.; Mori, T.; Sato, T. Hydrogen-bond-assisted syndiotactic-specific radical polymerizations ofN-alkylacrylamides: The effect of theN-substituents on the stereospecificities and unusual large hysteresis in the phase-transition behavior of aqueous solution of syndiotactic poly(N-n-propylacrylamide). J. Polym. Sci. Part Polym. Chem. 2008, 46, 4575–4583. [Google Scholar] [CrossRef]
- Provencher, S.W. CONTIN: A general purpose constrained regularization program for inverting noisy linear algebraic and integral equations. Comput. Phys. Commun. 1982, 27, 229–242. [Google Scholar] [CrossRef]





| [BIS]/mol% | ||||||
|---|---|---|---|---|---|---|
| p(NNPAM) | 5.00 | 0.057 | 14.0 | 153.5 | 23.2 | 23.2 |
| 10.0 | 20.00 | 8.16 | 43.28 | 24.1 | 23.9 | |
| 15.0 | 260.0 | 4.77 | 19.43 | 24.4 | 24.0 | |
| p(NIPAM) | 5.00 | 0.307 | 22.7 | 213.8 | 35.4 | 35.7 |
| 10.0 | 20.00 | 15.6 | 57.40 | 36.8 | 37.1 | |
| 15.0 | 230.0 | 10.5 | 27.50 | 37.8 | 38.6 | |
| p(NIPMAM) | 5.00 | 8.000 | 32.1 | 209.1 | 48.3 | 48.0 |
| 10.0 | 80.00 | 20.2 | 60.67 | 47.6 | 47.8 | |
| 15.0 | 220.0 | 13.8 | 22.40 | 46.1 | 46.4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Friesen, S.; Hannappel, Y.; Kakorin, S.; Hellweg, T. Accounting for Cooperativity in the Thermotropic Volume Phase Transition of Smart Microgels. Gels 2021, 7, 42. https://doi.org/10.3390/gels7020042
Friesen S, Hannappel Y, Kakorin S, Hellweg T. Accounting for Cooperativity in the Thermotropic Volume Phase Transition of Smart Microgels. Gels. 2021; 7(2):42. https://doi.org/10.3390/gels7020042
Chicago/Turabian StyleFriesen, Simon, Yvonne Hannappel, Sergej Kakorin, and Thomas Hellweg. 2021. "Accounting for Cooperativity in the Thermotropic Volume Phase Transition of Smart Microgels" Gels 7, no. 2: 42. https://doi.org/10.3390/gels7020042
APA StyleFriesen, S., Hannappel, Y., Kakorin, S., & Hellweg, T. (2021). Accounting for Cooperativity in the Thermotropic Volume Phase Transition of Smart Microgels. Gels, 7(2), 42. https://doi.org/10.3390/gels7020042