Spatial Positioning and Operating Parameters of a Rotary Bell Sprayer: 3D Mapping of Droplet Size Distributions

Abstract

In this study, we evaluated the fundamental physical behavior during droplet formation and flow from a rotary bell spray in the absence of an electrostatic field. The impact of a wide range of operating parameters of the rotary bell sprayer, such as flow rates, rotational speeds, and spatial positioning, on droplet sizes and size distributions using a three-dimensional (3-D) mapping was studied. The results showed that increasing the rotational speed caused the Sauter mean diameter of the droplets to decrease while increasing flow rate increased the droplet sizes. The rotational speed effect, however, was dominant compared to the effect of flow rate. An increase in droplet size radially away from the cup was noted in the vicinity of the cup, nevertheless, as the lateral distances from the cup and rotational speed were increased, the droplet sizes within the flow field became more uniform. This result is of importance for painting industries, which are looking for optimal target distances for uniform painting appearance. Furthermore, the theoretical formulation was validated with experimental data, which provides a wider range of applicability in terms of environment and parameters that could be tested. This work also provides an abundance of measurements, which can serve as a database for the validation of future droplet disintegration simulations.

1. Introduction

The challenges faced in developing and implementing effective automotive coating processes are evident by research performed to develop new paint formulations [1], new applicator designs [2], and optimum operating parameters for coating apparatus [3,4]. Researchers have performed studies concerning the effect of the speed of the rotary bell atomizers on the evaporation of the fluid [5], shaping air holes effect on atomization for pneumatic atomizers [6], the transfer process for electrostatic spray coating [7], and non-Newtonian liquid with shear-thinning behavior [8]. Furthermore, a substantial amount of research has concentrated on simulating the effects of operating parameters on the performance of electrostatic rotary bell sprayers (ERBS) [9,10,11,12,13]. However, due to the limitations of using only computational techniques, it is preferred that experimental methods in conjunction with computational simulations be used to more fully understand the complex dynamics of spray processes [14,15]. This combined experimental plus computational approach is capable of defining modifications and improvements needed to achieve the highest transfer efficiency, to maintain acceptable costs and environmental impacts, and to meet, ultimately, consumer expectations of coating quality [16].

A primary focus of previous studies has been understanding the fundamental physical behavior of rotary bell atomizers and on formulating the fundamental equations that predict droplet sizes based on the liquid properties of the spray. For example, hydrodynamic concepts were introduced [17] to describe the disintegration process during droplet formation from a continuous liquid flow, as well as flow regimes and the parameters controlling spray development were studied [18]. Frost [19] reported criteria to enable prediction of whether an atomizer could produce droplets, ligaments, or sheets. Papanastasiou et al. studied Newtonian and non-Newtonian fluid considerations from fluid properties, such as surface tension, viscosity, and inertial factors [20]. High-speed rotary (4000–40,000 rpm) bell cup studies combined with considerations of fluid properties showed that ligaments at the edge of a bell would disintegrate into irregular shapes for low viscosity liquids, whereas regular-shaped ligaments were produced using higher viscosity fluids [21]. Different ERBS bell cup designs were also investigated [22], including a serrated one with waterborne metallic paint.

The experimental techniques in these investigations, including qualitative hydrodynamics, diffraction spectrometry, and short spark photography, were used to delineate the spray droplet size distributions and the fluid atomization mode at the edge of the bell. Optical diagnostic techniques, such as shadowgraphy high-speed imaging [23], have also been used to measure droplet diameters and distributions from different atomizers.

Furthermore, numerical simulations were performed to develop insight into air flows and spray droplet transport [24] that may point to improved transfer efficiencies and increased droplet speeds as an electrostatic field was increased. The simulations also addressed ERBS rotational speeds, cup geometries, and fluid flow rates, in addition to comparing the results to pneumatic atomizers and airless guns [25]. In general, for rotary bells, the Sauter mean diameter (SMD) of the spray droplets increased linearly with the increasing radius of a bell cup, while increasing the bell’s rotational speed decreased the homogeneity of droplet breakup. Experimental studies [14,15,26] have also postulated that increasing the liquid flow rate to a bell cup would lead to a transition from a jet breakup of the liquid to a turbulent disintegration.

In the present study, we investigated the operating parameters’ impact on sizes and size distributions of droplets from an ERBS with its electrostatic field turned off. A three-dimensional (3-D) mapping technique was used to assess the data as a factor of the interactions between the fluid flows and bell cup operating parameters. Although it is well documented that, for automotive coatings, the transfer efficiency depends, among other things, on droplet size and size distributions [27], Darwish et al. [28] have also shown that during liquid atomization from an ERBS, the smaller diameter droplets (<20 µm) closely followed the shaping airflow whereas the larger droplets did not. Hence, measurements of droplet diameters as a function of operating parameters of the ERBS were envisioned to offer additional, helpful insight into the spray flow field’s behaviors that may point to a fundamental understanding of how to further improve the operating conditions of ERBS.

2. Mathematical Formulation

Figure 1 shows a schematic of an inner cone surface in spherical coordinates used for the mathematical formulation in this section.

A simplified equations of fluid motion from a rotating disk can be obtained by starting with a differential parcel of fluid and identifying forces acting upon it [29], or by starting with the formalism of the Navier-Stokes Equations and neglecting terms through an order of magnitude analysis or simplifying assumptions [30,31]. Using a differential parcel of fluid approach in a spherical coordinate system and assuming a constant polar angle or half of the cone angle [29], the following differential Equation (1) is derived, which consists of a centrifugal force and a viscous force term, where:

$$\frac{{\partial }^2{v}_r}{r^2\partial {\theta }^2}=\frac{-\rho r{\omega }^2}{\mu }{\sin }^2\beta$$

(1)

$v_r$ is radial velocity, $r\theta$ is in the direction of film thickness perpendicular to the bell surface, $\rho$ is density, $\omega$ is angular velocity, $\mu$ is viscosity, and $\beta$ is the half-cone angle. After Equation (1) is integrated using no-slip and no-shear boundary conditions, Equation (2) is obtained. It describes the radial velocity as a function of location in the film. However, the film’s thickness is undetermined at this point and can be obtained by equating the volumetric liquid supply flow rate, Q, at any radial position to the integrated radial flow rate through an imaginary cylinder wall, as is shown in Equation (3). Here, h is the thickness perpendicular to the bell cup surface of an assumed thin liquid film.

$$v_r=\frac{\rho {\omega }^2{\sin }^2\beta }{\mu }\left(r_s^3{\theta }_s\theta -r^3\frac{{\theta }^2}{2}\right)$$

(2)

$$h=\sqrt[3]{\frac{3Q\mu }{2\pi \rho R^2{\omega }^2\sin \beta }}$$

(3)

The Coriolis force was neglected in the preceding radial momentum equations, which is a reasonable assumption if the angular velocity is large relative to fluid field velocities. Similar equations have been shown previously [32] when the half cone angle was β = 90°.

If the Coriolis force is not neglected, the radial and tangential equations of momentum conservation are as shown by Equation (4a,b) [30,31]. These were derived from the Navier-Stokes equations of an incompressible fluid, and were simplified by assuming steady-state, no gravity, no azimuthal derivatives, two dimensional flow limited to the radial and tangential directions, and approximately fully-developed flow in the radial direction. The boundary conditions of no-slip at the bell surface and no-shear at the fluid-air interface were also part of the assumptions.

$$\begin{gathered} -{\omega }^{2}r{\sin }^2\left(\beta \right)+2{v^{\prime }}_{\varphi }\omega \sin \left(\beta \right)=\frac{\nu }{r^2}\frac{{\partial }^2{v}_r}{\partial {\theta }^2}\left(a\right) \\ -2v_r\omega \sin \left(\beta \right)=\frac{v}{r^2}\frac{{\partial }^2{v^{\prime }}_{\varphi }}{\partial {\theta }^2}\left(b\right) \end{gathered}$$

(4)

Note that the prime in Equation (4) indicates the tangential velocity ${v^2}_{\varphi }$ is in rotating coordinates [30]. If Equation (4a,b) is cast into a non-dimensional form, the resultant equations are shown in Equation (5a,b). U $(v_r/\omega r\sin \beta )$ and W $({v^{\prime }}_{\varphi }/\omega r\sin \beta )$ are in the form of Rossby $(Vel/(\omega Len))$ numbers and the second derivative terms are in the form of approximate curvatures of Ekman $(Visc/\left(\omega Le{n}^2\right))$ numbers along the film’s thickness. The independent non-dimensional variable $s$ $\left(r\theta \sqrt{\omega \sin \beta /\nu }\right)$ is in the direction of the film’s thickness.

$$\begin{gathered} -1+2W=U^{″}\left(a\right) \\ -2U=W^{″}\left(b\right) \end{gathered}$$

(5)

The system of Equation (5) can be solved by substitution, thereby yielding a fourth-order differential equation. Another solution can be obtained if Equation (5b) is multiplied by $-i$, then summed with Equation (5a), along with the substitution $\psi =U-iW,$ resulting in the Equation (6), where $s^{\prime }$ is the non-dimensional thickness of the fluid [33]. The no-slip/no-shear boundary conditions are expressed as functions of Ψ.

$$\begin{gathered} {\psi }^{″}-2i\psi =-1 \\ \mathsf{\Psi }\left(s\right)=0,{\mathsf{\Psi }}^{\prime }\left(s^{\prime }\right)=0 \end{gathered}$$

(6)

The radial component of the solution to Equation (6) is shown as Equation (7).

$$\begin{gathered} \mathrm{U}=-\frac{1}{2}\sin \left(s\right)\sinh \left(s\right)+\frac{\sin \left(2s^{\prime }\right)\cos \left(s\right)\sinh \left(s\right)}{2(\cos \left(2s^{\prime }\right)+\cosh \left(2s^{\prime }\right)} \\ +\frac{\sinh \left(2s^{\prime }\right)\cosh \left(s\right)\sin \left(s\right)}{2\left(\cos \left(2s^{\prime }\right)+\cosh \left(2s^{\prime }\right)\right)} \end{gathered}$$

(7)

At the high RPM of an ERBS, the velocity profiles from Equation (7) become indistinguishable from those obtained from Equations (1)–(3). Therefore, at high RPM, the centrifugal force overwhelms the other forces, and coupling the equations did not yield additional mathematical insight. As a result, Equations (1)–(3) are sufficient for estimating the film’s thickness properties. Further increases in the sophistication of the mathematical modeling could be incorporated, for example, the use of transient behavior and boundary conditions that are more complex than the no-slip/no-shear assumptions. However, this type of sophistication is not necessary for describing film flow in an ERBS. The film will break up into ligaments at the edge of the cup. The number of ligaments is a function of the operating conditions, the fluid material properties, and cup serration design. In this experiment, the cup was serrated, which will control the number of ligaments, resulting in the ligament size (d_L) being directly proportional to the film height (h) and inversely proportional to the number of ligaments (N).

$$d_L\propto h/N$$

(8)

Those ligaments will break up into droplets in the primary breakup area, where the size of the droplet (D) is directly related to the ligament size.

$$D\propto d_L$$

(9)

From Equations (3), (8), and (9) the resultant droplets at the edge of the cup are a function of the fluid material properties (fluid viscosity (µ) and the Density (ρ)), cup design (Cup radius (R), and (β) and serration type along with the number of ligaments (N)), and the operating conditions (fluid flow rate (Q) and the rotational speed ($\omega$)). In this experiment, the fluid material properties and the cup design and serration type were kept constant, resulting in the droplets being a function of the process operating conditions namely the flow rate (Q) and the rotational speed ($\omega$).

$$D\propto f\left(\mu ,\rho \right)g(R,\sin \beta ,N)\sqrt[3]{\frac{Q}{{\omega }^2}}$$

(10)

3. Experimental Setup

3.1. Rotary Bell

Figure 2 shows a schematic of the experimental setup used for droplet size measurements. The ERBS (Durr eco-bell 2) had a bell cup radius of 3.25 cm and was connected to a Durr control unit that facilitated the control of shaping air flow rates and bell cup rotational speeds. For simplicity, water was used as a paint surrogate [3], and it was sprayed in a paint booth (Paasche FABSF horizontal draft spray booth) that pulled the droplets away from the measurement zone. The shaping air flow rate was fixed at 200 LPM for all experiments. The ERBS speed varied from 20 to 60 kRPM in 5 kRPM increments. Three different fluid flow rates were used, including 150 ccm, 250 ccm, and 350 ccm. The various operating parameters were tested at 17 different locations downstream of the cup, as shown in

Table 1. The measurement locations inside the spray flow field.

Horizontal Distance from Cup Edge (Streamwise Direction, Z) (Non-Dimensionalized with Cup Radius, R)	0.31R	0.92R	1.54R	3.08R	6.15R
Vertical Distance below Cup Center (Radial Direction, r) (non-dimeasionalized with cup radius, R)	0	0	0	0	0
	0.5R	-----	0.5R	-----	0.5R
	R	-----	R	-----	R
	1.5R	-----	1.5R	-----	1.5R
	2R	-----	2R	-----	2R

.

A Malvern Spraytec was used for droplet size measurements. It was placed on an optical table such that probing the spray envelope could be accomplished at different locations. It utilized a He–Ne, 633 nm laser beam for the diffraction measurements.

The spray from the ERBS was delivered between the transmitter and receiver modules of the Malvern Spraytec. The laser light, upon encountering droplets in the spray, was scattered and detected by the receiver module—smaller droplets cause larger scattering angles than do larger droplets. The Spraytec receiver had an array of 30 detectors that quantified scattered light intensity patterns, and the droplet size distributions were calculated based on the Mie theory. The use of water for the test simplified the application of the Mie theory for size determination analyses since water droplet property: density and refractive index, are known. Furthermore, the refractive index and density of the shaping air are also known. Due to the fact that Mie scattering assumes spherical droplets, which is not always the case, the Spraytec uses an equivalent sphere volumetric analysis in which the diameters of the spheres were represented through equivalent volumes of the droplets.

Background noise in the atmosphere with no spray is accounted for by the Spraytec instrument via measuring background scattering and then subtracting it from spray measurements to produce a corrected scattering intensity that ensures the patterns used for size determinations are solely a result of droplets in the spray. Finally, a built-in multiple scattering algorithm of the spraytec was enabled to account for multiple scattering of light by successive droplets through the spray and then applied to produce corrected scattering patterns. From the droplet size distributions, Sauter mean diameters (D₃₂) were calculated and used to characterize the spray. Each value of D₃₂ shown in the results is the average of 15 readings, which were taken at each point.

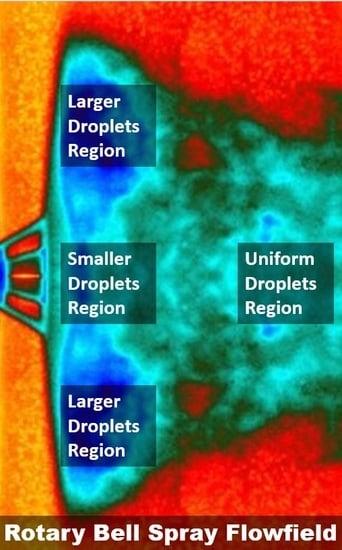
3.2. Infrared Thermography Visualization

The infrared camera used to capture the spray field is a FLIR ThermoVision^TM SC4000 (FLIR, Wilsonville, OR, USA), with a cooled Indium Antimonide (InSb) type detector, having a 3–5 µm spectral range and a 320 × 256 pixel detector size. The detector was calibrated at an integration time of 2.0 ms and captured up to 400 frames at the full-frame size. The spatial pixel size was 1.083 mm.

The background radiation source used was an IR-160/301 Blackbody System (Infrared Systems Development, Winter Park, FL, USA); which was an extended area (30 cm × 30 cm) type flat plate emitter with special high emissivity coating having 0.96 (±0.02) average emissivity. The Black body temperature was set at 30 °C [34]. The experimental setup is shown in Figure 3.

4. Results and Discussion

4.1. Sauter Mean Diameter Analysis

Fluid (water) flow rates and rotational speeds of the rotary bell were varied during the tests as the light scattering intensities were measured at different vertical and horizontal locations within the spray flow field. A schematic of the flows, bell cup, resultant flow fields, along with an infrared image taken during the spray tests, are presented in Figure 4.

The spray droplets were formed at the edge of the bell cup and primarily followed an initial radial trajectory because of the centrifugal force used in generating them (Figure 4a). The presence of shaping air then changed the trajectory of the droplets depending on the competing factors of droplet inertia and shaping air forces [35]. Radial travel distances of the droplets were reduced with increasing bell cup rotational speed as a consequence of smaller droplets being formed, i.e., the inertia of larger particles is higher and resists the momentum forces of the shaping airflow. As droplet sizes were reduced with increasing bell cup rotational speeds, as can be noted within the factors contained in Equation (3), they became more affected by the shaping airflow [30,35], and their radial travel distances were curtailed.

The infrared image in Figure 4c depicts a map of radiant flux per unit surface area (W/m²) using the following equation:

$$E=\epsilon \sigma T^4$$

(11)

where ε is the emissivity of the blackbody background (0.96), σ is the Stefan–Boltzmann constant (5.670 × 10⁻⁸ W/m² K⁴), and T is the temperature measured by the infrared camera (degrees Kelvin). Blue color represents a relatively cold temperature as compared to the background temperature in red.

The flow lines depicted in Figure 4b, and the IR images in Figures 5, 7, and 9, imply that the high-speed rotary bell atomizer produced an axisymmetric spray with cross-sections having ‘donut’ shapes, i.e., lower concentrations of droplets existed close to the central axis of bell cup in comparison to the peripheral edges of the bell cup [35]. This ‘donut’ spray pattern is the result of a toroid-shaped ring formed by the interaction between the liquid droplets and the shaping airflow [35] as the high-speed liquid flow interacted with the high-speed shaping airflow, i.e., the liquid droplets and the shaping air impinged onto each other in nearly perpendicular directions. This vortex motion then formed the toroid-shaped ring, which momentary traps larger droplets [34] and, hence, increased droplet concentrations away from the lateral axis.

The flow lines depicted in Figure 4b, and the IR images in Figures 5, 7, and 9, imply that the high-speed rotary bell atomizer produced an axisymmetric spray with cross-sections having ‘donut’ shapes, i.e., lower concentrations of droplets existed close to the central axis of bell cup in comparison to the peripheral edges of the bell cup [35]. This ‘donut’ spray pattern is the result of a toroid-shaped ring formed by the interaction between the liquid droplets and the shaping airflow [35] as the high-speed liquid flow interacted with the high-speed shaping airflow, i.e., the liquid droplets and the shaping air impinged onto each other in nearly perpendicular directions. This vortex motion then formed the toroid-shaped ring, which momentary traps larger droplets [34] and, hence, increased droplet concentrations away from the lateral axis.

4.1.1. Three-Dimensional Analysis of Droplet Size, Bell Speed, Spatial Location within the Spray Flow Field along the Radial Direction at a Fluid Flow Rate of 150 ccm

Figure 5a presents an infrared image of the spray flow field during testing and contains dimensional locations at which laser scattering measurements were accomplished while measuring spray droplet sizes. These locations were normalized relative to the bell cup radius, R. Before each data acquisition test using the Spraytec, bell cup rotational speeds were set at predetermined values between 20–60 kRPM. The SMD, D₃₂ droplet diameters were calculated and plotted in a 3D representation shown in Figure 5b–d, with each Figure representing a fixed lateral distance of 0.31R, 1.54R, or 6.15R from the sprayer, respectively, while radial measurement distances varied between 0R-to-2R. At each radial and lateral position, increased rotational cup speeds significantly decreased droplet size. The increase in rotational speed resulted in higher centrifugal accelerations of the droplets, leading to higher associated inertia. The increase in inertia to surface tension forces, leads to the breakup of larger droplets, as they become unstable at high Weber numbers. However, only small changes in droplet diameters were measured from the center of the cup towards its edge, i.e., in the radial direction. Larger droplets, having more inertia in the tangential direction than smaller droplets, tend to resist shaping air interaction more, which explains the increase in the Sauter mean diameter, D₃₂ towards the edge of the cup compared to the center. This can be observed in Figure 5b. However, this effect tends to fade in measured droplet sizes downstream in the lateral direction, as can be seen in Figure 5c,d, and the droplets’ sizes become more uniform in the radial direction, i.e., there is no effect of the radial direction on the droplet size as we move away from the cup.

For better visualization of this phenomena, Figure 6 represents a cut through the 3D map at three different rotational speeds was plotted along with the standard deviation of the measurements’ data plotted as error bars on the graph. Figure 6a data were acquired at Z = 0.31R, Figure 6b at Z = 1.54R, and Figure 6c at Z = 6.15R. It can be observed that a location of Z = 6.15R (or 20 cm) is the average industry target distance ERBS’s paint application. It is noted in Figure 6a that moving radially away from the edge of the cup and outwards, i.e., from one to two radial distances from the center of the cup, the droplet size is increasing, a result of the higher inertia of the larger droplets and therefore higher resistance to the shaping air. However, moving in the lateral direction, that is Figure 6b,c we see that the radial direction does not have a determinant impact on the droplet size, as all the larger droplets have moved radially near the edge of the cup, and only smaller droplets followed the direction of the shaping air. It is also worth noting in Figure 6 that the error bars representing the standard deviation of the measurements, which decreases with increasing rotational speeds, this result is particularly important as the generation of more uniform droplet size is usually required by painting industries.

4.1.2. Three-Dimensional Analysis of Droplet Size, Bell Speed, Spatial Location within the Spray Flow Field along Radial Direction at Fluid Flow Rate of 250 ccm

Figure 7 and Figure 8 show experimental data similar to those in Figure 5 and Figure 6 except that the fluid flow rate was increased to 250 ccm.

The data trends in Figure 7 and Figure 8 were the same as those shown in Figure 5 and Figure 6 when the fluid flow rate was 150 ccm, i.e., higher bell cup rotational speeds decreased D₃₂ values at all locations measured within the flow field and effect of radial position on variations of D₃₂ were smaller compared to rotational speed effects. However, the overall average droplet diameters at a 250 ccm flow rate were slightly larger than the corresponding values at 150 ccm due to the increased amount of liquid fed to the atomizer, which in turn increased the film’s thickness and therefore ligament and droplet sizes, this is further discussed in the following sections.

In Figure 7b, we observed that droplets’ size in the vicinity of the cup increased in size at higher radial distances but is almost uniform at higher rotational speeds. Figure 8a is a clear demonstration of that behavior. We again see the same trend in Figure 7c–d and Figure 8b–c as those in the previous section. At larger distances from the cup, the effect of radial distance is insignificant, and the rotational speed plays the dominant role in determining the size of the droplets and the droplet distribution. It is also noted that the span of the average measurement of the D₃₂ represented by the standard deviation on Figure 8, is decreased with increasing speeds for all the different operating parameters, asserting the fact that the higher rotational speed essentially enhances the size uniformity of the generated droplets.

4.1.3. Three Dimensional Analysis of Droplet Size, Bell Speed, Spatial Location within the Spray Flow Field along Radial Direction at Fluid Flow Rate of 350 ccm

Figure 9 is similar to Figure 5 and Figure 7, except that the fluid flow rate was increased to 350 ccm. The trends in Figure 9 agree with the previous section. Higher cup rotational speeds decreased D₃₂ values at all locations measured within the flow field, dominating the effect of radial positions. The trend of droplets’ size near the cup observed in Figure 9b and Figure 10a was similar to that of Figure 7b and Figure 8a, i.e., droplets size increases as away from the edge of the cup radially outwards at lower rotational speeds. At larger distance downstream, Figure 9b,c we see that the effect of radial direction on droplet size is insignificant and only rotational speed plays a dominant role in the droplet size. We can also see that higher rotations speed generate more uniform droplets in all the cases presented in Figure 10. Comparing the overall average droplet diameters at a 350 ccm flow rate were slightly larger than the corresponding values at 150 or 250 ccm because of the increased amount of liquid fed to the atomizer. Figure 11 shows the effect of flow rate on droplet size distribution at a fixed rotational speed of 35 kRPM. We can see a slight shift towards higher droplets diameters as the fluid flow rate was increased.

4.1.4. Three-Dimensional Analysis of Droplet Size, Bell Speed, Spatial Location within the Spray Flow Field along Streamwise Flow Direction at a Variable Fluid Flow Rate

In the following part of this work, D₃₂ was investigated for different bell cup rotational speeds and different mass flow rate of fluid and at different lateral locations away from the cup. Figure 12a–c presents the D₃₂ values at different horizontal locations at fluid flowrates of 150 ccm, 250 ccm, and 350 ccm, respectively, and by varying the rotational speed of the cup.

Figure 13a–c also represents the same D₃₂ values but in two-dimensional representationwith standard deviation associated with D₃₂ readings shown, at flow rates of 150 ccm, 250 ccm, and 350 ccm, respectively, and varying the rotational speed.

Figure 12 shows that droplet size decreased with the increase in the cup’s rotational speed whereas droplet size increased with the increase in fluid flow rate all around in lateral locations, this can also be seen in Figure 13. The uniform droplets were formed along the lateral positions at higher rotational speed as standard deviations decreased despite the change in fluid flow rate. Thus, droplet size was more influenced by the rotational speed of the cup compared to the fluid flow rate. This can also be observed by Equations (3) and (10), and is further explained in the next section.

4.1.5. Comparison between Theoretical model and Experimental Data of the SMD

Figure 14 shows that the relationship between the SMD and the film thickness is linear as predicted by Equation (10). Linear regression was used to fit the overall data (black line), and individual data sets of 150 ccm (circles), 250 ccm (triangle), and 350 ccm (squares) the slopes were found to be 0.1678 ± 0.0030, 0.2017 ± 0.0029, 0.2056 ± 0.0033, and 0.1742 ± 0.0019. Statistical treatment using Two-way ANOVA with Sidak comparison tests of the data showed that the changes in the slope are statistically insignificant between all cases. These results suggest that the height of the liquid film h inside the cup controls the droplet sizes. This can be explained by the fact that the film thickness directly impacts the size of the ligaments formed at the cup edge, which is linearly related to the droplet size [36]. Since the film’s thickness is inversely proportional to ω^2/3 and proportional to Q^1/3, the rotational speed has a higher impact on the film thickness compared to the flow rate, which in turn is translated into a higher impact on the generated droplet size, as confirmed by experimental results.

5. Conclusions

In this study, the effects of fluid flow rates and rotational speeds of a rotary bell sprayer on spray droplet size distributions in radial and lateral directions from the cup were investigated. A three-dimensional map presenting the data was then created, which provided a visual image of the effect of multiple operating parameters simultaneously. Droplet behaviors near the bell cup were different from those further away from the cup in all directions measured. At the cup, forces from the centrifugal action as droplets were formed at the edge of the rotating cup compete with the forces of the shaping airflow, which was perpendicular to the cup edge. Since the inertia of the droplets changes as their diameters change, the droplet trajectories became a function of droplet inertia and shaping air forces. Hence, radial travel distances of the droplets were decreased with increasing bell cup rotational speeds because the droplet sizes became smaller. However, as lateral distances were increased to about 1.5–6 times the radius of the cup, and the rotational speeds were increased, the concentrations within the spray flow field were more uniform. This behavior influences how close a bell cup can be placed near a target surface and still maintain uniform droplet concentrations within the spray field at the target, resulting in quality coating finish.

Furthermore, validation of theoretical formulations was provided by comparing them to experimental results. This is particularly important because theoretical formulations are more general and can be applied to a variety of environments and parameters. The experimentations provide a rich validation database for researchers carrying out atomization simulations in the future. The paper provides insight for the spraying industries, on how to achieve required droplet size distribution by manipulating the different operating parameters and target distance from the spray applicator.