Cloud-Based CAD Parametrization for Design Space Exploration and Design Optimization in Numerical Simulations
Abstract
:1. Introduction
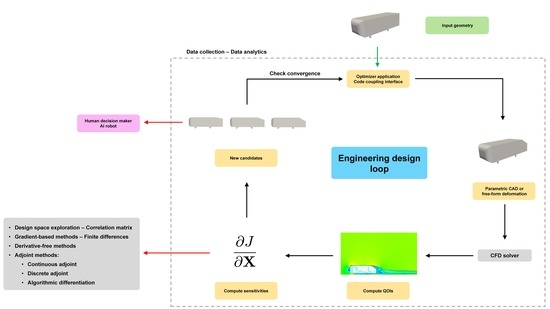
2. Description of the Workflow—Methodology
3. Numerical Experiments
3.1. Cylinder Optimization Problem—Minimum Surface and Fixed Volume
| Listing 1. Excerpt of the Python code used to setup the parametric configuration variables. |
 |
| Listing 2. Excerpt of the Python code used to evaluate the measurements. |
 |
3.2. Static Mixer Optimization Case
3.3. Two Ahmed Bodies in Platoon
4. Conclusions and Future Perspectives
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A

References
- Mattson, C.A. Design Exploration. Available online: https://design.byu.edu/blog/design-exploration-presentation-given-stanford-university-15-jan-2014 (accessed on 22 February 2020).
- Forrester, A.; Sobester, A.; Keane, A. Engineering Design via Surrogate Modeling. A Practical Guide; Wiley: Hoboken, NJ, USA, 2008. [Google Scholar]
- Guerrero, J.; Cominetti, A.; Pralits, J.; Villa, D. Surrogate-Based Optimization Using an Open-Source Framework: The Bulbous Bow Shape Optimization Case. Math. Comput. Appl. 2018, 23, 60. [Google Scholar] [CrossRef] [Green Version]
- Romero, V.J.; Swiler, L.P.; Giunta, A.A. Construction of response surfaces based on progressive lattice-sampling experimental designs. Struct. Saf. 2004, 26, 201–219. [Google Scholar] [CrossRef]
- Kochenderfer, M.; Wheeler, T. Algorithms for Optimization; MIT Press: Cambridge, MA, USA, 2019. [Google Scholar]
- Gen, M.; Cheng, R. Genetic Algorithms and Engineering Optimization; Wiley-Interscience: Hoboken, NJ, USA, 2000. [Google Scholar]
- Vanderplaats, G. Multidiscipline Design Optimization; Vanderplaats Research & Development, Inc.: Colorado Springs, CO, USA, 2007. [Google Scholar]
- Papalambros, P.; Wilde, D. Principles of Optimal Design. Modeling and Computation; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
- Nocedal, J.; Wright, S. Numerical Optimization; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Chong, E.; Zak, S. An Introduction to Optimization; Wiley: Hoboken, NJ, USA, 2013. [Google Scholar]
- Sobieszczanski-Sobieski, J.; Morris, A.; van Tooren, M.; Rocca, G.L.; Yao, W. Multidisciplinary Design Optimization Supported by Knowledge Based Engineering; Wiley: Hoboken, NJ, USA, 2015. [Google Scholar]
- Chauhan, S.; Hwang, J.; Martins, J. An automated selection algorithm for nonlinear solvers in MDO. Struct. Multidiscip. Optim. 2018, 58, 349–377. [Google Scholar] [CrossRef] [Green Version]
- Martins, J. The adjoint method in multidisciplinary design optimization—Special session in honor of Antony Jameson’s 85th birthday. In Proceedings of the AIAA SciTech Forum, Nashville, TN, USA, 6 January 2020. [Google Scholar]
- Vassberg, J.C.; Jameson, A. Introduction to Optimization and Multidisciplinary Design Part I: Theoretical Background for Aerodynamic Shape Optimization; Lecture Series March 2016; Von Karman Institute: Brussels, Belgium, 2016. [Google Scholar]
- Keane, A.J.; Nair, P.B. Computational Approaches for Aerospace Design: The Pursuit of Excellence; John Wiley & Sons: Hoboken, NJ, USA, 2005. [Google Scholar]
- Martins, J.R.R.A.; Lambe, A.B. Multidisciplinary Design Optimization: A Survey of Architectures. AIAA J. 2013, 51, 2049–2075. [Google Scholar] [CrossRef] [Green Version]
- The OpenFOAM Foundation. Available online: http://www.openfoam.org (accessed on 22 February 2020).
- Weller, H.G.; Tabor, G.; Jasak, H.; Fureby, C. A tensorial approach to computational continuum mechanics using object-oriented techniques. Comput. Phys. 1998, 12, 620–631. [Google Scholar] [CrossRef]
- Dakota Web Page. 2018. Available online: https://dakota.sandia.gov/ (accessed on 22 February 2020).
- Adams, B.M.; Eldred, M.S.; Geraci, G.; Hooper, R.W.; Jakeman, J.D.; Maupin, K.A.; Monschke, J.A.; Rushdi, A.A.; Stephens, J.A.; Swiler, L.P.; et al. Dakota, a Multilevel Parallel Object-Oriented Framework for Design Optimization, Parameter Estimation, Uncertainty Quantification, and Sensitivity Analysis: Version 6.10 User Manual; Sandia National Laboratories: Albuquerque, NM, USA, 2019. [Google Scholar]
- The Visualization Toolkit (VTK). Available online: http://www.vtk.org (accessed on 22 February 2020).
- Onshape Product Development Platform. Available online: http://www.onshape.com (accessed on 22 February 2020).
- Slotnick, J.; Khodadoust, A.; Alonso, J.; Darmofal, D.; Gropp, W.; Lurie, E.; Mavriplis, D. CFD Vision 2030 Study: A Path To Revolutionary Computational Aerosciences; Technical Report; NASA: Hampton, VA, USA, 2014.
- Daymo, E.; Tonkovich, A.L.; Hettel, M.; Guerrero, J. Accelerating reactor development with accessible simulation and automated optimization tools. Chem. Eng. Process. Process Intensif. 2019, 142, 107582. [Google Scholar] [CrossRef]
- Xia, C.C.; Gou, Y.J.; Li, S.H.; Chen, W.F.; Shao, C. An Automatic Aerodynamic Shape Optimisation Framework Based on DAKOTA. IOP Conf. Ser. Mater. Sci. Eng. 2018, 408, 012021. [Google Scholar] [CrossRef]
- Byrne, J.; Cardiff, P.; Brabazon, A.; O’Neill, M. Evolving parametric aircraft models for design exploration. J. Neurocomput. 2014, 142, 39–47. [Google Scholar] [CrossRef]
- Ohm, A.; Tetursson, H. Automated CFD Optimization of a Small Hydro Turbine for Water Distribution Networks; Technical Report; Chalmers University of Technology: Göteborg, Sweden, 2017. [Google Scholar]
- Sousa, J.; Gorlé, C. Computational urban flow predictions with Bayesian inference: Validation with field data. Build. Environ. 2019, 154, 13–22. [Google Scholar] [CrossRef]
- Kiani, H.; Karimi, F.; Labbafi, M.; Fathi, M. A novel inverse numerical modeling method for the estimation of water and salt mass transfer coefficients during ultrasonic assisted-osmotic dehydration of cucumber cubes. Ultrason. Sonochem. 2018, 44, 171–176. [Google Scholar] [CrossRef]
- Habla, F.; Fernandes, C.; Maier, M.; Densky, L.; Ferras, L.; Rajkumar, A.; Carneiro, O.; Hinrichsen, O.; Nobrega, J.M. Development and validation of a model for the temperature distribution in the extrusion calibration stage. Appl. Therm. Eng. 2016, 100, 538–552. [Google Scholar] [CrossRef]
- Khamlaj, T.A.; Rumpfkeil, M.P. Analysis and optimization of ducted wind turbines. Energy 2018, 162, 1234–1252. [Google Scholar] [CrossRef]
- Montoya, M.C.; Nieto, F.; Hernandez, S.; Kusano, I.; Alvarez, A.; Jurado, J. CFD-based aeroelastic characterization of streamlined bridge deck cross-sections subject to shape modifications using surrogate models. J. Wind Eng. Ind. Aerodyn. 2018, 177, 405–428. [Google Scholar] [CrossRef]
- Kelm, S.; Müller, H.; Hundhausen, A.; Druska, C.; Kuhr, A.; Allelein, H.J. Development of a multi-dimensional wall-function approach for wall condensation. Nucl. Eng. Des. 2019, 353, 110239. [Google Scholar] [CrossRef]
- Zoutendijk, G. Methods of Feasible Directions: A Study in Linear and Non-Linear Programming; Elsevier: Amsterdam, The Netherlands, 1960. [Google Scholar]
- Vanderplaats, G.N. An efficient feasible directions algorithm for design synthesis. AIAA J. 1984, 22, 1633–1640. [Google Scholar] [CrossRef]
- Le Digabel, S. Algorithm 909: NOMAD: Nonlinear Optimization with the MADS Algorithm. ACM Trans. Math. Softw. 2011, 37. [Google Scholar] [CrossRef]
- Guerrero, J. Opportunities and challenges in CFD optimization: Open Source technology and the Cloud. In Proceedings of the Sixth Symposium on OpenFOAM® in Wind Energy (SOWE), Göteborg, Sweden, 13–14 June 2018. [Google Scholar]
- Oliver, M.; Webster, R. Kriging: A Method of Interpolation for Geographical Information Systems. Int. J. Geogr. Inf. Syst. 1990, 4, 313–332. [Google Scholar] [CrossRef]
- Adams, B.M.; Eldred, M.S.; Geraci, G.; Hooper, R.W.; Jakeman, J.D.; Maupin, K.A.; Monschke, J.A.; Rushdi, A.A.; Stephens, J.A.; Swiler, L.P.; et al. Dakota, a Multilevel Parallel Object-Oriented Framework for Design Optimization, Parameter Estimation, Uncertainty Quantification, and Sensitivity Analysis: Version 6.10 Theory Manual; Sandia National Laboratories: Albuquerque, NM, USA, 2014.
- Dalbey, K.R.; Giunta, A.A.; Richards, M.D.; Cyr, E.C.; Swiler, L.P.; Brown, S.L.; Eldred, M.S.; Adams, B.M. Surfpack User’s Manual Version 1.1; Sandia National Laboratories: Albuquerque, NM, USA, 2013.
- Dalbey, K.R. Efficient and Robust Gradient Enhanced Kriging Emulators; Technical Report; Sandia National Laboratories: Albuquerque, NM, USA, 2013.
- Giunta, A.A.; Watson, L. A comparison of approximation modeling techniques: Polynomial versus interpolating models. In 7th AIAA/USAF/NASA/ISSMO Symposium on Multidisciplinary Analysis and Optimization; NASA Langley Technical Report Server: Hampton, VA, USA, 1998. [Google Scholar]
- Inselberg, A. Parallel Coordinates, Visual Multidimensional Geometry and Its Applications; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Pagliarella, R.M.; Watkins, S.; Tempia, A. Aerodynamic Performance of Vehicles in Platoons: The Influence of Backlight Angles. SAE World Congr. Exhib. SAE Int. 2007. [Google Scholar] [CrossRef]
- Pagliarella, R.M. On the Aerodynamic Performance of Automotive Vehicle Platoons Featuring Pre and Post-Critical Leading Forms; Technical Report; RMIT University: Melbourne, Austrialia, 2009. [Google Scholar]
- Sampat, M.P.; Wang, Z.; Gupta, S.; Bovik, A.C.; Markey, M.K. Complex wavelet structural similarity: A new image similarity index. IEEE Trans. Image Process. 2009, 18, 2385–2401. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image Quality Assessment: From Error Visibility to Structural Similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [Green Version]
- Eskicioglu, A.M.; Fisher, P.S. Image Quality Measures and Their Performance. IEEE Trans. Commun. 1995, 43, 2959–2965. [Google Scholar] [CrossRef] [Green Version]
- Ndajah, P.; Kikuchi, H.; Yukawa, M.; Watanabe, H.; Muramatsu, S. SSIM image quality metric for denoised images. In Proceedings of the International Conference on Visualization, Imaging and Simulation, Faro, Portugal, 3–5 November 2010; pp. 53–57. [Google Scholar]
- Lin, Y.; Chai, L.; Zhang, J.; Zhou, X. On-line burning state recognition for sintering process using SSIM index of flame images. In Proceedings of the 11th World Congress on Intelligent Control and Automation, Shenyang, China, 29 June–4 July 2014; pp. 2352–2357. [Google Scholar] [CrossRef]
- Priyal, S.P.; Bora, P.K. A study on static hand gesture recognition using moments. In Proceedings of the International Conference on Signal Processing and Communications (SPCOM), Bangalore, India, 18–21 July 2010; pp. 1–5. [Google Scholar] [CrossRef]
- Van der Walt, S.; Schönberger, J.L.; Nunez-Iglesias, J.; Boulogne, F.; Warner, J.D.; Yager, N.; Gouillart, E.; Yu, T. Scikit-image: Image processing in Python. PeerJ 2014, 2, e453. [Google Scholar] [CrossRef]















| MFD-1 | MFD-2 | Analytical Solution | |
|---|---|---|---|
| Starting point-Height (height_to_update)-cm | 4 | 2 | - |
| Starting point-Diameter (dia1_to_update)-cm | 8 | 12 | - |
| Optimal value-Height (height_to_update)-cm | 7.617 | 7.607 | 7.675 |
| Optimal value-Diameter (dia1_to_update)-cm | 7.692 | 7.697 | 7.674 |
| QoI ()- | 277.026 | 277.027 | 277.54 |
| Non-linear constraint (Volume)- | 354.001 | 354.000 | 354.98 |
| Function evaluations | 88 | 405 | - |
| MFD | MADS | Analytical Solution | |
|---|---|---|---|
| Optimal value-Height (height_to_update)-cm | 7.617 | 7.699 | 7.675 |
| Optimal value-Diameter (dia1_to_update)-cm | 7.692 | 7.655 | 7.674 |
| QoI ()- | 277.026 | 277.236 | 277.54 |
| Non-linear constraint (Volume)- | 354.001 | 354.406 | 354.98 |
| Function evaluations | 88 | 256 | - |
| MFD-2DV | MFD-3DV | Analytical Solution | |
|---|---|---|---|
| Starting point-Height (height_to_update)-cm | 4 | 4 | - |
| Starting point-Diameter 1 (dia1_to_update)-cm | 8 | 8 | - |
| Starting point-Diameter 2 (dia2_to_update)-cm | - | 5 | - |
| Optimal value-Height (height_to_update)-cm | 7.617 | 7.648 | 7.675 |
| Optimal value-Diameter 1 (dia1_to_update)-cm | 7.692 | 7.686 | 7.674 |
| Optimal value-Diameter 2 (dia2_to_update)-cm | - | 7.666 | - |
| QoI ()- | 277.026 | 277.026 | 277.54 |
| Non-linear constraint (Volume)- | 354.001 | 354.004 | 354.98 |
| Function evaluations | 88 | 114 | - |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guerrero, J.; Mantelli, L.; Naqvi, S.B. Cloud-Based CAD Parametrization for Design Space Exploration and Design Optimization in Numerical Simulations. Fluids 2020, 5, 36. https://doi.org/10.3390/fluids5010036
Guerrero J, Mantelli L, Naqvi SB. Cloud-Based CAD Parametrization for Design Space Exploration and Design Optimization in Numerical Simulations. Fluids. 2020; 5(1):36. https://doi.org/10.3390/fluids5010036
Chicago/Turabian StyleGuerrero, Joel, Luca Mantelli, and Sahrish B. Naqvi. 2020. "Cloud-Based CAD Parametrization for Design Space Exploration and Design Optimization in Numerical Simulations" Fluids 5, no. 1: 36. https://doi.org/10.3390/fluids5010036
APA StyleGuerrero, J., Mantelli, L., & Naqvi, S. B. (2020). Cloud-Based CAD Parametrization for Design Space Exploration and Design Optimization in Numerical Simulations. Fluids, 5(1), 36. https://doi.org/10.3390/fluids5010036