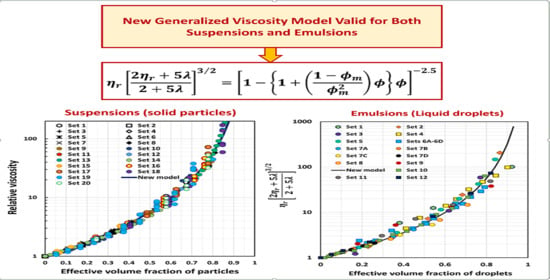
New Generalized Viscosity Model for Non-Colloidal Suspensions and Emulsions
Abstract
:1. Introduction
2. Viscosity Models for Suspensions of Non-Brownian Hard Spheres
2.1. Infinitely Dilute Suspensions
2.2. Non-Dilute Suspensions
3. New Approach to Modelling the Viscosity of Suspensions of Non-Brownian Hard Spheres
4. Comparison of Experimental Suspension Viscosity Data with Model Predictions
5. Viscosity Models for Emulsions of Non-Brownian Spherical Droplets
5.1. Infinitely Dilute Emulsions
5.2. Non-Dilute Emulsions
6. Comparison of Experimental Emulsion Viscosity Data with Proposed Model Predictions
7. Conclusions
Funding
Conflicts of Interest
Appendix A. Derivation of Equation (44)
References
- Pal, R. Rheology of Particulate Dispersions and Composites; CRC Press: Boca Raton, FL, USA, 2007. [Google Scholar]
- Pal, R. Fundamental Rheology of Disperse Systems Based on Single-Particle Mechanics. Fluids 2016, 1, 40. [Google Scholar] [CrossRef]
- Guth, E.; Simha, R. Untersuchungen über die Viskosität von Suspensionen und Lösungen. 3. Über die Viskosität von Kugelsuspensionen. Kolloid Z. 1936, 74, 266–275. [Google Scholar] [CrossRef]
- Saito, N. Concentration Dependence of the Viscosity of High Polymer Solutions. I. J. Phys. Soc. Jpn. 1950, 5, 4–8. [Google Scholar] [CrossRef]
- Vand, V. Viscosity of Solutions and Suspensions. I. Theory. J. Phys. Colloid Chem. 1948, 52, 277–299. [Google Scholar] [CrossRef] [PubMed]
- Manley, R.S.J.; Mason, S.G. The viscosity of suspensions of spheres: A note on the particle interaction coefficient. Can. J. Chem. 1954, 32, 763–767. [Google Scholar] [CrossRef]
- Batchelor, G.K.; Green, J.T. The determination of the bulk stress in a suspension of spherical particles to order c 2. J. Fluid Mech. 1972, 56, 401. [Google Scholar] [CrossRef]
- Pal, R. Viscosity-Concentration relationships for nanodispersions based on glass transition point. Can. J. Chem. Eng. 2017, 95, 1605–1614. [Google Scholar] [CrossRef]
- Pal, R. Rheology of emulsions containing polymeric liquids. In Encyclopedia of Emulsion Technology; Becher, P., Ed.; Marcel Dekker: New York, NY, USA, 1996; Volume 4, pp. 93–263. [Google Scholar]
- Pal, R. Rheology of simple and multiple emulsions. Curr. Opin. Colloid Interface Sci. 2011, 16, 41–60. [Google Scholar] [CrossRef]
- Roscoe, R. The viscosity of suspensions of rigid spheres. Br. J. Appl. Phys. 1952, 3, 267–269. [Google Scholar] [CrossRef]
- Brinkman, H.C. The Viscosity of Concentrated Suspensions and Solutions. J. Chem. Phys. 1952, 20, 571–581. [Google Scholar] [CrossRef]
- Mooney, M. The viscosity of a concentrated suspensions of spherical particles. J. Colloid Sci. 1951, 6, 162–170. [Google Scholar] [CrossRef]
- Krieger, I.M.; Dougherty, T.J. Mechanism for non-Newtonian flow in suspensions of rigid particles. Trans. Soc. Rheol. 1959, 3, 137–152. [Google Scholar] [CrossRef]
- Simha, R. A Treatment of the Viscosity of Concentrated Suspensions. J. Appl. Phys. 1952, 23, 1020. [Google Scholar] [CrossRef]
- Happel, J. Viscosity of Suspensions of Uniform Spheres. J. Appl. Phys. 1957, 28, 1288. [Google Scholar] [CrossRef]
- Frankel, N.A.; Acrivos, A. On the viscosity of a concentrated suspension of solid spheres. Chem. Eng. Sci. 1967, 22, 847–853. [Google Scholar] [CrossRef]
- Graham, A.L. On the viscosity of suspensions of solid spheres. Appl. Sci. Res. 1981, 37, 275–286. [Google Scholar] [CrossRef]
- Thomas, D.G. Transport characteristics of suspension: VIII. A note on the viscosity of Newtonian suspensions of uniform spherical particles. J. Colloid Sci. 1965, 20, 267–277. [Google Scholar] [CrossRef]
- Maron, S.H.; Pierce, P.E. Application of Ree-Eyring generalized flow theory to suspensions of spherical particles. J. Colloid Sci. 1956, 11, 80–95. [Google Scholar] [CrossRef]
- Quemada, D. Rheology of concentrated disperse systems and minimum energy dissipation principle: 1. Viscosity-concentration relationship. Rheol. Acta 1977, 16, 82–94. [Google Scholar] [CrossRef]
- Mendoza, C.I.; Santamaria-Holek, I. The rheology of hard sphere suspensions at arbitrary volume fractions: An improved differential viscosity model. J. Chem. Phys. 2009, 130, 44904. [Google Scholar] [CrossRef] [Green Version]
- Faroughi, S.A.; Huber, C. A generalized equation for rheology of emulsions and suspensions of deformable particles subjected to simple shear flow at low Reynolds number. Rheol. Acta 2015, 54, 85–108. [Google Scholar] [CrossRef]
- Van den Temple, M. Effect of droplet flocculation on emulsion viscosity. In Rheology of Emulsions; Sherman, P., Ed.; Pergamon Press Ltd.: Oxford, UK, 1963. [Google Scholar]
- Gillespie, T. The effect of concentration on the viscosity of suspensions and emulsions. In Rheology of Emulsions; Sherman, P., Ed.; Pergamon Press Ltd.: Oxford, UK, 1963. [Google Scholar]
- Graham, A.L.; Bird, R.B. Particle clusters in concentrated suspensions. 1. Experimental observations of particle clusters. Ind. Eng. Chem. Fundam. 1984, 23, 406–410. [Google Scholar] [CrossRef]
- Pal, R. A new model for the viscosity of asphaltene solutions. Can. J. Chem. Eng. 2015, 93, 747–755. [Google Scholar] [CrossRef]
- Pal, R. Rheology of suspensions of solid particles in power-law fluids. Can. J. Chem. Eng. 2015, 93, 166–173. [Google Scholar] [CrossRef]
- Pal, R. Electromagnetic, Mechanical, and Transport Properties of Composite Materials; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Pal, R. Porosity-Dependence of Effective Mechanical Properties of Pore-Solid Composite Materials. J. Compos. Mater. 2005, 39, 1147–1158. [Google Scholar] [CrossRef]
- Pal, R. On the Electrical Conductivity of Particulate Composites. J. Compos. Mater. 2007, 41, 2499–2511. [Google Scholar] [CrossRef]
- Pal, R. Thermal conductivity of three-component composites of core-shell particles. Mater. Sci. Eng. A 2008, 498, 135–141. [Google Scholar] [CrossRef]
- Pal, R. New Models for the Viscosity of Nanofluids. J. Nanofluids 2014, 3, 260–266. [Google Scholar] [CrossRef]
- Vand, V. Viscosity of solutions and suspensions. II. Experimental determination of the viscosity-concentration function of spherical inclusions. J. Phys. Colloid Chem. 1948, 52, 300–314. [Google Scholar] [CrossRef] [PubMed]
- Ward, S.G.; Whitmore, R.L. Studies of the viscosity and sedimentation of suspensions Part 1—The viscosity of suspension of spherical particles. Br. J. Appl. Phys. 1950, 1, 286–290. [Google Scholar] [CrossRef]
- Lewis, T.B.; Nielsen, L.E. Viscosity of Dispersed and Aggregated Suspensions of Spheres. J. Rheol. 1968, 12, 421–443. [Google Scholar] [CrossRef]
- Rutgers, I.R. Relative viscosity of suspensions of rigid spheres in Newtonian liquids. Rheol. Acta 1962, 2, 202–210. [Google Scholar] [CrossRef]
- Ting, A.P.; Luebbers, R.H. Viscosity of suspensions of spherical and other isodimensional particles in liquids. AIChE J. 1957, 3, 111–116. [Google Scholar] [CrossRef] [Green Version]
- Zarraga, I.E.; Hill, D.A.; Leighton, D.T. The characterization of the total stress of concentrated suspensions of noncolloidal spheres in Newtonian fluids. J. Rheol. 2000, 44, 185–220. [Google Scholar] [CrossRef]
- Tanner, R.I.; Qi, F.; Dai, S. Scaling the normal stresses in concentrated non-colloidal suspensions of spheres. Rheol. Acta 2013, 52, 291–295. [Google Scholar] [CrossRef]
- Chong, J.S.; Christiansen, E.B.; Baer, A.D. Rheology of concentrated suspensions. Trans. Soc. Rheol. 1968, 12, 281–301. [Google Scholar] [CrossRef]
- Ilić, V.; Phan-Thien, N. Viscosity of concentrated suspensions of spheres. Rheol. Acta 1994, 33, 283–291. [Google Scholar] [CrossRef]
- Smith, J.H. Rheology of Concentrated Suspensions of Spheres. Ph.D. Thesis, California Institute of Technology, Pasadena, CA, USA, 1972. [Google Scholar]
- Pal, R. Comment on “Effective thermal conductivity of metal and non-metal particulate composites with interfacial thermal resistance at high volume fraction of nano to macro-sized spheres”. J. Appl. Phys. 2015, 117, 216101. [Google Scholar] [CrossRef]
- Taylor, G.I. The viscosity of a fluid containing small drops of another liquid. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1932, 138, 41–48. [Google Scholar] [CrossRef]
- Oldroyd, J.G. The elastic and viscous properties of emulsions and suspensions. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1953, 218, 122–132. [Google Scholar] [CrossRef]
- Yaron, I.; Gal-Or, B. On viscous flow and effective viscosity of concentrated suspensions and emulsions. Rheol. Acta 1972, 11, 241–252. [Google Scholar] [CrossRef]
- Choi, S.J.; Schowalter, W.R. Rheological properties of nondilute suspensions of deformable particles. Phys. Fluids 1975, 18, 420–427. [Google Scholar] [CrossRef]
- Pal, R. Novel viscosity equations for emulsions of two immiscible liquids. J. Rheol. 2001, 45, 509–520. [Google Scholar] [CrossRef]
- Pal, R. Single-Parameter and Two-Parameter Rheological Equations of State for Nondilute Emulsions. Ind. Eng. Chem. Res. 2001, 40, 5666–5674. [Google Scholar] [CrossRef]
- Pal, R. Rheological properties of emulsions of oil in aqueous non-newtonian polymeric media. Chem. Eng. Commun. 1992, 111, 45–60. [Google Scholar] [CrossRef]
- Pal, R. Rheology of polymer-thickened emulsions. J. Rheol. 1992, 36, 1245–1259. [Google Scholar] [CrossRef]
- Hsieh, I.T.G. On-Line Viscosity Measurement of Emulsions. Master’s Thesis, University of Waterloo, Waterloo, ON, Canada, 2000. [Google Scholar]
- Pal, R. Emulsions: Pipeline Flow Behavior, Viscosity Equations, and Flow Measurement. Ph.D. Thesis, University of Waterloo, Waterloo, ON, Canada, 1987. [Google Scholar]
- Pal, R. Shear viscosity behavior of emulsions of two immiscible liquids. Colloid Interface Sci. 2000, 225, 359–366. [Google Scholar] [CrossRef]
- Leviton, A.; Leighton, A. Viscosity Relationships in Emulsions Containing Milk Fat. J. Phys. Chem. 1936, 40, 71–80. [Google Scholar] [CrossRef]
- Bains, U. In-Situ Continuous Monitoring of Catastrophic Phase Inversion and Viscosity of Pickering Emulsions. Master’s Thesis, University of Waterloo, Waterloo, ON, Canada, 2018. [Google Scholar]
- Buhidma, A. Flow Measurement of Two-Phase Oil-In-Water Emulsions Using Wedge Meters and Segmental Orifice Meters. Master’s Thesis, University of Waterloo, Waterloo, ON, Canada, 1995. [Google Scholar]
- Wolf, B.; Lam, S.; Kirkland, M.; Frith, W.J. Shear thickening of an emulsion stabilized with hydrophilic silica particles. J. Rheol. 2007, 51, 465. [Google Scholar] [CrossRef]
- Pal, R. Viscoelastic properties of polymer-thickened oil-in-water emulsions. Chem. Eng. Sci. 1996, 51, 3299–3305. [Google Scholar] [CrossRef]
- Pal, R. Multiple O/W/O Emulsion Rheology. Langmuir 1996, 12, 2220–2225. [Google Scholar] [CrossRef]
- Sibree, J.O. The viscosity of emulsions—Part 1. Trans. Faraday Soc. 1930, 104, 26–36. [Google Scholar] [CrossRef]
- Broughton, G.; Squires, L. The viscosity of oil-water emulsions. J. Phys. Chem. 1938, 42, 253–263. [Google Scholar] [CrossRef]
- Pal, R. Rheological behaviour of surfactant-flocculated water-in-oil emulsions. Colloids Surf. A 1993, 71, 173–185. [Google Scholar] [CrossRef]
























| Class of Suspension Viscosity Model | Equation Numbers | References | Comments |
|---|---|---|---|
| Exact theoretical models | (2) | [2] | The exact theoretical models are based on single particle mechanics. The dipole strength of a single particle immersed in an infinite matrix fluid is calculated rigorously from the knowledge of flow fields around the particle. Using the dipole strength, the exact rheological constitutive equation for dilute suspension is developed. |
| Virial expansions of viscosity | (3) | [3,4,5,6,7] | Only the truncated form of the virial expansion of viscosity is useful as the virial coefficients of third and higher order are generally not known. |
| Effective medium models-no packing limit | (8), (12) | [11,12] | The drawback of these models is that they place no restriction on the amount of dispersed (particulate) phase that can be incorporated in a suspension. They allow the volume fraction of the dispersed particles to reach unity. This is physically impossible in a suspension of rigid particles. |
| Effective medium models—with packing limit | (14), (16), (26) | [13,14,23] | The effective medium models with packing limit are popular in the literature as they incorporate the effects of crowding and packing of particles on the suspension viscosity. The viscosity of suspension diverges when the packing limit is reached. However, the available models often fail to correctly account for the crowding and packing effects of particles on suspension viscosity. For example, the Mooney equation, Equation (14), often over predicts and the Krieger-Dougherty equation, Equation (16), often under predicts the suspension viscosity |
| Cell models | (17), (19), (20) | [15,16,17] | The drawback of the cell model approach is that it gives different expressions of suspension viscosity depending on the shape and size of the cell and the boundary condition specified at the boundary of the cell. There is no single equation (derived on the basis of the cell model approach) that is known to describe the viscosity data of suspensions adequately. |
| Models based on minimization of viscous energy dissipation | (24) | [21] | The Maron-Pierce-Quemada (MPQ) model, Equation (24), can be derived on the basis of minimization of viscous energy dissipation. One problem with the MPQ model is that it does not reduce to the exact theoretical model (Einstein equation) in the limit |
| Semi-empirical models | (21), (23), (25) | [18,19,22] | The drawback of these models is that they contain terms or factors which have no theoretical basis. Furthermore, there is no single semi-empirical equation that is known to describe the viscosity data of all suspensions. |
| Set No | Range of ϕ | Description | Source |
|---|---|---|---|
| 1 | 0–0.50 | Glass spheres, diameter range 100–160 µm | Vand [34] |
| 2 | 0–0.30 | Methyl methacrylate smooth spheres, non-Brownian particles, diameter ratio of largest to smallest particle 1.6:1 | Ward and Whitmore [35] |
| 3 | 0–0.30 | Methyl methacrylate smooth spheres, non-Brownian particles, diameter ratio of largest to smallest particle 3:1 | Ward and Whitmore [35] |
| 4 | 0–0.397 | Glass spheres, diameter range 5–10 µm | Lewis and Nielsen [36] |
| 5 | 0–0.410 | Glass spheres, diameter range 30–40 µm | Lewis and Nielsen [36] |
| 6 | 0–0.50 | Glass spheres, diameter range 45–60 µm | Lewis and Nielsen [36] |
| 7 | 0–0.45 | Glass spheres, diameter range 90–105 µm | Lewis and Nielsen [36] |
| 8 | 0–0.50 | Data represents average experimental viscosity curve drawn through several different suspension systems of non-Brownian spheres | Rutgers [37] |
| 9 | 0–0.57 | Data represents average experimental viscosity curve drawn through several different suspension systems of non-Brownian spheres | Thomas [19] |
| 10 | 0–0.512 | Glass spheres, diameter 230 µm | Ting and Luebbers [38] |
| 11 | 0–0.50 | Glass spheres, diameter 43 5.7 µm | Zarraga et al. [39] |
| 12 | 0–0.45 | Polystyrene spheres, 40 µm | Tanner et al. [40] |
| 13 | 0.50–0.576 | Monodispersed glass spheres, diameter ranging from 53.8 to 236 µm | Chong et al. [41] |
| 14 | 0–0.40 | Monodispersed solid spheres, suspensions of different diameter particles | Chong et al. [41] |
| 15 | 0–0.398 | Polystyrene spheres, diameter 700 µm | Ilic and Phan-Thien [42] |
| 16 | 0–0.50 | Monomodal suspensions, glass spheres average diameter 26 µm | Smith [43] |
| 17 | 0–0.50 | Monomodal suspensions, glass spheres average diameter 61 µm | Smith [43] |
| 18 | 0–0.5236 | Monomodal suspensions, glass spheres average diameter 125 µm | Smith [43] |
| 19 | 0–0.55 | Monomodal suspensions, glass spheres average diameter 183 µm | Smith [43] |
| 20 | 0–0.50 | Monomodal suspensions, glass spheres average diameter 221 µm | Smith [43] |
| Set No | Set No | ||
|---|---|---|---|
| 1 | 0.60 | 11 | 0.60 |
| 2 | 0.58 | 12 | 0.62 |
| 3 | 0.58 | 13 | 0.64 |
| 4 | 0.58 | 14 | 0.63 |
| 5 | 0.58 | 15 | 0.63 |
| 6 | 0.60 | 16 | 0.61 |
| 7 | 0.58 | 17 | 0.60 |
| 8 | 0.58 | 18 | 0.59 |
| 9 | 0.68 | 19 | 0.65 |
| 10 | 0.68 | 20 | 0.60 |
| Set No | Type of Emulsion | Range of ϕ | Viscosity Ratio (λ) | Description | Source |
|---|---|---|---|---|---|
| 1 | O/W | 0–0.60 | 4.15 × 10−3 | Polymer-thickened emulsions | Pal [51] |
| 2 | O/W | 0–0.60 | 1.12 × 10−2 | Polymer-thickened emulsions | Pal [51] |
| 3 | O/W | 0–0.60 | 5.82 × 10−2 | Polymer-thickened emulsions | Pal [52] |
| 4 | W/O | 0–0.65 | 1.65 × 10−1 | Mineral oil emulsions | Hsieh [53] |
| 5 | O/W | 0–0.596 | 2.574 | Mineral oil emulsions | Pal [54] |
| 6A | O/W | 0–0.516 | 5.52 | Set 6 emulsions prepared from same oil and aqueous phase but droplet sizes were different | Pal [55] |
| 6B | O/W | 0–0.494 | 5.52 | Pal [55] | |
| 6C | O/W | 0–0.553 | 5.52 | Pal [55] | |
| 6D | O/W | 0–0.543 | 5.52 | Pal [55] | |
| 7A | O/W | 0–0.343 | 5.573 | Milk-fat emulsions. The matrix phase consisted of skim milk, diluted, and concentrated skim milk | Leviton & Leighton [56] |
| 7B | O/W | 0–0.230 | 12.35 | Leviton & Leighton [56] | |
| 7C | O/W | 0–0.397 | 21.74 | Leviton & Leighton [56] | |
| 7D | O/W | 0–0.218 | 29.41 | Leviton & Leighton [56] | |
| 8 | O/W | 0–0.635 | 1.17 × 103 | Heavy oil emulsions | Pal [49] |
| 9 | O/W | 0–0.551 | 2.67 | Mineral oil emulsions | Pal [54] |
| 10 | O/W | 0–0.60 | 23.7 | Mineral oil emulsions | Bains [57] |
| 11 | O/W | 0–0.549 | 2.91 | Mineral oil emulsions | Buhidma [58] |
| 12 | O/W | 0–0.55 | 4.0 | Pickering type emulsions; droplets coated with a layer of solid nanoparticles | Wolf et al. [59] |
| 13 | O/W | 0.5 | 3.87 × 10−4–1.95 | Polymer-thickened emulsions | Pal [52,60] |
| 14 | O/W | 0.5 | 2.574–3.26 × 105 | Emulsions prepared from different viscosity oils | Pal [49,54,55,57,61] |
| 15 | O/W | 0.5 | 1.7–64.2 | Limpid and viscous paraffin emulsions | Sibree [62] |
| 16 | O/W | 0.5 | 0.834–123.1 | Emulsions prepared from three different oils: nujol, benzene, and olive oil | Broughton and Squires [63] |
| 17 | W/O | 0.5 | 0.153–0.447 | Emulsions prepared from different viscosity oils | Pal [54,64] |
| Set No | Set No | ||
|---|---|---|---|
| 1 | 0.637 | 7A–7D | 0.637 |
| 2 | 0.67 | 8 | 0.7404 |
| 3 | 0.7404 | 9 | 0.637 |
| 4 | 0.637 | 10 | 0.72 |
| 5 | 0.68 | 11 | 0.637 |
| 6A–6D | 0.66 | 12 | 0.637 |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pal, R. New Generalized Viscosity Model for Non-Colloidal Suspensions and Emulsions. Fluids 2020, 5, 150. https://doi.org/10.3390/fluids5030150
Pal R. New Generalized Viscosity Model for Non-Colloidal Suspensions and Emulsions. Fluids. 2020; 5(3):150. https://doi.org/10.3390/fluids5030150
Chicago/Turabian StylePal, Rajinder. 2020. "New Generalized Viscosity Model for Non-Colloidal Suspensions and Emulsions" Fluids 5, no. 3: 150. https://doi.org/10.3390/fluids5030150
APA StylePal, R. (2020). New Generalized Viscosity Model for Non-Colloidal Suspensions and Emulsions. Fluids, 5(3), 150. https://doi.org/10.3390/fluids5030150