Solving the fluid flow from the modified Navier–Stokes Equation (5) and the Fokker–Planck Equation (6) requires discretization and iteration on the two equations. It also requires the computation of the orientation tensors and , which have 21 unique components in total, in order to obtain the coupling of the equations. This needs to be executed through numerical integration in each computational cell and in each iteration. Shortly, solving the suspension flow comes with high computational cost. Solving the Fokker–Planck is also a complex problem itself. In the present work, a new model for the ODF is instead proposed. In addition, an implementation where explicit expressions for the orientation tensors as functions of the fluid flow are constructed prior to simulations is derived from the model with the use of Fourier series. The method substantially reduces the computational effort needed to solve the suspension flow, whilst keeping a lot of the detail in the anisotropic description of fibre stresses provided by the orientation distribution approach.
3.1. Modelling the ODF
In several numerical studies of the orientation distributions of fibres in turbulent suspension flows, slender fibres have been observed as tending to align with the fluid flow streamlines [
12,
14,
15,
16,
17]. Some of these results have also been confirmed with experimental data [
16,
17]. Lin [
16] also found that turbulent fluctuations have a randomizing effect on the alignment and that the alignment is faster the higher the aspect ratio of the fibres is. Therefore, the model developed in the present work was based on three main assumptions, namely;
Fibres are of high aspect ratio causing them to align according to the fluid flow direction with negligible delay;
The deviation of the alignment from the fluid flow direction increases with a magnitude of turbulent fluctuations; and
Fibres may be treated as rigid so that the Equations (4) and (5) may be used to described the stresses acted on the fluid by the suspended fibres.
The validity of the last assumption for softwood fibres may be discussed, as it leaves out possible degrees of freedom such as fibre bending, twisting and hooking, which causes contact forces affecting fibre suspension rheology [
4]. It was, though, assumed that the turbulence would cause these effects to be off small importance compared to the interaction between fibres and turbulent fluctuations, and that the orientation distribution approach itself was sufficient to describe the suspension rheology.
A statistical model is proposed were the ODF is explicitly determined by the local velocity direction and the turbulent intensity in the fluid flow. Using the model, the orientation tensors could in turn be computed for all possible cases and explicit expressions can be constructed for all orientation tensor components and , as functions of the flow field and prior to simulations. The explicit expressions may then be used to compute the fibre stress term in Equation (5) directly from the flow field. In this way, no additional differential equations need to be solved, and the numerical integration for the orientation tensors in each computational cell and iteration is also avoided. A large amount of computational effort is thus saved.
Fibre orientation is described using the angular components of a spherical coordinate system, which can be seen in
Figure 1, and the fibre orientation vector then reads [
12]:
The fibre orientation angles
and
are assumed to be independently normally distributed with means corresponding to the local velocity direction and with a common variance
as
where
and
are the angles corresponding to the local direction of fluid velocity. The probability density functions (pdf) of the distributions of
and
, respectively, then read (Rice, 2007) [
19]:
The modelled ODF, being the joint distribution of
and
, is then constructed as
ODF variance is connected to turbulence through the turbulent intensity of the flow. The randomizing effect on the fibre distribution caused by turbulent velocity fluctuations is modelled by letting the ODF standard deviation
be a linear function of the turbulent intensity
as
where
is the slope,
is a bulk velocity of the flow and
is the turbulent kinetic energy. A minimum value of
rad is defined considering perfect alignment being non-realistic. Since the expressions for the orientation tensors are to be constructed prior to simulations for a range of values of
, a limited interval is needed to be defined and thus a maximum for
needs to be defined. A maximum of
rad is defined being considered to cover the interval of realistic values observed in the literature [
12,
14,
15,
16,
17]. The construction of explicit expressions for the orientation tensors is described below.
3.2. Explicit a Priori Orientation Tensors
For a given ODF variance
and flow field direction
the modelled ODF is known and all orientation tensor components can be computed, as an example for
:
where the orientation vector components
consist of a product of functions of
and
, respectively, so that the tensor
can be written on the form
. The double integral can therefore be separated into two integrals and are then functions of the flow field angles
and
and are therefore denoted
and
, respectively. The values for
and
are computed through numerical integration for a series of discrete values for
and
, respectively, covering all possible fibre directions. The angles then cover the interval
, which may be interpreted from
Figure 1. Then, Fourier series expansions are applied and fitted to
and
, respectively, on the form Nordling and Österman, (2006) [
20]:
An expression for the tensor component is then constructed as
To allow for the ODF standard deviation to vary throughout the flow field, the procedure is repeated for a discrete series of values for
and the local value of
can then be computed by linear interpolation between the constructed expressions. The full procedure is applied to all orientation tensor components
and
. As a remark, only a number of terms up to
is needed to obtain a good fit for the Fourier series. An example can be seen for the component
in
Figure 2. A similarly good fit was obtained for all tensor components and for the range of values for the ODF standard deviation
used.
Using the model derived with the Fourier series implementation, the fibre stress term in Equation (5) can be computed directly from the flow field. The ODF does not need to be solved and the 21 unique components and do not need to be computed by numerical integration in each cell and iteration, as they are determined explicitly from the fluid flow. −
3.3. Model Implementation
In the present work, the model was intended for simulation with the commercial Computational Fluid Dynamics CFD software Ansys Fluent [
21]. The model described above was therefore implemented with the use of so-called user-defined functions (UDF), which are user-created subroutines to the built-in solver in Fluent written in the C programming language. In total, three UDFs were created and used to implement the ODF model for the Fluent framework. So-called user-defined scalar (UDS) variables, which are additional transport equations defined by the user, were used for the storage of variables and since Fluent automatically computes the gradient of all UDS variables. The solution of the UDS transport equation, however, was turned off. The first UDF computes the local values of orientation tensor components
and
from the explicit expressions constructed, described above. The six unique components of the fibre stress term
are then computed as
and stored in the six first UDS variable slots. The UDF then computes the three stress divergences terms
with the gradients of
obtained from the Fluent solver and stores them in the remaining three UDS variable slots. Three additional UDFs were then used to add the three terms as momentum sources in the respective momentum equations.
The expression for
, Equation (4), is rewritten to a function of fibre volume fraction
and fibre aspect ratio
. Using that, the volume concentration is the number of fibres per unit volume times the volume of a fibre:
an expression for
as a function of
and
reads:
so that Equation (4) may be written as
Since information on either
β and
or
and
may be missing in some cases, the model may contain uncertainties. It was therefore decided to introduce a constant, called
, to account for this. The constant
was introduced in the expression for additional viscosity due to fibres and Equation (24) was thus modifies as
3.5. Simulations
Simulations with the new ODF model was performed on the geometry (see
Figure 3), by applying a backward facing step method in order to validate the computed results through comparison with experimental data obtained by Claesson (2012) [
24] for softwood fibres.
The impact of changes in consistency or flow rate on flow structure after a backward facing step was investigated by comparing the reattachment length, at different fluid and flow properties. When the reattachment length was investigated, the point at the wall where the velocity changed from negative to positive was compared as Claesson (2012) [
24].
To minimise the introduction of modelling errors in addition to the ones from the fibre modelling, an accurate turbulence model was desired. The computational resources were, however, limited to a single laptop workstation with a four core Central Processing Unit CPU and direct numerical simulation (DNS) was therefore considered unfeasible. Wall-resolved large eddy simulation (LES) was also considered unaffordable as fine spatial and temporal resolution was needed in the near-wall region (Davidson, 2014) [
25]. Detached eddy simulations (DESs) were instead used, where the turbulent boundary layer was resolved by unsteady Reynolds-averaged Navier–Stokes equations RANS with the
Shear Stress Transport SST model and the outer region was resolved by LES (Davidson, 2014) [
25], as the model was considered sufficiently accurate.
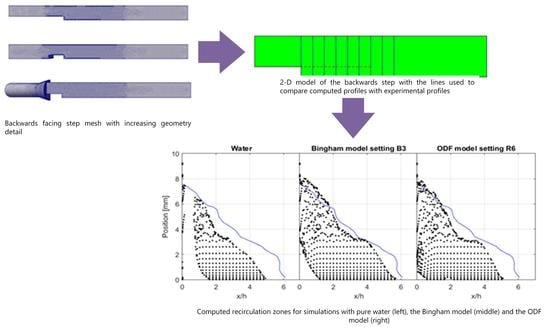
With the geometry resembling the experiments of Claesson (2012) [
24], a numerical mesh was generated accordingly. These simulations were conducted for pure water. The computed recirculation zone results were compared to the experiments. The level of detail of the mesh was then gradually increased and the procedure was repeated. A total number of three meshes were constructed and the final one was identified to be sufficient enough. The three meshes and the corresponding computed recirculation zones
, plotted with the experimental curves
from Claesson (2012) [
24] where
is the streamwise velocity, can be seen in
Figure 3. It can be observed that the changes in geometry have a clear impact on the computed results for the flow case in hand.
All meshes were generated with prism boundary layers and polyhedral cells of sizes suitable for DES. A symmetry boundary was used in the middle of the channel along the streamwise direction, which effectively reduced the number of elements by half. The final mesh consisted of approximately cells. A grid independence study was conducted on the mesh using simulations of pure water flow. A fine mesh with approximately cells and a coarse mesh with approximately cells was created. The study showed that the cell mesh had sufficient resolution to resolve the flow with the DES model.
Simulations with the ODF model were designed to match the conditions in Claesson (2012) [
24]. As data on experimental temperature conditions were not available, the simulations were carried out for water with viscosity
and density
, corresponding to a standard case with a temperature of 20 °C (Mörtstedt and Hellsten, 2010). Furthermore, the mass concentration
was used, and the aspect ratio
was used as a suitable value since softwood fibres have length of the millimetre scale and a diameter of a few microns [
6].
The mass concentrations for the different flow cases were given in Claesson (2012) [
24]. However, the unknown volume concentration
was needed to compute
. An approximation was therefore employed. A relation between volume concentration and mass concentration can be found in Derakhshandeh (2011) [
6], reading:
where
is the fibre density,
the amount of water absorbed in the fibre,
the volume of the hollow channel in the fibres per unit length and
the bulk density of the fibre suspension, which is approximately equal to the water density because of the low concentration. Now, since the main part of these quantities are unknown, it was assumed that they could be included in an overall approximation of the fibre density, such that:
Claesson (2012) [
24] used never-dried softwood pulp from a Swedish paper mill consisting of a mixture of fibres from pine and spruce. The values of dry densities of wood from pine and spruce are
and
, respectively [
26]. However, since the fibres were soaked by a significant amount of water, it was approximated that their water content was around 50%. The fibre density was calculated as the average of the wood’s dry density and the density of water, which is approximately equal to
. The fibre density was therefore approximated as the average of the dry density and the density of water as
Different parameter settings were used for simulations with the ODF model, both with the ODF standard deviation constant and varying linearly with turbulent intensity
. The constant
was also introduced, as shown in
Table 1, and was introduced in the expression for additional fibre viscosity
(Equation (24)). The aim was to investigate the sensitivity of changing the fibre stress term or, in extension, the sensitivity of modifying the fibre data, such as aspect ratio and volume concentration. The full set of parameter settings used for the ODF model is shown in
Table 1. A similar parameter study was performed for the Bingham model and the ideal setting was then used for comparison with the ODF model.
To avoid overfitting, due to only validating the fibre models with one experimental flow, the same were further validated by simulating a turbulent channel flow. Computed results were then compared to the experimental data from Xu and Aidun (2005) [
27] for softwood fibres. The turbulent flow was modelled with DES in the same way as for the backwards facing step case. The flow conditions and fibre data used were synchronized with the experimental conditions in Xu and Aidun (2005) [
27], where the fibre used in the experiments was natural flexible cellulous wood fibre with an average length of 2.3 mm and an average diameter of about 35 μm and the channel dimensions were 150 cm long, 5.08 cm wide and 1.65 cm high.
The simulations with the Bingham model over the backwards facing step were initialized by starting from stabilised transient simulations of pure water using DES with
SST turbulence model. The validation of the model was conducted in two separate steps. In the first step, three combinations of the parameters
a and
b were tested and chosen based on the results in Derakhshandeh et al. (2010) [
28], to identify the best combination compared to the experimental data. In the first step the constant µ
0 was kept with a same value as Ford et al. (2006) [
9]. In the second step of the validation, the effect on varying µ
0, by changing the same by a factor of approximately 2, were studied, combined along with the best combination of the parameters
a and
b and in the first step. In total, five parameter settings were used in the two steps, which are listed in
Table 2. The two validation steps are summarized in short below: