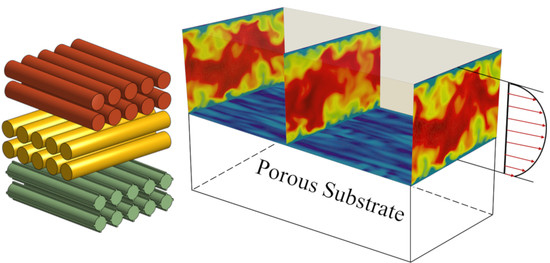
A Homogenization Approach for Turbulent Channel Flows over Porous Substrates: Formulation and Implementation of Effective Boundary Conditions

Abstract

The turbulent flow through a plane channel bounded by a single permeable wall is considered; this is a problem of interest since a carefully chosen distribution of grains and voids in the porous medium can result in skin friction reduction for the flow in the channel. In the homogenization approach followed here, the flow is not resolved in the porous layer, but an effective velocity boundary condition is developed (and later enforced) at a virtual interface between the porous bed and the channel flow. The condition is valid up to order two in terms of a small gauge factor, the ratio of microscopic to macroscopic length scales; it contains slip coefficients, plus surface and bulk permeability coefficients, which arise from the solution of microscale problems solved in a representative elementary volume. Using the effective boundary conditions, free of empirical parameters, direct numerical simulations are then performed in the channel, considering a few different porous substrates. The results, examined in terms of mean values and turbulence statistics, demonstrate the drag-reducing effects of porous substrates with streamwise-preferential alignment of the solid grains.

1. Introduction

The large skin-friction drag characterizing wall-bounded turbulent flows, as compared to laminar ones, represents a major challenge in engineering applications where efficiency and running costs of fluid transport systems are of interest. This has motivated several experimental and numerical studies aimed at a better understanding of the phenomenon of turbulence production and generation of Reynolds shear stress in such flows [1,2,3,4]; the coherent structures in the inner region of the wall layer and the bursting (ejection) and sweep (inrush) events related to such structures have been the object of intense research activities [5,6,7,8]. The design of active or passive techniques for turbulent drag reduction requires in-depth understanding of the interacting mechanisms which contribute to near-wall turbulence, in order for its effective control. The near-wall flow is characterized by a self-sustaining cycle responsible for the regeneration of turbulent fluctuations, owing to the dynamic interaction between longitudinal velocity streaks and quasi-streamwise vortices; this cycle is independent of the nature of the outer flow [9]. Attenuating (or suppressing) any of the processes involved in this autonomous cycle can lead to a less disturbed flow field (or even to relaminarization) [9], a clear advantage when the objective of the control is skin-friction drag.

Many investigations have been conducted to optimize and assess the effectiveness and feasibility of active and passive drag reduction techniques, to favorably alter the structure of the turbulent boundary layer. Active techniques, involving energy input, have proved to yield significant drag reduction in wall-bounded turbulent flows. For instance, optimized uniform blowing of the fluid through a spanwise slot can produce a local drag reduction of $80\%$ downstream of the slot [10], while sufficiently high suction rates through a short porous flush-mounted strip can allow for local relaminarization of the turbulent boundary layer, resulting in a drag reduction of more than $50\%$ [11]. Counter-rotating large-scale streamwise vortices, externally initiated by a transverse array of longitudinal plasma actuators, can stabilize the streaks in the near-wall flow and attenuate the coherent structures, interrupting the turbulence regeneration cycle; a drag reduction of more than $25\%$ can be achieved [12,13]. Other studies focused on forcing wall-normal fluctuations [14] or in-plane wall oscillations [15,16]. Passive drag reduction techniques have also been investigated extensively, along with remarkable advances in bio-inspired designs. Riblets (longitudinal surface grooves) have proved to mitigate the velocity fluctuations near the wall, resulting in a more uniform flow field [17]; studies on different configurations of riblets revealed that an optimized drag reduction of almost $10\%$ can be achieved [18]. Super-hydrophobic surfaces can reduce drag up to approximately $80\%$ under optimal conditions, mainly due to the large effective slip of aqueous solutions on the walls [19]. The ability of anisotropic permeable substrates to reduce skin-friction drag in turbulent channel flows has recently attracted much interest; this constitutes the main objective of the present study.

Porous substrates are encountered in various natural and engineering applications, and have been a source of inspiration for many studies in which the influence of wall permeability has been assessed on the behavior of the overlying turbulent boundary layer and ensuing drag alteration. Several configurations of the porous substrate have been investigated, with different values of the porosity ($\theta$) and at different flow conditions. The main parameters tested in previous studies are the diagonal components of the permeability tensor of the porous medium (${\mathcal{K}}_{xx}$, ${\mathcal{K}}_{yy}$, ${\mathcal{K}}_{zz}$) and the Navier-slip coefficients (${\lambda }_x$, ${\lambda }_z$) at the dividing surface between the free-fluid region in the channel and the permeable layer. In the following, x, y and z denote, respectively, the streamwise, wall-normal and spanwise directions. The numerical work by Rosti et al. [20] on turbulent channel flows over isotropic porous substrates (${\mathcal{K}}_{xx}={\mathcal{K}}_{yy}={\mathcal{K}}_{zz}$) has shown that even small values of the medium permeability can affect the response of the adjacent turbulent boundary layer: the disturbances were found to be intensified and the Reynolds stresses enhanced, with a consequent increase in skin-friction drag. This is in general agreement with the findings of earlier studies [21,22,23]. A similar behavior of disturbance intensification is observed when the porous substrates have preferential spanwise permeability. Wang et al. [24] investigated the dynamic interaction between a turbulent channel flow and a porous bed made of spanwise-aligned cylinders, for which ${\mathcal{K}}_{zz}>{\mathcal{K}}_{xx}={\mathcal{K}}_{yy}$. The structure of the blowing (upwelling) and suction (downwelling) events through the pores has been analyzed, particularly in terms of their role on the onset of the Kelvin–Helmholtz instability near the permeable wall. Other studies have focused on permeable walls potentially capable to yield turbulent drag reduction. Rosti et al. [25] studied the turbulent flow over anisotropic porous beds characterized by equal values of the permeability in the streamwise and the spanwise directions, i.e., ${\mathcal{K}}_{xx}={\mathcal{K}}_{zz}\ne {\mathcal{K}}_{yy}$. They showed that a drag reduction of up to 20% can be achieved from walls of high in-plane permeability (${\mathcal{K}}_{xx}={\mathcal{K}}_{zz}>>{\mathcal{K}}_{yy}$), whereas the skin-friction drag may increase by the same amount for substrates of preferential wall-normal permeability. Among the different configurations considered in the literature, the use of porous substrates of preferential permeability along the streamwise direction, consisting, e.g., of longitudinal cylinders with ${\mathcal{K}}_{xx}>>{\mathcal{K}}_{zz}={\mathcal{K}}_{yy}$, appears to provide the best results in terms of turbulent drag reduction. The drag reduction curves for this configuration are similar to those of riblets [26], and the theory behind the ability of such substrates to reduce skin-friction drag has been elaborated by Abderrahaman-Elena and García-Mayoral [27]. Conceptually, the drag reduction ($DR$) is proportional to the difference between the slip lengths along the streamwise and the spanwise directions, that is, $DR\approx {\mu }_0({\lambda }_x^{+}-{\lambda }_z^{+})$ [28,29], which has been approximated by ${\mu }_0\xi \left(\sqrt{{\mathcal{K}}_{xx}^{+}}-\sqrt{{\mathcal{K}}_{zz}^{+}}\right)$ [27]. All the macroscopic parameters are measured in wall units and this is indicated by the superscript ‘+’; the coefficient ${\mu }_0$ is a function of the Reynolds number [30], while the parameter $\xi$ characterizes the inter-connectivity of the flow between the pores [27]. The relation above in terms of the square root of the permeability components holds for substrates of relatively low wall-normal permeability; if ${\mathcal{K}}_{yy}^{+}$ exceeds some critical threshold, Kelvin–Helmholtz-like rollers are developed near the interface, and the drag reduction mechanism is adversely affected [31].

With the significant progress in manufacturing and fabrication techniques, the study of the interaction between the microscale features of the surface (such as roughness, porosity, irregularity, compliance, etc.) and the adjacent fluid flow has become more important for several applications. The numerical complexity of fully resolving the micro-details of the surface in Direct Numerical Simulations (DNS) or even in Large Eddy Simulations (LES) of turbulence represents a challenge, especially if optimization of the surface is the ultimate goal. The multiscale homogenization approach adopted in this paper is a mathematical framework through which the rapidly varying properties of the surface (the porous substrate in the present case) can be replaced by upscaled properties such as slip, interface permeability, etc. [32,33], which contribute to the definition of effective boundary conditions at a virtual plane surface. The macroscale behavior of, for instance, the turbulent channel flow is then targeted, bypassing the need to fully resolve the motion within the permeable substrate; the mesh requirements of the numerical simulations are therefore significantly alleviated. Multiscale homogenization has been known and used by applied mathematicians for a long time. In more recent years, it has been rediscovered and applied to a variety of physically relevant cases. Although the classical first-order slip condition over a generic solid surface, proposed by Navier [34], was based on empirical considerations concerning the near-wall flow behavior, recent studies adopting the homogenization technique have provided a robust mathematical framework for the estimation of Navier’s slip length, $\lambda$, without the need for any ad hoc correlation [35]. A tensorial generalization of the first-order Navier’s slip condition over a micro-textured surface was given by Zampogna et al. [36], via the definition of a third-order slip tensor which depends on the geometry of the roughness pattern. The homogenized model was later extended to study the fluid motion over deformable riblets, to assess the potential drag reduction [37]. The so-called transpiration-resistance model by Lācis et al. [38] shed light on the role of the wall-normal velocity at the fictitious interface in improving the predictions of the homogenization-based direct simulations for turbulent flows over micro-patterned surfaces. The homogenization model for the flow over a rough surface was later pushed to third-order in terms of a small parameter, ratio of microscopic to macroscopic length scales, by Bottaro and Naqvi [39]. Most recently, the asymptotic homogenization theory has been employed by Ahmed et al. [40] to study buoyancy-driven flows over vertical rough surfaces, by deriving and implementing upscaled velocity and temperature boundary conditions at a smooth virtual surface. Effective boundary conditions at the interface between a porous bed and an unconfined flow region have been explored by Sudhakar et al. [41] and by Naqvi and Bottaro [42].

In this work, asymptotic homogenization is used to derive second-order accurate effective boundary conditions for the three velocity components at a fictitious interface, chosen tangent to the porous material, to macroscopically mimic the effects of the small-scale features of an anisotropic porous layer on a turbulent boundary layer. The technique relies on reconstructing the microscale problem via asymptotic expansions of the microscopic dependent variables (velocity components and pressure) in powers of a small parameter $ϵ$, which represents the ratio between two well-separated scales, for instance the periodicity of the porous pattern (microscopic length scale) and half the channel height (macroscopic length scale). The problem is then solved up to any order in $ϵ$ via numerical solution of ad hoc auxiliary systems which hold in a doubly periodic representative elementary volume. The equations governing the physical problem, the domain decomposition, and the chosen scales for each sub-domain are outlined in Section 2, with detailed explanation of the adopted asymptotic approach and with illustration of the numerical solutions for the auxiliary problems that arise. Different configurations of the porous substrate are considered for the evaluation of the macroscopic coefficients of the model, in particular, spanwise- and streamwise-aligned elements of two different shapes.The macroscopic problem is addressed in Section 3. A direct numerical simulation was first conducted for a turbulent flow through a channel with smooth, impermeable walls at $R{e}_{\tau }\approx 190$, to validate the numerical code, the domain size, etc. The wall-bounded turbulent flow over a porous substrate is then considered. Standard turbulence statistics are compared for different porous substrates, and consequent skin-friction drag increase/reduction is indicated. The main findings of the study are highlighted in the concluding section.

2. The Homogenization Model

This section is dedicated to providing the details to derive effective boundary conditions at the fictitious interface between a channel flow and a porous substrate underneath. The procedure represents an extension of the model by Naqvi and Bottaro [42], in which only isotropic or two-dimensional porous media were analyzed; in the present work, a three-dimensional, transversely isotropic, permeable bed is considered.

2.1. Governing Equations and Domain Decomposition

Let us consider, for instance, a porous substrate made of regularly arranged, streamwise-aligned solid inclusions with given periodicity in the spanwise and wall-normal directions, cf. Figure 1. It is possible to identify two characteristic length scales, a microscopic one related to the porous medium, l (the periodicity of the configuration), and a macroscopic one related to the large-scale motion in the channel, H (half the channel thickness). The mass and momentum conservation equations governing the flow of a viscous, incompressible, Newtonian fluid can be expressed in terms of the dimensional variables $\widehat{•}$ as follows:

$$\frac{\partial {\widehat{u}}_i}{\partial {\widehat{x}}_i}=0,\rho \left(\frac{\partial {\widehat{u}}_i}{\partial \widehat{t}}+{\widehat{u}}_j\frac{\partial {\widehat{u}}_i}{\partial {\widehat{x}}_j}\right)=-\frac{\partial \widehat{p}}{\partial {\widehat{x}}_i}+\mu \frac{{\partial }^2{\widehat{u}}_i}{\partial {\widehat{x}}_j^2},$$

(1)

with $\rho$ the fluid density, $\mu$ the dynamic viscosity, $\widehat{p}$ the pressure, ${\widehat{u}}_i$ the velocity components (${\widehat{u}}_1=\widehat{u}$, ${\widehat{u}}_2=\widehat{v}$, ${\widehat{u}}_3=\widehat{w}$), ${\widehat{x}}_i$ the space coordinates (${\widehat{x}}_1=\widehat{x}$, ${\widehat{x}}_2=\widehat{y}$, ${\widehat{x}}_3=\widehat{z}$), and $\widehat{t}$ time. The streamwise direction (${\widehat{x}}_1$), the wall-normal direction (${\widehat{x}}_2$), and the spanwise direction (${\widehat{x}}_3$) are indicated in Figure 1.

Provided that $l\ll H$, the microscopic problem is amenable to a multiple-scale expansion in terms of a small parameter $ϵ=l/H\ll 1$. The full domain is decomposed into three sub-domains: a channel-flow region away from the interface (superscript “$\mathcal{C}$”), an interface region (superscript “$\mathcal{I}$”) and a region within the porous layer away from boundaries, governed by Darcy’s law (superscript “$\mathcal{P}$”). The normalized variables in the three regions are introduced as follows:

Channel-flow region ${}^{\mathcal{C}}$:

$$X_i={\widehat{x}}_i/H,P^{\mathcal{C}}=\widehat{p}/\left(\rho {\mathcal{U}}^2\right),U_i^{\mathcal{C}}=\widehat{u}/\mathcal{U}.$$

(2)

Interface region ${}^{\mathcal{I}}$:

$$x_i={\widehat{x}}_i/\ell ,P^{\mathcal{I}}=\widehat{p}/(\mu \mathcal{U}/H),U_i^{\mathcal{I}}={ϵ}^{-1}\widehat{u}/\mathcal{U}.$$

(3)

Porous region ${}^{\mathcal{P}}$:

$$x_i={\widehat{x}}_i/\ell ,P^{\mathcal{P}}=\widehat{p}/(\mu \mathcal{U}/H),U_i^{\mathcal{P}}={ϵ}^{-2}\widehat{u}/\mathcal{U},$$

(4)

with $\mathcal{U}$ a suitable macroscopic velocity scale, for instance the bulk velocity in $0\le \widehat{y}\le 2H$. The normalization above leads to the following dimensionless systems in the ${•}^{\mathcal{C}}$, ${•}^{\mathcal{I}}$, and ${•}^{\mathcal{P}}$ regions, respectively;

$$\frac{\partial U_i^{\mathcal{C}}}{\partial X_i}=0,\frac{\partial U_i^{\mathcal{C}}}{\partial t}+U_j^{\mathcal{C}}\frac{\partial U_i^{\mathcal{C}}}{\partial X_j}=-\frac{\partial P^{\mathcal{C}}}{\partial X_i}+\frac{1}{Re}\frac{{\partial }^2{U}_i^{\mathcal{C}}}{\partial X_j^2},$$

(5)

$$\frac{\partial U_i^{\mathcal{I}}}{\partial x_i}=0,{ϵ}^{2}Re\left(\frac{\partial U_i^{\mathcal{I}}}{\partial t}+U_j^{\mathcal{I}}\frac{\partial U_i^{\mathcal{I}}}{\partial x_j}\right)=-\frac{\partial P^{\mathcal{I}}}{\partial x_i}+\frac{{\partial }^2{U}_i^{\mathcal{I}}}{\partial x_j^2},$$

(6)

$$ϵ\frac{\partial U_i^{\mathcal{P}}}{\partial x_i}=0,{ϵ}^{4}Re{U}_j^{\mathcal{P}}\frac{\partial U_i^{\mathcal{P}}}{\partial x_j}=-\frac{\partial P^{\mathcal{P}}}{\partial x_i}+ϵ\frac{{\partial }^2{U}_i^{\mathcal{P}}}{\partial x_j^2},$$

(7)

with ${\displaystyle Re=\frac{\rho \mathcal{U}H}{\mu }}$. In the channel-flow region, the dependent variables are function of the macroscopic coordinates $X_i$ only, whereas, in the intermediate and porous regions, the dependent variables depend on both microscopic and macroscopic coordinates ($x_i$, $X_i$ respectively). The continuity of the fields across the interface between the ${•}^{\mathcal{C}}$ and ${•}^{\mathcal{I}}$ regions is represented by matching the velocity and the traction vectors at a dividing surface. If $x_2=y=y_{\infty }$ is taken to be the microscopic vertical coordinate of this interface, and $Y=\mathcal{Y}=ϵy_{\infty }$ is the macroscopic vertical position at which the effective conditions are enforced, the matching conditions may be written as follows:

$$\underset{y\to y_{\infty }}{lim}{U}_i^{\mathcal{I}}=\frac{1}{ϵ}\underset{Y\to \mathcal{Y}}{lim}{U}_i^{\mathcal{C}},$$

(8)

$${\displaystyle \underset{y\to y_{\infty }}{lim}-P^{\mathcal{I}}{\delta }_{i2}+\frac{\partial V^{\mathcal{I}}}{\partial x_i}+\frac{\partial U_i^{\mathcal{I}}}{\partial y}=\underset{Y\to \mathcal{Y}}{lim}-Re{P}^{\mathcal{C}}{\delta }_{i2}+\frac{\partial V^{\mathcal{C}}}{\partial X_i}+\frac{\partial U_i^{\mathcal{C}}}{\partial Y},}$$

(9)

with ${\delta }_{ij}$ the Kronecker index. The conditions above are acceptable provided $y_{\infty }$ is sufficiently large for the ${•}^{\mathcal{I}}$ variables to become independent of x and z there. Should this not be the case, integration of the interface variables along the x and z direction must be performed before matching velocity and traction components.

2.2. Asymptotic Analysis of the Microscale Problem

The velocity and pressure fields in porous and interface regions are asymptotically expanded in terms of $ϵ$, for instance $U_i^I=u_i^{\left(0\right)}+ϵu_i^{\left(1\right)}+{ϵ}^2{u}_i^{\left(2\right)}+\cdots$, and the gradients are recast based on the chain rule (${\displaystyle \frac{\partial }{\partial x_i}\to \frac{\partial }{\partial x_i}+ϵ\frac{\partial }{\partial X_i}}$). The asymptotic expressions are plugged into the microscale governing equations and read:

$$\left\{\begin{array}{c}{\partial }_i{u}_i=-ϵ{\partial }_i^{\prime }{u}_i^{\left(0\right)}+\mathcal{O}\left({ϵ}^2\right),\hfill \\ -{\partial }_{i}p+{\partial }_j^2{u}_i=ϵ\left[{\partial }_i^{\prime }{p}^{\left(0\right)}-2{\partial }_j{\partial }_j^{\prime }{u}_i^{\left(0\right)}\right]+\mathcal{O}\left({ϵ}^2\right),\hfill \end{array}\right.$$

(10)

with the microscopic and macroscopic derivatives indicated, respectively, by

$${\partial }_i=\frac{\partial }{\partial x_i},{\partial }_i^{\prime }=\frac{\partial }{\partial X_i}.$$

The microscale problem can be reconstructed at different orders of $ϵ$. The leading-order problem reads:

$$\mathcal{O}\left(1\right):\left\{\begin{array}{c}{\partial }_i{u}_i^{\left(0\right)}=0,\hfill \\ -{\partial }_i{p}^{\left(0\right)}+{\partial }_j^2{u}_i{}^{\left(0\right)}=0,\hfill \\ {\left.-p^{\left(0\right)}{\delta }_{i_2}+{\partial }_2{u}_i^{\left(0\right)}+{\partial }_i{u}_2^{\left(0\right)}\right|}_{y_{\infty }}=S_{i2}^{\mathcal{C}}.\hfill \end{array}\right.$$

(11)

At the next order we obtain:

$$\mathcal{O}\left(ϵ\right):\left\{\begin{array}{c}{\partial }_i{u}_i^{\left(1\right)}=-{\partial }_i^{\prime }{u}_i^{\left(0\right)},\hfill \\ -{\partial }_i{p}^{\left(1\right)}+{\partial }_j^2{u}_i^{\left(1\right)}={\partial }_i^{\prime }{p}^{\left(0\right)}-2{\partial }_j{\partial }_j^{\prime }{u}_i^{\left(0\right)},\hfill \\ {\left.-p^{\left(1\right)}{\delta }_{i_2}+{\partial }_2{u}_i^{\left(1\right)}+{\partial }_i{u}_2^{\left(1\right)}\right|}_{y_{\infty }}=-{\left.{\partial }_2^{\prime }{u}_i^{\left(0\right)}+{\partial }_i^{\prime }{u}_2^{\left(0\right)}\right|}_{y_{\infty }},\hfill \end{array}\right.$$

(12)

where $S_{i2}^{\mathcal{C}}$ is the macroscopic traction vector evaluated at $Y=\mathcal{Y}$, i.e.,

$$S_{i2}^{\mathcal{C}}={\sigma }^{\mathcal{C}}·{\mathit{e}}_2{|}_{Y=\mathcal{Y}}={\left.\left(\frac{\partial U^{\mathcal{C}}}{\partial Y}+\frac{\partial V^{\mathcal{C}}}{\partial X},-Re{P}^{\mathcal{C}}+2\frac{\partial V^{\mathcal{C}}}{\partial Y},\frac{\partial W^{\mathcal{C}}}{\partial Y}+\frac{\partial V^{\mathcal{C}}}{\partial Z}\right)\right|}_{Y=\mathcal{Y}},$$

(13)

with ${\sigma }^{\mathcal{C}}$ as the stress tensor. From now on, the superscript ${•}^{\mathcal{C}}$ is omitted when referring to outer flow dependent variables.

Owing to the linearity of Equations (11) and (12), generic forms of the solutions can be assumed. For the leading-order problem, the dependent variables can be expressed as

$$\left\{\begin{array}{c}{u}_i^{\left(0\right)}=u_{ij}^{†}{S}_{j2},\hfill \\ p^{\left(0\right)}=p_j^{†}{S}_{j2},\hfill \end{array}\right.$$

(14)

with the new parameters, $u_{ij}^{†}$ and $p_j^{†}$ functions of only $x_i$. Three decoupled systems of equations, the so-called auxiliary problems, arise from substituting the preceding expressions into Equation (11); they can be summarized as follows:

$$\left\{\begin{array}{c}{\partial }_i{u}_{ij}^{†}=0,\hfill \\ -{\partial }_i{p}_j^{†}+{\partial }_l^2{u}_{ij}^{†}=0,\hfill \\ {\left.\left(-p_j^{†}{\delta }_{i2}+{\partial }_2{u}_{ij}^{†}+{\partial }_i{u}_{2j}^{†}\right)\right|}_{y_{\infty }}={\delta }_{ij},\hfill \end{array}\right.$$

(15)

where the three microscopic problems corresponds to $j=1,2,3$. For $j=2$, one finds the simple analytical solution:

$$u_{i2}^{†}=0,p_2^{†}=-1.$$

These results will directly enter, and simplify, the $\mathcal{O}\left(ϵ\right)$ problems.

At $\mathcal{O}\left(ϵ\right)$, the following generic forms hold:

$$\left\{\begin{array}{c}{u}_i^{\left(1\right)}=u_{ijk}^{‡}{\partial }_k^{\prime }{S}_{j2},\hfill \\ p^{\left(1\right)}=p_{jk}^{‡}{\partial }_k^{\prime }{S}_{j2}.\hfill \end{array}\right.$$

(16)

This leads to

$$\left\{\begin{array}{c}-{\partial }_i{\partial }_i{u}_{ijk}^{‡}=-u_{kj}^{†},\hfill \\ p_{jk}^{‡}-p_j^{†}{\delta }_{ki}+{\partial }_l^2{u}_{ijk}^{‡}+2{\partial }_k{u}_{ij}^{†}=0,\hfill \\ {\left.\left(-p_{jk}^{‡}{\delta }_{i2}+{\partial }_2{u}_{ijk}^{‡}+{\partial }_i{u}_{2jk}^{‡}\right)\right|}_{y_{\infty }}=-{\left.\left(u_{ij}^{†}{\delta }_{k2}+u_{2j}^{†}{\delta }_{ik}\right)\right|}_{y_{\infty }},\hfill \end{array}\right.$$

(17)

which are nine decoupled problems to be solved in the microscopic cell, for $j,k=1,2,3$. All these problems are subject to periodicity along x and z (for streamwise-aligned solid inclusions) and to the no-slip condition on the solid grains of the porous medium.

Numerical results are sought, in particular, at $y=y_{\infty }$, since ${\left.u_{ij}^{†}\right|}_{y_{\infty }}$ and ${\left.u_{ijk}^{‡}\right|}_{y_{\infty }}$ are eventually the numerical coefficients needed to close the macroscopic effective conditions. These conditions arise from matching the velocity vector at the specified interface (cf. Equation (8)); finally, the second-order accurate upscaled conditions at the dividing surface are:

$${\left.U_i\right|}_{Y=ϵy_{\infty }}=ϵ\left({\left.u_i^{\left(0\right)}\right|}_{y_{\infty }}+ϵ{\left.u_i^{\left(1\right)}\right|}_{y_{\infty }}\right)+\mathcal{O}\left({ϵ}^3\right)=ϵ{\left.{\tilde{u}}_{ij}\right|}_{y_{\infty }}{S}_{j2}+{ϵ}^2{\left.u_{ijk}^{‡}\right|}_{y_{\infty }}\frac{\partial S_{j2}}{\partial X_k}+\mathcal{O}\left({ϵ}^3\right).$$

(18)

2.3. Numerical Solutions of the Auxiliary Systems

With the aid of the Comsol Multiphysics^® software (version 5.2, COMSOL Inc, Stockholm, Sweden), the auxiliary systems formulated in Section 2.2 are solved on a microscopic elongated domain, considering streamwise-aligned cylindrical inclusions. Specifically, the domain consists of a $xyz$ box of sides $[1,2y_{\infty },1]$; cf. Figure 2. The value of $y_{\infty }$ is specified such that the microscopic fields are homogeneous in x and z near $y=y_{\infty }$. It was numerically confirmed that $y_{\infty }=5$ is sufficient to satisfy the preceding condition. The dividing surface is set at $y=0$, the surface tangent to the uppermost cylinder, so that half of the domain ($0<y\le y_{\infty }$) is above it and the other half ($-y_{\infty }\le y<0$) is below it. For $-y_{\infty }\le y<0$, identical longitudinal cylinders are present, regularly spaced of one unit of length along y. The diameter of the cylinders was changed to study the effects of varying the porosity of the substrate, defined as $\theta ={\mathcal{V}}_{fluid}/{\mathcal{V}}_{tot}$, with ${\mathcal{V}}_{fluid}$ and ${\mathcal{V}}_{tot}$ the fluid’s volume in a cubic unit cell within the porous domain and the total volume of the unit cell, respectively.

The numerical solutions of the auxiliary sub-systems related to the $\mathcal{O}\left(1\right)$ problem, i.e., Equation (15), reveal that $u_{11}^{†}$ and $u_{33}^{†}$ are the only variables which do not vanish at the matching surface ($y=y_{\infty }=5$). The contours of the two parameters throughout the microscopic domain are displayed in Figure 2; for brevity, fields of the other variables are not presented. Subsequently, the effect of varying the location of the matching interface was considered, by gradually increasing the value of $y_{\infty }$ and monitoring the behaviors of $u_{11}^{†}$ and $u_{33}^{†}$. Linear trends have been detected, in the same manner as for the case of the fluid motion over a rough surface [39], i.e.,

$${\left.u_{11}^{†}\right|}_{y_{\infty }}=y_{\infty }+{\lambda }_x,{\left.u_{33}^{†}\right|}_{y_{\infty }}=y_{\infty }+{\lambda }_z,$$

(19)

with ${\lambda }_x$ and ${\lambda }_z$ the dimensionless Navier-slip coefficients in the streamwise and the spanwise directions, respectively.

Solutions of the higher-order systems were then sought. The following trends of the microscopic parameters, with non-zero magnitudes at the matching interface, are obtained (the reader is referred to [39,42] for more details about the procedure):

$$\begin{array}{c}-{\left.u_{211}^{‡}\right|}_{y_{\infty }}={\left.u_{121}^{‡}\right|}_{y_{\infty }}=0.5y_{\infty }^2+{\lambda }_x{y}_{\infty }+{\mathcal{K}}_{xy}^{itf},\hfill \\ -{\left.u_{233}^{‡}\right|}_{y_{\infty }}={\left.u_{323}^{‡}\right|}_{y_{\infty }}=0.5y_{\infty }^2+{\lambda }_z{y}_{\infty }+{\mathcal{K}}_{zy}^{itf},\hfill \\ {\left.u_{222}^{‡}\right|}_{y_{\infty }}={\mathcal{K}}_{yy},\hfill \end{array}$$

(20)

where ${\mathcal{K}}_{yy}$ is a medium permeability component, while ${\mathcal{K}}_{xy}^{itf}$ and ${\mathcal{K}}_{zy}^{itf}$ are interface permeabilities.

At this point, it is advantageous to extrapolate the solutions of the parameters of interest to a matching interface located at $y=0$. This can be achieved simply by setting $y_{\infty }=0$ in the fitting relations (Equations (19) and (20)). Thus, the values of the coefficients ${\lambda }_x,{\lambda }_z,{\mathcal{K}}_{xy}^{itf},{\mathcal{K}}_{zy}^{itf}$ and ${\mathcal{K}}_{yy}$ are sufficient to describe the presence of the permeable interface up to the second order in terms of $ϵ$, by enforcing effective boundary conditions on the plane $y=0$. These coefficients characterize the microstructure of the porous substrate; for instance, they are dependent on the shape of the inclusions, their orientation and the porosity $\theta$.

Simple methods can also be adopted to calculate the coefficients of interest, based on previous findings [39,42]. The Navier-slip coefficients (${\lambda }_x,{\lambda }_z$) can be computed by averaging the fields of $u_{11}^{†}$ and $u_{33}^{†}$ (those shown in Figure 2), respectively, over the plane $y=0$. The numerical values of ${\mathcal{K}}_{xy}^{itf}$ and ${\mathcal{K}}_{zy}^{itf}$ can be recovered by taking the following volume integrals:

$$\begin{array}{c}{\mathcal{K}}_{xy}^{itf}={\int }_{{\mathcal{V}}_{f_{Por}}}{u}_{11}^{†}\mathrm{d}V,\hfill \\ {\mathcal{K}}_{zy}^{itf}={\int }_{{\mathcal{V}}_{f_{Por}}}{u}_{33}^{†}\mathrm{d}V,\hfill \end{array}$$

(21)

where ${\mathcal{V}}_{f_{Por}}$ denotes the whole fluid volume in the elementary cell below the interface. This method is particularly convenient since it means that interface permeabilities are already available from the $\mathcal{O}\left(1\right)$ problems, i.e., there is no need to solve the $\mathcal{O}\left(ϵ\right)$ ones to compute them. Finally, as far as ${\mathcal{K}}_{yy}$ is concerned, one can compute it by simulating the $\mathcal{O}\left(ϵ\right)$ system governing $u_{222}^{‡}$ in a fully periodic unit cell (cf. Figure 3) and evaluating the integral:

$${\mathcal{K}}_{yy}={\int }_{{\mathcal{V}}_{fluid}}{u}_{222}^{‡}\mathrm{d}V.$$

(22)

Should they be needed, the other diagonal components of the medium permeability tensor can be retrieved in the following way:

$$\begin{array}{c}{\mathcal{K}}_{xx}={\int }_{{\mathcal{V}}_{fluid}}{u}_{121}^{‡}\mathrm{d}V,\hfill \\ {\mathcal{K}}_{zz}={\int }_{{\mathcal{V}}_{fluid}}{u}_{323}^{‡}\mathrm{d}V.\hfill \end{array}$$

(23)

We remark that, in this case, ${\mathcal{K}}_{xx}$ and ${\mathcal{K}}_{zz}$ do not correspond to any value of ${\left.u_{ijk}^{‡}\right|}_{y_{\infty }=0}$, and do not contribute to the interface conditions. Eventually, the following values of the macroscopic coefficients were attained for the case of longitudinal cylindrical inclusions with porosity $\theta =0.5$:

$$\begin{array}{c}{\lambda }_x=0.06883,{\lambda }_z=0.04513,{\mathcal{K}}_{xy}^{itf}=0.005561,{\mathcal{K}}_{zy}^{itf}=0.002220,\\ {\mathcal{K}}_{xx}=0.006966,{\mathcal{K}}_{yy}=0.001828,{\mathcal{K}}_{zz}=0.001828.\end{array}$$

(24)

2.4. Formal Expressions of the Effective Boundary Conditions

The effective boundary conditions are

$${\left.U\right|}_{Y=0}={\left.ϵ{\lambda }_x{S}_{12}\right|}_{Y=0}+{\left.{ϵ}^2{\mathcal{K}}_{xy}^{itf}\frac{\partial S_{22}}{\partial X}\right|}_{Y=0}+\mathcal{O}\left({ϵ}^3\right),$$

(25)

$${\left.V\right|}_{Y=0}=-{\left.{ϵ}^2{\mathcal{K}}_{xy}^{itf}\frac{\partial S_{12}}{\partial X}\right|}_{Y=0}-{\left.{ϵ}^2{\mathcal{K}}_{zy}^{itf}\frac{\partial S_{32}}{\partial Z}\right|}_{Y=0}+{\left.{ϵ}^2{\mathcal{K}}_{yy}\frac{\partial S_{22}}{\partial Y}\right|}_{Y=0}+\mathcal{O}\left({ϵ}^3\right),$$

(26)

$${\left.W\right|}_{Y=0}={\left.ϵ{\lambda }_z{S}_{32}\right|}_{Y=0}+{\left.{ϵ}^2{\mathcal{K}}_{zy}^{itf}\frac{\partial S_{22}}{\partial Z}\right|}_{Y=0}+\mathcal{O}\left({ϵ}^3\right),$$

(27)

with the stresses $S_{i2}$ defined by Equation (13). Alternatively, the effective conditions, valid up to second order in $ϵ$, may be written in the following dimensional form:

$${\left.{\left.\widehat{u}\right|}_0\approx {\widehat{\lambda }}_x\left(\frac{\partial \widehat{u}}{\partial \widehat{y}}+\frac{\partial \widehat{v}}{\partial \widehat{x}}\right)\right|}_0+{\left.\frac{{\hat{\mathcal{K}}}_{xy}^{itf}}{\mu }\frac{\partial }{\partial \widehat{x}}\left(-\widehat{p}+2\mu \frac{\partial \widehat{v}}{\partial \widehat{y}}\right)\right|}_0,$$

(28)

$${\left.{\left.\widehat{v}\right|}_0\approx \frac{{\hat{\mathcal{K}}}_{yy}}{\mu }\frac{\partial }{\partial \widehat{y}}\left(-\widehat{p}+2\mu \frac{\partial \widehat{v}}{\partial \widehat{y}}\right)\right|}_0-{\left.{\hat{\mathcal{K}}}_{xy}^{itf}\frac{\partial }{\partial \widehat{x}}\left(\frac{\partial \widehat{u}}{\partial \widehat{y}}+\frac{\partial \widehat{v}}{\partial \widehat{x}}\right)\right|}_0-{\left.{\hat{\mathcal{K}}}_{zy}^{itf}\frac{\partial }{\partial \widehat{z}}\left(\frac{\partial \widehat{w}}{\partial \widehat{y}}+\frac{\partial \widehat{v}}{\partial \widehat{z}}\right)\right|}_0,$$

(29)

$${\left.{\left.\widehat{w}\right|}_0\approx {\widehat{\lambda }}_z\left(\frac{\partial \widehat{w}}{\partial \widehat{y}}+\frac{\partial \widehat{v}}{\partial \widehat{z}}\right)\right|}_0+{\left.\frac{{\widehat{\mathcal{K}}}_{zy}^{itf}}{\mu }\frac{\partial }{\partial \widehat{z}}\left(-\widehat{p}+2\mu \frac{\partial \widehat{v}}{\partial \widehat{y}}\right)\right|}_0,$$

(30)

where the dimensional model coefficients are defined by introducing the length microscale $l=ϵH$, as follows:

$${\widehat{\lambda }}_{x,z}={\lambda }_{x,z}l,{\widehat{\mathcal{K}}}_{xy,zy}^{itf}={\mathcal{K}}_{xy,zy}^{itf}{l}^2,{\widehat{\mathcal{K}}}_{yy}={\mathcal{K}}_{yy}{l}^2.$$

(31)

2.5. The Role of the Porosity: Parametric Study

The values of the model coefficients have already been stated in (24) for the specific case of streamwise-aligned cylinders with a porosity of 0.5; however, it is practically advantageous to generate a database of these geometry-dependent parameters to cover a wide range of $\theta$, so that the model can be directly implemented in optimization studies at a future stage. A range of $0.215\le \theta \le 0.99$ is considered in the parametric analysis. The values of the upscaled coefficients have been estimated, following the numerical procedure described earlier in Section 2.3. The results are listed in

Table 1. Numerical values of the macroscopic coefficients at different values of the porosity, for the case of longitudinal cylindrical inclusions.

$\mathit{\theta }$	${\mathit{\lambda }}_{\mathit{x}}$	${\mathit{\lambda }}_{\mathit{z}}$	${\mathcal{K}}_{\mathbf{yy}}={\mathcal{K}}_{\mathbf{zz}}$	${\mathcal{K}}_{\mathbf{xx}}$	${\mathcal{K}}_{\mathbf{xy}}^{\mathbf{itf}}$	${\mathcal{K}}_{\mathbf{zy}}^{\mathbf{itf}}$
0.215	5.883$\times {10}^{-2}$	4.103 $\times {10}^{-2}$	0	1.217 $\times {10}^{-3}$	3.814 $\times {10}^{-3}$	1.823 $\times {10}^{-3}$
0.500	6.883 $\times {10}^{-2}$	4.513 $\times {10}^{-2}$	1.828 $\times {10}^{-3}$	6.966 $\times {10}^{-3}$	5.561 $\times {10}^{-3}$	2.220 $\times {10}^{-3}$
0.600	7.398 $\times {10}^{-2}$	4.713 $\times {10}^{-2}$	4.331 $\times {10}^{-3}$	1.212 $\times {10}^{-2}$	6.737 $\times {10}^{-3}$	2.410 $\times {10}^{-3}$
0.700	8.167 $\times {10}^{-2}$	4.992 $\times {10}^{-2}$	9.587 $\times {10}^{-3}$	2.222 $\times {10}^{-2}$	9.042 $\times {10}^{-3}$	2.657 $\times {10}^{-3}$
0.800	9.347 $\times {10}^{-2}$	5.385 $\times {10}^{-2}$	1.990 $\times {10}^{-2}$	4.179 $\times {10}^{-2}$	1.410 $\times {10}^{-2}$	2.965 $\times {10}^{-3}$
0.900	1.130 $\times {10}^{-1}$	6.010 $\times {10}^{-2}$	3.970 $\times {10}^{-2}$	8.031 $\times {10}^{-2}$	2.638 $\times {10}^{-2}$	4.113 $\times {10}^{-3}$
0.990	1.953 $\times {10}^{-1}$	8.912 $\times {10}^{-2}$	1.255 $\times {10}^{-1}$	2.534 $\times {10}^{-1}$	1.075 $\times {10}^{-1}$	2.960 $\times {10}^{-2}$

, and are graphically presented in Figure 4. The minimum possible value of the porosity ($\theta =0.215$) is related to a cylinder diameter equal to one; for this configuration, the physical interface between the channel flow and the porous substrate becomes impermeable in the wall-normal direction (${\mathcal{K}}_{yy}=0$), and the case of flow over semi-circular riblets (instead of a porous substrate) is retrieved. It can be realized from Figure 4 that all coefficients monotonically increase with $\theta$. It should be observed that high values of $\theta$ are not representative of typical porous media, aside from perhaps the case of sparse canopies.

3. The Macroscale Problem: Setup, Results and Discussion

This section is mainly dedicated to the macroscale problem concerning the turbulent channel flow over a porous substrate; the effective boundary conditions at the substrate/channel virtual interface, obtained in Section 2, are employed, with the macroscale coefficients corresponding to different configurations of the porous bed, for detecting, comparing and analyzing the skin-friction drag increase/reduction. The direct numerical simulation of the turbulent flow through a smooth, impermeable channel is conducted first (Section 3.1). The main objectives of this preliminary step are to (i) assess the accuracy of the CFD code, (ii) confirm the adequacy of the domain size and the grid by means of extensive validation using the rich literature on smooth channel flow, and (iii) provide baseline results to which the main statistics of channel flows over permeable walls are later compared (Section 3.2).

3.1. Channel Flow with Smooth, Impermeable Walls

3.1.1. Simulation Definition and Numerical Schemes

The computational domain is sketched in Figure 5a. The dimensions in the streamwise direction ($L_X$), the wall-normal direction ($L_Y$) and the spanwise direction ($L_Z$) are normalized with half the channel height (H); $L_Y=2$ by definition, while the values $L_X\approx 2\pi$ and $L_Z\approx \pi$ are chosen. The no-slip/no-transpiration boundary condition are enforced at the upper and lower walls ($U=V=W=0$). Since the flow is fully developed, periodic boundary conditions of the velocity vector and the pressure are used along the streamwise and spanwise directions (cf. Figure 5b). The flow is forced by a uniform volumetric momentum source term in the X-direction, with a value $M=1$; therefore, a wall shear stress ${\tau }_w$ of 1 (at lower and upper walls) is expected as the bulk balance between forces is reached. If the value of the fluid density in Equation (1) is $\rho =1$ and the dynamic viscosity is $\mu \approx 1/190$, the shear velocity $(u_{\tau }=\sqrt{{\tau }_w/\rho })$ is equal to 1 so that the friction Reynolds number ${\displaystyle (R{e}_{\tau }=\rho u_{\tau }H/\mu )}$ is approximately 190.

The governing equations are discretized with the finite volume method, as by the implementation of the Simcenter STAR-CCM+ multiphysics software (version 16.02.009-R8). The hybrid MUSCL 3rd-order/central-differencing scheme was employed for spatial discretization. The scheme combines boundedness and accuracy; under smooth local flow conditions, it is formulated as a linear blend between a MUSCL 3rd-order upwind scheme and a 3rd-order central-differencing scheme, with an upwind blending factor equal to 0.1. The reader is referred to [43] for details on the MUSCL/CD approach. A structured three-dimensional grid was generated (Figure 5c). The mesh is uniform in streamwise and spanwise directions, where the respective spacings of the grid (in wall units) are $h_X^{+}\approx 9.47$ and $h_Z^{+}\approx 6.32$. The grid is gradually stretched in the wall-normal direction to obtain thinner elements near the walls ($h_Y^{+}\approx 0.29$) and thicker near the centerline ($h_Y^{+}\approx 8.25$). A second-order implicit scheme was used for temporal discretization. To maintain the maximum Courant number below 1, a time step of 0.0015 was applied (the time scale is ${\displaystyle \frac{H}{u_{\tau }}}$). The SIMPLE algorithm was used for pressure-velocity coupling.

Two critical points should be highlighted. First, the size of the computational domain is, in general, smaller than that used in some previous numerical studies. For instance, the dimensions $L_X=4\pi$ and $L_Z=\frac{4}{3}\pi$ were chosen in [4], while the dimensions $L_X=4\pi$ and $L_Z=2\pi$ were used in [44], compared to $L_X=2\pi$ and $L_Z=\pi$ in the present study. Second, the finite volume method used in this work is not the standard discretization approach followed in the literature dealing with the direct simulation of turbulent channel flow. The majority of previous studies adopted either a fully spectral Fourier–Chebyshev spatial discretization method [4,44,45] or a staggered high-order finite difference method [4,46,47]. The points above indicate that a comprehensive validation of the present setup is recommended.

3.1.2. Results and Validation

First, the simulation was run for about 130 time units to establish the turbulence perturbations and go beyond the initial transient of the flow field. The statistics were then averaged over almost 35 time units. The main convergence criterion is the bulk velocity ${\overline{U}}_b$, that is, the volume-averaged mean streamwise velocity over the channel (normalized by $u_{\tau }$). The bulk velocity ${\overline{U}}_b$ eventually converged to a value of $15.688$ (meaning that the bulk Reynolds number is $Re\approx 2981$), compared to ${\overline{U}}_b=15.70$ in [4] and ${\overline{U}}_b=15.73$ in [46]. The corresponding values of the skin-friction drag coefficient ($C_f$), based on ${\overline{U}}_b$, are: 0.00813 (present), 0.00811 [4], and 0.00808 [46]. The statistics given below at any distance Y from the wall have been evaluated via spatial averaging over the corresponding $X-Z$ plane.

• Mean velocity profile:

The distribution of the mean streamwise velocity ($\overline{U}$) is displayed in Figure 6 as a function of the normal distance (Y) from the lower wall. It is clear that the present numerical results for $\overline{U}$ agree well with the reference results by Vreman and Kuerten [4] and Kim et al. [44]. For instance, the value of the centerline velocity ${\overline{U}}_c$ is equal to 18.3, compared to approximately 18.28 in [4] and 18.18 in [44]. The velocity profile is plotted in wall coordinates in Figure 7-left; $Y^{+}=YR{e}_{\tau }$. The behavior fits well with the linear relation $\overline{U}=Y^{+}$ in the viscous sublayer (up to $Y^{+}\approx 5$), while the log law, $\overline{U}=(1/\kappa )ln{Y}^{+}+B$, is satisfied for $Y^{+}⪆40$. Here, the von Kármán constant ($\kappa$) is $0.4$, while a value of $5.5$ was chosen for the intercept of the logarithmic profile (B) to take into account the low Reynolds number effect [44]. The behavior of the log-law diagnose function, defined as ${\displaystyle \Xi =Y^{+}\frac{\partial \overline{U}}{\partial Y^{+}}}$, is shown in Figure 7-right. The constancy of $\Xi$ indicates, by definition, a typical logarithmic behavior of $\overline{U}$, where the constant value $\Xi \approx 2.5$ corresponds to the coefficient $1/\kappa$. It is clear that the upper validity limit of the log-law is $Y^{+}\approx 125$.

• Turbulence statistics:

It is useful for both validation and physical interpretation purposes to analyze the primary fluctuations ($U^{\prime },V^{\prime },W^{\prime }$), representing the instantaneous deviations of the velocity components from their time-averaged values; for example, $U^{\prime }=U-\overline{U}$. The intensity of the fluctuations can be described by the root-mean-square ($rms$) values ($U_{rms},V_{rms},W_{rms}$), where $U_{rms}={\overline{U^{\prime }{U}^{\prime }}}^{1/2}$, for example. Another measure is the intensity of the fluctuations (${\displaystyle I_u=\frac{U_{rms}}{\overline{U}},I_v=\frac{V_{rms}}{\overline{U}},I_w=\frac{W_{rms}}{\overline{U}}}$). The behaviors of both estimates ($rms$, I) are show in wall coordinates in Figure 8, together with reference data from [4,44]; the accuracy of the present results is confirmed.

The Turbulent Kinetic Energy (TKE) is defined as ${\displaystyle k=\frac{1}{2}(\overline{U^{\prime }{U}^{\prime }}+\overline{V^{\prime }{V}^{\prime }}+\overline{W^{\prime }{W}^{\prime }})}$. The dissipation terms in the transport equations of ${\displaystyle \overline{U^{\prime }{U}^{\prime }},\overline{V^{\prime }{V}^{\prime }},\overline{W^{\prime }{W}^{\prime }}}$ are plotted in wall coordinates in Figure 9-left. They are defined, in dimensionless forms, as follows:

$$({ϵ}_u,{ϵ}_v,{ϵ}_w)=\frac{2}{R{e}_{\tau }^2}(\overline{|\nabla U^{\prime }{|}^2},\overline{|\nabla V^{\prime }{|}^2},\overline{|\nabla W^{\prime }{|}^2}),$$

(32)

with the gradients of the primary fluctuations calculated using the dimensionless space variables ($X,Y,Z$). The total dissipation and production rates of TKE are approximately balanced within the log-law region, as can be realized from Figure 9-right. They are defined in dimensionless forms as:

$${ϵ}_T=\frac{1}{2}({ϵ}_u+{ϵ}_v+{ϵ}_w),$$

(33)

$$P_T=-\frac{1}{R{e}_{\tau }}\overline{U_i^{\prime }{U}_j^{\prime }}\frac{\partial \overline{U_i}}{\partial X_j}.$$

(34)

One of the observables most focused upon in wall turbulence is the Reynolds stress tensor, ${\mathbf{\tau }}^{\mathit{R}}$, and in particular the component ${\tau }_{xy}^R$ is the most relevant to skin-friction drag. The total stress is defined as the sum of viscous and Reynolds stresses, that is, ${\tau }_{xy}={\tau }_{xy}^V+{\tau }_{xy}^R$. With $\rho u_{\tau }^2$ as scale, the dimensionless stresses are given by ${\displaystyle {\tau }_{xy}^V=\frac{1}{R{e}_{\tau }}\frac{\partial \overline{U}}{\partial Y}}$ and ${\displaystyle {\tau }_{xy}^R=-\overline{U^{\prime }{V}^{\prime }}}$. The good agreement between the present results and those by Kim et al. [48], shown in Figure 10, further attests to the validity of the finite volume model employed here, and the suitability of the numerical setup.

3.2. Turbulent Flow over Porous Substrates

3.2.1. Basic Definitions and Implementation of the Effective Conditions

The turbulent channel flow over porous substrates of different microstructures is macroscopically analyzed in this section, with the aid of the homogenization model described in Section 2. The numerical procedure, including the spatial and the temporal discretization schemes and the $X-$momentum forcing term, is identical to the setup of the smooth channel case, described in Section 3.1.1. The only modification is that the lower boundary (at $Y=0$) now mimics a slip, permeable wall. This can be achieved by implementing the effective boundary conditions for the three velocity components given in Equations (25)–(27), with model coefficients corresponding to the specific topology and orientation of the solid inclusions sketched in Figure 11. Focus is on the evaluation and the further interpretation of the favorable/adverse changes in the skin-friction drag, related to the presence of different anisotropic permeable substrates. It is important to highlight that the geometries of the inclusions described in Figure 11 are intentionally chosen to meet this objective. The inclusions considered are: (i) transverse, Z-aligned, cylinders (configuration: TC); (ii) longitudinal, X-aligned, cylinders (configuration: LC); (iii) longitudinal cylindrical elements modified with four longitudinal protrusions in the shape of parallelepipeds, equally spaced along the circumference (configuration: LM). The dimensions of the solid inclusion within the unit cell are chosen to yield the same porosity, $\theta =0.5$. The model coefficients for substrate LC have been estimated earlier; they are given in (24). The coefficients for the case of spanwise-aligned cylinders (TC) are directly available from the LC case, by simply switching the streamwise and spanwise coordinates, i.e.,

$$\begin{array}{c}{\lambda }_x=0.04513,{\lambda }_z=0.06883,{\mathcal{K}}_{xy}^{itf}=0.002220,{\mathcal{K}}_{zy}^{itf}=0.005561,\\ {\mathcal{K}}_{xx}=0.001828,{\mathcal{K}}_{yy}=0.001828,{\mathcal{K}}_{zz}=0.006966.\end{array}$$

(35)

Conversely, configuration LM requires the numerical solution of the ad hoc problems given in Section 2.2 for this specific geometry: the dimensionless upscaled coefficients are found to be

$$\begin{array}{c}{\lambda }_x=0.1130,{\lambda }_z=0.0590,{\mathcal{K}}_{xy}^{itf}=0.01213,{\mathcal{K}}_{zy}^{itf}=0.00411,\\ {\mathcal{K}}_{xx}=0.00762,{\mathcal{K}}_{yy}=0.000121,{\mathcal{K}}_{zz}=0.000121.\end{array}$$

(36)

It should be noted that by modifying the longitudinal geometry with the addition of four thin fins we have been able to increase the difference between ${\lambda }_x$ and ${\lambda }_z$; in light of literature results (presented in Section 1) this is expected to improve the drag-reducing effect of the porous layer.

The last parameter which needs to be set is $ϵ=l/H$. Two values were tested: (i) $ϵ=0.05$, with the substrates indicated as $T{C}_5,L{C}_5,L{M}_5$; (ii) $ϵ=0.10$, with the substrates denoted by $T{C}_{10},L{C}_{10},L{M}_{10}$. For later discussion, it is also useful to define the model coefficients in wall units, with the slip coefficients ($\lambda$) multiplied by ($ϵR{e}_{\tau }$) and the permeabilities (${\mathcal{K}}^{inf},\mathcal{K}$) multiplied by ${\left(ϵR{e}_{\tau }\right)}^2$; the numerical values of these parameters are given in

Table 2. Values of the macroscopic coefficients for the different configurations of the porous substrate, given in wall units with $R{e}_{\tau }\approx 190$.

Macroscopic Parameters	Configurations
	${\mathit{TC}}_{\mathbf{5}}$	${\mathit{LC}}_{\mathbf{5}}$	${\mathit{LM}}_{\mathbf{5}}$	${\mathit{TC}}_{\mathbf{10}}$	${\mathit{LC}}_{\mathbf{10}}$	${\mathit{LM}}_{\mathbf{10}}$
${\lambda }_x^{+}$	0.4287	0.6539	1.0735	0.8574	1.3078	2.1470
${\lambda }_z^{+}$	0.6539	0.4287	0.5605	1.3078	0.8574	1.1210
${\mathcal{K}}_{xy}^{inf,+}$	0.2004	0.5018	1.0947	0.8016	2.0072	4.3788
${\mathcal{K}}_{zy}^{inf,+}$	0.5018	0.2004	0.3709	2.0072	0.8016	1.4836
${\mathcal{K}}_{xx}^{+}$	0.1650	0.6287	0.6877	0.6600	2.5148	2.7508
${\mathcal{K}}_{yy}^{+}$	0.1650	0.1650	0.0109	0.6600	0.6600	0.0436
${\mathcal{K}}_{zz}^{+}$	0.6287	0.1650	0.0109	2.5148	0.6600	0.0436

, for all the substrates defined.

Numerically enforcing the effective boundary conditions (25)–(27) is a delicate task for several reasons. First, the pressure-gradient term ${\displaystyle {\left.\frac{\partial P}{\partial X}\right|}_{Y=0}}$, present at second order in $ϵ$ in the definition of the streamwise slip velocity, may be decomposed into a mean term and a fluctuating part. The mean pressure gradient ${\displaystyle {\left.\frac{\partial \overline{P}}{\partial X}\right|}_{Y=0}}$ corresponds to the $X-$momentum volumetric source term ($M=1$), which forces fluid motion through the channel. Second, imposing a wall-normal, transpiration, velocity component may induce numerical instabilities, associated with an imbalance between blowing and suction at the $Y=0$ dividing surface. Hence, it is useful to define an ad hoc function, as part of the numerical code, to impose that the surface-averaged transpiration velocity at $Y=0$ vanishes at each time step. Furthermore, we have found it to be advantageous to seek an explicit expression of the transpiration-velocity condition (Equation (26)), by writing

$${\left.\frac{\partial S_{12}}{\partial X}\right|}_{Y=0}=\frac{1}{ϵ{\lambda }_x}{\left.\frac{\partial U}{\partial X}\right|}_{Y=0}+\mathcal{O}\left(ϵ\right),{\left.\frac{\partial S_{32}}{\partial Z}\right|}_{Y=0}=\frac{1}{ϵ{\lambda }_z}{\left.\frac{\partial W}{\partial Z}\right|}_{Y=0}+\mathcal{O}\left(ϵ\right).$$

(37)

The expressions above are immediately available from Equations (25) and (27). Finally, mass conservation can be used to replace $\left({\displaystyle \frac{\partial V}{\partial Y}}\right)$ by $\left({\displaystyle -\frac{\partial U}{\partial X}-\frac{\partial W}{\partial Z}}\right)$ in the definition of the outer-stress component $S_{22}$ in Equation (26).

3.2.2. Results for $ϵ=0.05$

Detailed results for the substrates $T{C}_5$, $L{C}_5$ and $L{M}_5$ are considered here; they will provide insight into the main parameters which control skin-friction drag.

The quantities that we intend to discuss in detail are first defined and summarized here. The flow under study is bounded by a lower permeable wall (at $Y=0$) and an upper smooth wall (at $Y=2$); hence, two different values of the total shear stress may be defined, i.e., ${\tau }_0$ and ${\tau }_2$, respectively. The ratio between the two stresses is ${\displaystyle S_R=\frac{{\tau }_0}{{\tau }_2}}$. The total shear stresses at the walls are linked to the $X-$momentum source term, M, on account of the balance of forces in the $X-$direction; that is, ${\tau }_0+{\tau }_2=2M$. Here, a major parameter in the following discussions is defined, the source-term-based stress: ${\displaystyle {\tau }_M=M=\frac{{\tau }_0+{\tau }_2}{2}}$. In the present case it is ${\tau }_M=1$ for all simulations and the friction Reynolds number, based on ${\tau }_M$, is equal to 190, as in the smooth channel case.

The drag coefficient is also based on ${\tau }_M$ and the bulk velocity ${\overline{U}}_b$, as follows:

$$C_f=\frac{2{\tau }_M}{\rho {\overline{U}}_b^2}.$$

(38)

The percentage deviation of the drag coefficient from the reference value of the smooth channel is defined as:

$$\Delta C_f\%=\frac{C_{f,porous}-C_{f,smooth}}{C_{f,smooth}}\times 100(\%),$$

(39)

with a negative value of $\Delta C_f\%$ which indicates drag reduction (implying an increase in the flow rate), and vice versa when $\Delta C_f\%$ is positive.

The numerical values of $S_R$ and $\Delta C_f\%$, for the different configurations, are presented in

Table 3. Values of the total shear stress ratio between the lower and the upper walls (${\displaystyle S_R=\frac{{\tau }_0}{{\tau }_2}}$) and of the percentage change in the skin-friction drag coefficient ($\Delta C_f\%$).

Quantities	Configurations
	Smooth	${\mathit{TC}}_5$	${\mathit{LC}}_5$	${\mathit{LM}}_5$
$S_R$	1	1.036	0.976	0.961
$\Delta C_f\%$	0	+2.423%	−2.157%	−3.681%

. The results show that drag reduction is achieved by the configurations $L{C}_5$ and $L{M}_5$, which are characterized by preferential orientation of the solid inclusions in the streamwise direction, with ${\mathcal{K}}_{xx}^{+}>{\mathcal{K}}_{zz}^{+}$, ${\lambda }_x^{+}>{\lambda }_z^{+}$ and ${\mathcal{K}}_{xy}^{inf,+}>{\mathcal{K}}_{zy}^{inf,+}$ (cf. Table 2). This concept is well established in the literature of drag reduction by small surface manipulations [26,27,31], in particular for porous substrates wall-normal permeability ${\mathcal{K}}_{yy}^{+}$ too small to initiate a Kelvin–Helmholtz instability in the turbulent boundary layer. The drag reduction is more pronounced for the substrate $L{M}_5$, a fact probably correlated to the accrued difference between ${\lambda }_x^{+}$ and ${\lambda }_z^{+}$, as anticipated. It is also clear that drag reduction is associated with values of $S_R$ lower than 1, which means that the total shear stress at the permeable wall ($Y=0$) is smaller than its value at the upper smooth surface.

A summary of interfacial and peak values of a few observables is provided in

Table 4. Interfacial and peak values of the mean velocity and of turbulence-characterizing parameters for different configurations of the porous medium ($\theta =0.5$ and $ϵ=0.05$). The peak values are those closer to the permeable surface. For reference, also the results for a smooth channel are given.

Quantity	Interfacial Values (Y = 0)				Peak Values
	Smooth	${\mathit{TC}}_5$	${\mathit{LC}}_5$	${\mathit{LM}}_5$	Smooth	${\mathit{TC}}_5$	${\mathit{LC}}_5$	${\mathit{LM}}_5$
$\overline{U}$	0	0.4439	0.6605	1.0719	18.164	17.959	18.397	18.446
$U_{rms}$	0	0.1829	0.2388	0.3643	2.6359	2.6377	2.6102	2.5668
$V_{rms}$	0	0.0135	0.0078	0.0082	0.8292	0.8427	0.8184	0.8097
$W_{rms}$	0	0.1462	0.0876	0.1152	1.0692	1.0879	1.0529	1.0598
${\tau }_{xy}^R$	0	0.00081	0.00046	0.00064	0.7231	0.7521	0.7069	0.7023
$I_u$	0.3660	0.4120	0.3615	0.3399	0.3660	0.4120	0.3615	0.3399
$I_w$	0.2000	0.3293	0.1326	0.1075	0.2000	0.3293	0.1485	0.1297
${ϵ}_T$	0.1680	0.2055	0.1567	0.1393	0.1680	0.2055	0.1567	0.1393

for all configurations considered so far. These results will be later referred to while discussing and comparing the behaviors of the different flow cases.

• Mean velocity profiles.

The profiles of the mean streamwise velocity ($\overline{U}$) across the channel are displayed in Figure 12. The behavior of the slip velocity at the fictitious $Y=0$ wall is highlighted in the lower frame of the figure, and compared to the solution obtained by enforcing no-slip conditions at both surfaces. A preliminary estimation of the value of the slip velocity can be obtained from the first-order term in the effective boundary condition of U, Equation (25), which may be recast in terms of the mean velocity ($\overline{U}$) and the wall distance in viscous units ($Y^{+}$) as follows:

$${\left.\overline{U}\right|}_{Y=0}\approx {\left.{\lambda }_x^{+}\frac{\partial \overline{U}}{\partial Y^{+}}\right|}_{Y=0}.$$

(40)

With the velocity gradient ${\displaystyle {\left.\frac{\partial \overline{U}}{\partial Y^{+}}\right|}_{Y=0}}$ equal to 1, Equation (40) simplifies to a Dirichlet boundary condition, i.e.,

$${\left.\overline{U}\right|}_{Y=0}\approx {\lambda }_x^{+}.$$

(41)

A comparison between the interfacial values of $\overline{U}$, in Table 4, and the corresponding values of ${\lambda }_x^{+}$, in Table 2, confirms the approximate result of Equation (41), with minor deviations which can be attributed to second-order terms and to the fact that the shear velocity used as scale is calculated based on the momentum source term (M) and not on ${\tau }_0$ (cf. Section 3.2.2).

The mean velocity profiles are plotted in wall coordinates in Figure 13, up to the centerline of the channel ($Y^{+}=R{e}_{\tau }\approx 193$). A better vision of the boundary layer characteristics through the logarithmic region is available. The behavior of the velocity profiles follows the classical theory of near-wall turbulence, according to which the surface alterations only affect the intercept of the logarithmic profile, while the von Kármán constant ($\kappa \approx 0.4$) remains constant [27,49]. Hence, a general expression of the velocity distribution in the log-law region may be written as follows:

$$\overline{U}={\displaystyle \frac{1}{\kappa }}ln{Y}^{+}+B+\Delta \overline{U},$$

(42)

with B the intercept in the case of a smooth wall, and $\Delta \overline{U}$ the shift of the velocity profile from the corresponding smooth channel behavior. The variations in $\Delta \overline{U}$ across the boundary layers over different substrates are shown in the right frame of Figure 13. As expected, the logarithmic regions ($30\le Y^{+}\le 120$) are characterized by approximately constant values of $\Delta \overline{U}$ (corresponding to parallel profiles of $\overline{U}$); which can be directly linked to the deviations of the skin-friction drag coefficients from the smooth channel case; a positive value of $\Delta \overline{U}$ implies drag reduction (as for substrates $L{C}_5$ and $L{M}_5$), and vice versa for substrate $T{C}_5$.

• Turbulence statistics.

A better understanding of the drag reduction mechanism is sought by the analysis of turbulence statistics near the permeable walls. The definitions of all the parameters under consideration here are the same as in Section 3.1.2.

The root-mean-squares of the velocity fluctuations are plotted in Figure 14 near the different permeable walls. A wall-normal range $0\le Y^{+}\le 75$ is used to display the distributions of $U_{rms},V_{rms}$ and $W_{rms}$, where significant features and deviations from the no-slip case are highlighted. In particular, the values of the RMS fluctuations at the interface with the porous substrates deviate from zero, as quantified in Table 4, owing to the slip/transpiration boundary in $Y=0$. The interfacial values of $U_{rms}$ and $W_{rms}$ appear to be directly correlated to ${\lambda }_x^{+}$ and ${\lambda }_z^{+}$, respectively (compare the corresponding values in Table 2 and Table 4). Proceeding towards the logarithmic region, the deviation of $U_{rms},V_{rms}$ and $W_{rms}$ from the smooth channel behavior yields some insight onto the ability of the substrates $L{C}_5$ and $L{M}_5$ to attenuate turbulence in the near-wall layer. This might explain the drag reduction caused by these longitudinal configurations, in comparison to the adverse effect of the spanwise-aligned inclusions, substrate $T{C}_5$. This can be confirmed by comparing the values of the percentage changes in skin-friction drag (Table 3) and the peak values of the rms velocity fluctuations (Table 4). The preceding concept applies also to the distributions of the Reynolds shear stress ${\tau }_{xy}^R$; cf. Figure 15. An increase in the peak value of ${\tau }_{xy}^R$ by about $4\%$ is realized for the substrate $T{C}_5$; this implies destabilization of the turbulent boundary layer overlying the transverse cylinders, which adversely affects skin-friction drag. Conversely, the production of Reynolds stresses in the logarithmic region is slightly mitigated by the configurations $L{C}_5$ and $L{M}_5$. It should be noted that the values of the Reynolds shear stress at the permeable walls (cf. Table 4) are too small to be graphically captured; this may be ascribed to the low values of the wall-normal permeability, ${\mathcal{K}}_{yy}^{+}$.

The distributions of the turbulence intensities $I_u$ and $I_w$ are shown in Figure 16 in the neighborhood of the permeable walls, i.e., up to $Y^{+}\approx 9$. Interestingly, the behaviors of these quantities, even at the permeable wall and within the adjacent viscous sublayer, are strongly linked to the corresponding changes in the skin-friction drag. The same concept applies to the turbulence dissipation (${ϵ}_T$), displayed in Figure 17. For instance, the drag increase in the case of the substrate $T{C}_5$ is associated with increase in the interfacial values (at $Y=0$) of $I_u$, $I_w$ and ${ϵ}_T$ by about $13\%$, $60\%$ and $40\%$, respectively, whereas these parameters decrease by about $7\%$, $45\%$ and $17\%$ for the substrate $L{M}_5$. This should be compared to the RMS of the velocity fluctuations, which proved to be representative of changes in the skin-friction drag coefficient only in the log-law region.

3.2.3. Results for $ϵ=0.1$

The turbulent channel flow ($R{e}_{\tau }\approx 190$) over permeable walls of periodicity ($ϵ$) equal to 0.1 is analyzed in this section; the porous substrates $T{C}_{10}$ and $L{M}_{10}$ are specifically considered. In principle, by increasing the value of $ϵ$ (with respect to the case $ϵ=0.05$ examined in Section 3.2.2), the differences between the slip lengths ${\lambda }_x^{+}$ and ${\lambda }_z^{+}$ are more significant (cf. Table 2), and the adverse/favorable changes in the skin-friction drag coefficient are expected to be more pronounced. This concept is confirmed by the homogenization-based numerical results of the percentage change in the drag coefficient ($\Delta C_f\%$), presented in

Table 5. Values of the total shear stress ratio between the lower and the upper walls (${\displaystyle S_R=\frac{{\tau }_0}{{\tau }_2}}$) and the percentage change in the skin-friction drag coefficient ($\Delta C_f\%$), with the porous substrates characterized by $ϵ=0.1$.

Quantities	Configurations
	Smooth	${\mathit{TC}}_{10}$	${\mathit{LM}}_{10}$
$S_R$	1	1.150	0.953
$\Delta C_f\%$	0	+8.976%	−4.934%

. As can be realized, the substrate $L{M}_{10}$, with ${\lambda }_x^{+}>{\lambda }_z^{+}$, allows for approximately $5\%$ reduction in the skin-friction coefficient, whereas the drag coefficient increases by almost $9\%$ in the case of the substrate $T{C}_{10}$, for which ${\lambda }_z^{+}>{\lambda }_x^{+}$. The preceding values should be compared to a reduction by $3.68\%$ and an increase by $2.42\%$ with the substrates $L{M}_5$ and $T{C}_5$, respectively. It is clear that the increase in the skin-friction drag coefficient with substrate $T{C}_{10}$ is associated to a significant increase in the shear stress ratio ($S_R$), in the sense that the total shear stress at the lower permeable wall (${\tau }_0$) is much larger than its value at the upper smooth wall (${\tau }_2$).

The interfacial and the peak values of different quantities of interest over the substrates $T{C}_{10}$ and $L{M}_{10}$ are summarized in

Table 6. Interfacial and peak values of the mean velocity and different turbulence-characterizing parameters, for two different configurations of the porous medium (with $ϵ=0.1$).

Quantity	Interfacial Values ($\mathit{Y}=0$)			Peak Values
	Smooth	${\mathit{TC}}_{10}$	${\mathit{LM}}_{10}$	Smooth	${\mathit{TC}}_{10}$	${\mathit{LM}}_{10}$
$\overline{U}$	0	0.9404	2.1573	18.164	17.5436	18.5930
$U_{rms}$	0	0.4615	0.7129	2.6359	2.6106	2.5090
$V_{rms}$	0	0.0589	0.0360	0.8292	0.8842	0.8044
$W_{rms}$	0	0.3563	0.2667	1.0692	1.1615	1.0688
${\tau }_{xy}^R$	0	0.0108	0.0053	0.7231	0.7960	0.7053
$I_u$	0.3660	0.4900	0.3303	0.3660	0.4900	0.3303
$I_w$	0.2000	0.3691	0.1238	0.2000	0.3691	0.1287
${ϵ}_T$	0.1680	0.3168	0.1493	0.1680	0.3168	0.1493

; they may be compared to the values of the same quantities with $ϵ=0.05$, given in Table 4. The correspondence between the values of the mean streamwise velocity ($\overline{U}$) at the interface ($Y=0$) and the values of ${\lambda }_x^{+}$, given in Table 2, are still in line with the approximate relation (41), taking into account that, due to the increase in $ϵ$, the second-order terms in the effective boundary condition for U are now more pronounced. The effect of the $\mathcal{O}\left({ϵ}^2\right)$ terms is more apparent in the fluctuations of the transpiration velocity which is, by definition, a second-order effective boundary condition (cf. Equation (26)); the values of $V_{rms}$, given in Table 6, are more than four times the corresponding values found at $ϵ=0.05$.

The profiles of the mean streamwise velocity ($\overline{U}$) over the permeable substrates $T{C}_{10}$ and $L{M}_{10}$ are displayed in Figure 18. It is clear that the positive/negative deviations ($\Delta \overline{U}$) in the intercept of the logarithmic profile (cf. Equation (42)) are accentuated with respect to the corresponding cases with $ϵ=0.05$ (cf. Figure 13); this goes along with the larger changes in the drag coefficient at $ϵ=0.1$. In agreement with the previous discussion in Section 3.2.2, the turbulence intensities, presented in Figure 19, provide a fair clarification of the levels of disturbances in the near-wall layer, which can justify the adverse/favorable changes in skin friction coefficient for substrates $T{C}_{10}$ and $L{M}_{10}$, respectively.

4. Conclusions

The high skin-friction drag characterizing wall-bounded turbulent flows adversely affects the efficiency of fluid transportation systems. It is thus important to develop effective drag reduction strategies, e.g., properly engineered passive flow control surfaces/substrates. In the present work, turbulent channel flows over transversely isotropic permeable beds of different types were numerically studied, and the consequent favorable/adverse changes in the skin-friction drag coefficient were monitored and described by analyzing turbulence statistics.

A multiscale homogenization approach was introduced to avoid the numerical complexity and the expensive mesh requirements of a full resolution of the flow within the porous media. Expressions for the effective boundary conditions of the three velocity components were sought at a fictitious interface between the channel flow and the porous bed, up to second-order accuracy in terms of a small parameter ${\displaystyle ϵ=\frac{l\left(\mathrm{porous}\mathrm{pattern}\mathrm{periodicity}\right)}{H\left(\mathrm{half}\mathrm{channel}\mathrm{height}\right)}}$. The upscaled coefficients appearing in the definition of the effective boundary conditions, i.e., the slip lengths (${\lambda }_x,{\lambda }_z$), the medium permeability in the wall-normal direction (${\mathcal{K}}_{yy}$) and the interfacial permeabilities (${\mathcal{K}}_{xy}^{inf},{\mathcal{K}}_{zy}^{inf}$), were numerically calculated for three microstructures of the porous substrate. In particular, the microstructures considered were: ($TC$) transverse, Z-aligned, plain cylinders; ($LC$) longitudinal, X-aligned plain cylinders; ($LM$) longitudinal, X-aligned, cylinders modified by the addition of four fins on the circumference, especially designed to amplify the quantity (${\lambda }_x-{\lambda }_z$) while reducing the medium permeability, ${\mathcal{K}}_{yy}$.

Direct numerical simulations of the macroscale problem above the virtual interface with the different porous beds have been conducted, employing the finite volume method with the Hybrid MUSCL 3rd-order/central-differencing discretization scheme, initially validated on the flow through a smooth channel. A value of $ϵ=0.05$ was first employed, in order to focus on relatively small surface protrusions; the flow over the substrates $T{C}_5$, $L{C}_5$ and $L{M}_5$ was numerically studied, and the turbulence statistics were analyzed in detail. Secondly, the value of $ϵ$ was increased to $0.10$ for the substrates $T{C}_{10}$, $L{M}_{10}$, and the consequent changes in the skin-friction drag coefficient and other flow metrics of interest were examined. Clearly, the gauge factor $ϵ$ cannot be increased too much for the asymptotic expansion to remain valid. The range of validity of the approach, in terms of acceptable values of $ϵ$, will be investigated in future work. The major findings of the present study are summarized below:

(i)

The permeable substrates with preferential slip in the streamwise direction (${\lambda }_x^{+}>{\lambda }_z^{+}$), i.e., those designed with longitudinal (either plain or modified) cylinders, are able to reduce skin-friction drag. This conclusion should hold up to some critical value of ${\mathcal{K}}_{yy}$ at which large-scale instabilities have their onset in the near-wall layer [31].

(ii)

The adverse/favorable changes in the skin-friction drag coefficient are more pronounced for the substrates with $ϵ=0.1$. The drag coefficient increases by almost $9\%$ with the substrate $T{C}_{10}$, while about $5\%$ drag reduction is obtained with the substrate $L{M}_{10}$.

(iii)

The analysis of the turbulence intensities $I_u$ and $I_w$ provides a meaningful picture of the levels of disturbances in the neighborhood of the permeable walls; such intensities can be used, together with the streamwise slip velocity, to interpret changes in skin-friction drag.

(iv)

The implementation of the homogenization approach significantly reduces the numerical cost of direct numerical simulations over porous layers, since only the motion in the free-fluid region needs to be resolved. With the dimensions chosen for the domain, the total number of grid points is below $2\times {10}^6$, while the mesh requirements for a full feature-resolving simulation (including the porous substrate) may exceed ${10}^8$ (cf. Wang et al. [24]).

The present approximate framework needs to be properly validated against feature-resolving simulations which include the permeable medium, in order to provide full confidence in the model developed. This task is currently underway and preliminary results are encouraging. Once this validation phase is terminated, the homogenization model developed will be employed in a large-scale optimization study: different microstructures of the porous substrate will be examined in pursuit of the optimal topology, size and arrangement of the solid grains, capable to yield the largest skin-friction reduction. It will also be of interest to compare the homogenized results for porous substrates with inline and staggered arrangements of grains; this is the case since the configuration of randomly arranged inclusions might be expected to lie in between these two limiting cases, as observed by Naqvi and Bottaro [42].