A Review of the Main Process-Based Approaches for Modeling N₂O Emissions from Agricultural Soils

Abstract

Modeling approaches have emerged to address uncertainties arising from N₂O emissions variability, representing a powerful methodology to investigate the two emitting processes (i.e., nitrification and denitrification) and to represent the interconnected dynamics among soil, atmosphere, and crops. This work offers an extensive overview of the widely used models simulating N₂O under different cropping systems and management practices. We selected process-based models, prioritizing those with well-documented algorithms found in recently published scientific articles or having published source codes. We reviewed and compared the algorithms employed to simulate N₂O emissions, adopting a unified symbol system. The selected models (APSIM, ARMOSA, CERES-EGC, CROPSYST, CoupModel, DAYCENT, DNDC, DSSAT, EPIC, SPACSYS, and STICS) were categorized by the approaches used to model nitrification and denitrification processes, discriminating between implicit or explicit consideration of the microbial pool and according to the formalization of the main environmental drivers of these processes (soil nitrogen concentration, temperature, moisture, and acidity). Models’ setting and performance assessments were also discussed. From the appraisal of these approaches, it emerged that soil chemical–physical properties and weather conditions are the main drivers of N cycling and the consequent gaseous emissions.

1. Introduction

Commonly adopted agricultural practices aimed at improving cropping systems’ economic profitability have the potential to strongly influence, together with soil and environmental conditions, greenhouse gas (GHG) emissions, specifically those of carbon dioxide (CO₂) nitrous oxide (N₂O) and methane (CH₄) [1]. These GHGs have the potential to impact ozone chemistry (N₂O) and atmospheric oxidation status (CO₂) [2]. The concern about increasing N₂O emissions is related to its global warming potential, which is 265–298 times that of CO₂ for a 100-year time horizon [3]. Furthermore, N₂O is also considered the major stratospheric ozone-depleting substance. Agricultural practices, such as N amendment and fertilization, legume cropping, residue retention, and irrigation, tend to increase N₂O production and emission above background levels and contribute to indirect reactive nitrogen volatilization and nitrate leaching [4].

Soil N₂O emissions are influenced by the soil characteristics that affect primary processes that are indirectly or directly responsible for the emissions themselves: mineralization (indirectly), nitrification, and denitrification. Organic nitrogen, contained in crop residues and manure, is decomposed and mineralized by the soil microbial communities, resulting in the production of ammonium (NH₄⁺) [5]. During nitrification, which is operated by nitrifying bacteria and involves the oxidation of ammonium to nitrate (NO₃⁻) by key enzymes (e.g., ammonia monooxygenase, hydroxylamine dehydrogenase, nitric oxide oxidase, nitrite oxidoreductase) [6], a small proportion of N is lost as N₂O. In contrast, denitrification, conducted by denitrifying bacteria, involves the reduction of nitrate and nitrite to gaseous N₂ and N₂O [7], respectively, by nitrate and nitrite reductases [8]. Nitrification mainly occurs in well-aerated soils with moderate water content, while denitrification takes place in anaerobic conditions, mainly found in heavy soil with scarce drainage. The contribution of each process to N₂O emissions is controlled and limited by soil biogeochemical characteristics (soil texture, pH, temperature, moisture, oxygen accessibility, and microbial activity), environmental conditions, and the type and amount of applied N fertilizer [9]. Finer-textured soils tend to release higher amounts of N₂O compared to sandy soils [10]. This phenomenon can be attributed to the presence of predominant capillary pores in finer-textured soils, which retain water more effectively and create favorable conditions for N₂O emissions from denitrification [11,12]. Soil temperature is another key element that impacts N₂O emissions. An increase in soil temperature positively affects microbial growth but also reduces oxygen concentration, leading to an increase in anaerobic conditions [13,14]. Moreover, it was found that the N₂/N₂O ratio increased exponentially with the increasing temperature [15]. Soil acidity influences the N₂/N₂O ratio, too, but its effect on the nitrification and denitrification process needs further investigation [16].

Direct applications of N synthetic fertilizers increase the available pool for N cycle transformations [17]. As previous research reported [18], the time of fertilizer application influences the efficiency of fertilizer use and crop yield. When mineral fertilizer or manure is applied at rates greater than the effective crop need, N₂O emission can increase because of the large pool of soil N that cannot be assimilated by the crop and remains available for the biological transformations involved in N₂O production. Furthermore, N₂O emissions can be enhanced due to rainfall events that increase soil moisture [19,20]. Several strategies have been developed to reduce the amount of N available for soil microorganisms, thereby decreasing nitrification and denitrification rates [21], by reducing nitrogen fertilizer inputs and applying them precisely and strategically so that nitrogen supply becomes synchronized with a specific crop demand. Also, to increase the N efficiency and delay detrimental processes, the use of urease and nitrification inhibitors is recommended [16]. This alignment minimizes the portion of N in the soil and its potential losses through volatilization of NH₃, NO₃⁻ leaching, and N₂O emission [22].

Quantifying N₂O emissions from agricultural soils has always been challenging due to the significant spatial and temporal variations observed in this condition during field trials [23,24]. Several replications or integrations over a larger area are generally applied to capture the spatial variability at the field level, resulting from biological, chemical, and physical conditions of the soil [25]. Temporal variability in this context is assessed through several factors including measurement frequency, emission-related events timing, and the specific time of day when measurements are conducted [26,27,28].

In most research studies, direct N₂O flux measurements during field trials are conducted using either manual or automated chambers in combination with a gas chromatograph or infrared analyzer [29]. These measurement techniques are conducted at relatively small spatial domains, mostly plot scales, and are suitable to capture topographic and treatment effects on N₂O emissions [30]. They are cost effective and labor intensive but might effectively address the challenge of spatial variability on reported fluxes within the studied plot [31]. Automated chambers have the advantage of allowing frequent measurements of N₂O soil flux since this methodology is less time consuming and dependent on human intervention. They require less data gap filling than manual chambers, which are very manpower demanding [27]. Continuous measurements of N₂O fluxes at fine temporal scales (ranging from minutes to hours) are possible with the use of micrometeorological techniques [32,33] that are non-intrusive and suitable to overcome the inherent spatial variability in the process of soil N₂O emission while providing reliable and accurate high-frequency measurements of turbulent fluxes of GHGs. The most adopted approach by international ecological station networks (https://fluxnet.org/, accessed on 16 November 2023) is eddy covariance [34], a well-established method relying on fast-response sonic anemometers and spectrometers. Its use is widespread at larger spatial (between 100 m and several kilometers) and temporal scales (from hours to years) [35].

The abovementioned advancements in measurement techniques have unveiled a clear diurnal pattern in N₂O fluxes. This pattern, as observed in previous studies [36,37], implies that daily temperature variations and interactions between plants, soil microbial activities, and water content play significant roles in governing daily N₂O fluxes. Consequently, neglecting these diurnal variations could result in errors when estimating N₂O emissions. Chambers remain a valuable tool for measuring the impacts of soils, climate, and management on N₂O emissions from a range of sources. However, for pragmatic reasons, observational study periods usually cover only a few years under a narrow range of conditions and are often not continuous over that time [38]. In parallel, researchers use incubation experiments to gain a deeper understanding of nitrogen dynamics [39]. During these experiments, soil samples are analyzed under controlled conditions to assess the impact of factors such as soil moisture, texture, temperature, and various fertilization treatments on gas emissions [40]. The experiments conducted under incubation offer advantages in terms of experimental control and economic viability, but they may present some limitations, as the direct measure, in representing the real conditions of soil and agricultural environment [41]. Scale and representativeness restrictions are due to the typical small-scale trial conditions and difficulty in addressing real-world variability. Furthermore, the timeframe is commonly short and, therefore, not adequate to capture long-term trends and is not suitable for ex ante assessment [42].

To address the challenge of scaling up from an agricultural field to a regional level, improve accuracy and reproducibility, and estimate N losses associated with agricultural scenarios, various estimations’ methodologies and models have been devised, spanning from straightforward regression models to fully process-based ones [43]. Commonly, the choice between one of the various estimation and modeling approaches is related to the rationale of each study and the researcher’s level of familiarity with the available models, the agricultural system involved, and data requirements and availability [44]. The IPCC Guidelines for National Greenhouse Gas Inventories proposed a simplified estimation methodology that relates estimates of direct N₂O emissions from agricultural land to the quantities of nutrient N being applied [45,46]. This relation is defined by the emission factor, calculated for each type of input addition (mineral N fertilizer, organic manure, crop residue, and others) [46].

The models can either be empirical, derived from observed statistical or mathematical relationships, or process-based, developed to emulate the underlying process mechanisms [38]. Models of both types are also suitable to test hypotheses regarding biogeochemical process drivers and can be used to analyze the results of laboratory and field experiments [11]. While empirical approaches are limited to summarizing experimental data, process-based models mathematically represent one or several processes characterizing the functioning of well-delimited biological systems of fundamental or economic interest [47].

Process-based dynamic models simulate, at fine spatial and temporal scales, N₂O emissions by explicitly modeling the underlying biogeochemical processes that produce N₂O in soils and ecosystems, as influenced by pedoclimatic conditions and management practices. Data demand, which represents a common limitation [48,49], includes inputs such as soil properties, meteorological data, and cropping systems management practices, in addition to experimental observations required for model calibration and evaluation. Also, they often need site-specific information for accurate modeling [50,51,52]. The main advantage of using detailed input is the possibility of simulating daily soil conditions (soil temperature, soil water content, bulk density) and daily crop management (sowing and harvest, fertilization, irrigation, tillage). Indeed, process-based models’ time step is frequently 1 day, sometimes 1 h for submodels, which is appropriate to overcome the biogeochemical variation of agricultural systems that directly influence, as we reported above, the nitrification and denitrification processes. Another advantage of using detailed input data is the possibility of dividing the soil into discrete layers to describe management operations more finely (depth of soil tillage operation, fertilizer application, and crop residue burial). When differences in results arise from the application of simulation models, they can frequently be attributed to a lack of input data, to input data uncertainty, or to the inadequate resolution of biogeochemical processes. In these situations, model improvements in terms of algorithms and structure are recommended.

The aim of this work is to review and compare N₂O simulation approaches, with a major focus on dynamic process-based simulation models that provide a whole cropping system representation. A recently published and comprehensive review providing insights on the algorithms employed in the simulation of the N fluxes, particularly N₂O, is lacking. This work focuses on algorithm details reported for the selected models with a unified symbol system and is aimed at facilitating modeling approach comparisons and supporting algorithm implementation for further practical applications. In previous studies [53,54,55], process-based simulation approaches were successfully reviewed with, respectively, a major focus on model application scale (laboratory, field, and regional scale); model structure, strengths, and weaknesses; and emissions drivers representation (in three selected models). Comparing enforced algorithms for nitrification, denitrification, and GHG emissions provides an insightful tool for the analysis of the biogeochemical interactions concurring with N₂O emissions, thus allowing the evaluation of cropping system management practices’ impacts on these processes. A comparative overview of the performances of the selected models, based on common evaluation criteria as reported by authors, is also provided.

2. Materials and Methods

2.1. Literature Search Details

The objective of the present literature search was to review the main available modeling approaches for N₂O emissions simulation. Since only process-based models offer a detailed mechanistic understanding of the underlying processes responsible for N₂O emissions, the study remained focused on this type of approach while the other modeling methodologies are summarized in the Supplementary Materials. We constrained the study to the process-based models simulating nitrous oxide emissions in a cropping system environment, where such losses are of particular concern. The analysis was restricted to process-based models for which detailed documentation of algorithms was available, preferably in recently published scientific articles or in published source codes. Models who took part in international model comparison exercises or model ensemble projects were also preferred. The selection of the models was carried out based on (i) the availability of recently published and highly cited/used materials and (ii) the inclusion of the mathematical description/algorithms/mathematical functions of the system processes considered in each model for simulating N₂O. Among the process-based models emerging from the literature analysis, we specifically looked for those explicitly considering both nitrification and denitrification as contributors to N₂O emissions.

For each model, we reported the mathematical equations used to describe the key physiological process involved in N₂O emissions simulation. Concurrently, we also reviewed published materials relative to models’ application and evaluation for cropping system N₂O emissions simulation performance.

The literature search was conducted both on Scopus and Web of Science databases through the implementation of the following query:

(TITLE-ABS-KEY (model OR modeling OR simulate OR simulating OR simulation OR estimation OR estimate OR approach) AND ALL (N₂O OR nitrous AND oxide OR greenhouse AND gasses OR emission) AND TITLE-ABS-KEY (crop OR cropland AND soil OR agricultural AND environment) AND TITLE-ABS-KEY (flux OR fluxes OR emission)

As a result, we collected 439 papers on Scopus and 947 papers on the Web of Science. Another specific query has also been settled to identify scientific works where each model has been assessed considering its capability to simulate N₂O emissions in comparison to experimentally observed data. For this purpose, we added the terms (calibrate OR validation OR evaluation OR assessment) to the first query, and we obtained 134 papers in Scopus and 281 in Web of Science. From the results of both queries, redundant titles were removed, the topic was restricted to a model with a field scale approach and a daily timestep, and the abovementioned criteria were applied. Consequently, we selected 57 papers.

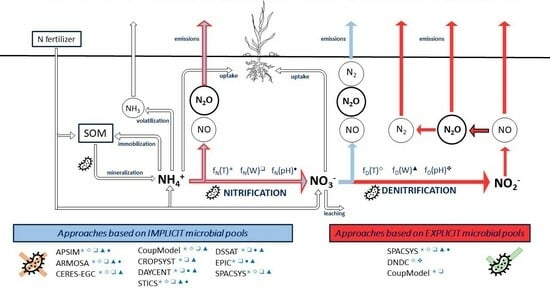
2.2. Overview of the Selected Models

The following process-based models (Table 1) were the result of the abovementioned selection activity. ARMOSA—Analysis of cRopping systems for Management Optimization and Sustainable Agriculture [56], APSIM—The Agricultural Production Systems sIMulator [57], CERES-EGC—Crop Environment REsource Synthesis—Environnement et Grandes Cultures [58], CROPSYST—Cropping Systems simulation model [59], and STICS—Simulateur mulTIdisciplinaire pour les Cultures Standard [60] are five dynamic models whose primary purpose is to operate as analytical tools aimed at the impact evaluation of cropping system management on both crop production and environment. They are able to simulate a range of critical processes such as crop growth, soil C and N dynamics, and soil and water management, including nitrogen transformation like net mineralization, nitrification, and denitrification processes.

DSSAT—Decision Support System For Agrotechnology Transfer [61] has been designed to address several application contexts such as genetic modeling, on-farm and precision management, and regional environmental assessments; thus, it supports a range of utilities comprising weather, soil, and genetics tools.

EPIC—Environmental Policy Integrated Climate model [62] is an agricultural dynamic model primarily developed to address the effect of soil erosion on crop productivity.

DNDC—DeNitrification-DeComposition [52,63] and DAYCENT—DAYly CENTury [64] are specially designed to simulate nitrogen and carbon fluxes, considering soil, crop, and water dynamics. CoupModel—Coupled heat and mass transfer model for soil–plant–atmosphere systems [65] was also designed to simulate water and heat fluxes; it has later adopted high-level submodules of nitrification, denitrification, and gas transport from DNDC [52]. Both feature a detailed microbial approach to trace gas emissions forms (e.g., N₂O, NO, N₂, NH₃, CH₄, and CO₂).

SPACSYS [66] is a process-based model simulating water, C, and N cycling between plants, soils, and microbes. It has been widely used to assess the impact of climate change tillage, fertilizer application, and different cultivars on agricultural systems in terms of crop yields, C and N budgets, soil physical properties, and soil water redistribution.

Table 1. Reviewed model overview. Nitrification simulation (Nit), denitrification simulation (Denit), microbial biomass explicit simulation, environmental factors considered: soil temperature (f(T)), soil moisture (f(W)), soil acidity (f(pH)), and substrate (other than ammonium and nitrate) concentration effect (f(substrate)).

Reference	Author	Year	Model	Nit	Denit	Microbial Biomass	f(T)	f(W)	f(pH)	f(substrate)
[67]	Thorburn et al.	2010	APSIM	yes	yes	no	yes	yes	only for Nit	active carbon only for Denit
[56]	Perego et al.	2013	ARMOSA	yes	yes	no	yes	yes	only for Nit	-
[58]	Gabrielle et al.	2005	CERES-EGC	yes	yes	no	yes	yes	no	-
[68]	Jansson and Karlberg	2010	CoupModel	yes	yes	optional for both Nit and Denit	yes	yes	yes	DOC for Nit in the microbial explicit approach
[69]	Stockle et al.	2012	CROPSYST	yes	yes	only for SOC mineralization	only for Nit	yes	only for Nit	CO2 for Denit
[11]	Parton et al.	2001	DAYCENT	yes	yes	no	only for Nit	yes	only for Nit	CO2 for Denit
[52]	Li	2000	DNDC	yes	yes	yes	yes	only for Nit	yes (indirectly for Nit)	indirectly DOC for both
[70]	Hoogenboom et al.	2019	DSSAT	yes	yes	no	only for CERES-Denit and Nit	yes	only for Nit	CO2 for DAYCENT-Denit, water-extractable C for CERES-Denit
[62]	Sharpley and Williams	1990	EPIC	yes	yes	no	yes	yes	only for Nit	CO2 for Denit (Kemanian option)
[71]	Wu et al.	2015	SPACSYS	yes	yes	optional for both Nit and Denit	yes	only for Nit	yes	DOC for Nit and Denit
[60]	Brisson et al.	2008	STICS	yes	yes	no	yes	yes	only for Nit	-

Table 1. Reviewed model overview. Nitrification simulation (Nit), denitrification simulation (Denit), microbial biomass explicit simulation, environmental factors considered: soil temperature (f(T)), soil moisture (f(W)), soil acidity (f(pH)), and substrate (other than ammonium and nitrate) concentration effect (f(substrate)).

Reference	Author	Year	Model	Nit	Denit	Microbial Biomass	f(T)	f(W)	f(pH)	f(substrate)
[67]	Thorburn et al.	2010	APSIM	yes	yes	no	yes	yes	only for Nit	active carbon only for Denit
[56]	Perego et al.	2013	ARMOSA	yes	yes	no	yes	yes	only for Nit	-
[58]	Gabrielle et al.	2005	CERES-EGC	yes	yes	no	yes	yes	no	-
[68]	Jansson and Karlberg	2010	CoupModel	yes	yes	optional for both Nit and Denit	yes	yes	yes	DOC for Nit in the microbial explicit approach
[69]	Stockle et al.	2012	CROPSYST	yes	yes	only for SOC mineralization	only for Nit	yes	only for Nit	CO2 for Denit
[11]	Parton et al.	2001	DAYCENT	yes	yes	no	only for Nit	yes	only for Nit	CO2 for Denit
[52]	Li	2000	DNDC	yes	yes	yes	yes	only for Nit	yes (indirectly for Nit)	indirectly DOC for both
[70]	Hoogenboom et al.	2019	DSSAT	yes	yes	no	only for CERES-Denit and Nit	yes	only for Nit	CO2 for DAYCENT-Denit, water-extractable C for CERES-Denit
[62]	Sharpley and Williams	1990	EPIC	yes	yes	no	yes	yes	only for Nit	CO2 for Denit (Kemanian option)
[71]	Wu et al.	2015	SPACSYS	yes	yes	optional for both Nit and Denit	yes	only for Nit	yes	DOC for Nit and Denit
[60]	Brisson et al.	2008	STICS	yes	yes	no	yes	yes	only for Nit	-

2.3. Statistical Indices for Model Evaluation

When reporting the application areas of the selected models, the evaluation criteria used by the authors and published in the articles were also included in this review. These evaluation indices were derived from experiments conducted for model validation and/or calibration. Typical statistical indices (Appendix A.1, Appendix A) for performance evaluations in modeling applications include Pearson’s correlation coefficient (r), coefficient of determination (R²), root mean squared error (RMSE), relative root mean squared error (RRMSE), and modeling efficiency (EF). These metrics describe the error associated with model estimates (RMSE), the total variation in observations captured by simulated data (R²), and whether the model outperforms a mean observation in the prediction of observed data (EF). When present, the other indexes have also been organized and reported in Appendix A (Appendix A.3,

Table A9. Overview of the selected model evaluation studies analyzed in this review. The type of evaluation (Ev.) is classified into calibration (CAL.) and validation (VAL.). The country code (Coun.) is reported together with the Köppen climate classification (K. C.) of the field trial site. The crop or the crop rotation (Crop) for which each treatment was tested are reported: potatoes, winter wheat, white cabbage, winter barley, grass-clover ley (rotation 1); rice, pepper, Chinese cabbage, white radish, cowpea (rotation 2); tomato, lettuce, cabbage, packchoi (rotation 3); corn, soybean, winter wheat (rotation 4); corn, soybean, and alfalfa (rotation 5). The tested treatment (Tr.) reviewed are the following: zero N control (N₀), mineral N fertilization (N_min), organic N fertilization (N_org), sandy–loam soil (SL), sandy–clay–loam soil (SCL), clay–loam soil (CL), crop management (Crop_mng), and soil moisture conditions (SWC). Averaged values of the fitting indices, referring to several tested treatments, are also reported (Overall) if published in the original evaluation study. The progressive number within each reference (Ref.) and type of evaluation combination of the tested treatments (n°) are also reported. The type of measure (Meas.) is classified into continuous measure (C) and not-continuous measure (N), while the value employed for N₂O emissions fitting (Fit.) is classified as daily value (d) and as cumulated value (c). The following evaluation metrics are reported: Pearson’s correlation coefficient (r), coefficient of determination (R²), root mean squared error (RMSE, kg N-N₂O ha⁻¹), RMSE at the 95% confidence level (RMSE₉₅, kg N-N₂O ha⁻¹), modeling efficiency (EF), relative root mean squared error (RRMSE, %), R² significance level (p-value).

Model	Ref.	Ev.	Coun.	K. C.	Crop	Meas.	Fit.	n°	Tr.	r	R2	RMSE	RMSE95	EF	RRMSE	p-Value
APSIM	[16]	CAL.	CHN	Cfb	corn	C	d	2	Nmin	-	0.31	-	-	-	-	-
	[16]	CAL.	CHN	Cfb	corn	C	d	2	Nmin	-	0.52	-	-	-	-	-
	[16]	CAL.	CHN	Cfb	corn	C	d	2	Nmin	-	0.56	-	-	-	-	-
	[16]	CAL.	CHN	Cfb	corn	C	c	2	Nmin	-	0.3	-	-	-	-	-
	[16]	CAL.	CHN	Cfb	corn	C	c	2	Nmin	-	0.67	-	-	-	-	-
	[16]	CAL.	CHN	Cfb	corn	C	c	2	Nmin	-	0.5	-	-	-	-	-
	[16]	VAL.	CHN	Cfb	winter wheat–corn	C	c	-	Overall	-	0.74	0.71	-	-	-	-
	[16]	VAL.	CHN	Cfb	winter wheat–corn	C	c	-	Overall	-	0.76	0.63	-	-	-	-
	[16]	VAL.	CHN	Cfb	winter wheat–corn	C	d	1	N0	-	0.05	0.01	-	-	-	-
	[16]	VAL.	CHN	Cfb	winter wheat–corn	C	d	2	Nmin	-	-	-	-	-	-	-
	[16]	VAL.	CHN	Cfb	winter wheat–corn	C	d	3	Nmin	-	0.38	0.03	-	-	-	-
	[16]	VAL.	CHN	Cfb	winter wheat–corn	C	d	4	Norg + Nmin	-	0.4	0.03	-	-	-	-
	[16]	VAL.	CHN	Cfb	winter wheat–corn	C	d	1	N0	-	0.08	0.01	-	-	-	-
	[16]	VAL.	CHN	Cfb	winter wheat–corn	C	d	2	Nmin	-	-	-	-	-	-	-
	[16]	VAL.	CHN	Cfb	winter wheat–corn	C	d	3	Nmin	-	0.45	0.03	-	-	-	-
	[16]	VAL.	CHN	Cfb	winter wheat–corn	C	d	4	Norg + Nmin	-	0.47	0.02	-	-	-	-
CERES-EGC	[90]	VAL.	IT	Csa	faba beans	C	d	1	Norg		0.74	0.002	2.09 × 10−3		-
	[89]	VAL.	SW	Cfb	sugar beet–winter wheat	N	d	1	N0		0.37	0.006	6.18 × 10−3	-	-	-
CoupModel	[7]	CAL.	SE	Cfb	red clover–winter wheat	N	c	1–16	Nmin + SWC	-	0.96	0.82	-	-	275	-
	[7]	CAL.	SE	Cfb	red clover–winter wheat	N	c	16	Overall	-	0.47	0.71	-	-	278	-
	[91]	VAL.	DE	Cfb	rapeseed	N	d	1	N0	-	0.26	0.04	-	-	-	-
	[91]	VAL.	DE	Cfb	rapeseed	N	d	2	Nmin	-	0.18	0.04	-	-	-	-
	[91]	VAL.	DE	Cfb	rapeseed	N	d	3	Nmin	-	0.5	0.05	-	-	-	-
DAYCENT	[11]	VAL.	USA	Bsk	grassland	N	c	1	SL		0.35	-	-	-	-	0.045
	[11]	VAL.	USA	Bsk	grassland	N	c	3	SCL	-	0.18	-	-	-	-	0.19
	[11]	VAL.	USA	Bsk	grassland	N	c	2	Nmin + SL	-	0.46	-	-	-	-	0.16
	[11]	VAL.	USA	Bsk	grassland	N	c	5	CL	-	0.64	-	-	-	-	0.01
	[11]	VAL.	USA	Bsk	grassland	N	c	-	Overall	-	0.26	-	-	-	-	0.0001
	[93]	VAL.	USA	Bsk	corn	N	c	1	Overall	-	0.29	-	-	-	-	-
	[92]	VAL.	CH	Cfb	rotation 1	N	c	1	Overall	-	0.89	1.04	-	-	25	-
	[11]	VAL.	USA	Bsk	grassland	N	c	4	Nmin + SCL	-	0.02	-	-	-	-	0.69
	[11]	VAL.	USA	Bsk	grassland	N	d	1	SL		0.07	-	-	-	-	0.0001
	[11]	VAL.	USA	Bsk	grassland	N	d	3	SCL	-	0.08	-	-	-	-	0.0006
	[11]	VAL.	USA	Bsk	grassland	N	d	2	Nmin + SL	-	0.19	-	-	-	-	0.0001
	[11]	VAL.	USA	Bsk	grassland	N	d	5	CL	-	0.02	-	-	-	-	0.1
	[11]	VAL.	USA	Bsk	grassland	N	d	-	Overall	-	0.09	-	-	-	-	0.0001
	[11]	VAL.	USA	Bsk	grassland	N	d	4	Nmin + SCL	-	0.02	-	-	-	-	0.14
DNDC v.9.5	[95]	VAL.	CHN	Cfa	rotation 3	C	c	-	Overall	-	0.95	-	-	-	-	-
	[94]	CAL.	CHN	Cfa	rotation 2	N	c	4	Overall	-	0.75	0.51	-	-	-	-
	[95]	VAL.	CHN	Cfa	rotation 3	C	d	1	Norg + Nmin	-	0.4	-	-	-	-	-
	[95]	VAL.	CHN	Cfa	rotation 3	C	d	2	Norg + Nmin	-	0.28	-	-	-	-	-
	[94]	CAL.	CHN	Cfa	rotation 2	N	d	1 + 2	Cropmng (rice)	-	-	0.01–0.03	-	-	-	-
	[94]	CAL.	CHN	Cfa	rotation 2	N	d	3 + 4	Cropmng (vegetable)	-	-	0.11	-	-	-	-
	[95]	VAL.	CHN	Cfa	rotation 3	C	d	3	Norg + Nmin + nitr. inhibitor	-	0.3	-	-	-	-	-
EPIC	[96]	VAL.	USA	Dfa	rotation 5	N	c	1–7	(4) Nmin + (3) Cropmng	-	0.54	1.32	-	-	-	-
	[82]	CAL.	USA	Dfa	rotation 4	N	c	-	Overall (2007)	-	0.88	0.67	-	-	-	-
	[82]	CAL.	USA	Dfa	rotation 4	N	c	-	Overall (2008)	-	0.78	0.39	-	-	-	-
	[96]	CAL.	USA	Dfa	rotation 5	N	c	1–7	(4) Nmin + (3) Cropmng	-	0.41	1.25	-	-	-	-
	[82]	CAL.	USA	Dfa	rotation 4	N	d	1	N0 (2007)	-	0.31	-	-	-	-	-
	[82]	CAL.	USA	Dfa	rotation 4	N	d	2	Nmin (2007)	-	0.63	-	-	-	-	-
	[82]	CAL.	USA	Dfa	rotation 4	N	d	3	Nmin (2007)	-	0.82	-	-	-	-	-
EPIC	[82]	CAL.	USA	Dfa	rotation 4	N	d	4	Nmin (2007)	-	0.78	-	-	-	-	-
	[82]	CAL.	USA	Dfa	rotation 4	N	d	5	Nmin (2007)	-	0.58	-	-	-	-	-
	[82]	CAL.	USA	Dfa	rotation 4	N	d	6	Nmin (2007)	-	0.7	-	-	-	-	-
	[82]	CAL.	USA	Dfa	rotation 4	N	d	-	Overall (2007)	-	0.92	0	-	-	-	-
	[82]	CAL.	USA	Dfa	rotation 4	N	d	1	N0 (2008)	-	0.1	-	-	-	-	-
	[82]	CAL.	USA	Dfa	rotation 4	N	d	2	Nmin (2008)	-	0.32	-	-	-	-	-
	[82]	CAL.	USA	Dfa	rotation 4	N	d	3	Nmin (2008)	-	0.55	-	-	-	-	-
	[82]	CAL.	USA	Dfa	rotation 4	N	d	4	Nmin (2008)	-	0.77	-	-	-	-	-
	[82]	CAL.	USA	Dfa	rotation 4	N	d	5	Nmin (2008)	-	0.64	-	-	-	-	-
	[82]	CAL.	USA	Dfa	rotation 4	N	d	6	Nmin (2008)	-	0.75		-	-	-	-
	[82]	CAL.	USA	Dfa	rotation 4	N	d	-	Overall (2008)	-	0.78	0.04	-	-	-	-
	[96]	CAL.	USA	Dfa	rotation 5	N	d	1–7	(4) Nmin + (3) Cropmng	-	0.45	0.01	-	-	-	-
	[96]	VAL.	USA	Dfa	rotation 5	N	d	1–7	(4) Nmin + (3) Cropmng	-	0.14	0.02	-	-	-	-
SPACSYS	[98]	VAL.	U.K.	Cfb	permanent pasture	C	d	1	Nmin	0.49	0.74	0.07	-	−0.2	-	-
	[71]	VAL.	GB–SCT	Cfb	grassland	N	c	1	N0	0.06	-	0.494	0.87	−22.25	-	-
	[71]	VAL.	GB–SCT	Cfb	grassland	N	c	3	Norg	0.5	-	0.177	0.747	0.2	-	-
	[71]	VAL.	GB–SCT	Cfb	grassland	N	c	2	Nmin	0.34	-	0.52	0.736	0.04	-	-
	[97]	VAL.	U.K.	Cfb	grassland	N	c	1	Nmin	0.98	-	0.1305	0.17415	-	-	-
	[97]	CAL.	U.K.	Cfb	grassland	N	c	1	Nmin	0.88	-	0.3841	0.24733	-	-	-
STICS	[99]	VAL.	SP, SP–C, FR	Cfa (SP), Csa (SP-C), Cfb (FR)	Durum wheat –faba bean	C	c	12	Nmin + Cropmng	-	0.4	-	-	0.24	45.6

).

3. Results

These sections report the main approaches for nitrous oxide simulation, with a major focus on process-based models. The other concurrent alternative approaches for the prediction and estimate of soil N₂O releases—such as IPCC approaches, statistical models, meta-models, and whole farm models—are reported in the Supplementary Material.

3.1. Process-Based Models

All the processes described are simulated for selected discrete soil layers at each time step unless otherwise specified. All the state and auxiliary variable values employed in the formulas correspond to the current time step value unless otherwise specified. In the following paragraphs, parameters are presented with their definition, symbol, unit of measure, and default value (when available). In this review, all variables and parameters are associated with a common symbol for all the models. The model-specific original symbols of variables (Appendix A.3,

Table A1. Nitrification module variables, unit of measures, original model symbols (original symbol), and symbols used in the present review (review symbol).

Model	Variable	Unit	Original Symbol	Review Symbol
APSIM	nitrification rate	mg N g−1 d−1	Rnit	Rnit
ARMOSA	nitrification rate	kg N ha−1 d−1	Nit_NH4	Rnit
ARMOSA	nitrate amount	kg N ha−1	NO3	NO3
ARMOSA	ammonium amount	kg N ha−1	NH4	NH4
CERES-EGC	nitrification rate	kg N ha−1 d−1	Ni	Rnit
CoupModel	nitrification rate	g N m−2 d−1	NNH4→NO3	Rnit
CoupModel	nitrifier biomass	g m−2	NmicrN	Bnit
CROPSYST	nitrification rate	kg N ha−1 d−1	NNH4→NO3	Rnit
CROPSYST	ammonium amount	kg N ha−1	NNH4	NH4
CROPSYST	nitrate amount	kg N ha−1	NNO3	NO3
DAYCENT	nitrification rate	g N m−2 d−1	FNO3	Rnit
DAYCENT	mineralization rate	g N m−2	Netmm	Netmm
DAYCENT	ammonium amount	g N m−2	NH4	NH4
DNDC	nitrification rate	kg N ha−1 d−1	RN	Rnit
DNDC	ammonium amount	kg N ha−1	[NH4+]	NH4
DNDC	nitrifier biomass	kg C ha−1	Nitrifier	Bnit
DSSAT	nitrification rate	kg N ha−1 d−1	NITRIF	Rnit
DSSAT	ammonium amount	kg N ha−1	NH4	NH4
EPIC	nitrification rate	kg N ha−1 d−1	RNIT	Rnit
EPIC	volatilization rate	kg N ha−1 d−1	AVOL	Rvol
EPIC	ammonium amount	kg N ha−1	NH3	NH4
EPIC	auxiliary variable	unitless	AKAV	AKAV
EPIC	soil temperature	°C	STMP	T
SPACSYS	nitrification rate (microbial explicit)	g N m−2 d−1	nn	Rnit
SPACSYS	water-filled pore space	unitless	WFPS	WFPS
SPACSYS	nitrifier biomass	g C m−2	Mb	Bnit
SPACSYS	nitrification rate	g N m−2 d−1	Nnitri	Rnit
STICS	nitrification rate (layer)	kg N ha−1 cm−1 d−1	TNITRIF	Rnit
STICS	nitrification rate (total)	kg N ha−1 d−1	NITRIF	Rnit(total)
STICS	ammonium amount	kg N ha−1	AMM	NH4
all model	nitrification response function to soil temperature	unitless	various	fn(T)
all model	nitrification response function to soil moisture	unitless	various	fn(W)
all model	nitrification response function to soil acidity	unitless	various	fn(pH)
all model	nitrification response function to ammonium level	unitless	various	fn(NH4)

,

Table A3. Denitrification module variables, unit of measures, original model symbols (original symbol), and symbols used in the present review (review symbol).

Model	Variable	Unit	Original Symbol	Review Symbol
APSIM	denitrification rate	kg N ha−1 d−1	Rdenit	Rdenit
APSIM	nitrate amount	kg N ha−1	NO3	NO3
APSIM	active C concentration	ppm	CA	[CA]
ARMOSA	denitrification rate	kg N ha−1 d−1	Denit_NO3	Rdenit
ARMOSA	nitrate concentration	kg N L−1	Conc_NO3	[NO3]
CERES-EGC	denitrification rate	kg N ha−1 d−1	PDR	Rdenit
CoupModel	denitrification rate	g N m−2 d−1	NNO3→Denit	Rdenit
CoupModel	NxOy consumption rate	g N m−2 d−1	NNxOy→AnNxOy	NNxOy→AnNxOy
CoupModel	NxOy content in the anaerobic pool	g N m−2 d−1	AnNxOy	AnNxOy
CoupModel	dpot depth-adjustment coefficient	unitless	ddist	zadj
CROPSYST	denitrification rate	kg N ha−1 d−1	Da	Rdenit
DAYCENT	denitrification rate	µg N g soil−1 d−1	Dt	Rdenit
DNDC	NxOy consumption rate	kg N ha−1 d−1	dNOx/dt	Rc,NxOy
DNDC	denitrifier biomass	kg N ha−1	Denitrifier	Bdenit
DSSAT	denitrification rate	kg N ha−1 d−1	DENITRIF	Rdenit
DSSAT	volumetric soil water content	m3 m−3	SW	SWC
DSSAT	drained upper limit	m3 m−3	DUL	DUL
DSSAT	soil temperature	K	ST	T
DSSAT	water-extractable soil C	kg C ha−1	CW	CW
DSSAT	nitrate amount	kg N ha−1	NO3	NO3
EPIC	denitrification rate	kg N ha−1 d−1	DN	Rdenit
EPIC	soil weight	kg	WT	WT
EPIC	nitrate amount	kg N ha−1	NO3	NO3
SPACSYS	NxOy consumption rate	kg N m−3 d−1	dc,i	Rc,NxOy
SPACSYS	NxOy concentration	kg N m−3	Ni	[NxOy]
SPACSYS	total NxOy concentration	kg N m−3	Ntotal	∑[NxOy]
SPACSYS	denitrification rate	g N m−2 d−1	Ndeni	Rdenit
STICS	denitrification rate (total)	kg N ha−1 d−1	NDENENG	Rdenit
all model	denitrification response function to soil temperature	unitless	various	fd(T)
all model	denitrification response function to soil moisture	unitless	various	fd(W)
all model	denitrification response function to soil acidity	unitless	various	fd(pH)
all model	denitrification response function to NxOy level	unitless/µg N g soil−1 d−1	various	fd(NxOy)
all model	denitrification response function to DOC level	unitless	various	fd(DOC)
all model	denitrification response function to heterotrophic respiration	unitless/µg N g soil−1 d−1	various	fd(CO2)

,

Table A5. Emissions module variables, unit of measures, original model symbols (original symbol), and symbols used in the present review (review symbol).

Model	Variable	Unit	Original Symbol	Review Symbol
APSIM	nitrification N2O emission rate	kg N ha−1 d−1	N2Onit	N2Onit
APSIM	denitrification N2O emission rate	kg N ha−1 d−1	N2Odenit	N2Odenit
APSIM	nitrate concentration	µg N g−1	NO3ppm	[NO3]
APSIM	heterotrophic respiration rate	µg C g soil−1 d−1	CO2	CO2,resp
ARMOSA	nitrification N2O emission rate	kg N ha−1 d−1	Nit_N2O	N2Onit
ARMOSA	denitrification N2O emission rate	kg N ha−1 d−1	Denit_N2O	N2Odenit
ARMOSA	nitrate amount	kg N ha−1	NO3	NO3
ARMOSA	heterotrophic respiration rate	kg C ha−1 d−1	CO2	CO2,resp
ARMOSA	soil water content at saturation	m3 m−3	SWCsat	SWCsat
CoupModel	nitrification NO emission rate	g N m−2 d−1	NOnit	NOnit
CoupModel	emissions response function to soil temperature	unitless	fe(T)	fe(T)
CoupModel	emissions response function to soil moisture	unitless	fe(W)	fe(W)
CoupModel	emissions response function to soil acidity	unitless	fe(pH)	fe(pH)
CoupModel	nitrification N2O emission rate	g N m−2 d−1	N2Onit	N2Onit
CROPSYST	denitrification N2O emission rate	µg N kg−1 d−1	DN2O	N2Odenit
CROPSYST	N2/N2O ratio	unitless	RN2/N2O	RN2/N2O
CROPSYST	denitrification N2 emission rate	µg N kg−1 d−1	DN2	N2,denit
CROPSYST	emissions response function to nitrate level	unitless	fr(NO3)	fe(NO3)
CROPSYST	emissions response function to heterotrophic respiration	unitless	fr(CO2)	fe(CO2)
CROPSYST	emissions response function to soil moisture	unitless	fr(W)	fe(W)
DAYCENT	denitrification N2O emission rate	g N m−2 d−1	N2Odenit	N2Odenit
DAYCENT	N2/N2O ratio	unitless	RN2/N2O	RN2/N2O
DAYCENT	DFC function	unitless	Fr(NO3/CO2)	fe(NO3/CO2)
DAYCENT	N2/N2O ratio response function to soil moisture	unitless	Fr(WFPS)	fe(W)
DAYCENT	nitrification N2O emission rate	g N m−2 d−1	N2Onit	N2Onit
DAYCENT	NOx emission rate	g N m−2 d−1	NOx	NOx,nit+denit
DAYCENT	NOx/N2O ratio	unitless	RNOx	RNOx/N2O
DAYCENT	pulse multiplier	unitless	P	P
DNDC	nitrification N2O emission rate	kg N ha−1 d−1	N2ON	N2Onit
DNDC	denitrification N2O emitted fraction	unitless	P(N2O)	P(N2O)
DNDC	denitrification N2 emitted fraction	unitless	P(N2)	P(N2)
DSSAT	nitrification N2O emission rate	kg N ha−1 d−1	N2Onit	N2Onit
DSSAT	nitrification NO emission rate	kg N ha−1 d−1	NOnit	NOnit
DSSAT	NO/N2O ratio	unitless	NO_N2O_ratio	RNOx/N2O
DSSAT	pulse multiplier	unitless	P	P
DSSAT	denitrification N2O emission rate	kg N ha−1 d−1	N2Odenit	N2Odenit
DSSAT	denitrification N2 emission rate	kg N ha−1 d−1	N2	N2,denit
DSSAT	N2/N2O ratio	unitless	Rn2n2o	RN2/N2O
DSSAT	auxiliary variable	unitless	ratio1	ratio1
DSSAT	auxiliary variable	unitless	ratio2	ratio2
DSSAT	emissions response function to nitrate level	unitless	fe(NO3)	fe(NO3)
DSSAT	emissions response function to soil moisture	unitless	fe(W)	fe(W)
DSSAT	water-filled pore space	unitless	WFPS	WFPS
EPIC	denitrification N2O emission rate	kg N ha−1 d−1	DN2O	N2Odenit
EPIC	denitrification N2 emission rate	kg N ha−1 d−1	DN2	N2,denit
SPACSYS	denitrification N2O emitted fraction	unitless	P(N2O)	P(N2O)
SPACSYS	denitrification N2 emitted fraction	unitless	P(N2)	P(N2)
SPACSYS	adsorption factor	unitless	AD	fe(AD)
SPACSYS	total porosity air-filled fraction	unitless	AP	1-WFPS
SPACSYS	nitrification N2O emission rate	ng N g soil−1 d−1	N2O	N2Onit
SPACSYS	soil temperature	°C	T	T
STICS	nitrification N2O emission rate	kg N ha−1 d−1	N2Onit	N2Onit
STICS	denitrification N2O emission rate	kg N ha−1 d−1	N2Odenit	N2Odenit

and

Table A7. Parameters of the environmental response functions of nitrification (nit.), denitrification (denit.), and emissions (emiss.): unit of measures, original model symbols (original symbol), and symbols used in the present review (review symbol), default values [range].

Function	Model	Parameter	Unit	Original Symbol	Review Symbol	Default
f(T)	ARMOSA	response to a 10 °C T change	unitless	Q10	tQ10	2 [1.5–4.0]
f(T)	ARMOSA	base T for the microbial activity	°C	Tbase	Topt	20
f(T)	CERES-EGC	nit. response to a 10 °C T change	unitless	Q10nit	tQ10	2.1
f(T)	CERES-EGC	denit. threshold T	°C	TTrdenit	Tdenit	11
f(T)	CERES-EGC	denit. response to a 10 °C T change	unitless	Q10denit,1	tQ10,1	89
f(T)	CERES-EGC	denit. response to a 10 °C T change	unitless	Q10denit,2	tQ10,2	2.1
f(T)	CoupModel	nit./denit. cardinal Tmin	°C	tmin	Tmin	−8
f(T)	CoupModel	nit./denit. cardinal Tmax	°C	tmax	Tmax	20
f(T)	CoupModel	base T for microbial activity	°C	tQ10base	Topt	20
f(T)	CoupModel	Q10 threshold	°C	tQ10thres	TQ10thres	5
f(T)	CoupModel	response to a 10 °C T change	unitless	tQ10	tQ10	2
f(T)	CoupModel	emissions Tmax	°C	gTmaxNxO	gTmaxNxO	33.5
f(T)	CoupModel	emissions Topt	°C	gToptNxO	gToptNxO	23.5
f(T)	CoupModel	response function shape coefficient	unitless	gTshapeNxO	gTshapeNxO	1.5
f(T)	CROPSYST	nitrification cardinal Topt	°C	TEMBAS	Topt,nit	20
f(T)	CROPSYST	response to a 10 °C T change	unitless	TEMQ10	tQ10	3 [1.5–4.0]
f(T)	DNDC	denitrification cardinal Tmax	°C	60	Tmax,denit	60
f(T)	STICS	nitrification cardinal Tmin	°C	TNITMING	Tmin,nit	5
f(T)	STICS	nitrification cardinal Topt	°C	TNITOPTG	Topt,nit	20
f(T)	STICS	nitrification cardinal Tmax	°C	TNITMAXG	Tmax,nit	45
f(T)	STICS	denitrification cardinal T1	°C	TDENREF1G	T1,denit	11
f(T)	STICS	denitrification cardinal T2	°C	TDENREF2G	T2,denit	20
f(W)	APSIM	SWC at which denitrification ceases	m3 m−3	SWClim	SWClim	-
f(W)	APSIM	empirical coefficient	unitless	X	x	1 [0.9–5.0]
f(W)	ARMOSA	empirical coefficient	unitless	denitWC	x	1 [0.9–5.0]
f(W)	ARMOSA	microbial activity below SWCmin	unitless	fmin	fmin	0
f(W)	ARMOSA	microbial activity above SWCmax	unitless	fmax	fmax	0.5
f(W)	ARMOSA	response function shape coefficient	unitless	A	a	1
f(W)	ARMOSA	response function shape coefficient	unitless	B	b	1
f(W)	ARMOSA	saturation threshold	unitless	thrsat	thrsat	0.6
f(W)	ARMOSA	lower threshold	unitless	thrdenit	thrdenit	0.05
f(W)	CERES-EGC	minimum WFPS for nitrification	%	MINWFPS	WFPSmin,nit	0.1
f(W)	CERES-EGC	optimum WFPS for nitrification	%	OPTWFPS	WFPSopt,nit	0.6
f(W)	CERES-EGC	maximum WFPS for nitrification	%	MAXWFPS	WFPSmax,nit	0.8
f(W)	CERES-EGC	threshold WFPS for denitrification	%	TrWFPS	WFPSdenit	0.62
f(W)	CERES-EGC	denit. response function exponent	unitless	POWdenit	x	1.74
f(W)	CoupModel	SWC effect on denit. coefficient	unitless	pθDp	pθDp	10
f(W)	CoupModel	SWC range from saturation	%	pθDRange	pθDRange	10
f(W)	CoupModel	saturation activity	unitless	pθsatact	pθsatact	0.6 [0–1]
f(W)	CoupModel	water content interval lower limit	%	pθLow	pθLow	13 [8–15]
f(W)	CoupModel	function shape coefficient	unitless	pθp	pθp	1
f(W)	CoupModel	water content interval upper limit	%	pθUpp	pθUpp	8 [1–10]
f(W)	CoupModel	relative saturation level	unitless	gθsatcrit	gθsatcrit	Table A8
f(W)	CoupModel	function shape coefficient	unitless	gθsatform	gθsatform	Table A8
f(W)	CROPSYST	saturation activity	unitless	MOSSA	pθsatact	0.6 [0–1]
f(W)	CROPSYST	function shape coefficient	unitless	MOSM	pθp	1
f(W)	CROPSYST	water content interval lower limit	%	MOS(1)	pθLow	13 [8–15]
f(W)	CROPSYST	water content interval upper limit	%	MOS(2)	pθUpp	8 [1–10]
f(W)	SPACSYS	soil bulk density	g cm−3	ρd	BD	-
f(W)	SPACSYS	soil particle density	g cm−3	ρs	PD	-
f(W)	STICS	optimal SWC for nitrification	unitless	HOPTNG	SWCopt,nit	1.0
f(W)	STICS	minimum SWC for nitrification	unitless	HIMINNG	SWCmin,nit	0.67
f(W)	STICS	reference T for mineralization	°C	TREFG	Tminer	15
f(W)	STICS	soil bulk density	g cm−3	DA	BD	-
f(pH)	APSIM	nitrification pH minimum threshold	unitless	-	pHmin	4.5
f(pH)	APSIM	nit. pH optimum minimum value	unitless	-	pHoptmin	6
f(pH)	APSIM	nit. pH optimum maximum value	unitless	-	pHoptmax	8
f(pH)	APSIM	nitrification pH maximum threshold	unitless	-	pHmax	9
f(pH)	ARMOSA	nitrification pH minimum threshold	unitless	PHMIN	pHmin	3
f(pH)	ARMOSA	nitrification pH maximum threshold	unitless	PHMAX	pHmax	5.5
f(pH)	CoupModel	pH half rate	unitless	dpHrate	dpHrate	4.25
f(pH)	CoupModel	shape coefficient	unitless	dpHshape	dpHshape	0.5
f(pH)	CoupModel	nitrification pH minimum threshold	unitless	gpHcoeff	pHmin	4.7
f(pH)	CROPSYST	nitrification pH minimum threshold	unitless	PHMIN	pHmin	-
f(pH)	CROPSYST	nitrification pH maximum threshold	unitless	PHMAX	pHmax	-
f(pH)	DAYCENT	parameter of arctan function	unitless	A	a	-
f(pH)	DSSAT	nitrification pH minimum threshold	unitless	-	pHmin	-
f(pH)	DSSAT	nitrification pH optimum threshold	unitless	-	pHopt	-
f(pH)	EPIC	nit. pH optimum minimum value	unitless	-	pHoptmin	7
f(pH)	EPIC	nit. pH optimum maximum value	unitless	-	pHoptmax	7.4
f(pH)	STICS	nitrification pH minimum threshold	unitless	PHMINNITG	pHmin	3
f(pH)	STICS	nitrification pH maximum threshold	unitless	PHMAXNITG	pHmax	5.5
f(S)	CERES-EGC	nit. half-saturation constant	mg N kg−1	Kmnit	Km,nit	10
f(S)	CERES-EGC	denit. half-saturation constant	mg N kg−1	Kmdenit	Km,denit	22
f(S)	CoupModel	half-saturation constant	mg N L−1	dNhalfsat	Km	10 [5–15]
f(S)	CoupModel	layer thickness	m	∆z	zlayer	-
f(S)	CoupModel	NO3:NH4 ratio	unitless	rnitr,amm	rNO3/NH4	8 [1–15]
f(S)	CoupModel	nit. coefficient	d−1	nrate	knit	0.2
f(S)	CoupModel	nit. half-saturation constant	mg N L−1	nhrateNH	Km	6.18
f(S)	DSSAT	minimum nitrate amount	kg N ha−1 d−1	min_nitrate	NO3,min	0.1
f(S)	SPACSYS	half-saturation constant	g C m−3 or g N m−3	km	Km	[9.45–18.53]

) and parameters (Appendix A.3,

Table A2. Nitrification module parameters, unit of measure, original model symbol, and symbol used in the present review, default values [range].

Model	Parameter	Unit	Original Symbol	Review Symbol	Default
APSIM	nitrification coefficient	mg N g−1 d−1	Vmax	Vmax	40
APSIM	nitrification half-saturation constant	mg N g−1	Km	Km	90
ARMOSA	nitrification coefficient	d−1	kn	knit	0.2
ARMOSA	NO3:NH4 ratio	unitless	Nratio	rNO3/NH4	8 [1–15]
CERES-EGC	nitrification coefficient	kg N ha−1 d−1	MNR	knit	-
CoupModel	pH response function coefficient	unitless	npH	kpH	1
CoupModel	nitrification coefficient	mg ha d−1 kg−1	nmicrate	knit	0.25
CROPSYST	nitrification coefficient	d−1	NITK	knit	0.2
CROPSYST	NO3:NH4 ratio	unitless	NITR	rNO3/NH4	8 [1–15]
DAYCENT	nitrified fraction of Netmm	d−1	K1	knit2	0.2
DAYCENT	nitrified fraction of NH4+	d−1	Kmax	knit	0.1
DNDC	nitrification coefficient	d−1	0.005	knit	0.005
EPIC	nitrified/volatilized fraction of NH3	unitless	PARAM(64)	knit3	[0–1]
SPACSYS	nitrification coefficient (microbial explicit)	d−1	nnmax	knit	0.004
SPACSYS	nitrification coefficient	d−1	knitri	knit	-
STICS	max depth for nitrification	cm	PROFHUMS	znit	30
STICS	nitrification coefficient	d−1	FNXG	knit	0.5
STICS	N2O:total nitrification ratio	unitless	RATIONITS	rN2O/nit	-

,

Table A4. Denitrification module parameters, unit of measure, original model symbol, and symbol used in the present review, default values [range].

Model	Parameter	Unit	Original Symbol	Review Symbol	Default
APSIM	denitrification coefficient	Unitless	kdenit	kdenit	0.0006
ARMOSA	denitrification coefficient	kg N ha−1 d−1	kd	kdenit	[0.04–0.2]
ARMOSA	denitrification half-saturation constant	mg N L−1	Hsconst	Km	[5–15]
CERES-EGC	denitrification coefficient	kg N ha−1 d−1	PDR	kdenit	-
CoupModel	denitrification coefficient	g N m−2 d−1	dpot	kdenit	0.04
CROPSYST	denitrification coefficient	kg N ha−1 d−1	Dp	kdenit	-
DNDC	growth yield on NxOy	kg C kg N−1	YNOx	YNxOy	-
DNDC	maintenance coefficient on NxOy	kg N kg−1 h−1	MNOx	MNxOy	-
DSSAT	max depth for denitrification	m	Denit_depth	zdenit	0.3
DSSAT	denitrification coefficient	d−1	0.0006	kdenit	0.0006
EPIC	denitrification coefficient	Unitless	DNITMX	kdenit	32
SPACSYS	denitrification coefficient	g N m−2 d−1	kdeni	kdenit	-
SPACSYS	maintenance coefficient on NxOy	g C g N−1 d−1	MNi	MNxOy	Table A8
SPACSYS	growth yield on NxOy	g C g N−1	YNi	YNxOy	Table A8
SPACSYS	growth rate on NxOy	d−1	γgd	γgd	Table A8
STICS	denitrification coefficient	kg N ha−1 d−1	VPOTDENITS	kdenit	16
STICS	max depth for denitrification	cm	PROFDENITS	zdenit	20

,

Table A6. Emissions module parameters, unit of measure, original model symbols (original symbol), and symbols used in the present review (review symbol), default values [range].

Model	Parameter	Unit	Original Symbol	Review Symbol	Default
APSIM	N2O emission: total nitrification ratio	unitless	k2	rN2O/nit	0.002
APSIM	gas diffusivity	unitless	k1	gdiff	25.1
ARMOSA	N2O emission: total nitrification ratio	unitless	fN2O	rN2O/nit	0.002
ARMOSA	gas diffusivity	unitless	diffd	gdiff	25.1
CERES-EGC	N2O emission: total nitrification ratio	unitless	C	rN2O/nit	-
CERES-EGC	N2O emission: total denitrification ratio	unitless	R	rN2O/denit	-
CoupModel	NO emission: total nitrification ratio	unitless	gmfracNO	rNO/nit	0.004
CoupModel	N2O emission: total nitrification ratio	unitless	gmfracN2O	rN2O/nit	0.0006
DAYCENT	gas diffusivity	unitless	DFC or D/D0	gdiff	-
DAYCENT	N2O emission: total nitrification ratio	unitless	K2	rN2O/nit	0.02
DNDC	N2O emission: total nitrification ratio	unitless	0.0024	rN2O/nit	0.0024
DSSAT	N2O emission: total nitrification ratio	unitless	0.001	rN2O/nit	0.001
DSSAT	gas diffusivity	unitless	DFC	gdiff	-
DSSAT	gas diffusivity	unitless	dD0	gdiff	-
EPIC	N2 emission: total denitrification	unitless	PARM(80)	rN2/denit	[0.1–0.9]
STICS	N2O emission: total nitrification ratio	unitless	RATIONITS	rN2O/nit	-
STICS	N2O emission: total denitrification ratio	unitless	RATIODENITS	rN2O/denit	-

and

Table A8. N_xO_y oxide-specific parameters default values.

Model	Module	Parameter	NO3− Value	NO2− Value	NO Value	N2O Value
CoupModel	emissions	gθsatcrit	-	-	0.45	0.55
CoupModel	emissions	gθsatform	-	-	0.024	0.24
CoupModel	microbial biomass	γd,NxOy	16	16	8.2	8.2
CoupModel	microbial biomass	deffNxOy	0.401	0.428	0.428	0.151
CoupModel	microbial biomass	drcNxOy	2.2	0.84	0.84	1.9
SPACSYS	microbial biomass	γgd	13.65	7.83	8.28	8.81
SPACSYS	denitrification	YNxOy	0.65	0.17	0.75	0.24
SPACSYS	denitrification	MNxOy	2.16	8.38	1.90	1.90

) are reported in Appendix A.

3.1.1. Nitrification

Approaches Based on Implicit Microbial Pools

In APSIM [67], the potential nitrification rate (R_nit, mg N g⁻¹ soil d⁻¹, Equation (1)) follows a Michaelis–Menten kinetics [72] and employs two parameters: the maximum reaction velocity (V_max, mg N g⁻¹ soil d⁻¹, 40), and the ammonium concentration ([NH₄]) to obtain half of V_max (K_m, mg N g⁻¹ soil, 90). The nitrification rate is obtained by limiting the potential rate with the response function to soil acidity, soil moisture, and temperature.

$$R_{nit}=\frac{V_{max}·\left[{NH}_4\right]}{K_m+\left[{NH}_4\right]}·\mathit{min}[f\left(T\right), f\left(W\right), f\left(pH\right)]$$

(1)

In the ARMOSA [56] and CROPSYST [69,73] models, the nitrification rate (R_nit, kg N ha⁻¹ d⁻¹, Equation (2)) is simulated using the SOILN approach [74,75]. A daily nitrification coefficient (k_nit, d⁻¹, 0.2) is employed, together with the nitrate–ammonium ratio for nitrification (r_NO3/NH4, unitless, 8, from 1 to 15 in agricultural soils). ARMOSA also employs a multiplicative aerobic factor (f_n(OX), unitless) that simulates the effect of tillage operations within 45 days of the first application. After this period, or if meanwhile 100 mm of rain has fallen, the factor is no longer considered in the rate estimate.

$$R_{nit}=k_{nit}·\left(\frac{N_{NH4}-N_{NO3}}{r_{NO3/NH4}}\right)·f_n(T)·f_n(W) ·f_n(pH)$$

(2)

In CERES-EGC [76], the nitrification rate (R_nit, kg N ha⁻¹ d⁻¹, Equation (3)) is obtained by limiting the maximum nitrification rate (k_nit, kg N ha⁻¹ d⁻¹), representing the site-specific nitrification rate at 20 °C, with three unitless response functions to soil ammonium concentration, water-filled pore space, and temperature.

$$R_{nit}=k_{nit}·f_n\left(T\right)·f_n\left(W\right)·f_n\left({NH}_4\right)$$

(3)

In CoupModel [68], the nitrification rate (R_nit, g N m⁻² d⁻¹, Equation (4)) can be estimated with a simplified approach or with an explicit microbial biomass approach (Equation (10)). In the simplified approach, the nitrification rate (R_nit, g N m⁻² d⁻¹) depends on a soil acidity coefficient (k_pH, unitless, 1), which is limited by the response functions to soil temperature, water-filled pore space, ammonium, and nitrate concentrations.

$$R_{nit}=f\left(T\right)·f_n\left(W\right)·f_n\left({NH}_4,{NO}_3\right)·k_{pH}$$

(4)

In DAYCENT [11] version 4.7, the nitrification rate (R_nit, g N m⁻² d⁻¹, Equation (5)) consists of a fraction of the daily net mineralization from the SOM submodel (Net_mm, g N m⁻²), which is assumed to be nitrified each day (K_nit2, d⁻¹, 0.2), and in a maximum nitrified fraction (K_nit, d⁻¹, 0.1) of the soil ammonium concentration (NH₄, g N m⁻²).

$$R_{nit}={Net}_{mm}·k_{nit2}+k_{nit}·{NH}_4·f_n\left(T\right)·f_n\left(W\right)·f_n\left(pH\right)$$

(5)

In DSSAT [70] V4.8.2.0 [77], the nitrification rate (R_nit, kg N ha⁻¹ d⁻¹, Equation (6)) is limited through response functions to soil temperature, moisture, and acidity, which range between 0 and 1, and it is further reduced in the presence of a nitrification inhibitor compound.

$$R_{nit}={NH}_4·\left[f_{n1}\left(T\right)·f_n\left(W\right)+f_n\left(pH\right)+f_{n2}\left(T\right)\right]$$

(6)

In EPIC [62] version 1102 [78], the nitrification rate (R_nit, kg N ha⁻¹ d⁻¹, Equation (7)) is simulated as depending on the ammonium availability, net of nitrogen volatilization (R_vol, kg N ha⁻¹ d⁻¹). The response function of nitrification to soil moisture is based on soil water content (f₁(W)), and it is also employed in the denitrification estimate. The auxiliary variable (AKAV, unitless) estimate depends on the considered layer: for the first layer, it depends on soil temperature and wind speed; for the deeper layers, it depends on temperature and a cationic exchange capacity factor. The parameter employed (k_nit3, unitless, between 0 and 1) represents the upper limit of nitrification—volatilization as a fraction of the present ammonium.

$$R_{nit}=min\left\{k_{nit3}, 1-e^{-\left[AKAV+\left(f_n\left(T\right)·f_1\left(W\right)·f_n\left(pH\right)\right)\right]}\right\}·{NH}_4-R_{vol}$$

(7)

In the SPACSYS model [66], the nitrification rate (R_nit, g N m⁻² d⁻¹, Equation (8)) in the implicit microbial biomass approach depends on the maximum rate of nitrification (k_nit, d⁻¹) parameters, which is limited by the response functions to soil temperature, water-filled pore space, and ammonium and nitrate concentration.

$$R_{nit}=k_{nit}·f\left(T\right)·f_n\left(W\right)·f_n\left({NH}_4,{NO}_3\right)$$

(8)

In STICS [60], nitrification occurs only in the biologically active soil layer, which is constrained by a maximum depth parameter (z_nit, cm, 30). The nitrification rate in each layer (R_nit, kg N ha⁻¹ cm⁻¹, Equation (9)) depends on the daily maximum fraction of ammonium converted in nitrate (k_nit, d⁻¹) and on the ratio between N₂O emissions and total nitrification (r_N2O/nit, unitless). The total nitrification is obtained as the sum of each layer’s nitrification rate above the maximum depth.

$$R_{nit}=\left(1-r_{N2O/nit}\right) {·k}_{nit}·{NH}_4·f_n\left(T\right)·f_n\left(W\right)·f_n\left(pH\right)$$

(9)

Approaches Based on Explicit Microbial Pools

In CoupModel [68], when nitrifying microbials are explicitly taken into account, the nitrification rate (R_nit, g N m⁻² d⁻¹, Equation (10)) is directly proportional to a rate coefficient (k_nit, mg ha d⁻¹ kg⁻¹, 0.25) and to the nitrifiers microbial biomass (B_nit, g m⁻²), limited by the response functions to environmental factors and to ammonium solute concentration.

$$R_{nit}=k_{nit}·f\left(T\right)·f_n\left(W\right)·f_n\left({NH}_4\right)·k_{pH}·B_{nit}$$

(10)

In DNDC model version 9.5 [79], the nitrification rate (R_nit, kg N ha⁻¹ d⁻¹, Equation (11)) is calculated on the base of a nitrification coefficient (k_nit, d⁻¹, 0.005), the ammonium amount (kg N ha⁻¹), the soil acidity (pH, unitless), and the nitrifiers biomass (B_nit, kg C ha⁻¹).

$$R_{nit}=k_{nit}·{NH}_4·B_{nit}·pH$$

(11)

For the explicit microbial pools approach of the SPACSYS model [71], the nitrification rate (R_nit, g N m⁻² d⁻¹, Equation (12)) depends on the nitrifier biomass (B_nit, g C m⁻²) and on the maximum rate of nitrification (k_nit, d⁻¹, 0.004) parameters, which is limited by the response functions to soil temperature, water-filled pore space, soil acidity, and ammonium concentration.

$$R_{nit}=k_{nit}·f\left(T\right)·f\left(W\right)·f_n\left(pH\right)·f_n\left({NH}_4\right)·B_{nit}$$

(12)

3.1.2. Denitrification

Approaches Based on Implicit Microbial Pools

In the APSIM model [67], the denitrification rate (R_denit, kg N ha⁻¹ d⁻¹, Equation (13)) is simulated as a fraction (k_denit, unitless, 0.0006) of the nitrate (kg N ha⁻¹) amount, limited by active carbon concentration ([C_A], ppm, Appendix A.2, Appendix A) and soil temperature moisture response functions.

$$R_{denit}=k_{denit}·{NO}_3·\left[C_A\right]·f_d\left(T\right)·f_d\left(W\right)$$

(13)

In ARMOSA [56], the denitrification rate (R_denit, kg N ha⁻¹ d⁻¹, Equation (14)) is simulated using SOILN approach [75]: a daily denitrification rate (k_denit, kg N ha⁻¹ d⁻¹, 0.04, between 0.04 and 0.2) is employed, together with a denitrification half-saturation constant (K_m, mg N L⁻¹, 10, between 5 and 15) defining the nitrate concentration ([NO₃], kg N L⁻¹) at which denitrification activity is half of the activity at optimum nitrate concentration.

$$R_{denit}=k_{denit}·\frac{\left[{NO}_3\right]}{\left[{NO}_3\right]+\frac{K_m}{{10}^6}}·f(T)·f_d(W)$$

(14)

In CERES-EGC [76], the denitrification rate (R_denit, kg N ha⁻¹ d⁻¹, Equation (15)) is obtained by limiting the potential rate (k_denit, kg N ha⁻¹ d⁻¹), representing the site-specific denitrification rate at 20 °C, with three unitless response functions to soil nitrate concentration, water-filled pore space, and temperature.

$$R_{denit}=k_{denit}·f_d\left(T\right)·f_d\left(W\right)·f_d\left({NO}_3\right)$$

(15)

In CoupModel [68], the denitrification rate (R_denit, g N m⁻² d⁻¹) is either not accounted for (denitrification not simulated), or it can be calculated with a simplified approach (where the rate depends on response functions for soil temperature, soil moisture, and nitrate concentration in the soil with denitrifying microorganisms not explicitly simulated, Equation (16)) or with an explicit denitrifying microorganisms biomass approach (Equation (25)). The denitrification rate, when simulated, can be differentiated through the soil profile: it can be evenly distributed (constant), or it can decrease linearly or exponentially with the depth of the soil layer (∆z). A factor (z_adj, unitless) adjusts the potential denitrification rate parameter (k_denit, g N m⁻² d⁻¹, 0.04) for each soil layer.

$$R_{denit}=k_{denit}·f\left(T\right)·f_d\left(W\right)·f_d\left({NO}_3\right)·z_{adj}(∆z)$$

(16)

In the CROPSYST model [59,69,73], the actual denitrification rate (R_denit, kg N ha⁻¹ d⁻¹, Equation (17)) is obtained by limiting a potential denitrification rate (k_denit, kg N ha⁻¹ d⁻¹) with environmental factors response functions [80] to soil nitrate, soil heterotrophic respiration, and water content.

$$R_{denit}=k_{denit}·min\left[f_d\left({NO}_3\right),f_d\left({CO}_2\right)\right]·f_d\left(W\right)$$

(17)

In DAYCENT model 4.7 [11], the total N flux (R_denit, µg N g soil⁻¹ d⁻¹, Equation (18)) from denitrification [81] is obtained using a response function to nitrate level (f_d(NO₃), µg N g soil⁻¹ d⁻¹) and a response function to heterotrophic respiration (f_d(CO₂), µg N g soil⁻¹ d⁻¹), which surrogates labile C availability, together with a response function to WFPS (f_d(W), unitless), which surrogates O₂ soil status.

$$R_{denit}=min\left[f_d\left({NO}_3\right),f_d\left({CO}_2\right)\right]·f_d\left(W\right)$$

(18)

In DSSAT model [70] V4.8.2.0 [77], the denitrification of NO₃ to N₂O and N₂ gases can be simulated using the DAYCENT or CERES denitrification subroutine. In the DAYCENT subroutine, the NO₃ denitrification rate (R_denit, kg N ha⁻¹ d⁻¹, Equation (19)) is derived from the DAYCENT model [81]. The denitrification rate is calculated for each soil layer and is accelerated for the soil layer whose depth (z, m) comprises 0 and the parameter z_denit (m, 0.3 default).

$$R_{denit}=\left\{\begin{array}{c}{f}_d\left(W\right)·\mathit{min}\left[f_d\left({NO}_3\right),f_d\left({CO}_2\right)\right] if z>z_{denit}\\ f_d\left(W\right)·max\left\{\mathit{min}\left[f_d\left({NO}_3\right),f_d\left({CO}_2\right)\right], 0.066\right\} if z<z_{denit}\end{array}\right.$$

(19)

In the CERES denitrification subroutine, denitrification only occurs when nitrate is present (NO₃ > 0.01 kg N ha⁻¹), the soil water content (SWC, m³ m⁻³) is higher than the drained upper limit (DUL, m³ m⁻³), and the soil temperature (T, K) is higher than 5. The denitrification rate (R_denit, kg N ha⁻¹ d⁻¹, Equation (20)) depends on a denitrification coefficient (k_denit, d⁻¹, 0.0006), water-extractable soil carbon (C_W), nitrate content, and water and temperature response functions.

$$R_{denit}=k_{denit}·{NO}_3·C_W·f_d\left(W\right)·f_d\left(T\right)$$

(20)

In EPIC model v. 1102 [62], three methods for the denitrification routine can be selected from the control file: IMWJ [82], Armen Kemanian denitrification method, and the original EPIC denitrification method [78]. The IMWJ (Izaurralde, McGill, Williams, and Jones) denitrification option (not reported) calculates the total number of electrons released by C oxidation and accepted by O₂ and oxides of N (NO₃⁻, NO₂⁻ and N₂O) during an hour for a given layer. The movement of N₂O through the soil profile and of N₂O and N₂ through the liquid phase are also simulated. In the Armen Kemanian denitrification method, the denitrification rate (R_denit, kg N ha⁻¹ d⁻¹, Equation (21)) is estimated by considering a parameter (k_denit, unitless, 32), the soil layer weight (WT), and the response functions to nitrate content, soil moisture, and respiration level.

$$R_{denit}=f_d\left({NO}_3\right)· f_d\left(W\right)·f_d\left({CO}_2\right)· k_{denit}·WT·{10}^{-3}$$

(21)

In the original EPIC denitrification method, the denitrification rate (R_denit, kg N ha⁻¹ d⁻¹, Equation (22)) employs a soil temperature factor, and two soil moisture factors (f₁(W), also employed in the nitrification subroutine, and f_d(W) also employed in Equation (21)).

$$R_{denit}={NO}_3·\sqrt{f_d\left(T\right)·f_1\left(W\right)}·f_d\left(W\right)$$

(22)

In the implicit microbial biomass approach of the SPACSYS model [66], the denitrification rate (R_denit, g N m⁻² d⁻¹, Equation (23)) depends on the maximum rate of denitrification (k_denit, g N m⁻² d⁻¹) parameter, which is limited by the response functions to soil temperature, water-filled pore space, and nitrate concentration.

$$R_{denit}=k_{denit}·f\left(T\right)·f_d\left(W\right)·f_d\left({NO}_3\right)$$

(23)

In the STICS model [60], the daily denitrification rate (R_denit, kg N ha⁻¹ d⁻¹, Equation (24)) is simulated with the approach of [83] only for a denitrifying soil layer (z_denit, cm, 20). A potential denitrification rate (k_denit, kg N ha⁻¹ d⁻¹, 16) is limited by the nitrate content, soil temperature, and moisture response functions.

$$R_{denit}=\frac{k_{denit}}{z_{denit}}·f_d(T)·{f_d(NO}_3)·f_d(W)$$

(24)

Approaches Based on Explicit Microbial Pools

In CoupModel [68], when denitrifying microbes are explicitly considered, the denitrification rate is a function of their biomass (B_denit, g C m⁻²) and of their activity (M_activity, g C m⁻²). In this approach, NO₃ concentration is obtained by dividing the nitrate amount of the z_th layer for the soil water content of the layer, while NO₂, NO, and N₂O concentrations (N_AnNxOyConc, Appendix A) are estimated by also considering the volumetric anaerobic fraction of the layer (f_Anvol, auxiliary variable). These concentrations and the corresponding amount (N_AnNxOy) in the considered soil layers are employed to define the total denitrification rate (R_denit, g N m⁻² d⁻¹, Equation (25)), as the sum of the nitrogen fluxes (N_AnNO2→AnNO, N_AnNO→AnN2O and N_AnN2O→AnN2, i.e., out fluxes from anaerobic N pools due to microbial growth and respiration, that consumes all N from all the nitrogen anaerobic pools except for N₂) of the denitrification processes steps. The nitrogen content in the anaerobic NO₃ pool, i.e., soil nitrate (AnNO₃, g N m⁻²), is employed. The equation structure describing the flux between N_NO3 and AnNO₂ is also used for estimating the fluxes between AnNO₂ and AnNO and between AnNO and AnN₂O. The equation for growth respiration (N_rg) and maintenance respiration (N_rm) are reported in Appendix A (Appendix A.2).

$$\begin{array}{l}{R}_{denit}=N_{AnNO2\to AnNO}+N_{AnNO\to AnN2O}+N_{AnN2O\to AnN2}\\ N_{{NO}_3\to AnNO2} =min\left[An{NO}_3, (N_{rgNO3}+N_{rmNO3})·M_{activity}·B_{denit}\right]\\ N_{{AnNO}_2\to AnNO}=min\left[An{NO}_2, (N_{rgNO2}+N_{rmNO2})·M_{activity}·B_{denit}\right]\\ N_{AnNO\to AN2O} =min\left[AnNO, (N_{rgNO}+N_{rmNO})·M_{activity}·B_{denit}\right]\\ N_{{AnN}_{2}O\to An{N}_2}=min\left[An{N}_{2}O, (N_{rgN2O}+N_{rmN2O})·{f_d(NO}_3) ·M_{activity}·B_{denit}\right]\end{array}$$

(25)

In DNDC model version 9.5 [79], the consumption rate of N_xO_y through denitrification (R_c,NxOy, kg N ha⁻¹ d⁻¹, Equation (26)) depends on the growth rate of each denitrifier group (u_NxOy), the denitrifiers maximum growth yield on the corresponding substrate (Y_NxOy, kg C kg N⁻¹), the maintenance coefficient on the corresponding substrate (M_NxOy, kg N kg⁻¹ h⁻¹), the denitrifier biomass (B_denit, kg N ha⁻¹), the total N oxides amount (sum of NO₃⁻, NO₂⁻, NO, and N₂O; ∑N_xO_y, kg N ha⁻¹). Furthermore, in the DNDC model, the soil aeration status intended as a redox potential (oxygen or other oxidants content in the soil profile) is simulated. Then, the soil in each layer is divided into aerobic and anaerobic parts where nitrification and denitrification occur, respectively. When the anaerobic parts increase, more substrates (DOC, ammonium, and N oxides) are allocated to the anaerobic microsites to intensify denitrification. When the anaerobic parts decrease, nitrification will be increased due to the reallocation of the substrates into the aerobic microsites.

$$R_{c,NxOy}=\left(\frac{u_{NxOy}}{Y_{NxOy}}+\frac{M_{NxOy}·{N_{x}O}_y}{\sum {N_{x}O}_y}\right)·B_{denit}·f_{d,NxOy}\left(pH\right)·f_d(T)$$

(26)

In the explicit microbial biomass approach of the SPACSYS model [71], the consumption rate (R_c,NxOy, kg N m⁻³ d⁻¹, Equation (26)) of each N oxide (NO₃⁻, NO₂⁻, NO, N₂O) depends on two parameters: the maintenance coefficient on each N oxides (M_NxOy; g C g⁻¹ N d⁻¹, Table A8), and the maximum growth yield on each N oxides (Y_NxOy, g C g⁻¹ N, Table A8). The concentration of each N oxides ([N_xO_y], kg N m⁻³) and of all N oxides (∑[N_xO_y], kg N m⁻³), together with the growth rate of the N_xO_y denitrifiers (R_g,NxOy, kg C m⁻³ d⁻¹) and their total biomass (B_denit, g C m⁻²) are used. The difference from the DNDC model consists in the use of the same soil temperature response function structures for both nitrification and denitrification.

3.1.3. Emissions

In APSIM [67], ARMOSA [56], DAYCENT [11] version 4.7, DNDC version 9.5 [79], and DSSAT model [70] V4.8.2.0 [77], the N₂O emissions rate during nitrification (N₂O_nit, kg N ha⁻¹ d⁻¹, Equation (27)) is estimated as a fraction (r_N2O/nit, unitless, Table A6) of the nitrified N (R_nit, kg N ha⁻¹ d⁻¹).

$${N_{2}O}_{nit}=r_{N2O/nit}·R_{nit}$$

(27)

In the APSIM model, N₂O emissions during denitrification (N₂O_denit, kg N ha⁻¹ d⁻¹, Equation (28)) are obtained using the N₂/N₂O ratio reported by [81], the heterotrophic CO₂ respiration rate (CO_2,resp, µg C g soil⁻¹ d⁻¹), the WFPS and a parameter related to gas diffusivity in the soil at field capacity (g_diff, unitless, 25.1). The soil nitrate concentration considered is the one on a dry weight basis ([NO₃], µg N g⁻¹). In the ARMOSA model, N₂O emissions due to denitrification (N₂O_denit, kg N ha⁻¹ d⁻¹) are also simulated with a modified APSIM approach by applying the N₂/N₂O ratio to the denitrification rate. In Equation (28), the ratio between soil water content (SWC, m³ m⁻³) and saturation soil water content (SWC_sat, m³ m⁻³) substitutes the WFPS.

$$\frac{N_2}{{N_{2}O}_{denit}}=max\left[0.16·g_{diff}, { k}_1·e^{\left(\frac{-0.8·{[NO}_3]}{{CO}_{2,resp}}\right)}\right]·max\left[0.1, \left(\left(1.5·WFPS\right)-0.32\right)\right]$$

(28)

In CERES-EGC [76], N₂O emissions (kg N ha⁻¹ d⁻¹, Equation (29)) from both nitrification and denitrification are simulated by employing site-specific parameters representing the fraction of denitrified N (r_N2O/denit, unitless) and of nitrified N (r_N2O/nit, unitless) emitted as nitrous dioxide.

$$N_{2}O=r_{N2O/nit}·R_{nit}+r_{N2O/denit}·R_{denit}$$

(29)

In CoupModel [68], N₂O and NO emissions (N₂O_nit and NO_nit, Equation (30)) from nitrification can be simulated using the simplified approach or the microbial biomass explicit one for nitrification rate simulation, while the emissions deriving from denitrification require the explicit simulation of the denitrifiers microbial biomass. NO and N₂O emissions from denitrification depend on the nitrification rate (R_nit), the maximum NO (r_NO/nit, unitless, 0.004) or N₂O (r_N2O/nit, unitless, 0.0006) fraction parameters, and on the value of the response function for soil moisture, temperature, and acidity (Equations (45), (74), and (77)). The gaseous N forms can be emitted directly into the atmosphere from the layer in which they were formed, or the transportation of the gases through the soil profile can be simulated explicitly. Emissions from denitrification, when transportation of the gases through the soil profile is not considered, correspond to the nitrogen fluxes (N_NO2→AnNO, N_AnNO→AnN2O, N_AnN2O→AnN2, Equation (25)) estimated for each pool.

$$\begin{array}{l}{N_{2}O}_{nit}=r_{N2O/nit}·f_e\left(W\right)·f_e\left(T\right)·R_{nit}\\ {NO}_{nit} =r_{NO/nit}·f_e\left(W\right)·f_e\left(T\right)·f_e\left(pH\right)·R_{nit}\end{array}$$

(30)

In the CROPSYST model [59,69,73], N₂O emissions (µg N kg⁻¹ d⁻¹) deriving from nitrification are modeled as a fraction of the nitrification rate (µg N kg⁻¹ d⁻¹), obtained through a function of soil moisture and temperature [15].

N₂O emissions from denitrification (N₂O_denit, µg N kg⁻¹ d⁻¹, Equation (31)) are modeled based on concepts and data from [81] through the application of a N₂/N₂O ratio (R_N2/N2O, unitless, Equation (31)), which is dependent on soil nitrate (f_e(NO₃), unitless, Equation (99)), heterotrophic respiration (f_e(CO₂), unitless, Equation (100)), and water content (f_e(W), unitless, Equation (72)) response functions, derived from [80].

N₂ emissions from denitrification are obtained by dividing the denitrification rate by the inverse of the N₂/N₂O ratio plus one.

$$\begin{array}{c}{N_{2}O}_{denit}=\frac{R_{denit}}{\left(1+R_{N2/N2O}\right)}\\ R_{N2/N2O}=min\left[f_e\left({NO}_3\right),f_e\left({CO}_2\right) \right]·f_e\left(W\right)\end{array}$$

(31)

In DAYCENT model [11] version 4.7, N₂O emissions from denitrification are simulated with the approach of [81]. In Equation (32), f_e(NO₃/CO₂) is a unitless function, constrained between 0 and 1, of soil gas diffusivity at field capacity (g_diff, unitless), and f_e(W) is a disturbance-specific multiplier (unitless, not limited to 1, Equation (73)) that considers the effect of soil moisture (WFPS, unitless) on N₂/N₂O ratio (the ratio is obtained by multiplying the two functions).

$${N_{2}O}_{denit}=\frac{R_{denit}}{\left\{1+\left[f_e\left(\frac{{NO}_3}{{CO}_2}\right)·f_e\left(W\right)\right]\right\}}$$

(32)

The NO_x,nit+denit (g N ha⁻¹ d⁻¹, Equation (33)) emissions from soils are estimated on the base of the simulated N₂O emission flux (N₂O_denit and N₂O_nit) by means of a NO_x/N₂O ratio (R_NOx/N2O, unitless, Equation (33)) and of a pulse multiplier (P, unitless) that is employed to take into account pulses in NO_x emissions due to precipitation events.

$$\begin{array}{l}{{{NO}_{x, nit+denit}=R_{NOx/N2O}· N}_{2}O}_{denit}+R_{NOx/N2O}·{N_{2}O}_{nit}·P\\ R_{NOx/N2O}=15.2+\frac{\left\{35.5·atan\left[0.68·\pi ·\left(10·g_{diff}-1.86\right)\right]\right\}}{\pi }\end{array}$$

(33)

In DNDC model version 9.5 [79], NO and N₂O produced in either nitrification or denitrification are subject to further transformation during their diffusion through the soil matrix. The emitted fractions of the total N₂O and of the total N₂ evolved in a day from denitrification (P(N₂O) and P(N₂), unitless, Equation (34)), depending on the air-filled fraction of the total porosity (1-WFPS, unitless) and on an adsorption factor depending on clay content in the soil (f_e(AD), unitless, [0–2]). In the SPACSYS model [71], the emissions rates are derived from the DNDC approach [63].

$$\begin{array}{l}P\left(N_{2}O\right)=\left[0.0006+0.0013·f_e\left(AD\right)\right]+\left[0.013-0.005·f_e\left(AD\right)\right]·\left(1-WFPS\right)\\ P\left(N_2\right)=0.017+\left[0.025-0.0013·f_e\left(AD\right)\right]·\left(1-WFPS\right)\end{array}$$

(34)

In the GHG module of DSSAT [70] V4.8.2.0 [77], the N₂O amount produced in any layer and diffused upward is directly proportional to (1 − WFPS), while the N₂O not diffused from the layer (WFPS) is added to the next day’s total N₂O. NO emissions are estimated through a NO_x/N₂O ratio (R_NOx/N2O, unitless, Equation (35)) and a NO_x pulse multiplier derived from DAYCENT (P, unitless, calculated on the base of rain and snow). The NO_x/N₂O ratio employs the soil gas diffusivity at field capacity (g_diff, unitless, from [81]).

$${NO}_{nit}=\left\{8+\left[\frac{18·\mathit{atan}\left(0.75·\pi ·\left(10·g_{diff}-1.86\right)\right)}{\pi }\right]\right\}·0.5·P·{N_{2}O}_{nit}$$

(35)

N₂O fluxes (N₂O_denit, kg N ha⁻¹ d⁻¹, Equation (36)) from denitrification are calculated using the same approach [81] both in the DAYCENT denitrification subroutine and in the CERES-EGC denitrification subroutine; the only difference is the equation of an auxiliary variable (ratio₁, unitless, Appendix A.2, Appendix A) employed in the estimate of the N₂/N₂O ratio (R_N2/N2O, unitless). The ratio is modified by considering the number of consecutive days (n_day, its maximum used value is 7) during which WFPS > 0.8 using an additional auxiliary variable (ratio₂, unitless, Appendix A.2, Appendix A). N₂ fluxes (N_2,denit, kg N ha⁻¹ d⁻¹) are obtained by removing N₂O emission from the denitrification rate.

$$\begin{array}{c}{N_{2}O}_{denit}=\frac{R_{denit}}{R_{N2/N2O}}\\ R_{N2/N2O}=max\left({ratio}_1, {ratio}_2\right)\end{array}$$

(36)

In EPIC model [62] v. 1102 [78], the Armen Kemanian denitrification method simulates N₂O emissions due to denitrification (N₂O_denit, kg N ha⁻¹ d⁻¹, Equation (37)) as depending on the estimated denitrification rate, the nitrate factor, the water factor, and the respiration factor.

$${N_{2}O}_{denit}=R_{denit}· f_d\left({NO}_3\right)·\left[1-\sqrt{f_d\left(W\right)}\right]·\left[1-{f_d\left({CO}_2\right)}^{0.25}\right]$$

(37)

In the original EPIC denitrification method, N₂ emission due to denitrification (kg N ha⁻¹ d⁻¹, Equation (38)) is estimated as a fraction of denitrification using a parameter describing the N₂ fraction partitioning (r_N2/denit, unitless, between 0.1 and 0.9) while N₂O emissions are complimentary estimated (N₂O,_denit, kg N ha⁻¹ d⁻¹, Equation (38)).

$${N_{2}O}_{denit}=R_{denit}-\left(r_{N2/denit}·R_{denit}\right)$$

(38)

In the STICS model [60], N₂O emissions during nitrification (N₂O_nit, kg N ha⁻¹ d⁻¹, Equation (39)) are obtained through the ratio between N₂O and the total nitrification (r_N2O/nit, unitless). N₂O emissions during denitrification (N₂O_denit, kg N ha⁻¹ d⁻¹, Equation (39)) are obtained by assuming a constant ratio (r_N2O/denit, unitless) between N₂O emissions and total denitrification.

$$\begin{array}{c}{N_{2}O}_{nit}=r_{N2O/nit}·R_{nit}·{NH}_4\\ {N_{2}O}_{denit}={r_{N2O/denit}·R}_{denit}\end{array}$$

(39)

3.1.4. Environmental Factors

Soil Temperature Factor

In the APSIM model [67], the temperature factor limiting nitrification is the same as that used for the mineralization estimate [72]. It consists of an exponential function, whose minimum value (0) is obtained for a 0 °C soil temperature and whose maximum value (1) is obtained for a 30 °C soil temperature [84]. The temperature factor (Figure 1, Equation (40)) limiting denitrification is an exponential function of the soil temperature (T, °C) [67].

$$f_d\left(T\right)=0.1 · e^{(0.46 ·T) }$$

(40)

In the ARMOSA model, the same soil temperature factor (f(T), unitless, Equation (41)) is employed both for nitrification and denitrification, and it is derived from the SOILN approach [75]. It consists of an exponential function, constrained between 0 and 1, having a Q₁₀-value as a base (t_Q10, unitless, between 1.5 and 4) that describes the response to a 10 °C soil temperature change. A base temperature (T_opt, °C, 20) at which the temperature effect is equal to 1 is also employed. CROPSYST model [59,69,73] employs the same response function (Equation (41)) to limit only the nitrification rate.

$$f(T)={t_{Q10}}^{\left(\frac{T-T_{opt}}{10}\right)}$$

(41)

In the SPACSYS model [71], a Q₁₀ equation having different Q₁₀ for the various processes is employed, while in DAYCENT model 4.7 [11], the response function of nitrification to soil temperature, f_n(T), is represented by a generalized Poisson density function.

In CERES-EGC [76], the response function of nitrification to soil temperature (T, °C) is an exponential function (Equation (42)) that is not limited to 1 and employs a Q₁₀ factor parameter (t_Q10, unitless, 2.1) describing the relative increase in the process activity for a 10 °C increase in soil temperature.

$$f_n\left(T\right)=e^{\left[\frac{\left(T-20\right)·ln\left(t_{Q10}\right)}{10}\right]}$$

(42)

The exponential response function of denitrification to soil temperature (Equation (43)) is not limited to 1 and employs a threshold temperature parameter (T_denit, °C, 11) and two Q₁₀ factors: one for low temperature (t_Q10,1, unitless, 89.0) and one for high temperature (t_Q10,2, unitless, 2.1).

$$f_d\left(T\right)=\left\{\begin{array}{cc}{e}^{\left[\frac{\left(T-T_{denit}\right)·ln\left(t_{Q10,1}\right)-9ln\left(t_{Q10,2}\right)}{10}\right]}\hfill & {if T<T}_{denit}\hfill \\ e^{\left[\frac{\left(T-20\right)·ln\left(t_{Q10,2}\right)}{10}\right]}\hfill & if T\ge T_{denit}\hfill \end{array}\right.$$

(43)

In CoupModel [68], the response function of denitrification and of nitrification to soil temperature (T, °C, for the topsoil layer, it is equal to the air temperature) in a considered layer can be selected among three different options (Figure 1, Equation (44)). A function that becomes a Q₁₀-type function above a certain temperature threshold (f(T)₁), a Q₁₀-type function for the whole range of temperatures (f(T)₂), and a Ratkowsky function consisting in a quadratic function (f(T)₃). The employed parameters are the following: response to a 10 °C soil temperature change on the microbial activity, nitrification and denitrification (t_Q10, unitless, 2), base temperature for the microbial activity, nitrification and denitrification at which the response is 1 (T_opt, °C, 20), threshold temperature for the microbial activity, nitrification and denitrification below which the response is stronger than above and ceases at 0 °C (T_Q10thres, °C, 5), minimum temperature for nitrification and denitrification (T_min, °C, −8), and temperature at which the response of nitrification and denitrification is equal to 1 (T_max, °C, 20).

$$\begin{array}{l}{f\left(T\right)}_1={t_{Q10}}^{\left(\frac{T-T_{opt}}{10}\right)}\\ {f\left(T\right)}_2=\frac{T}{T_{Q10thres}}·{f_d\left(T\right)}_1\\ f{\left(T\right)}_3=\left\{\begin{array}{cc}1\hfill & \hfill if T>T_{max}\\ {\left(\frac{T-T_{min}}{T_{max}-T_{min}}\right)}^2& \hfill if T_{min}<T<T_{max} \\ 0\hfill & \hfill if T<T_{min}\end{array}\right.\end{array}$$

(44)

The response function (f_e(T), unitless, Equation (45)) to soil temperature for N₂O and NO emissions during nitrification employs three parameters: the maximum (g_TmaxNxO, °C, 33.5) and optimum (g_ToptNxO, °C, 23.5) soil temperature for the formation of nitrous trace gases during nitrification, and the parameter determining the response function shape (g_TshapeNxO, unitless, 1.5).

$$\begin{array}{c}{f}_e(T)={\left(\frac{g_{TmaxNxO}-T}{g_{TmaxNxO}-g_{ToptNxO}}\right)}^{f(T_{exp})}\\ f\left(T_{exp}\right)=g_{TshapeNxO}·\frac{T-g_{ToptNxO}}{g_{TmaxNxO}-g_{ToptNxO}}\end{array}$$

(45)

In DNDC model version 9.5 [79], the soil temperature (T, °C) factor employed in the nitrification is an exponential function of soil temperature (Figure 1, Equation (46)).

$$f_n\left(T\right)={3.503}^{\left[\frac{(60-T)}{25.78}\right]}·e^{\left[\frac{3.503·(T-34.22)}{25.78}\right]}$$

(46)

The soil temperature factor employed in the denitrification estimate (Figure 1, Equation (47)) is a Q₁₀-type function with a base equal to 2 and an optimum temperature of 22.5 °C, with a soil temperature threshold parameter (T_max,denit, °C, 60). The function is equal to zero when the soil temperature is higher than the threshold value.

$$f_d\left(T\right)=2^{\frac{T-22.5}{10}} if T\le T_{max,denit}$$

(47)

In DSSAT model [70] V4.8.2.0 [77], two functions are used for the response of nitrification to soil temperature: the first one is constrained between 0 and 1 and describes soil temperature (T, K) effect on nitrification (f_n1(T), unitless, Figure 1, Equation (48)), while the second one is a function (f_n2(T), unitless, Figure 1, Equation (48)) of the temperature response function of the previous time step (f_n1(T)_t−1, unitless).

$$\begin{array}{c}{f}_{n1}\left(T\right)=e^{\left(\frac{-6572}{T}+21.4\right)}\\ f_{n2}\left(T\right)=min\left[0.075·{f_{n1}{\left(T\right)}_{t-1}}^2,1\right]\end{array}$$

(48)

The response function of denitrification to soil temperature (T, K) is only present in the CERES denitrification subroutine, and it is limited between 0 and 1 (f_d(T), unitless, Figure 1, Equation (49)).

$$f_d\left(T\right)=0.1·e^{0.046·T}$$

(49)

In EPIC model [62] v. 1102 [78], the response function of nitrification to soil temperature (T, °C) is a linear function (Equation (50)).

$$f_n\left(T\right)=0.41·(T-5)$$

(50)

In the STICS model [60], the response function of nitrification to soil temperature (T, °C) is limited between 0 and 1 (Figure 1, Equation (51)), and it is defined by the following parameters: minimum cardinal temperature for nitrification (T_min,nit, °C), optimum cardinal temperature for nitrification (T_opt,nit, °C), and maximum cardinal temperature for nitrification (T_max,nit, °C).

$$f_n\left(T\right)=\left\{\begin{array}{c}\frac{T-T_{min,nit}}{T_{opt,nit}-T_{min,nit}} if T\le T_{opt,nit}\\ \frac{T-T_{max,nit}}{T_{opt,nit}-T_{max,nit}} if T\ge T_{opt,nit}\end{array}\right.$$

(51)

The response function of denitrification to soil temperature (T, °C) is limited between 0 and 1 (Figure 1, Equation (52)), and it is defined by two cardinal temperatures for denitrification (T_1,denit, °C, 11; T_2,denit, °C, 20).

$$f_d\left(T\right)=\left\{\begin{array}{ll}{e}^{\left[\left(T-T_{1,denit}\right)·0.449-0.668\right]}& if T\le T_{1,denit} \\ e^{\left[\left(T-T_{2,denit}\right)·0.0742\right]}& if T>T_{1,denit}\end{array}\right.$$

(52)

Soil Moisture Factor

In the APSIM model [67], the soil moisture factor limiting nitrification is a trapezoidal function whose value is 0 at the lower limit soil water content and at the saturation soil water content (SWC_sat), and it is equal to 1 at the drained upper limit. All the considered soil water contents are volumetric ones [84]. The soil moisture factor limiting denitrification (Figure 2, Equation (53)) is defined by the following parameters: water content at which denitrification ceases (SWC_lim, in the default configuration, is equal to the value of WFPS at DUL) and empirical coefficient (x, in the default configuration equal to 1) [67].

$$f_d\left(W\right)={\left(\frac{SWC-{SWC}_{lim}}{{SWC}_{sat}-{SWC}_{lim}}\right)}^x$$

(53)

In ARMOSA, the soil moisture effect on nitrification is described through a response function (f_n(W), unitless, Figure 2, Equation (54)) limited between 0 and 1, which employs four soil water content thresholds (SWC_min, SWC_optmin, SWC_optmax, and SWC_max, m³ m⁻³, Appendix A.2, Appendix A) that are estimated as fractions of the saturation water content (SWC_sat, m³ m⁻³). The function is defined by the following parameters: microbial activity below SWC_min (f_min, unitless, 0), microbial activity above SWC_max (f_max, unitless, 0.5), microbial activity curvature coefficients (a and b, unitless, 1). When SWC ≤ SWC_min, the response function is equal to f_min; when SWC > SWC_max, the response function is equal to f_max, while the function is equal to 1 when SWC is comprised between SWC_optmin and SWC_optmax.

$$\begin{array}{l}{f}_n(W)=\left\{\begin{array}{cc}{f}_{min}+\left(1-f_{min}\right)·{\left(\frac{SWC-{SWC}_{min}}{{SWC}_{optmin}-{SWC}_{min}}\right)}^a& 〈1〉\\ f_{max}+\left(1-f_{max}\right)·{\left(\frac{{SWC}_{max}-SWC}{{SWC}_{max}-{SWC}_{optmax}}\right)}^b& 〈2〉\end{array}\right.\\ {〈1〉 SWC}_{min}<SWC\le {SWC}_{optmin}\\ 〈2〉 {SWC}_{optmax}<SWC\le {SWC}_{max}\end{array}$$

(54)

The soil moisture effect on denitrification is described through a response function, constrained between 0 and 1 (f_d(W), unitless, Figure 2, Equation (55)), that is derived from the APSIM approach (Equation (53)). This response function uses three parameters: the saturation threshold (thr_sat, unitless, 0.6), an empirical coefficient (x, unitless, 1, between 0.9 and 5), and a lower threshold for soil water content (thr_denit, unitless, 0.05) under which no denitrification occurs (response function equal to 0).

$$f_d(W)={\left(\frac{SWC-{thr}_{sat}·{SWC}_{sat}}{{SWC}_{sat}-{thr}_{sat}·{SWC}_{sat}}\right)}^x$$

(55)

In CERES-EGC [76], the nitrification response function to soil water content (Equation (56)) increases linearly from a minimum WFPS value (WFPS_min,nit, %, 0.1) to an optimum value (WFPS_opt,nit, %, 0.6). The function then decreases linearly to a maximum value (WFPS_max,nit, %, 0.8). It is equal to zero otherwise.

$$f_n\left(W\right)=\left\{\begin{array}{c}\frac{WFPS-{WFPS}_{min,nit}}{{WFPS}_{opt,nit}-{WFPS}_{min,nit}} if {WFPS}_{min,nit}<WFPS\le {WFPS}_{opt,nit} \\ \frac{{WFPS}_{max,nit}-WFPS}{{WFPS}_{max,nit}{-WFPS}_{opt,nit}}if {WFPS}_{opt,nit}\le WFPS{<WFPS}_{max,nit}\end{array}\right.$$

(56)

The denitrification response function to soil water content (Equation (57)) is equal to zero when the soil WFPS is lower than a threshold value (WFPS_denit, %, 0.62); otherwise, it consists of a function having a parameter as exponent (x, unitless, 1.74).

$$f_d\left(W\right)={\left(\frac{WFPS-{WFPS}_{denit}}{1-{WFPS}_{denit}}\right)}^{x}if WFPS\ge {WFPS}_{denit}$$

(57)

In CoupModel [68], the soil moisture response function for denitrification (Figure 2, Equation (58)) is estimated differently on the base of the simulated soil water content (SWC, m³ m⁻³) and of the soil water content at saturation (SWC_sat, m³ m⁻³). The response function is defined by the following parameters: a coefficient in the function for soil moisture effect on denitrification (p_θDp, unitless, 10) and a water content range from saturation in the function for soil moisture on denitrification (p_θDRange, %, 10). The function is equal to 1 when SWC is equal to SWC_sat, while it is equal to zero when SWC − SWC_sat > p_θDp.

$$f_d\left(W\right)={\left(\frac{SWC-{SWC}_{sat}-p_{\theta DRange}}{p_{\theta DRange}}\right)}^{p_{\theta Dp}} if SWC-{SWC}_{sat}<p_{\theta Dp}$$

(58)

The soil moisture response function for nitrification (Figure 2, Equation (59)) is estimated differently on the base of the simulated soil water content at saturation and at wilting point (SWC_wilt, m³ m⁻³) and is defined by the following parameters: saturation activity in soil moisture response function (p_θsatact, unitless, 0.6, 0 is equal to no activity, 1 is equal to optimum activity at saturation), water content interval lower limit in the soil moisture response for nitrification and denitrification (p_θLow, %, 13, range 8–15), the coefficient for the soil moisture function (p_θp, unitless, 1 corresponds to a linear response, 0–1 corresponds to a convex response, >1 corresponds to a concave response), water content interval upper limit in the soil moisture response function for nitrification and denitrification (p_θUpp, %, 8, range 1–10). The function is equal to p_θsatact when SWC is equal to SWC_sat, while it is equal to zero when SWC < SWC_wilt.

$$f_n\left(W\right)=min\left[{\left(\frac{{SWC}_{sat}-SWC}{p_{\theta Upp}}\right)}^{p_{\theta p}}·\left(1-p_{\theta satact}\right)+p_{\theta {satact}^{\prime }}{\left(\frac{SWC-{SWC}_{wilt}}{p_{\theta Low}}\right)}^{p_{\theta p}} \right]$$

(59)

In the CROPSYST model [59,69,73], the response function of nitrification (Figure 2, Equation (60)) to the volumetric soil water content (SWC, m³ m⁻³) is modeled with the SOILN approach [74,75]. The response function is equal to zero below the wilting point (SWC_wilt, %); it increases to one in the interval delimited by a parameter (p_θLow, %, 13), and near the saturation water content (SWC_sat, %), it decreases to a saturation activity (p_θsatact, unitless, 0.6, range 0–1) in an interval confined by a parameter (p_θUpp, %, 8). The shape of the response curve between p_θLow and p_θUpp is given by a parameter (p_θp, unitless), the linear response is obtained with a value of 1; between 0 and 1, the response function is convex, and for values higher than 1, the response is concave. p_θLow is the water content interval defining increasing activity from 0 (no activity) at SWC_wilt to 1 (optimum activity) at p_θLow + SWC_wilt; its normal range is 8–15, depending on soil type. p_θUpp is the water content interval defining decreasing activity from 1 (optimum activity) at SWC_sat − p_θUpp to the activity given by parameter p_θsatact at SWC_sat; its normal range is 1–10, depending on soil type.

$$\begin{array}{l}{f}_n\left(W\right)=\left\{\begin{array}{c}{p}_{\theta satact}+\left(1-p_{\theta satact}\right)·{\left(\frac{{SWC}_{sat}-SWC}{p_{\theta Upp}}\right)}^{p_{\theta p}} 〈1〉\hfill \\ {\left(\frac{SWC-{SWC}_{wilt}}{p_{\theta Low}}\right)}^{p_{\theta p}} 〈2〉\hfill \end{array}\right.\\ 〈1〉 if{SWC}_{sat}-p_{\theta Upp}<SWC<{SWC}_{sat}\\ 〈2〉 if {SWC}_{wilt}<SWC<{SWC}_{wilt}+p_{\theta Upp}\end{array}$$

(60)

The response function (f_d(W), unitless, Equation (61)) describing WFPS (unitless) effect on denitrification is limited, between 0 and 1 [80], its parameters values vary with soil texture (sandy, medium and fine): a (1.56, 4.82, and 60.0), b (12.0, 14.0, and 18.0), c (16.0, 16.0, and 22.0), and d (2.01, 1.39, and 1.06).

$$f_d\left(W\right)=\frac{a}{b^{\left[\frac{c}{b^{(d·WFPS)}}\right]}}$$

(61)

In DAYCENT model 4.7 [11], the response function of nitrification and denitrification, f_n(W) and f_d(W), consider the second and the third soil layer moisture status only (Figure 2). The response function for nitrification (Equation (62)) employs available soil water content (SWC_avail, m³ m⁻³) and the weighted average of the WFPS of the considered layers, respectively, for soils drier or wetter than field capacity (SWC_fc, m³ m⁻³).

$$f_n\left(W\right)=\left\{\begin{array}{cc}\frac{1}{1+30·e^{-9·{SWC}_{avail}}}\hfill & \hfill if SWC\le {SWC}_{fc}\\ \frac{-1}{1-{SWC}_{fc}}·\left({WFPS}_{avg}-1\right)\hfill & \hfill else\end{array}\right.$$

(62)

The WFPS curve (Equation (63)) of the denitrification submodel [81] was modified [11] to stop the denitrification process for WFPS < 55%, and it is defined by a parameter corresponding to the WFPS level at which the denitrification reaches half of its maximum velocity (a, unitless). The WFPS [11,85] for the two response functions is calculated as a function of gravimetric soil water content (θ_g, g water g soil⁻¹) and bulk density (BD, g cm⁻³).

$$\begin{array}{l}{f}_d\left(W\right)=0.45+\frac{atan\left[0.6·\pi ·\left(0.1·WFPS-a\right)\right]}{\pi }\\ WFPS={\theta }_g·\frac{BD}{\left(1-\frac{BD}{2.65}\right)}\end{array}$$

(63)

In DNDC model version 9.5 [79], a soil moisture factor (Figure 2, Equation (64)) is employed in the nitrification estimate, for which the soil water content is expressed as water-filled porosity (WFPS).

$$f_n\left(W\right)=\left\{\begin{array}{cc}0.8+0.21·\left(1-WFPS\right)\hfill & \hfill if WFPS>0.05 \\ 0\hfill & \hfill if WFPS\le 0.05\end{array}\right.$$

(64)

In DSSAT model [70] V4.8.2.0 [77], the response function (f_n(W), unitless, Figure 2, Equation (65)) of nitrification to soil water content (SWC, m³ m⁻³) is based on water-filled porosity (WFPS, unitless), and it is limited between 0 and 1. The function uses as soil water content thresholds the drained upper limit (DUL, m³ m⁻³) and the saturation water content (SWC_sat, m³ m⁻³). The WFPS is obtained as the ratio between SWC and SWC_sat.

$$f_n\left(W\right)=\left\{\begin{array}{cc}-2.5·WFPS+2.55\hfill & \hfill if SWC>DUL\\ 1\hfill & \hfill if SWC<DUL and WFPS>0.4\\ 3.15·WFPS-0.1\hfill & \hfill else\end{array}\right.$$

(65)

In the DAYCENT denitrification subroutine, the response function of denitrification (f_d(W), unitless, Equation (66)) to soil moisture is constrained between 0 and 1 and considers the soil gas diffusivity at field capacity (g_diff, unitless), the WFPS and an auxiliary variable (CO_2correct, Equation (91)).

$$\begin{array}{l}{f}_d\left(W\right)=0.45+\frac{atan\left\{0.6·\pi ·\left[10·WFPS-\left(9.0-M·{CO}_{2correct}\right)\right]\right\}}{\pi }\\ M=\left\{min\left[0.113, g_{diff}·(-1.25)\right]\right\}+0.145 \end{array}$$

(66)

In the CERES denitrification subroutine, the response function of denitrification (f_d(W), unitless, Equation (67)) to soil moisture is constrained between 0 and 1 and is calculated when soil moisture (SWC, m³ m⁻³) is higher than the drained upper limit (DUL, m³ m⁻³).

$$f_d\left(W\right)=1-\left(\frac{{SWC}_{sat}-SWC}{{SWC}_{sat}-DUL}\right)$$

(67)

In EPIC model [62] v. 1102 [78], the Armen Kemanian denitrification method employs a water factor (f_d(W), Equation (68)) that considers the soil layer porosity (PO, m³ m⁻³), its soil water storage (SWT, m³ m⁻³, fraction of field capacity), its thickness (z_layer, m), and its clay amount (CLAY, %).

$$\begin{array}{c}{f}_d\left(W\right)=\left\{\begin{array}{cc}\frac{1}{1+{\left(\frac{1-AIRV}{0.9+0.01·CLAY}\right)}^{-60}}\hfill & \hfill if \left(\frac{1-AIRV}{0.9+0.01·CLAY}\right)>0.8\\ 0\hfill & \hfill else \end{array}\right. \hfill \\ AIRV=\frac{PO-SWT}{z_{layer}}\hfill \end{array}$$

(68)

In the SPACSYS model [71], the water-filled pore space (WFPS) response function is applied only to nitrification (Figure 2, Equation (69)), and it is expressed with a quadratic function, with the WFPS estimate approach derived from [86,87]. Its value depends on volumetric soil water content (SWC, m³ m⁻³), soil bulk density (BD, g cm⁻³), and soil particle density (PD, g cm⁻³) parameters.

$$\begin{array}{l}{f}_n\left(W\right)=\left\{\begin{array}{c}min\left[1;\left(-11.25·{WFPS}^2+11.75·WFPS-1.9\right)\right] if 0.3\le WFPS\le 0.75\\ 0.6 if 0.3<WFPS or WFPS>0.75\end{array}\right.\\ WFPS=\frac{SWC}{1-\frac{BD}{PD}}\end{array}$$

(69)

In the STICS model [60], the response function (Equation (70)) of nitrification to soil water content (SWC, mm water cm⁻¹ soil) is limited between 1 and 0, and it employs an optimal water content parameters (SWC_opt,nit, unitless, 1) that is different from the one used for mineralization, and a minimal soil water content for nitrification process (SWC_min,nit, unitless, 0.67). All the soil water content parameters are expressed as a proportion of field capacity water content (SWC_fc, mm water cm⁻¹ soil).

$$f_n\left(W\right)=\frac{SWC-{SWC}_{min,nit}·{SWC}_{fc}}{\left({SWC}_{opt,nit}-{SWC}_{min,nit}\right)·{SWC}_{fc}}$$

(70)

The response function of denitrification to soil moisture is defined using the auxiliary variable saturation soil status (WFPS, unitless), and it is related to the mineralization process through the reference temperature for soil mineralization parameter (T_miner, °C, 15). The function (Figure 2, Equation (71)) is limited between 0 and 1. It considers the amount of water remaining in the soil macroporosity (SWC_sat, mm) and the bulk density (g cm⁻³).

$$\begin{array}{c}{f}_d\left(W\right)={\left[\frac{WFPS-\left(0.62-\frac{T-T_{miner}}{100}\right)}{1-\left(0.62-\frac{T-T_{miner}}{100}\right)}\right]}^{1.74} \\ WFPS=\frac{SWC+{SWC}_{sat}}{10·\left(1-\frac{BD}{2.66}\right)}\end{array}$$

(71)

In the CROPSYST model [59,69,73], the response function (f_e(W), unitless, Equation (72)) describing the WFPS (unitless) effect on N₂/N₂O ratio for denitrification gas fluxes is not constrained between 0 and 1, and it is derived from [80].

$$f_e\left(W\right)=\frac{1.4}{{13}^{\left[\frac{17}{{13}^{\left(2.2·WFPS\right)}}\right]}}$$

(72)

In DAYCENT model 4.7 [11], a WFPS effect on the N₂/N₂O ratio (f_e(W), Equation (73)) is also applied.

$$f_e\left(W\right)=max\left(0.1, 0.015·WFPS·100-0.32\right)$$

(73)

In CoupModel [68], the soil moisture response function limiting the production of NO and N₂O during nitrification (f_e(W), unitless, Equation (74)) is defined by two parameters: the relative saturation level in the response function for soil moisture when NO or N₂O is formed during nitrification (g_θsatcrit, unitless, Table A8, Appendix A.3, Appendix A) and the parameter describing the shape of the moisture response function for NO or N₂O emissions (g_θsatform, unitless, Table A8, Appendix A.3, Appendix A).

$$f_e\left(W\right)=1-\frac{1}{1+e^{\left(\frac{SWC/{SWC}_{sat}-g_{\theta satcrit}}{g_{\theta satform}}\right)}}$$

(74)

Soil Acidity Factor

In the APSIM model [67], the soil acidity factor limiting nitrification is a trapezoidal function [84] whose value is equal to 0 when pH < pH_min (unitless, 4.5) or pH > pH_max (9, unitless) and whose value is equal to 1 for pH_optmin ≤ pH ≤ pH_optmax (unitless, 6 and 8, respectively). The response function of nitrification to soil acidity in ARMOSA, CROPSYST [59,69,73], and STICS [60] models employs the SOILN approach [74,75]: it is a linear function (Figure 3, Equation (75)) defined by two parameters. The function is equal to 0 for pH < pH_min (unitless, 3), while it is equal to 1 for pH > pH_max (unitless, 5.5).

$$f_n\left(pH\right)=\frac{pH-{pH}_{min}}{{pH}_{max}-{pH}_{min}}$$

(75)

In CoupModel [68], the response function of denitrification (Figure 3, Equation (76)) to soil acidity is defined by two parameters: the pH half rate (d_pHrate, unitless, 4.25) and a shape coefficient (d_pHshape, unitless, 0.5).

$$f_d\left(pH\right)=1-\frac{1}{1+e^{\left(\frac{pH-d_{pHrate}}{d_{pHshape}}\right)}}$$

(76)

In CoupModel [68], the response function of NO and N₂O production during nitrification to soil acidity (Equation (77)) employs a parameter (pH_min, unitless, 4.7) describing the pH value below, in which the function is equal to 1.

$$f_e\left(pH\right)={pH}_{min}-pH$$

(77)

In DAYCENT model 4.7 [11,85], the response function of nitrification to soil acidity (Equation (78)) is calculated as an inverse function of the tangent function (atan is a standard C arctangent function from the library math.h).

$$f_n\left(pH\right)=\mathit{atan}(pH, a)$$

(78)

In DNDC model version 9.5 [79], a pH factor for denitrification is employed (f_d(pH)_NxOy, Figure 3, Equation (79)).

$$f_d{\left(pH\right)}_{NxOy}=\left\{\begin{array}{c}1-\frac{1}{e^{(pH-4.25)/0.5}} if {N_{x}O}_y={NO}_3 \\ 1-\frac{1}{e^{\left(pH-5.25\right)/1}} if {N_{x}O}_y={NO}_2 or NO\\ 1-\frac{1}{e^{\left(pH-6.25\right)/1.5}} if {N_{x}O}_y=N_{2}O\end{array}\right.$$

(79)

In DSSAT model [70] V4.8.2.0 [77], the response function of nitrification to soil acidity (f_n(pH), unitless) is limited between 0 and 1. It is equal to 0 and 1 when pH < pH_min and when pH > pH_opt, respectively, and linear in between (Figure 3, Equation (80)).

$$f_n\left(pH\right)=min(1, 0.33·pH-1.36)$$

(80)

In EPIC model [62] v. 1102 [78], a trapezoidal response function (Figure 3, Equation (81)) of nitrification to soil acidity (pH, unitless) is employed: it is constrained between 0 and 1 and defined by two parameters: pH optimum minimum threshold (pH_optmin, unitless, 7) and pH optimum maximum threshold (pH_optmax, unitless, 7.4).

$$f_n\left(pH\right)=\left\{\begin{array}{cc}\left(0.307·pH\right)-1.269\hfill & \hfill if pH<{pH}_{optmin}\\ 1\hfill & \hfill if {pH}_{optmin}\le pH\le {pH}_{optmax}\\ 5.367-0.599·pH\hfill & \hfill if pH>{pH}_{optmax}\end{array}\right.$$

(81)

In the SPACSYS model [71], the response functions of nitrification and denitrification to soil acidity are unitless and limited between 0 and 1 (each step of the denitrification process presents its own function, Figure 3, Equation (82)).

$$\begin{array}{l}{f}_n\left(pH\right)=e^{{-\left(\frac{pH-6.6}{2}\right)}^2}\\ f_{d,{NO}_3}\left(pH\right)=1-\frac{1}{1+e^{\left(\frac{pH-4.25}{0.5}\right)}}\\ f_{d,NO}\left(pH\right)=\frac{1}{1+e^{{\left(\frac{pH-4.5}{2.5}\right)}^{5.5}}}\\ f_{{d,NO}_2}\left(pH\right)=e^{{-\left(\frac{pH-6.2}{2}\right)}^2}\\ f_{{d,N}_{2}O}\left(pH\right)=e^{{-\left(\frac{pH-8.2}{2}\right)}^2}\end{array}$$

(82)

Substrate Concentration Effect

In CERES-EGC [76], the response function of nitrification (Equation (83)) to soil ammonium content (mg N kg soil⁻¹) employs a half-saturation constant parameter (K_m,nit, mg N kg soil⁻¹, 10) that is modified on the base of the soil water content value.

$$f_n\left({NH}_4\right)=\frac{{NH}_4}{K_{m,nit}·SWC+{NH}_4}$$

(83)

In the response function of denitrification (Equation (84)) to soil nitrate content (mg N kg soil⁻¹), using a dedicated half-saturation constant (K_m,denit, mg N kg soil⁻¹, 22), the soil water content is not considered.

$$f_d\left({NO}_3\right)=\frac{{NO}_3}{K_{m,denit}+{NO}_3}$$

(84)

In CoupModel [68], the response function of denitrification (Equation (85)) to nitrate concentration ([NO₃], mg N L⁻¹) employs a parameter describing the half-saturation constant (K_m, mg N L⁻¹, 10, range 5–15), i.e., the nitrate concentration at which the activity is half of the activity at optimum nitrate concentration.

$$f_d\left({NO}_3\right)=\frac{\frac{\left[{NO}_3\right]}{SWC·z_{layer}}}{\left(\frac{\left[{NO}_3\right]}{SWC·z_{layer}}\right)+K_m}$$

(85)

The response function of nitrification rate (Equation (86)) to nitrate and ammonium ([NH₄], mg N L⁻¹) concentrations in the simplified approach, i.e., when microbes are not considered, employs two parameters: the nitrate–ammonium ratio (r_NO3/NH4, unitless, 8, range 1–15) and the specific nitrification rate (k_nit, d⁻¹, 0.2).

$$f_n\left({NH}_4,{NO}_3\right)=max\left(0, \frac{\left[{NH}_4\right]-\left[{NO}_3\right]}{r_{NO3/NH4}}\right)·k_{nit}$$

(86)

The response function of nitrification rate (Equation (87)) to ammonium concentration in the microbial biomass explicit approach employs the nitrification half rate parameters (K_m, mg N L⁻¹, 6.18).

$$f_n\left({NH}_4\right)=\frac{\frac{\left[{NH}_4\right]}{SWC·z_{layer}}}{\frac{\left[{NH}_4\right]}{SWC·z_{layer}}+K_m}$$

(87)

In CROPSYST [59,69,73], the response function (f_d(NO₃), g N ha⁻¹ d⁻¹, Equation (88)) describing the maximum denitrification for a certain NO₃ (µg N g⁻¹) soil level is derived from [80].

$$f_d\left({NO}_3\right)=11.00+\frac{40.00·atan\left[\pi ·0.002·({NO}_3-180)\right]}{\pi }$$

(88)

The response function (f_d(CO₂), g N ha⁻¹ d⁻¹, Equation (89)) describing the maximum denitrification for a certain soil respiration (CO_2,resp, kg C N ha⁻¹ d⁻¹) level is derived from [80].

$$f_d\left({CO}_2\right)=\frac{24}{\left(1+\frac{200}{e^{0.35·{CO}_{2,resp}}}\right)}-100$$

(89)

In DAYCENT model 4.7 [11], the two substrate concentration effect functions (f_d(NO₃), f_d(CO₂), µg N g soil⁻¹ d⁻¹, Equation (90)) are not limited between 0 and 1 (they cannot be negative), but they correspond to the potential total N flux not limited by CO₂ and H₂O for f_d(NO₃) by NO₃ and H₂O for f_d(CO₂) [81].

$$\begin{array}{l}{f}_d\left({NO}_3\right)=atan\left({NO}_3,a\right)\\ f_d\left({CO}_2\right)=0.1·{\left({CO}_2\right)}^{1.3}-0.1\end{array}$$

(90)

In DSSAT model [70] V4.8.2.0 [77], the DAYCENT denitrification subroutine employs a denitrification response function to NO₃⁻ (f_d(NO₃), kg N ha⁻¹ d⁻¹, Equation (91)) that has a lower bound equal to zero.

$$f_d\left({NO}_3\right)=1.556+\left(\frac{76.91}{\pi }\right)·atan\left[\pi ·0.00222·({NO}_3-9.23)\right]$$

(91)

In the DAYCENT denitrification subroutine, the denitrification response function to CO₂ (f_d(CO₂), unitless, Equation (92)) is derived from [81] and has a lower bound equal to zero. It considers a minimum amount of nitrate (NO_3,min, kg N ha⁻¹ d⁻¹, 0.1) and an auxiliary variable (CO_2correct, Equation (91)), derived from the CO₂ produced daily (CO_2,resp) in the first two soil layers (first soil layer, L = 0, and second soil layer, L = 1, the first soil layer also includes the mulch layer).

$$\begin{array}{l}{f}_d\left({CO}_2\right)=\left[0.1·{{ CO}_{2correct}}^{1.3}\right]-{NO}_{3,min}\\ {CO}_{2correct}=\left\{\begin{array}{cc}\left[{CO}_2\right]\hfill & \hfill if WFPS\le {thr}_{WFPS}\\ \left[{CO}_2\right]·\left(1+a·(WFPS-{thr}_{WFPS}\right))& \hfill else\end{array}\right.\\ \left[{CO}_2\right] (L)=\left\{\begin{array}{cc}{CO}_{2, resp}\left(0\right)+{CO}_{2, resp}\left(1\right)\hfill & \hfill if L=1\\ {CO}_{2, resp}\left(L\right)\hfill & \hfill else\end{array}\right.\\ {thr}_{WFPS}=\left\{\begin{array}{c}0.8 if g_{diff}\ge 0.15\\ \frac{g_{diff}·250+43}{100} else\end{array}\right.\\ a=\left\{\begin{array}{cc}0.004\hfill & \hfill if g_{diff}\ge 0.15\\ -0.1·g_{diff}+0.019\hfill & \hfill else\end{array}\right.\end{array}$$

(92)

In the CERES denitrification subroutine, the water-extractable soil carbon amount (C_W, Equation (93)) depends on the availability of C from the humic fraction (C_SSOM) and of the fresh C from the carbohydrate pool (C_LIT).

$$C_W=24.5+0.0031·\left(C_{SSOM}+0.2·C_{LIT}\right)$$

(93)

In EPIC model [62] v. 1102 [78], the Armen Kemanian denitrification method uses a nitrate factor (f_d(NO₃), Equation (94)).

$$f_d\left({NO}_3\right)=\frac{max\left(1e^{-5},\frac{1000·{NO}_3}{WT}\right)}{max\left(1e^{-5},\frac{1000·{NO}_3}{WT}\right)+60}$$

(94)

In the Armen Kemanian denitrification method, the respiration factor (f_d(CO₂), Equation (95)) considers the CO₂ respiration (CO_2,resp, kg C N ha⁻¹ d⁻¹) of the layer and the soil weight (WT).

$$f_d\left({CO}_2\right)=min\left(1, \frac{\frac{1000·{CO}_{2,resp}}{WT}}{50}\right)$$

(95)

In the SPACSYS model [71], the substrate concentration effects, f_d(DOC), f_d(NO₃), and f_n(NH₄) are described by a Michaelis–Menten-like equation (Equation (96)), and they depend on substrate concentration ([S], g C m⁻³ or g N m⁻³) and on the Michaelis constant for the substrate (K_m, g C m⁻³ or g N m⁻³). The constant default values are 9.45, 16.65, and 18.53, respectively, for DOC, NO₃⁻, and NH₄⁺.

$$f\left(\left[S\right]\right)=\frac{\left[S\right]}{\left[S\right]+K_m}$$

(96)

In the STICS model [60], nitrate (NO₃, kg N ha⁻¹ cm⁻¹) concentration effect on denitrification (Equation (97)) also depends on soil bulk density (BD, g cm⁻³).

$$f_d({NO}_3)=\frac{{NO}_3}{{NO}_3+2.2·BD}$$

(97)

In the DAYCENT denitrification subroutine DSSAT model [70] V4.8.2.0 [77], a nitrate effect on the N₂/N₂O ratio (f_e(NO₃), Equation (98)) is also applied.

$$\begin{array}{l}{f}_e\left({NO}_3\right)=\left\{\begin{array}{cc}max\left(0.16·K_1,K_1·e^{\frac{-0.8·{NO}_3}{{CO}_{2correct}}} \right)\hfill & \hfill if\left[{CO}_2\right]>0.001 \\ 0.16·K_1\hfill & \hfill else\end{array}\right.\\ K_1=max\left(1.5, 38.4-350·g_{diff}\right)\end{array}$$

(98)

In the CROPSYST model [59,69,73], the response function (f_e(NO₃), Equation (99), unitless, not constrained between 0 and 1) describing NO₃ (µg N g⁻¹) effect on N₂/N₂O ratio for denitrification gas fluxes is derived from [80].

$$f_e\left({NO}_3\right)=1-\left\{0.5+\frac{1·atan\left[\pi ·0.01·\left({NO}_3-190\right)\right]}{\pi }\right\}·25$$

(99)

The response function (f_e (CO₂), Equation (100), unitless, not constrained between 0 and 1) describing soil respiration (CO_2,resp, kg C N ha⁻¹ d⁻¹) effect on N₂/N₂O ratio for denitrification gas fluxes is derived from [80].

$$f_e\left({CO}_2\right)=13+\frac{30.78·atan\left[\pi ·0.07·({CO}_{2,resp}-13)\right]}{\pi }$$

(100)

3.1.5. Model Evaluation

This section evaluates 8 (i.e., APSIM, CERES-EGC, CoupModel, DAYCENT, DNDC, EPIC, SPACSYS, and STICS) of the reviewed models, for which the model assessment of N₂O simulation performance was available in published articles. Due to limited data availability of the following models’ application and evaluation, CROPSYST, DSSAT, and ARMOSA, were not included in this section. In total, we analyzed 16 papers (

Table 2. Overview of the selected model evaluation studies analyzed in this review. The type of model evaluation is reported: calibration (CAL.) and validation (VAL.), as well as the type of environment (Env.), soil texture (Soil), Köppen climate group (Climate), and the number of treatments (n°).

Model	Ref.	Type	Country	Env.	Soil	Climate	Measure Type	n°	Measure Methodology	Simulated Emissions
APSIM	[16]	VAL.	China	Arable	Silty–loam	Cfb	Continuous fluxes field measures	3	Manual static chambers	Cumulated/ daily
	[16]	CAL.	China	Arable	Silty–loam	Cfb	Continuous fluxes field measures	1	Gas chromatography	Cumulated/ daily
CERES-EGC	[89]	VAL.	Sweden	Arable	Sandy–loam	Cfb	Not-continuous fluxes field measures	1	Manual static chambers	Daily
	[90]	VAL.	Italy	Arable	Clay–loam	Cfa	Continuous fluxes field measures	1	Automatic chambers	Daily
CoupModel	[7]	CAL.	Sweden	Lab. experiment	Silty–loam	Cfb	Not-continuos fluxes measures	16	Manual static chambers	Cumulated
	[91]	VAL.	Germany	Arable	Silty–loam	Cfb	Not-continuous fluxes field measures	3	Manual static chambers	Daily
DAYCENT	[92]	VAL.	Switzerland	Arable	Silty soil	Cfb	Not-continuous fluxes field measures	5	Manual static chambers	Cumulated
	[11]	VAL.	Colorado	Grassland	Sandy–loam, sandy–clay, clay–loam	Bsk	Not-continuous fluxes field measures	5	Automatic chambers	Cumulated/ daily
	[93]	VAL.	Colorado	Arable	Sandy–loam, clay–loam	Bsk	Not-continuous fluxes field measures	2	Automatic chambers	Cumulated
DNDC	[94]	CAL.	China	Rice/ arable	Clay–loam	Cfa	Not-continuous fluxes field measures	6	Manual static chambers	Cumulated/ daily
	[95]	VAL.	China	Rice/ arable	Silty–clay–loam	Bsk	Continuous fluxes field measures	3	Manual static chambers	Cumulated/ daily
EPIC	[96]	CAL.	USA	Arable	Silty–loam	Dfa	Not-continuous fluxes field measures	7	Manual static chambers	Cumulated/ daily
	[96]	VAL.	USA	Arable	Silty–loam	Dfa	Not-continuous fluxes field measures	7	Manual static chambers	Cumulated/ daily
	[82]	CAL.	USA	Arable	Sandy–loam	Dfa	Not-continuous fluxes field measures	6	Manual static chambers	Cumulated/ daily
SPACSYS	[71]	VAL.	Scotland	Grassland	Clay–loam	Cfb	Not-continuous fluxes field measures	3	Manual static chambers	Cumulated
	[97]	VAL.	England	Grassland	Clayey	Cfb	Not-continuous fluxes field measures	1	Manual static chambers	Cumulated
	[98]	VAL.	England	Grassland	Various	Cfb	Continuous fluxes field measures	1	Automatic chambers	Cumulated
	[97]	CAL.	England	Grassland	Clayey	Cfb	Not-continuous fluxes field measures	1	Manual static chambers	Daily
STICS	[99]	VAL.	Spain Spain–Catalogna France	Arable	Silty–clay–loam (SP), clay–loam (SP-C, FR)	Cfa (SP), Csa (SP-C), Cfb (FR)	Continuous fluxes field measures	3	Automatic chambers	Cumulated

) related to the application of these models, with 10 aimed at validation, 3 at calibration, and 3 reporting the results of both evaluation processes. The 83% of these papers were published between 2015 and 2023. In these studies, measured N₂O emissions were derived both from field and laboratory experiments conducted by the authors of the articles and from experiments carried out by other researchers. The experiment sites were categorized according to the Köppen climate classification, considering their geographical positions, to obtain an overview of the climatic conditions in which the experiments and the simulations were carried out. The most common climatic group that emerged was Cfb, corresponding to a temperature of the warmest month greater than or equal to 10 °C, and temperature of the coldest month less than 18 °C but greater than 3 °C, and precipitation evenly distributed throughout the year [88].

In more than half of the studies, measurements of N₂O emissions in the field were conducted intermittently (i.e., not-continuous measurements). Most of the studies that employed intermittent measurement approaches dealt with a large number of experimental treatments. In contrast, in studies where measurements were taken continuously, the maximum number of tested treatments was limited to 4. Simulated and measured N₂O emissions were reported by the individual studies both as cumulative and daily values. More in detail, 7 of the reviewed model evaluations used cumulated N₂O emissions, 9 used both cumulated and daily N₂O emissions, and 4 employed only daily N₂O emissions.

A comprehensive overview of the statistical indices extracted from the studies is reported in Table A9 (Appendix A.3, Appendix A), and it is organized according to the treatment(s) for which they were calculated. The most frequently reported index in the reviewed studies, determination coefficient (R²), allowed us to compare model performances concerning both cumulated and daily emissions. Other performance indices (r, RMSE, RRMSE, EF) were seldom used. Furthermore, the different time periods employed to obtain cumulated N₂O emissions values and the associated RMSE values prevented the possibility of this accuracy index comparisons, while relative errors (RRMSE) were rarely reported.

In general, the reported determination coefficient values are higher when estimated with cumulated N₂O emissions values than the ones obtained from daily values (Figure 4). When considering the combination of measure methodology (continuous and not-continuous measures) and model output (daily and cumulated emissions), differences in models’ performance are more relevant for validation studies than for calibration ones (Table A9). In the reviewed studies, the average R² obtained after calibration with continuous measures corresponds to 0.48 (with R² values reported for daily emissions ranging from 0.31 to 0.56 and from 0.30 to 0.67 for cumulated emissions), while it is equal to 0.65 for calibration studies that employed not-continuous measures (0.1–0.92 and 0.41–0.96, respectively, for daily and cumulated emissions). The average R² value, deriving from the published validation coefficient of determinations, were equal to 0.55 and 0.29, respectively, for continuous (0.05–0.74 and 0.4–0.95, respectively, for daily and cumulated emissions) and not continuous (0.02–0.5 and 0.02–0.89, respectively, for daily and cumulated emissions) measures. Frequently, models that were calibrated with continuous measures obtained higher R² when subjected to validation using the same type of measured data (particularly when the fitting index is calculated on cumulated emissions). The choice between using cumulated or daily values appears to be primarily linked to measured data frequency, which is associated with the specific research objectives and resource availability. It should be noted that the use of cumulated emissions values for model evaluation tends to reduce the disagreement between measured and simulated data, which can represent both an advantage and a disadvantage. Indeed, the use of cumulated values allows for obtaining higher determination coefficients in the calibration phase, but it does not always ensure the same results at validation (particularly when carried on independent datasets). Conversely, daily emissions values provide a more detailed view but may reveal greater discrepancies between observations and simulations (Table A9).

When considering only mineral N fertilization treatments, as expected, R² values reported in calibration studies that employed not-continuous measures (average R² 0.66) are higher than the ones obtained after calibration with continuous measures (average R² 0.48). In validation studies simulating these treatments, average R² values were, however, higher in studies that employed continuous measures (0.46) than in the ones that used not-continuous measures (0.27). Probably, this difference is due to the fact that studies that employed continuous emissions measures for validation purposes also employed model parameter sets calibrated on continuous emissions. Determination coefficients deriving from the reviewed zero N control treatments were generally low (average R² equal to 0.065 and 0.31, respectively, for continuous and not-continuous measures) since they were estimated for validation datasets of daily emissions.

4. Discussion

From the appraisal of the main approaches for N₂O emissions modeling, and in agreement with [54], it emerged that soil and weather conditions variability representation is the main driver employed for describing the interactions network that connects soil chemical–physical properties and weather conditions to soil N cycling and the consequent gaseous emissions. In the reviewed process-based models, the level of detail of weather variability representation is obtained by the adoption of a daily time step and of specific parameter values for each simulated process, thus differentiating these approaches from the statistical ones (e.g., IPPC guidelines and statistical models). Soil physical properties are adequately described by the employment of soil hydrological parameters, which allows the simulation of soil water content and temperature variations as influenced by weather trends, soil cover type (bare soil, vegetal soil cover derived from crop growth and development modules) and soil tillage operations. Differences in WFPS simulation or in soil hydrological parameters calculation arise from each model’s specific characteristics. The reviewed algorithms generally estimate nitrification and denitrification rates as potential rates limited by soil temperature and moisture response functions, both for the implicit and explicit microbial pool approaches. The main differences that lead to simulated output behaviors, specifically after calibration, are given by the formalization of response functions. Nitrification, in the majority of the approaches, is also limited by soil acidity, while denitrification in the implicit microbial pools approaches is influenced by soil respiration. Indeed, soil organic carbon pool simulation contributes to improving the quality of N₂O emissions representation in process-based models since it allows a more detailed description of the soil mineral nitrogen fluxes. When microbial biomass is explicitly simulated, nitrification and denitrification rates are directly proportional to the microbial biomass itself.

With respect to other types of modeling approaches, process-based models also allow daily representations of management operations (tillage, organic and mineral fertilization, irrigation, residue retention, or removal) and their influence on soil C and N cycles in a specific soil layer. The majority of the reviewed approaches employ dynamic assessment of the fraction of nitrified or denitrified N that is lost as N₂O, and in some cases, further emissions response functions to soil conditions are considered. The major limitation of the IPCC methodology, also shared by statistical models, is not being representative of the reality of crop and soil dynamics since environmental factors influence, and their spatial–temporal heterogeneity is not taken into account. Emission factors, produced by the application of IPCC guidelines, rely on simpler relations that assume a linear proportionality between the N mineral pool and nitrous oxide emission. While this approach is straightforward and of universal applicability, it might lead to sensible underestimation or overestimation of the total emission in case of deficiency or abundance in the N mineral pool, respectively.

Process-based approaches’ effectiveness largely depends on the quality and precision of the input data used for calibration and validation. As mentioned before [24,25,26,27,28], quantifying N₂O emissions represents a challenge, primarily due to the spatio-temporal variability of fluxes. Therefore, the chosen methodology for measuring gas fluxes plays a crucial role. Measured data uncertainty, arising, for example, from linear interpolation of manual measurements, considerably impacts the model’s performance. On the other hand, the use of automated chambers in manipulative experiments demands intensive labor, advanced sensor technology, and proficient users, while long-term unattended observations of emission fluxes and environmental driver variables by networks of permanent micrometeorological observation sites are an easy way of disposing of datasets collected in contrasting environments for calibration, validation, and comparison.

To address this uncertainty, it is necessary to increase the quantity and accuracy of measurements, even though this requires significant efforts in data collection and processing [13,50,51] and in terms of resource availability.

However, as mentioned earlier, the use of automatic systems for measures acquisition requires complex technology adoption by expert users, often presenting challenges in terms of availability and resources. When such data are available, the models can effectively represent the phenomenon accurately [43]. The current availability of long-term continuous time series of semi-hourly GHG flux data—such as ICOS Carbon Portal (https://www.icos-cp.eu/, accessed on 16 November 2023) or FLUXNET2015 dataset (https://fluxnet.org/data/fluxnet2015-dataset/, accessed on 16 November 2023)—coupled with high-quality biophysical variables as well as ancillary data and metadata represents a useful tool for carrying on multiple model comparison exercises [100]. In this regard, subsets of data might be assembled from selected permanent ecological sites of worldwide networks and be the object of relative simulation confrontation of an ensemble of models. Another consideration arises from the variable diffusivity of N₂O within the soil at different depths, making it challenging to select the appropriate simulation setup and, as a consequence, to calibrate according to measured values that are taken in the soil–atmosphere interface (usually a few centimeters depth from topsoil). This is a critical issue as the majority of selected papers do not provide information about the thickness of the topsoil layer to which the simulated emissions are referred.

One of the most used indicators of the agreement between simulated and observed data is the coefficient of determination, R². However, it is important to note that an optimal R² value (close to 1) does not necessarily guarantee the model’s ability to reproduce the processes accurately and efficiently. In the reviewed model evaluations, high R² was frequently associated with discrete RMSE values, even if the latter are reported in a few studies. In general, it is good practice to use a combination of different criteria to address model performance evaluation, adopting a broader set of indices that evaluate several aspects of model performance [101]. To truly appreciate the efforts put into measuring and modeling N₂O emissions, a set of model performance indices should be estimated for emissions and other N pools to allow a comprehensive evaluation of the modeling approaches.

5. Conclusions

In the present paper, we have undertaken a comprehensive examination of the main approaches for modeling N₂O. The modeling approaches review was based on their operational principles, although consideration was also given to the model evaluation as presented in published articles. One of the main limitations of the N₂O process-based modeling, underlined by this review, is connected to the inherent difficulties in the direct measure of emissions, which increases model evaluation process uncertainty. In particular, long-period field trials concerning representative cropping systems are required to support models’ calibration and improvement. Methodological limitations are also linked to the dynamic simulations of the other cropping system components (crop N uptake, soil organic matter pool evolution, and mineralization in particular) and their accuracy, efficiency, and robustness. This review schematically reports approaches and equations with the aim of easing the comparison of the mechanisms underlying the N₂O emissions simulation. Given the increasing interest in N₂O emissions and their environmental drivers in the agroecosystems, the application of process-based modeling to evaluate cropping system management practices constitutes a powerful tool, even with the abovementioned methodological limitations. Furthermore, process-based models allow the estimate of conditions-specific emission factors for given climate, soil, and cropping system (including annual or perennial crops) combinations that stakeholders (researchers, administrations, and farmers) can evaluate complementarily to IPCC emissions factors, thus deepening N₂O emissions dynamics assessment. Given the uncertainty associated with N₂O simulated emissions, an advisable approach is represented by multi-model ensemble applications to assess possible emissions ranges.