Flow Control around the UAS-S45 Pitching Airfoil Using a Dynamically Morphing Leading Edge (DMLE): A Numerical Study
Abstract
:1. Introduction
2. Methodology
2.1. Leading Edge Parametrization
2.2. Computational Domain and Grid Definitions
2.3. Validation of Results
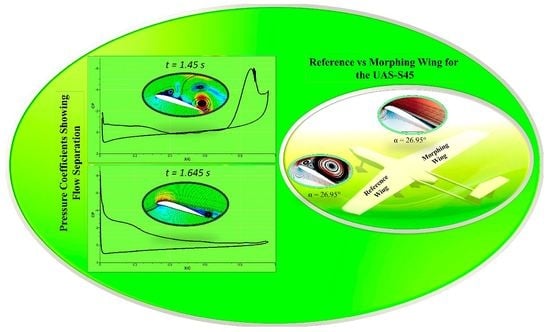
3. Discussion of Results
3.1. Results for an Oscillating Airfoil with Dynamically Morphing Leading Edge (DMLE)
3.2. Results for Dynamically Morphing Leading Edge (DMLE) of a Fixed Airfoil
4. Conclusions
- The unsteady aerodynamic parametrization method coupled with Laplace Diffusion dynamic mesh techniques gave good results. The mesh quality metrics were very well respected during the entire deformation process; hence, an accurate simulation process was confirmed by the validation of the results and mesh deformation schemes.
- For the DMLE of an oscillating airfoil, when = 0.01 and = 14.75°, the lift coefficient increased by 20.15%, while a 16.58% delay in the dynamic stall angle was obtained compared to the reference airfoil. Similarly, the lift coefficients obtained for the two other cases, when = 0.05 and = 0.0075, increased by 10.67% and 11.46%, respectively, compared to the reference airfoil.
- The presence of a LEV was depicted in the case of the reference airfoil at the angle of attack of 21.97°, also seen as a “bump” in the surface pressure distribution. By the time the angle of attack reaches 26.95°, the LEV increased and spread over the large part of the airfoil. However, in the case of the DMLE airfoils with = 0.01, 0.005, and 0075, no strong leading-edge vortex was observed for the same angles of attack of the reference airfoil.
- The numerical results have shown that the new radius of curvature of the DMLE airfoil can minimize the streamwise adverse pressure gradient, and further prevent significant flow separation by delaying the Dynamic Stall Vortex (DSV) occurrence. Furthermore, it was shown that the DMLE airfoil delayed the stall angle of attack with respect to the reference airfoil by 16.58%.
- In the case of the DMLE of an airfoil at a given angle of attack, the lift slope decreases as the leading-edge morphing begins until it reaches the maximum deflection at low deflection frequencies. When the DMLE returns to its original position, the lift slope increases again. The leading edge deflects upwards, resulting in increased flow separation and high lift slopes. The DMLE repeats the cycle, and the same trend is followed by the lift and drag coefficients of the DMLE airfoil.
- The DMLE deflects rapidly at higher frequencies, such as 5 Hz and 10 Hz, resulting in increased lift coefficients. The higher frequencies lead to more transient flow; therefore, the flow remains separated from the airfoil. In this study, the upward and downward deflection motions of DMLE airfoils have shown that the downward deflection of the DMLE increases the stall angle of attack and the nose-down pitching moment. Furthermore, the larger the downward deflection angle, the higher the lift-to-drag of the morphing wing.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Angle of attack | |
| Mean incidence angle | |
| Amplitude incidence angle | |
| Droop nose deflection | |
| Lift coefficient | |
| Maximum lift coefficient | |
| Drag coefficient | |
| Maximum drag coefficient | |
| Chord | |
| Pressure coefficient | |
| Reduced frequency | |
| Maximum value of the percentage chord line | |
| Morphing starting time | |
| Chordwise position of the maximum camber | |
| Time | |
| Freestream velocity | |
| Value of the maximum deflection of the leading edge | |
| Final y-coordinate of the new morphing airfoil camber line | |
| LEV | Leading edge vortex |
| TEV | Trailing edge vortex |
| DSV | Dynamic stall vortex |
| DMLE | Dynamically morphing leading edge |
| UDF | User-defined function |
References
- Hassanalian, M.; Abdelkefi, A. Classifications, applications, and design challenges of drones: A review. Prog. Aerosp. Sci. 2017, 91, 99–131. [Google Scholar] [CrossRef]
- Jiménez López, J.; Mulero-Pázmány, M. Drones for conservation in protected areas: Present and future. Drones 2019, 3, 10. [Google Scholar] [CrossRef] [Green Version]
- Research, P. Unmanned Aerial Vehicle (UAV) Market Size to Hit US$ 36 Bn by 2030. 7 September 2021. Available online: https://www.globenewswire.com/en/news-release/2021/09/07/2292615/0/en/Unmanned-Aerial-Vehicle-UAV-Market-Size-to-Hit-US-36-Bn-by-2030 (accessed on 18 January 2023).
- Popov, A.V.; Grigorie, L.T.; Botez, R.M.; Mamou, M.; Mébarki, Y. Real time morphing wing optimization validation using wind-tunnel tests. J. Aircr. 2010, 47, 1346–1355. [Google Scholar] [CrossRef]
- Popov, A.V.; Grigorie, T.L.; Botez, R.M.; Mébarki, Y.; Mamou, M. Modeling and testing of a morphing wing in open-loop architecture. J. Aircr. 2010, 47, 917–923. [Google Scholar] [CrossRef] [Green Version]
- Botez, R.M. Morphing wing, UAV and aircraft multidisciplinary studies at the Laboratory of Applied Research in Active Controls, Avionics and AeroServoElasticity LARCASE. Aerosp. Lab 2018, 14, 1–11. [Google Scholar]
- Hamy, A.; Murrieta-Mendoza, A.; Botez, R.M. Flight trajectory optimization to reduce fuel burn and polluting emissions using a performance database and ant colony optimization algorithm. In Proceedings of the AEGATS’16: Advanced Aircraft Efficiency in Global Air Transport System, Paris, France, 12–14 April 2016. [Google Scholar]
- Félix Patrón, R.S.; Berrou, Y.; Botez, R.M. Climb, cruise and descent 3D trajectory optimization algorithm for a flight management system. In Proceedings of the AIAA/3AF Aircraft Noise and Emissions Reduction Symposium, Atlanta, GA, USA, 16–20 June 2014; p. 3018. [Google Scholar]
- Bashir, M.; Longtin-Martel, S.; Botez, R.M.; Wong, T. Aerodynamic Design Optimization of a Morphing Leading Edge and Trailing Edge Airfoil–Application on the UAS-S45. Appl. Sci. 2021, 11, 1664. [Google Scholar] [CrossRef]
- Botez, R.M.; Koreanschi, A.; Sugar-Gabor, O.; Tondji, Y.; Guezguez, M.; Kammegne, J.; Grigorie, L.; Sandu, D.; Mebarki, Y.; Mamou, M. Numerical and experimental transition results evaluation for a morphing wing and aileron system. Aeronaut. J. 2018, 122, 747–784. [Google Scholar] [CrossRef]
- Botez, R.M. Overview of Morphing Aircraft and Unmanned Aerial Systems Methodologies and Results–Application on the Cessna Citation X, CRJ-700, UAS-S4 and UAS-S45. In Proceedings of the AIAA SCITECH 2022 Forum, San Diego, CA, USA, 3–7 January 2022; p. 1038. [Google Scholar]
- Botez, R.M.; Molaret, P.; Laurendeau, E. Laminar flow control on a research wing project presentation covering a three year period. In Proceedings of the Canadian Aeronautics and Space Institute Annual General Meeting, Toronto, ON, Canada, 30 April–2 May 2007. [Google Scholar]
- Bashir, M.; Longtin Martel, S.; Botez, R.M.; Wong, T. Aerodynamic Shape Optimization of Camber Morphing Airfoil based on Black Widow Optimization. In Proceedings of the AIAA SCITECH 2022 Forum, San Diego, CA, USA, 3–7 January 2022; p. 2575. [Google Scholar]
- Bashir, M.; Longtin Martel, S.; Botez, R.M.; Wong, T. Aerodynamic Design and Performance Optimization of Camber Adaptive Winglet for the UAS-S45. In Proceedings of the AIAA SCITECH 2022 Forum, San Diego, CA, USA, 3–7 January 2022; p. 1041. [Google Scholar]
- Bashir, M.; Longtin-Martel, S.; Botez, R.M.; Wong, T. Optimization and design of a flexible droop-nose leading-edge morphing wing based on a novel black widow optimization algorithm—Part I. Designs 2022, 6, 10. [Google Scholar] [CrossRef]
- Bashir, M.; Longtin-Martel, S.; Zonzini, N.; Botez, R.M.; Ceruti, A.; Wong, T. Optimization and Design of a Flexible Droop Nose Leading Edge Morphing Wing Based on a Novel Black Widow Optimization (BWO) Algorithm—Part II. Designs 2022, 6, 102. [Google Scholar] [CrossRef]
- Communier, D.; Le Besnerais, F.; Botez, R.M.; Wong, T. Design, manufacturing, and testing of a new concept for a morphing leading edge using a subsonic blow down wind tunnel. Biomimetics 2019, 4, 76. [Google Scholar] [CrossRef] [Green Version]
- Communier, D.; Botez, R.M.; Wong, T. Design and validation of a new morphing camber system by testing in the price—Païdoussis subsonic wind tunnel. Aerospace 2020, 7, 23. [Google Scholar] [CrossRef] [Green Version]
- Koreanschi, A.; Sugar-Gabor, O.; Ayrault, T.; Botez, R.M.; Mamou, M.; Mebarki, Y. Numerical optimization and experimental testing of a morphing wing with aileron system. In Proceedings of the 24th AIAA/AHS Adaptive Structures Conference, San Diego, CA, USA, 4–8 January 2016; p. 1083. [Google Scholar]
- Koreanschi, A.; Sugar-Gabor, O.; Botez, R.M. Drag optimisation of a wing equipped with a morphing upper surface. Aeronaut. J. 2016, 120, 473–493. [Google Scholar] [CrossRef]
- Sugar-Gabor, O.; Koreanschi, A.; Botez, R.M.; Mamou, M.; Mebarki, Y. Numerical simulation and wind tunnel tests investigation and validation of a morphing wing-tip demonstrator aerodynamic performance. Aerosp. Sci. Technol. 2016, 53, 136–153. [Google Scholar] [CrossRef] [Green Version]
- Kintscher, M.; Wiedemann, M.; Monner, H.P.; Heintze, O.; Kühn, T. Design of a smart leading edge device for low speed wind tunnel tests in the European project SADE. Int. J. Struct. Integr. 2011, 2, 383–405. [Google Scholar] [CrossRef]
- Li, Y.; Wang, X.; Zhang, D. Control strategies for aircraft airframe noise reduction. Chin. J. Aeronaut. 2013, 26, 249–260. [Google Scholar] [CrossRef] [Green Version]
- Arena, M.; Chiatto, M.; Amoroso, F.; Pecora, R.; de Luca, L. Feasibility studies for the installation of Plasma Synthetic Jet Actuators on the skin of a morphing wing flap. In Proceedings of the Active and Passive Smart Structures and Integrated Systems XII, Denver, CO, USA, 5–8 March 2018; pp. 131–139. [Google Scholar]
- Dimino, I.; Lecce, L.; Pecora, R. Morphing Wing Technologies: Large Commercial Aircraft and Civil Helicopters; Butterworth-Heinemann: Oxford, UK, 2017. [Google Scholar]
- Pecora, R. Morphing wing flaps for large civil aircraft: Evolution of a smart technology across the Clean Sky program. Chin. J. Aeronaut. 2021, 34, 13–28. [Google Scholar] [CrossRef]
- Ameduri, S.; Concilio, A.; Dimino, I.; Pecora, R.; Ricci, S. AIRGREEN2-Clean Sky 2 Programme: Adaptive Wing Technology Maturation, Challenges and Perspectives. Smart Mater. Adapt. Struct. Intell. Syst. 2018, 51944, V001T004A023. [Google Scholar]
- Giuliani, M.; Dimino, I.; Ameduri, S.; Pecora, R.; Concilio, A. Status and Perspectives of Commercial Aircraft Morphing. Biomimetics 2022, 7, 11. [Google Scholar] [CrossRef]
- Concilio, A.; Dimino, I.; Pecora, R. SARISTU: Adaptive Trailing Edge Device (ATED) design process review. Chin. J. Aeronaut. 2021, 34, 187–210. [Google Scholar] [CrossRef]
- Sugar-Gabor, O.; Simon, A.; Koreanschi, A.; Botez, R.M. Application of a morphing wing technology on hydra technologies unmanned aerial system UAS-S4. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, Montreal, QC, Canada, 14–20 November 2014; p. V001T001A037. [Google Scholar]
- Sugar-Gabor, O.; Koreanschi, A.; Botez, R.M. Analysis of UAS-S4 Éhecatl aerodynamic performance improvement using several configurations of a morphing wing technology. Aeronaut. J. 2016, 120, 1337–1364. [Google Scholar] [CrossRef]
- Olivett, A.; Corrao, P.; Karami, M.A. Flow control and separation delay in morphing wing aircraft using traveling wave actuation. Smart Mater. Struct. 2021, 30, 025028. [Google Scholar] [CrossRef]
- Katam, V.; LeBeau, R.; Jacob, J. Simulation of separation control on a morphing wing with conformal camber. In Proceedings of the 35th AIAA Fluid Dynamics Conference and Exhibit, Toronto, ON, Canada, 6–9 June 2005; p. 4880. [Google Scholar]
- Mathisen, S.; Gryte, K.; Gros, S.; Johansen, T.A. Precision deep-stall landing of fixed-wing UAVs using nonlinear model predictive control. J. Intell. Robot. Syst. 2021, 101, 1–15. [Google Scholar] [CrossRef]
- Sekimoto, S.; Kato, H.; Fujii, K.; Yoneda, H. In-Flight Demonstration of Stall Improvement Using a Plasma Actuator for a Small Unmanned Aerial Vehicle. Aerospace 2022, 9, 144. [Google Scholar] [CrossRef]
- Liiva, J. Unsteady aerodynamic and stall effects on helicopter rotor blade airfoil sections. J. Aircr. 1969, 6, 46–51. [Google Scholar] [CrossRef]
- Richez, F. Analysis of dynamic stall mechanisms in helicopter rotor environment. J. Am. Helicopter Soc. 2018, 63, 1–11. [Google Scholar] [CrossRef]
- Larsen, J.W.; Nielsen, S.R.; Krenk, S. Dynamic stall model for wind turbine airfoils. J. Fluids Struct. 2007, 23, 959–982. [Google Scholar] [CrossRef]
- Zhu, C.; Qiu, Y.; Wang, T. Dynamic stall of the wind turbine airfoil and blade undergoing pitch oscillations: A comparative study. Energy 2021, 222, 120004. [Google Scholar] [CrossRef]
- Brandon, J.M. Dynamic stall effects and applications to high performance aircraft. Aircr. Dyn. High Angl. Attack: Ezperiments Model. 1991. [Google Scholar]
- Nguyen, D.H.; Lowenberg, M.H.; Neild, S.A. Analysing dynamic deep stall recovery using a nonlinear frequency approach. Nonlinear Dyn. 2022, 108, 1179–1196. [Google Scholar] [CrossRef]
- McCroskey, W.J. The Phenomenon of Dynamic Stall; NASA: Washington, DC, USA, 1981.
- Carr, L.W. Progress in analysis and prediction of dynamic stall. J. Aircr. 1988, 25, 6–17. [Google Scholar] [CrossRef]
- Mulleners, K.; Raffel, M. Dynamic stall development. Exp. Fluids 2013, 54, 1–9. [Google Scholar] [CrossRef] [Green Version]
- McCroskey, W.J.; Carr, L.W.; McAlister, K.W. Dynamic stall experiments on oscillating airfoils. Aiaa J. 1976, 14, 57–63. [Google Scholar] [CrossRef]
- Benton, S.; Visbal, M. The onset of dynamic stall at a high, transitional Reynolds number. J. Fluid Mech. 2019, 861, 860–885. [Google Scholar] [CrossRef]
- Imamura, T.; Enomoto, S.; Yokokawa, Y.; Yamamoto, K. Three-dimensional unsteady flow computations around a conventional slat of high-lift devices. AIAA J. 2008, 46, 1045–1053. [Google Scholar] [CrossRef]
- Balaji, R.; Bramkamp, F.; Hesse, M.; Ballmann, J. Effect of flap and slat riggings on 2-D high-lift aerodynamics. J. Aircr. 2006, 43, 1259–1271. [Google Scholar] [CrossRef]
- Gerontakos, P.; Lee, T. Dynamic stall flow control via a trailing-edge flap. AIAA J. 2006, 44, 469–480. [Google Scholar] [CrossRef]
- Lee, T.; Su, Y. Unsteady airfoil with a harmonically deflected trailing-edge flap. J. Fluids Struct. 2011, 27, 1411–1424. [Google Scholar] [CrossRef]
- Traub, L.W.; Miller, A.; Rediniotis, O.; Kim, K.; Jayasuriya, S.; Jung, G. Effects of synthetic jets on large amplitude sinusoidal pitch motions. J. Aircr. 2005, 42, 282–285. [Google Scholar] [CrossRef]
- Greenblatt, D.; Wygnanski, I. Dynamic stall control by periodic excitation, Part 1: NACA 0015 parametric study. J. Aircr. 2001, 38, 430–438. [Google Scholar] [CrossRef]
- Greenblatt, D.; Wygnanski, I.J. The control of flow separation by periodic excitation. Prog. Aerosp. Sci. 2000, 36, 487–545. [Google Scholar] [CrossRef]
- Post, M.L.; Corke, T.C. Separation control using plasma actuators: Dynamic stall vortex control on oscillating airfoil. AIAA J. 2006, 44, 3125–3135. [Google Scholar] [CrossRef]
- Heine, B.; Mulleners, K.; Joubert, G.; Raffel, M. Dynamic stall control by passive disturbance generators. AIAA J. 2013, 51, 2086–2097. [Google Scholar] [CrossRef] [Green Version]
- Sahin, M.; Sankar, L.N.; Chandrasekhara, M.; Tung, C. Dynamic stall alleviation using a deformable leading edge concept-a numerical study. J. Aircr. 2003, 40, 77–85. [Google Scholar] [CrossRef] [Green Version]
- Lyu, Z.; Martins, J.R. Aerodynamic shape optimization of an adaptive morphing trailing-edge wing. J. Aircr. 2015, 52, 1951–1970. [Google Scholar] [CrossRef] [Green Version]
- Abdessemed, C.; Yao, Y.; Bouferrouk, A.; Narayan, P. Morphing airfoils analysis using dynamic meshing. Int. J. Numer. Methods Heat Fluid Flow 2018, 28, 1117–1133. [Google Scholar] [CrossRef] [Green Version]
- Kamliya Jawahar, H.; Ai, Q.; Azarpeyvand, M. Experimental and numerical investigation of aerodynamic performance of airfoils fitted with morphing trailing-edges. In Proceedings of the 23rd AIAA/CEAS Aeroacoustics Conference, Denver, CO, USA, 5–9 June 2017; p. 3371. [Google Scholar]
- Jawahar, H.K.; Ai, Q.; Azarpeyvand, M. Experimental and numerical investigation of aerodynamic performance for airfoils with morphed trailing edges. Renew. Energy 2018, 127, 355–367. [Google Scholar] [CrossRef] [Green Version]
- Le Pape, A.; Costes, M.; Richez, F.; Joubert, G.; David, F.; Deluc, J.-M. Dynamic stall control using deployable leading-edge vortex generators. AIAA J. 2012, 50, 2135–2145. [Google Scholar] [CrossRef]
- Qijun, Z.; Yiyang, M.; Guoqing, Z. Parametric analyses on dynamic stall control of rotor airfoil via synthetic jet. Chin. J. Aeronaut. 2017, 30, 1818–1834. [Google Scholar]
- Visbal, M.R.; Benton, S.I. Exploration of high-frequency control of dynamic stall using large-eddy simulations. AIAA J. 2018, 56, 2974–2991. [Google Scholar] [CrossRef]
- Visbal, M.R.; Garmann, D.J. Numerical investigation of spanwise end effects on dynamic stall of a pitching NACA 0012 wing. In Proceedings of the 55th AIAA Aerospace Sciences Meeting, Grapevine, TX, USA, 9–13 January 2017; p. 1481. [Google Scholar]
- Feszty, D.; Gillies, E.A.; Vezza, M. Alleviation of airfoil dynamic stall moments via trailing-edge flap flow control. AIAA J. 2004, 42, 17–25. [Google Scholar] [CrossRef]
- Lee, T.; Gerontakos, P. Unsteady airfoil with dynamic leading-and trailing-edge flaps. J. Aircr. 2009, 46, 1076–1081. [Google Scholar] [CrossRef]
- Gerontakos, P.; Lee, T. Trailing-edge flap control of dynamic pitching moment. AIAA J. 2007, 45, 1688–1694. [Google Scholar] [CrossRef]
- Samara, F.; Johnson, D.A. Deep dynamic stall and active aerodynamic modification on a S833 airfoil using pitching trailing edge flap. Wind Eng. 2021, 45, 884–903. [Google Scholar] [CrossRef]
- Krzysiak, A.; Narkiewicz, J. Aerodynamic loads on airfoil with trailing-edge flap pitching with different frequencies. J. Aircr. 2006, 43, 407–418. [Google Scholar] [CrossRef]
- Abdessemed, C.; Yao, Y.; Bouferrouk, A. Near Stall Unsteady Flow Responses to Morphing Flap Deflections. Fluids 2021, 6, 180. [Google Scholar] [CrossRef]
- Abdessemed, C.; Yao, Y.; Bouferrouk, A.; Narayan, P. Aerodynamic analysis of a harmonically morphing flap using a hybrid turbulence model and dynamic meshing. In Proceedings of the 2018 Applied Aerodynamics Conference, Atlanta, GA, USA, 25–29 June 2018; p. 3813. [Google Scholar]
- Abdessemed, C.; Bouferrouk, A.; Yao, Y. Aerodynamic and aeroacoustic analysis of a harmonically morphing airfoil using dynamic meshing. In Proceedings of the Acoustics, Vienna, Austria, 11–14 September 2021; pp. 177–199. [Google Scholar]
- Bangalore, A.; Sankar, L. Numerical analysis of aerodynamic performance of rotors with leading edge slats. Comput. Mech. 1996, 17, 335–342. [Google Scholar] [CrossRef]
- Geissler, W.; Sobieczky, H.; Carr, L.; Chandrasekhara, M.; Wilder, M. Compressible dynamic stall calculations incorporating transition modeling for variable geometry airfoils. In Proceedings of the 36th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 12–15 January 1998; p. 705. [Google Scholar]
- Martin, P.; McAlister, K.; Chandrasekhara, M.; Geissler, W. Dynamic Stall Measurements and Computations for a VR-12 Airfoil with a Variable Droop Leading Edge; National Aeronautics and Space Administration Moffett Field CA Rotorcraf: Mountain View, CA, USA, 2003.
- Chandrasekhara, M.; Wilder, M.; Carr, L. Unsteady stall control using dynamically deforming airfoils. AIAA J. 1998, 36, 1792–1800. [Google Scholar] [CrossRef] [Green Version]
- Lee, B.-S.; Ye, K.; Joo, W.; Lee, D.-H. Passive control of dynamic stall via nose droop with Gurney flap. In Proceedings of the 43rd AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 10–13 January 2005; p. 1364. [Google Scholar]
- Abdessemed, C.; Yao, Y.; Narayan, P.; Bouferrouk, A. Unsteady parametrization of a morphing wing design for improved aerodynamic performance. In Proceedings of the 52nd 3AF International Conference, on Applied Aerodynamics, Lyon, France, 7–29 March 2017. [Google Scholar]
- Mcallister, K.; Carr, L.; Mccroskey, W. Dynamic Stall Experiments on the NACA 0012 Airfoil; Technical report No. 1100; NASA: Washington, DC, USA, 1978.
- Correa, A.F.M. The Study of Dynamic Stall and URANS Capabilities on Modelling Pitching Airfoil Flows. Master’s Thesis, University of Federal De Uberlândia, Uberlândia, Brazil, 2015. [Google Scholar]























| Grid Size | Number of Cells | Min Length | Max Length | Bias Factor |
|---|---|---|---|---|
| 1 | 62 626 | 0.001 | 0.06 | 1.12 |
| 2 | 103 212 | 0.001 | 0.035 | 1.08 |
| 3 | 206 038 | 0.001 | 0.02 | 1.05 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bashir, M.; Zonzini, N.; Botez, R.M.; Ceruti, A.; Wong, T. Flow Control around the UAS-S45 Pitching Airfoil Using a Dynamically Morphing Leading Edge (DMLE): A Numerical Study. Biomimetics 2023, 8, 51. https://doi.org/10.3390/biomimetics8010051
Bashir M, Zonzini N, Botez RM, Ceruti A, Wong T. Flow Control around the UAS-S45 Pitching Airfoil Using a Dynamically Morphing Leading Edge (DMLE): A Numerical Study. Biomimetics. 2023; 8(1):51. https://doi.org/10.3390/biomimetics8010051
Chicago/Turabian StyleBashir, Musavir, Nicola Zonzini, Ruxandra Mihaela Botez, Alessandro Ceruti, and Tony Wong. 2023. "Flow Control around the UAS-S45 Pitching Airfoil Using a Dynamically Morphing Leading Edge (DMLE): A Numerical Study" Biomimetics 8, no. 1: 51. https://doi.org/10.3390/biomimetics8010051
APA StyleBashir, M., Zonzini, N., Botez, R. M., Ceruti, A., & Wong, T. (2023). Flow Control around the UAS-S45 Pitching Airfoil Using a Dynamically Morphing Leading Edge (DMLE): A Numerical Study. Biomimetics, 8(1), 51. https://doi.org/10.3390/biomimetics8010051