Development of a Dung Beetle Robot and Investigation of Its Dung-Rolling Behavior
Abstract
:1. Introduction
2. Materials and Methods
2.1. Observation
- The weight of the beetle can be steadily supported by the forelegs, which are short and strong.
- The ball of dung can be easily manipulated by the long mid- and hind-legs, which have spines that help to grasp the soft dung.
2.2. Robot Morphology Design
- The dung-ball was replaced by a cylinder. Due to the line contact with the ground, the rolling was close to pure rolling, and the direction could easily be kept constant.
- The forelegs were replaced by circular wheels (Figure 5). The robot had two possible foreleg ground contact points and two cylinder contact points through the other two legs. However, rolling of the cylinder was unstable because sometimes two hind-legs were not in contact with the ground, which was necessary for stability. Use of the fully-uninterrupted wheel meant that foreleg contact with the ground was continuous. In such a case, even if the other legs rolled the cylinder alternatively, the robot would always have three contact points to ensure stable body posture.
- In the early stage of robot development, ball-rolling was simplified to cylinder-rolling, and the motion projections of these two cases on the sagittal plane were indeed identical. For simulation, a model composed of two legs and one wheel was indeed a better choice. However, for empirical robotic implementation, the robot required a certain width to make its sagittal-plane forward motion feasible. In addition, one leg on the cylinder was sufficient to roll the cylinder. Thus, instead of using a middle leg and a hind leg, the robot was designed to have two hind legs and two wheels, which are leg LH/RH and LF/RF.
- Since the leg had no control over the orientation of the claw, the foot was needle-shaped with a small ball at the end to give it point contact with the simulated dung (the cylinder).
2.3. Planning the Dung Rolling Motion
- Initially, the legs were placed at the red triangles shown in Figure 9a, which are close to the starting and end points. For demonstration purposes, assume the leg placed close to the starting point is leg RH, and the other is leg LH.
- As the rolling motion starts, leg RH moves along track ①, and leg LH moves along track ③. At this stage, both hind-legs are holding the ball, so the ball rolls steadily.
- When leg RH begins moving along track ②, leg LH is lifting from the end point and moving along track ④ towards the starting point. At this stage, the ball is rolled by only one leg of this pair.
- When leg RH moves along track ③, leg LH contacts the ball at the starting point and then moves along track ①.
- Leg RH lifts from the ball after reaching the end point, and then moves back to the starting point. Leg LH keeps moving along track ② at the same time.
2.4. Experimental Validation
- The “simulated” dung: A ball was used and rolled by the robot.
- The radius of the rolling object (r): A basketball with a radius of 12.5 cm was used as the ball.
- Forward velocity (V): The forward velocity of both the robot and the ball were set at a constant 5 cm/s.
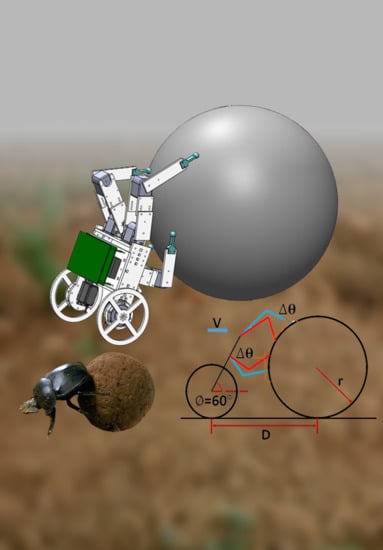
- Rolling range and the starting angle (∆θ) of the mid- and hind-legs: The rolling range was set to 30°. During the first and last 10°, the ball was rolled by four legs. During the middle 10°, the ball was rolled by two legs while the other two were in the air for repositioning.
- Body inclination (∅): when the robot rolls the ball, its body must incline on the ball to allow the mid- and hind-legs to have sufficient normal force to roll the ball. These legs also help to partially support the body weight. The body inclination was set at 60°.
- The distance between the robot body and the ball (D): This distance affects the leg trajectories. If the distance is too short, the leg trajectory may not be feasible due to tight space. In contrast, if it is too long, the ball is difficult to reach. The distance was set at 30 cm.
- Ball weight (W): we used a basketball, which weighed 650 g.
3. Results
4. Discussion
5. Conclusions and Future Work
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Saranli, U.; Buehler, M.; Koditschek, D.E. RHex: A simple and highly mobile hexapod robot. Int. J. Robot. Res. 2001, 20, 616–631. [Google Scholar] [CrossRef]
- Huang, K.J.; Huang, C.K.; Lin, P.C. A simple running model with rolling contact and its role as a template for dynamic locomotion on a hexapod robot. Bioinspir. Biomim. 2014, 9, 046004. [Google Scholar] [CrossRef] [PubMed]
- Chou, Y.C.; Yu, W.S.; Huang, K.J.; Lin, P.C. Bio-inspired step-climbing in a hexapod robot. Bioinspir. Biomim. 2012, 7, 036008. [Google Scholar] [CrossRef] [PubMed]
- Saranli, U.; Rizzi, A.A.; Koditschek, D.E. Model-based dynamic self-righting maneuvers for a hexapedal robot. Int. J. Robot. Res. 2004, 23, 903–918. [Google Scholar] [CrossRef]
- Chou, Y.C.; Huang, K.J.; Yu, W.S.; Lin, P.C. Model-based development of leaping in a hexapod robot. IEEE Trans. Robot. 2014, 31, 40–54. [Google Scholar] [CrossRef]
- Huang, K.J.; Chen, S.C.; Komsioglu, H.; Lopes, G.; Clark, J.; Lin, P.C. Design and performance evaluation of a bio-inspired and single-motor-driven hexapod robot with dynamical gaits. J. Mech. Robot. 2015, 7, 031017. [Google Scholar] [CrossRef]
- Cham, J.G.; Bailey, S.A.; Clark, J.E.; Full, R.J.; Cutkosky, M.R. Fast and robust: Hexapedal robots via shape deposition manufacturing. Int. J. Robot. Res. 2002, 21, 869–882. [Google Scholar] [CrossRef]
- Kim, S.; Clark, J.E.; Cutkosky, M.R. iSprawl: Design and tuning for high-speed autonomous open-loop running. Int. J. Robot. Res. 2006, 25, 903–912. [Google Scholar] [CrossRef]
- Szczecinski, N.S.; Chrzanowski, D.M.; Cofer, D.W.; Terrasi, A.S.; Moore, D.R.; Martin, J.P.; Ritzmann, R.E.; Quinn, R.D. Introducing MantisBot: Hexapod robot controlled by a high-fidelity, real-time neural simulation. In Proceedings of the IEEE International Conference on Intelligent Robots and Systems, Hamburg, Germany, 28 September–2 October 2015; pp. 3875–3881. [Google Scholar]
- Espenschied, K.S.; Quinn, R.D.; Chiel, H.J.; Beer, R.D. Biologically-inspired hexapod robot project: Second robot. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Nagoya, Japan, 21–27 May 1995. [Google Scholar]
- Schneider, A.; Paskarbeit, J.; Schilling, M.; Schmitz, J. HECTOR, A Bio-Inspired and Compliant Hexapod Robot; Duff, A., Prescott, T., Verschure, P., Lepora, N., Eds.; Living Machines, LNAI 8608; Springer: Cham, Switzerland, 2014; pp. 427–429. [Google Scholar]
- Paskarbeit, J.; Schilling, M.; Schmitz, J.; Schneider, A. Obstacle crossing of a real, compliant robot based on local evasion movements and averaging of stance heights using singular value decomposition. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 3140–3145. [Google Scholar]
- Von Twickel, A.; Hild, M.; Siedel, T.; Pasemann, F. Octavio: Autonomous Legs for a Reconfigurable Walking Machine; HLR 2006, French-German Workshop on Humanoid and Legged Robots; Christian Simonidis: Karlsruhe, Germany, 2006. [Google Scholar]
- Goldschmidt, D.; Hesse, F.; Worgotter, F. Biologically inspired reactive climbing behavior of hexapod robots. In Proceedings of the 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vilamoura-Algarve, Portugal, 7–12 October 2012; pp. 4632–4637. [Google Scholar]
- Microcosmos—Dung Beetle Rolls Ball and Gets Stuck. Available online: https://www.youtube.com/watch?v=AHpIlS6F2g (accessed on 13 January 2013).
- Kerem, D. Insect Leg Segments; University of Sydney: Sydney, Australia. Available online: http://bugs.bio.usyd.edu.au/learning/resources/Entomology/externalMorphology/imagePages/leg_master.html (accessed on 6 February 2018).
- Gyronotus Perissinottoi. (n.d.) in Wikipedia. Available online: https://en.wikipedia.org/wiki/Gyronotus_perissinottoi (accessed on 6 February 2018).















| Specification | Detail |
|---|---|
| Size | 450 mm × 250 mm × 120 mm |
| Mass | 1500 g |
| Body material | Acrylic (PMMA, Taipei, Taiwan) |
| Leg actuator (LM, LH, RM, RH) | Servomotor (ARS-3216HTG + HV, Alturn USA, Taichung, Taiwan) |
| Leg actuator (LF, RF) | Servomotor (MG995, Tower Pro, Taipei, Taiwan) |
| Controller | myRIO, Natinoal Instruments (Austin, TX, USA) |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.-W.; Chiang, Y.-S.; Chen, J.; Hsu, H.-H. Development of a Dung Beetle Robot and Investigation of Its Dung-Rolling Behavior. Inventions 2018, 3, 22. https://doi.org/10.3390/inventions3020022
Wang J-W, Chiang Y-S, Chen J, Hsu H-H. Development of a Dung Beetle Robot and Investigation of Its Dung-Rolling Behavior. Inventions. 2018; 3(2):22. https://doi.org/10.3390/inventions3020022
Chicago/Turabian StyleWang, Jen-Wei, Yu-Sheng Chiang, Jhih Chen, and Hao-Hsun Hsu. 2018. "Development of a Dung Beetle Robot and Investigation of Its Dung-Rolling Behavior" Inventions 3, no. 2: 22. https://doi.org/10.3390/inventions3020022
APA StyleWang, J. -W., Chiang, Y. -S., Chen, J., & Hsu, H. -H. (2018). Development of a Dung Beetle Robot and Investigation of Its Dung-Rolling Behavior. Inventions, 3(2), 22. https://doi.org/10.3390/inventions3020022