Classification and Selection of Cellular Materials in Mechanical Design: Engineering and Biomimetic Approaches
Abstract
:1. Introduction
- A Unit Cell: Most cellular materials are defined by a unit cell that is some combination of material and space. At its limit, a homogeneous material may be said to be a cellular material with a fully dense unit cell.
- Repetition: The unit cell is repeated in space to create the larger structure or surface—the resulting pattern need not be regular and may include more than one type of unit cell.
2. Engineering Approaches to Cellular Material Selection
2.1. Figures of Merit
2.2. Maxwell’s Stability Criterion
In 3D structures: M = b − 3j + 6.
- If M < 0, the structure is under-constrained
- If M = 0, the structure is a rigid framework
- If M > 0, the structure is over-constrained
2.3. Relative Density Scaling Laws
2.4. Empirical Methods
2.5. Simulation-Driven Cellular Material Design
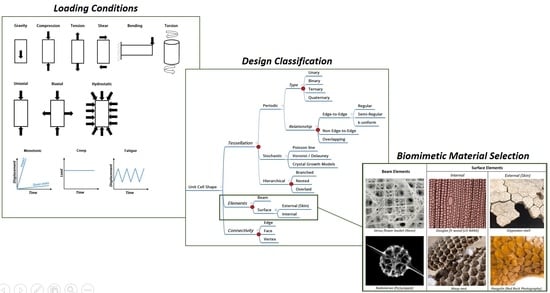
3. A New Classification of Cellular Materials
- Tessellation: The compartmentalization of space into independent volumes of a certain shape
- Elements: The use of beams and/or shells and faces within the tessellated space
- Connectivity: The actual arrangement of the elements within the tessellated space
3.1. Tessellation
3.1.1. Periodic Tessellation
3.1.2. Stochastic Tessellation
3.1.3. Hierarchical Tessellation
3.1.4. Extension to 3D
3.2. Elements
3.2.1. Beam Elements
3.2.2. Surface Elements
3.3. Connectivity
4. A Biomimetic Approach to Cellular Material Selection
4.1. Tessellation
4.1.1. Periodic Tessellation
4.1.2. Stochastic Tessellation
- The Aboav-Weaire law: The Aboav-Weaire law relates the number of edges in a particular cell to the number of edges in the cells in its neighborhood. A general observation of stochastic cellular materials in nature is that a cell with more sides than average has neighbors which, when considered together, have fewer sides than the average number. For 2-dimensional honeycombs, this relationship was first given empirically by Aboav in 1970 (with a slightly different formulation) and derived formally by Weaire in 1974 [6] is:where n is the number of edges of the candidate cell and is the average number of edges of its n neighbors (this is specific to edge-to-edge cells only). A fuller discussion of this law and its historical journey can be found in a review paper by Chiiu [69].
- The Lewis rule: F. T. Lewis studied cells in nature as a mathematical problem through the mid-1900s, publishing several papers in this field. The “Lewis rule” relates area of a cell to its number of edges [6]:where A(n) is the area of a cell with n sides, is that of the cell with average number of sides , and n0 is a constant.
4.1.3. Hierarchical Tessellation
- Murray’s law: This law, first proposed by Murray in 1926 [72], states that when a parent blood vessel branches into daughter vessels, the cube of the radius of the parent vessel is equal to the sum of the cubes of the radii of daughter blood vessels. This law has been generalized to fluidic networks of arbitrary shape and scale where for large scale channels, the ratio of the cross-sectional areas of the daughter-to-parent channels is equal to N−2/3 where N is the number of daughter channels (of constant cross-sectional shape) [73].
- Determination of Vertex angles: Thomson [74] studied the angles at the intersection of different veins and postulated that the angle was related to the “tensions” experienced in the veins. As shown in Figure 17, for a dragonfly wing, right angles (90°) are formed at the intersection of a thick, primary rib (presumably bearing more load) and a thin vein (with less load). Between these primary branches, the thin veins tend to meet at 120° angles. Recent work on dragonfly venation has added more weight to this hypothesis, with data showing a similar relationship between the interior angles in a cell and the number of primary veins it is bounded by [43].
4.2. Elements
4.3 Connectivity
4.3.1 Functional Specification
- Stiffness/rigidity (the ability to resist deformation),
- Strength (the ability to resist collapse), and
- Toughness (the ability to resist fracture)
4.3.2. Natural Models
5. Discussion
5.1. Design Methodology
- -
- Scoping: In this phase, the application context is identified and specific details of the environment (temperature, pressure, etc.) are also obtained. The functional requirements are then defined and understood to be valid in these contexts. In Figure 20, for example, a context could be aircraft paneling, where honeycomb structures are used to distribute stresses evenly.
- -
- Discovering: Following this, natural models are identified that perform these functions in similar environments—insect nests, in this example. Importantly, measurements are then made on the natural model to abstract parameters and relationships between these parameters that may, in the next step, lead to design principles.
- -
- Creating: Design principles are developed to translate the abstracted biological principle into something of use to the engineering designer, which may result in an analytical and/or numerical model that can then be exercised. In this example, the role of the corner radius is examined, and a model is developed that incorporates it.
- -
- Evaluating: In the final phase, the design principle is reconciled against other models, both in engineering and nature. We can use numerical and experimental techniques to validate our hypothesized design principle that the corner radius optimizes for specific stiffness, for example, and reconcile our findings with other insect nests and methods, such as scaling laws.
5.2. Limitations of Study
- -
- How should the density of the cellular material be prescribed within the structure? Should it be completely full of cellular materials, or are there benefits to including empty (or negative) space [83]?
- -
- How should local parameters such as thickness, beam shape be optimized? and
- -
- What is the optimum termination strategy for the cellular material at the boundary of the structure?
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ball, P. Shapes: Nature’s Patterns: A Tapestry in Three Parts; OUP Oxford: Oxford, UK, 2009. [Google Scholar]
- Schaedler, T.A.; Carter, W.B. Architected Cellular Materials. Annu. Rev. Mater. Res. 2016, 46, 187–210. [Google Scholar] [CrossRef]
- Ashby, M.F.; Evans, A.G.; Fleck, N.A.; Gibson, L.J.; Hutchinson, J.W.; Wadley, H.N.G. Metal Foams: A Design Guide; Butterworth Heinemann: Oxford, UK, 2000. [Google Scholar]
- Tashiro, T.; Ishida, A.; Hori, M.; Igisu, M.; Koike, M.; Méjean, P.; Takahata, N.; Sano, Y.; Komiya, T. Early trace of life from 3.95 Ga sedimentary rocks in Labrador, Canada. Nature 2017, 549, 516–518. [Google Scholar] [CrossRef] [PubMed]
- Varro, M.T. Rerum Rusticarum Libri III; Oxford University Press: London, UK, 1800. [Google Scholar]
- Gibson, L.J.; Ashby, M.F. Cellular Solids: Structure and Properties, 2nd ed.; Cambridge Solid State Science Series; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Gibson, L.J.; Ashby, M.F.; Harley, B.A. Cellular Materials in Nature and Medicine, 1st ed.; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- du Plessis, A.; Broeckhoven, C. Looking deep into nature: A review of micro-computed tomography in biomimicry. Acta Biomater. 2019, 85, 27–40. [Google Scholar] [CrossRef] [PubMed]
- Mcnulty, T.; Bhate, D.; Zhang, A.; Kiser, M.A.; Ferry, L.; Suder, A.; Bhattacharya, S.; Boradkar, P. A Framework for the Design of Biomimetic Cellular Materials for Additive Manufacturing. In Proceedings of the 28th Annual International Solid Freeform Fabrication Symposium, Austin, TX, USA, 7–9 August 2017; pp. 2188–2200. [Google Scholar]
- Ashby, M.F. Materials Selection in Mechanical Design, 4th ed.; Butterworth-Heinemann, Elsevier: Amsterdam, The Netherlands, 2011. [Google Scholar]
- Berger, J.B.; Wadley, H.N.G.; McMeeking, R.M. Mechanical metamaterials at the theoretical limit of isotropic elastic stiffness. Nature 2017, 543, 533–537. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Maxwell, J.C. On reciprocal figures and diagrams of forces. Philos. Mag. 1864, 4, 250–261. [Google Scholar] [CrossRef]
- Deshpande, V.S.; Ashby, M.F.; Fleck, N.A. Foam topology: Bending versus stretching dominated architectures. Acta Mater. 2001, 49, 1035–1040. [Google Scholar] [CrossRef]
- O’Masta, M.R.; Dong, L.; St-Pierre, L.; Wadley, H.N.G.; Deshpande, V.S. The fracture toughness of octet-truss lattices. J. Mech. Phys. Solids 2017, 98, 271–289. [Google Scholar] [CrossRef]
- Gümrük, R.; Mines, R.A.W. Compressive behaviour of stainless steel micro-lattice structures. Int. J. Mech. Sci. 2013, 68, 125–139. [Google Scholar] [CrossRef]
- Meza, L.R.; Phlipot, G.P.; Portela, C.M.; Maggi, A.; Montemayor, L.C.; Comella, A.; Kochmann, D.M.; Greer, J.R. Reexamining the mechanical property space of three-dimensional lattice architectures. Acta Mater. 2017, 140, 424–432. [Google Scholar] [CrossRef] [Green Version]
- Yan, C.; Hao, L.; Hussein, A.; Young, P.; Huang, J.; Zhu, W. Microstructure and mechanical properties of aluminium alloy cellular lattice structures manufactured by direct metal laser sintering. Mater. Sci. Eng. A 2015, 628, 238–246. [Google Scholar] [CrossRef]
- Yu, X.; Zhou, J.; Liang, H.; Jiang, Z.; Wu, L. Mechanical metamaterials associated with stiffness, rigidity and compressibility: A brief review. Prog. Mater. Sci. 2018, 94, 114–173. [Google Scholar] [CrossRef]
- Beyer, C.; Figueroa, D. Design and analysis of lattice structures for additive manufacturing. J. Manuf. Sci. Eng. 2016, 138, 121014. [Google Scholar] [CrossRef]
- Zhang, P.; Toman, J.; Yu, Y.; Biyikli, E.; Kirca, M.; Chmielus, M.; To, A.C. Efficient design-optimization of variable-density hexagonal cellular structure by additive manufacturing: Theory and validation. J. Manuf. Sci. Eng. 2015, 137, 021004. [Google Scholar] [CrossRef]
- NTopology. Element; NTopology: New York, NY, USA, 2018. [Google Scholar]
- Sigmund, O.; Aage, N.; Andreassen, E. On the (non-)optimality of Michell structures. Struct. Multidiscip. Optim. 2016, 54, 361–373. [Google Scholar] [CrossRef] [Green Version]
- Osanov, M.; Guest, J.K. Topology Optimization for Architected Materials Design Keywords. Annu. Rev. Mater. Res. 2016, 46, 211–233. [Google Scholar] [CrossRef]
- Cadman, J.E.; Zhou, S.; Chen, Y.; Li, Q. On design of multi-functional microstructural materials. J. Mater. Sci. 2013, 48, 51–66. [Google Scholar] [CrossRef]
- Bendsoe, M.P.; Sigmund, O. Topology Optimization: Theory, Methods and Applications; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Sigmund, O. Design of Material Structures Using Topology Optimization. Ph.D. Thesis, Technical University of Denmark, Kongens Lyngby, Denmark, 1994. [Google Scholar]
- Carstensen, J.V. Topology Optimization Algorithms for Improved Manufacturability and Cellular Material Design. Ph.D. Thesis, Johns Hopkins University, Baltimore, MD, USA, 2017. [Google Scholar]
- Cheng, L.; Liu, J.; Liang, X.; To, A.C. Coupling lattice structure topology optimization with design-dependent feature evolution for additive manufactured heat conduction design. Comput. Methods Appl. Mech. Eng. 2018, 332, 408–439. [Google Scholar] [CrossRef]
- Cheng, L.; Zhang, P.; Biyikli, E.; Bai, J.; Robbins, J.; To, A. Efficient design optimization of variable-density cellular structures for additive manufacturing: Theory and experimental validation. Rapid Prototyp. J. 2017, 23, 660–677. [Google Scholar] [CrossRef]
- Da, D.C.; Chen, J.H.; Cui, X.Y.; Li, G.Y. Design of materials using hybrid cellular automata. Struct. Multidiscip. Optim. 2017, 56, 131–137. [Google Scholar] [CrossRef]
- Basanta, D.; Bentley, P.J.; Miodownik, M.A.; Holm, E.A. Evolving Cellular Automata to Grow Microstructures. In European Conference on Genetic Programming; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Gu, G.X.; Chen, C.-T.; Richmond, D.J.; Buehler, M.J. Bioinspired hierarchical composite design using machine learning: Simulation, additive manufacturing, and experiment. Mater. Horiz. 2018, 5, 939–945. [Google Scholar] [CrossRef]
- Gu, G.X.; Chen, C.-T.; Buehler, M.J. De novo composite design based on machine learning algorithm. Extrem. Mech. Lett. 2018, 18, 19–28. [Google Scholar] [CrossRef]
- Zhang, Q.; Yang, X.; Li, P.; Huang, G.; Feng, S.; Shen, C.; Han, B.; Zhang, X.; Jin, F.; Xu, F.; et al. Bioinspired engineering of honeycomb structure—Using nature to inspire human innovation. Prog. Mater. Sci. 2015, 74, 332–400. [Google Scholar] [CrossRef]
- Ashby, M. The properties of foams and lattices. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2006, 364, 15–30. [Google Scholar] [CrossRef] [PubMed]
- Chavey, D. Tilings by Regular Polygons—II A Catalog of Tilings. Comput. Math. Applic. 1989, 17, 147–165. [Google Scholar] [CrossRef]
- Møller, J.; Stoyan, D. Stochastic Geometry and Random Tessellations. Available online: http://people.math.aau.dk/~jm/FinalJMDS.pdf (accessed on 17 March 2019).
- van Lieshout, M.N.M. An introduction to planar random tessellation models. Spat. Stat. 2012, 1, 40–49. [Google Scholar] [CrossRef] [Green Version]
- Zok, F.W.; Latture, R.M.; Begley, M.R. Periodic truss structures. J. Mech. Phys. Solids 2016, 96, 184–203. [Google Scholar] [CrossRef]
- Fazelpour, M. Developing Unit Cell Design Guidelines for Meso-Scale Periodic Cellular Materials. Ph.D. Thesis, Clemson University, Clemson, SC, USA, December 2016. [Google Scholar]
- Lenngren, N. K-Uniform Tilings By Regular Polygons. Available online: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.148.7628&rep=rep1&type=pdf (accessed on 17 March 2019).
- Grünbaum, B.; Shepard, G. Tilings by Regular Polygons. Math. Mag. 1977, 50, 227–247. [Google Scholar] [CrossRef]
- Hoffmann, J.; Donoughe, S.; Li, K.; Salcedo, M.K.; Rycroft, C.H. A simple developmental model recapitulates complex insect wing venation patterns. Proc. Natl. Acad. Sci. USA 2018, 115, 9905–9910. [Google Scholar] [CrossRef]
- Pearce, P. Structure in Nature is a Strategy for Design, 5th ed.; The MIT Press: Cambridge, MA, USA, 1990. [Google Scholar]
- Pearce, P.; Pearce, S. Polyedra Primer; Van Nostrand Reinhold Company: New York, NY, USA, 1979. [Google Scholar]
- Bhate, D. Lattice Design Optimization: Crowdsourcing Ideas in the Classroom. In Proceedings of the 29th Annual International Solid Freeform Fabrication Symposium, Austin, TX, USA, 13–15 August 2018. [Google Scholar]
- Contuzzi, N.; Campanelli, S.L.; Casavola, C.; Lamberti, L. Manufacturing and characterization of 18Ni marage 300 lattice components by selective laser melting. Materials 2013, 6, 3451–3468. [Google Scholar] [CrossRef]
- Sing, S.L.; Yeong, W.Y.; Wiria, F.E.; Tay, B.Y. Characterization of Titanium Lattice Structures Fabricated by Selective Laser Melting Using an Adapted Compressive Test Method. Exp. Mech. 2016, 56, 735–748. [Google Scholar] [CrossRef]
- Liu, J.; Gaynor, A.T.; Chen, S.; Kang, Z.; Suresh, K.; Takezawa, A.; Li, L.; Kato, J.; Tang, J.; Wang, C.C.; et al. Current and future trends in topology optimization for additive manufacturing. Struct. Multidiscip. Optim. 2018, 57, 2458–2483. [Google Scholar] [CrossRef]
- Yang, L.; Hsu, K.; Baughman, B.; Godfrey, D.; Medina, F.; Menon, M.; Wiener, S. Additive Manufacturing of Metals: The Technology, Materials, Design and Production; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Queheillalt, D.T.; Deshpande, V.S.; Wadley, H.N.G. Truss waviness effects in cellular lattice structures. J. Mech. Mater. Struct. 2007, 2, 1657–1675. [Google Scholar] [CrossRef] [Green Version]
- Han, L.; Che, S. An Overview of Materials with Triply Periodic Minimal Surfaces and Related Geometry: From Biological Structures to Self-Assembled Systems. Adv. Mater. 2018, 1705708, 1–22. [Google Scholar] [CrossRef] [PubMed]
- Schoen, A.H. Reflections concerning triply-periodic minimal surfaces. Interface Focus 2012, 2, 658–668. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- von Frisch, K. Animal Architecture (English and German Edition), 1st ed.; Harcourt: New York, NY, USA, 1974. [Google Scholar]
- Hales, T.C. The honeycomb conjecture. Discret. Comput. Geom. 2001, 25, 1–22. [Google Scholar] [CrossRef]
- Maier, M.; Hamm, C. ELISE 3D—A database-driven engineering and design tool. In Proceedings of the International Conference on Engineering Design, ICED11, Kongens Lyngby, Denmark, 15–18 August 2011. [Google Scholar]
- Seidel, R.; Lyons, K.; Blumer, M.; Zaslansky, P.; Fratzl, P.; Weaver, J.C.; Dean, M.N. Ultrastructural and developmental features of the tessellated endoskeleton of elasmobranchs (sharks and rays). J. Anat. 2016, 229, 681–702. [Google Scholar] [CrossRef]
- Fratzl, P.; Kolednik, O.; Fischer, F.D.; Dean, M.N. The mechanics of tessellations-bioinspired strategies for fracture resistance. Chem. Soc. Rev. 2016, 45, 252–267. [Google Scholar] [CrossRef]
- Du Sautoy, M. Symmetry: A Journey into the Patterns of Nature; Harper Collins: New York, NY, USA, 2008. [Google Scholar]
- Filippov, A.E.; Gorb, S.N. Modelling of the frictional behaviour of the snake skin covered by anisotropic surface nanostructures. Sci. Rep. 2016, 6, 23539. [Google Scholar] [CrossRef] [Green Version]
- Hepburn, H.R.; Pirk, C.W.W.; Duangphakdee, O. Honeybee Nests; no. 1929; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Jongerius, S.R.; Lentink, D. Structural Analysis of a Dragonfly Wing. Exp. Mech. 2010, 50, 1323–1334. [Google Scholar] [CrossRef] [Green Version]
- Dirks, J.H.; Taylor, D. Veins improve fracture toughness of insect wings. PLoS ONE 2012, 7, e43411. [Google Scholar] [CrossRef]
- Allen, M.R.; Burr, D.B. Bone Modeling and Remodeling. In Basic and Applied Bone Biology; Academic Press: Cambridge, MA, USA, 2013; pp. 75–90. [Google Scholar]
- Chintapalli, R.T.V.; Hillyer, J.F. Hemolymph circulation in insect flight appendages: Physiology of the wing heart and circulatory flow in the wings of the mosquito Anopheles gambiae. J. Exp. Biol. 2016, 219, 3945–3951. [Google Scholar] [CrossRef]
- Nielsen, D. Victoria regia’s bequest to modern architecture. Wit Trans. Ecol. Environ. 2010, 138, 65–76. [Google Scholar] [Green Version]
- Liu, X.; Dean, M.N.; Summers, A.P.; Earthman, J.C. Composite model of the shark’s skeleton in bending: A novel architecture for biomimetic design of functional compression bias. Mater. Sci. Eng. C 2010, 30, 1077–1084. [Google Scholar] [CrossRef]
- Li, R.; Bowerman, B. Symmetry breaking in biology. Cold Spring Harb. Perspect. Biol. 2010, 2, a003475. [Google Scholar] [CrossRef]
- Chiiu, S.N. Aboav-Weaire’s and Lewis’ Laws—A Review. Mater. Charact. 1995, 34, 149–165. [Google Scholar] [CrossRef]
- Combes, S.A. Flexural stiffness in insect wings I. Scaling and the influence of wing venation. J. Exp. Biol. 2003, 206, 2979–2987. [Google Scholar] [CrossRef] [Green Version]
- Kingslover, J.G.; Koehl, M.A.R. Aerodynamics, Thermoregulation, and the Evolution of Insect Wings: Differential Scaling and Evolutionary Change. Evolution 2016, 39, 488–504. [Google Scholar] [CrossRef]
- Murray, B.C.D. The Physiological Principle of Minimum Work. I. The Vascular System and the Cost of Blood Volume. Proc. Natl. Acad. Sci. USA 1926, 13, 207–214. [Google Scholar] [CrossRef]
- Stephenson, D.; Patronis, A.; Holland, D.M.; Lockerby, D.A. Generalizing Murray’s law: An optimization principle for fluidic networks of arbitrary shape and scale. J. Appl. Phys. 2016, 118, 174302. [Google Scholar] [CrossRef]
- Thompson, D.W. On Growth and Form, 1st ed.; Cambridge University Press: Cambridge, UK, 1917. [Google Scholar]
- Aizenberg, J.; Weaver, J.C.; Thanawala, M.S.; Sundar, V.C.; Morse, D.E.; Fratzl, P. Materials science: Skeleton of Euplectella sp.: Structural hierarchy from the nanoscale to the macroscale. Science 2005, 309, 275–278. [Google Scholar] [CrossRef]
- Baumeister, D. Biomimicry Resource Handbook: A Seed Bank of Best Practices; Biomimicry 3.8: Missoula, MT, USA, 2014. [Google Scholar]
- The Biomimicry Institute. Ask Nature. Available online: https://asknature.org/ (accessed on 7 May 2018).
- Seki, Y.; Kad, B.; Benson, D.; Meyers, M.A. The toucan beak: Structure and mechanical response. Mater. Sci. Eng. C 2006, 26, 1412–1420. [Google Scholar] [CrossRef]
- Fischer, S.F.; Thielen, M.; Loprang, R.R.; Seidel, R.; Fleck, C.; Speck, T.; Bührig-Polaczek, A. Pummelos as concept generators for biomimetically inspired low weight structures with excellent damping properties. Adv. Eng. Mater. 2010, 12, 658–663. [Google Scholar] [CrossRef]
- Meyers, M.A.; Chen, P.Y.; Lopez, M.I.; Seki, Y.; Lin, A.Y.M. Biological materials: A materials science approach. J. Mech. Behav. Biomed. Mater. 2011, 4, 626–657. [Google Scholar] [CrossRef]
- Lin, A.; Meyers, M.A. Growth and structure in abalone shell. Mater. Sci. Eng. A 2005, 390, 27–41. [Google Scholar] [CrossRef]
- Patek, S.N.; Korff, W.L.; Caldwell, R.L. Deadly strike mechanism of a mantis shrimp. Nature 2004, 428, 819–820. [Google Scholar] [CrossRef]
- Casanova, L.; Vijayan Anitha, V.; Kadway, N.; Gandhi, A.; Le, T.; Lee, C.; Bhate, D. On the Mechanical Behavior of Additively Manufactured Asymmetric Honeycombs. In Proceedings of the 29th Annual International Solid Freeform Fabrication Symposium, Austin, TX, USA, 13–15 August 2018. [Google Scholar]




















| Relative Density ρ*/ρs | Young’s Modulus E*/Es | Compressive Strength σ*/σs | Fracture Toughness KIc/(σs) | |
|---|---|---|---|---|
| Triangular honeycomb—out-of-plane | ||||
| Octet truss lattice |
| Packing Arrangement | Constituents | Properties |
|---|---|---|
 Screenshot from nTopology [21] | Unary system composed of a regular octahedron | One of the only regular (all faces and edges are identical), non-prismatic polyhedra that fill space by itself |
 Attr: AndrewKepert, Wikimedia | Unary system composed only of the semi-regular truncated octahedron | One of the lowest surface area per unit volume space-filling systems (but not the lowest) |
 | Binary system composed of two regular polyhedra: the octahedron and the tetrahedron | Results in the “octet” lattice structure when lattice beams are placed along each edge—a commonly used structure due to its high stiffness |
 Screenshot from nTopology [21] | Stochastic tessellation | Voronoi tessellation in 3D |
| Periodic | Stochastic | Hierarchical | |
|---|---|---|---|
| Honeybee Nest | Trabecular Bone | Dragonfly Wing Venation | |
 |  Patrick Siemer |  | |
| Mechanical | In-plane gravity loads, seasonal variation in weight [54,61] | Toughness under compressive and impact loading [7] | Flexural rigidity [62], fracture toughness [63] |
| Biological | Storage of brood, pollen and nectar; minimization of material (effort) [61] | Storage for bone marrow, nerves and blood vessels [64] | Circulation of hemolymph through wing [65] |
| Radiolarian shell Aulonia hexagona | Plant Parenchyma Helianthus (sunflower) | Amazon Water Lily Victoria amazonica | |
 Michael Spaw |  |  Laitr Keiows | |
| Mechanical | High specific strength under hydrostatic pressure and compression [56] | Maintain shape, adapt in response to environment [7] | Flexural rigidity [66] |
| Biological | Protective case, light-weight to occupy surface waters [56] | Storage of sugars, photosynthesis [7] | Carry nutrients and waste products |
| Elasmobranchii endoskeleton tesserae | Veiled Lady indusium Phallus indusiatus | Orange fruit Hesperidium | |
 Mason Dean (rights reserved), adapted from [57] |  |  | |
| Mechanical | High bending flexibility; Compressive strength [67] | Strength under variable loading (speculated) | Resilience under drop impact (speculated) |
| Biological | Space between tesserae provides room for growth [57] | Access for insects of varying sizes to fungal cap (speculated) | Improve seed dispersal (speculated) |

| Loading Conditions | Natural Model | Cellular Material Design | |||||
|---|---|---|---|---|---|---|---|
| Type | Direction | Duration | Tessellation | Elements | Connectivity | Schematic Diagram | |
| Gravity (Self-Weight) | Uniaxial | Creep | Honeybee nest  | Periodic—Unary—Edge-to-Edge—Regular | Surface | Hexagonal prism, surfaces connect edges |  |
| Compression | Hydrostatic | Dynamic, Fatigue | Venus flower basket [75]  | Hierarchical-Overlaid | Beam | Corner vertices and across faces |  |
| Bending | Variable | Dynamic | Toucan beak [78]  | Stochastic | Closed cell foam and lattice struts | Stochastically distributed faces and vertices |  |
| Bending | Distributed (surface pressure load) | Static (Stable) | Amazon waterlily leaf [66]  | Branching | Beam | Along edges defined by branching pattern |  |
| Compression | Pressure, Variable | Impact | Pummelo [79]  | Stochastic | Surface | Stochastically distributed faces |  |
| Shear | Hydrostatic | Static (Stable) | Ray [67]  | Periodic—Unary, Edge-to-Edge—Regular Hierarchical—Overlaid | Surface (tiles) | Faces |  |
| Compression | Uniaxial—Variable | Impact | Abalone shell [80,81]  | Periodic—Unary—Edge-to-Edge—Regular Hierarchical—Overlaid | Surface (tiles) | Faces |  |
| Compression | Uniaxial—Variable | Impact | Mantis shrimp [82]  | Periodic—Unary—Overlapping | Beam (fibers) | Fibers stacked along a helical twist |  |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bhate, D.; Penick, C.A.; Ferry, L.A.; Lee, C. Classification and Selection of Cellular Materials in Mechanical Design: Engineering and Biomimetic Approaches. Designs 2019, 3, 19. https://doi.org/10.3390/designs3010019
Bhate D, Penick CA, Ferry LA, Lee C. Classification and Selection of Cellular Materials in Mechanical Design: Engineering and Biomimetic Approaches. Designs. 2019; 3(1):19. https://doi.org/10.3390/designs3010019
Chicago/Turabian StyleBhate, Dhruv, Clint A. Penick, Lara A. Ferry, and Christine Lee. 2019. "Classification and Selection of Cellular Materials in Mechanical Design: Engineering and Biomimetic Approaches" Designs 3, no. 1: 19. https://doi.org/10.3390/designs3010019
APA StyleBhate, D., Penick, C. A., Ferry, L. A., & Lee, C. (2019). Classification and Selection of Cellular Materials in Mechanical Design: Engineering and Biomimetic Approaches. Designs, 3(1), 19. https://doi.org/10.3390/designs3010019