Progressive Failure Analysis of a Concrete Dam Anchored with Passive Rock Bolts
Abstract
:1. Introduction
2. Method
2.1. Analyzes
- Case 1:
- Without bolts
- Case 2:
- Bolts with a fixed attachment.
- Case 3:
- Bolts with deformable attachment.
2.2. The Dam
2.2.1. Material Properties
2.2.2. Loads
2.2.3. FE-Model
2.3. Stability Analyses of Dams
2.3.1. Analytical Stability Analyses
2.3.2. Numerical Failure Analyses
2.4. Design of Rock Bolts for Dam Stability
2.4.1. Analytical
- Cone failure in the rock
- Cone failure in the concrete
- Adhesive failure between rock and grout.
- Adhesive failure between steel and grout.
- Adhesive failure between concrete and steel.
- Steel failure.
2.4.2. Numerical Rock Bolt Model
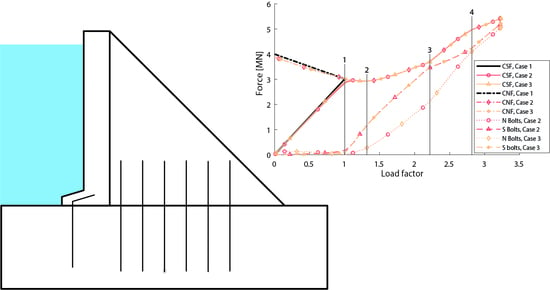
3. Results
- The failure load for Case 1, the model without bolts. From the red dashed line with triangles in Figure 6, representing the horizontal forces in the bolts in the fixed model, it can be seen that there are horizontal forces present in the bolts before this load level. This is not the case for the orange dashed line with asterisks representing the shear forces in the bolt in the Case 3 model, where the bolt forces first occur after this load level. The difference in shear force in the bolts between the Case 2 and Case 3 models is at this point approximately 100 kN.
- The initial linear slope in the force-displacement curve for Case 3 ends shortly after a minimum in the interface forces. After this point, the normal forces in the bolts are large enough to pull the dam towards the rock and create a frictional effect. The increasing load is carried by a combination of increasing forces in the concrete-rock interface and in the bolts.
- A change in failure mode occurs as the increasing load is carried by an increasing proportion by normal force in the bolts.
- Another change in behaviour of the dam, from here to the failure, is the increase in load capacity mainly due to increased forces in the bolts.
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ekström, T.; Hassanzadeh, M.; Janz, M.; Sederholm, B.; Stojanovic, B.; Ulriksen, P. Condition Assesment of Rock Anchors in Dams; Technical Report; Elforsk: Stockholm, Sweden, 2013. [Google Scholar]
- RIDAS. Swedish Hydropower Companies Guidelines for Dam Safety, Application Guideline 7.3 Concrete Dams; Technical Report; Svensk Energi: Stockholm, Sweden, 2017. [Google Scholar]
- NVE. Guidelines for Concrete Dams; Technical Report; Norges Vassdrags- og Energidirektorat: Oslo, Norway, 2005.
- Larsson, C. Investigation and Testing of Rock Bolts at Hotagen Power Station; Technical Report; Elforsk: Stockholm, Sweden, 2009. [Google Scholar]
- Hellgren, R.; Rios Bayona, F.; Malm, R.; Johansson, F. Pull-out tests of 50-year old rock bolts. In Proceedings of the International Symposium “Appropriate Technology to Ensure Proper Development, Operation and Maintenance of Dams in Developing Countries”, Johannesburg, South Africa, 18 May 2016; pp. 263–272. [Google Scholar]
- Berzell, C. Load Capacity of Grouted Rock Bolts in Concrete Dams. Master’s Thesis, KTH Royal Institute of Technology, Concrete Structures, Stockholm, Sweden, 2014. [Google Scholar]
- Westberg Wilde, M.; Johansson, F. Probabilistic Model Code for Concrete Dams; Technical Report; Energiforsk: Stockholm, Sweden, 2016. [Google Scholar]
- Malm, R.; Johansson, F.; Hellgren, R.; Ríos Bayona, F. Load Capacity of Grouted Rock Bolts Due to Degradation; Technical Report; Energiforsk: Stockholm, Sweden, 2017. [Google Scholar]
- Dassault Systemes. Abaqus CAE (version 2017) 2017. Available online: https://www.3ds.com/products-services/simulia/products/abaqus/abaquscae/ (accessed on 27 May 2019).
- Malm, R. Guideline for FE Analyses of Concrete Dams; Technical Report; Energiforsk: Stockholm, Sweden, 2016. [Google Scholar]
- Nordström, E.; Malm, R.; Johansson, F.; Ligier, P.L.; Øyvind, L. Betongdammars Brottförlopp Energiforsk Rapport 2015:122; Failure of Concrete Dams—Literature Review and Potential for Development; Technical Report; Energiforsk: Stockholm, Sweden, 2015. [Google Scholar]
- Bjurstrom, S. Shear strength of hard rock joints reinforced by grouted untensioned bolts. In Proceedings of the Third Congress of the International Society for Rock Mechanics, Denver, CO, USA, 1–7 September 1974; Volume 2, pp. 1194–1199. [Google Scholar]
- Spang, K.; Egger, P. Action of fully-grouted bolts in jointed rock and factors of influence. Rock Mech. Rock Eng. 1990, 23, 201–229. [Google Scholar] [CrossRef]
- Bjurström, S. Bolted Hard Jointed Rock; Technical Report; The Swedish Fortifications Agency: Stockholm, Sweden, 1973.
- Stille, H. Keynote Lecture: Rock Support in Theory and Practice. In Rock Support in Mining and Underground Construction; CRC Press: Boca Raton, FL, USA, 1972; pp. 421–437. [Google Scholar]
- Chen, S.H.; Qiang, S.; Chen, S.F.; Egger, P. Composite Element Model of the Fully Grouted Rock Bolt. Rock Mech. Rock Eng. 2004, 37, 193–212. [Google Scholar] [CrossRef]
- Jalalifar, H.; Aziz, N. Experimental and 3D Numerical Simulation of Reinforced Shear Joints. Rock Mech. Rock Eng. 2010, 43, 95–103. [Google Scholar] [CrossRef]
- Chen, S.H.H.; Egger, P. Three dimensional elasto-viscoplastic finite element analysis of reinforced rock masses and its application. Int. J. Numer. Anal. Methods Geomech. 1999, 23, 61–78. [Google Scholar] [CrossRef]
- Stille, H.; Holmberg, M.; Nord, G. Support of weak rock with grouted bolts and shotcrete. Int. J. Rock Mech. Min. Sci. 1989, 26, 99–113. [Google Scholar] [CrossRef]
- Chen, S.H.; Yang, Z.M.; Wang, W.M.; Shahrour, I. Study on rock bolt reinforcement for a gravity dam foundation. Rock Mech. Rock Eng. 2012, 45, 75–87. [Google Scholar] [CrossRef]
- D’Amato, M.; Braga, F.; Gigliotti, R.; Kunnath, S.; Laterza, M. Validation of a modified steel bar model incorporating bond-slip for seismic assessment of concrete structures. J. Struct. Eng. 2012, 138, 1351–1360. [Google Scholar] [CrossRef]
- Grasselli, G. 3D behaviour of bolted rock joints: Experimental and numerical study. Int. J. Rock Mech. Min. Sci. 2005, 42, 13–24. [Google Scholar] [CrossRef]
- Kilwic, A.; Yasar, E.; Celik, A.G. Effect of grout properties on the pull-out load capacity of fully grouted rock bolt. Tunn. Undergr. Space Technol. 2002, 17, 355–362. [Google Scholar] [CrossRef]
- Bahrani, N.; Hadjigeorgiou, J. Explicit reinforcement models for fully-grouted rebar rock bolts. J. Rock Mech. Geotech. Eng. 2017, 9, 267–280. [Google Scholar] [CrossRef]
- Fib. Model Code for Concrete Structures 2010; Technical Report; Wilhelm Ernst & Son: Lausanne, Switzerland, 2010. [Google Scholar]
- Sjölander, A.; Hellgren, R.; Ansell, A. Modelling aspects to predict failure of a bolt-anchored fibre reinforced shotcrete lining. In Proceedings of the Eight International Symposium on Sprayed Concrete—Modern Use of Wet Mix Sprayed Concrete for Inderground Support, Trondheim, Norway, 11–14 June 2018; pp. 278–292. [Google Scholar]
- ICOLD. Dam Failures—Statistical Analysis Bulletin 99; Technical Report; International Commission on Large Dams (ICOLD): Paris, France, 1995. [Google Scholar]






| Variable | Value | Unit |
|---|---|---|
| Density, concrete | 23 | |
| Elastic modulus, concrete | 30 | GPa |
| Density, rock mass | 26.5 | |
| Elastic modulus, rock | 30 | GPa |
| Adhesion grout-rock | 2.0 | MPa |
| Adhesion grout-steel | 1.2 | MPa |
| Adhesion concrete-steel | 3.0 | MPa |
| Elastic modulus, Steel | 200 | GPa |
| Ultimate strain, Steel, | 0.15 | - |
| Possion’s ratio, Steel | 0.30 | - |
| Yield strength, Steel | 370 | MPa |
| Ultimate strength, Steel | 600 | MPa |
| Variable | Value | Unit |
|---|---|---|
| Diameter rock bolt | 16 | mm |
| Diameter drilled hole | 32 | mm |
| Yield stress | 370 | MPa |
| Ultimate stress | 600 | MPa |
| Ultimate strain | 0.05 | - |
| Rock compressive strength | 162 | MPa |
| Rock elastic modulus | 69 | GPa |
| Friction angle along the shear plane | 31 | - |
| Applied normal stress | 4.0 | MPa |
| Model | Unit | Axial | Radial |
|---|---|---|---|
| N/mm | 120 | ||
| mm | 0 | 0 | |
| mm | 6 | 20 | |
| mm | 35 | 25 | |
| mm | 36 | 26 | |
| 0.4 | 0.8 |
| Analytic | Simulations | ||
|---|---|---|---|
| Overturning | Sliding | ||
| Case 1, without bolts | 1.35 | 1.03 | 1.00 |
| Case 2, with bolts, dowel | 2.46 | 1.73 | 3.22 |
| Case 3, with bolts, tension | 2.46 | 2.24 | 3.23 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hellgren, R.; Malm, R.; Ansell, A. Progressive Failure Analysis of a Concrete Dam Anchored with Passive Rock Bolts. Infrastructures 2020, 5, 28. https://doi.org/10.3390/infrastructures5030028
Hellgren R, Malm R, Ansell A. Progressive Failure Analysis of a Concrete Dam Anchored with Passive Rock Bolts. Infrastructures. 2020; 5(3):28. https://doi.org/10.3390/infrastructures5030028
Chicago/Turabian StyleHellgren, Rikard, Richard Malm, and Anders Ansell. 2020. "Progressive Failure Analysis of a Concrete Dam Anchored with Passive Rock Bolts" Infrastructures 5, no. 3: 28. https://doi.org/10.3390/infrastructures5030028
APA StyleHellgren, R., Malm, R., & Ansell, A. (2020). Progressive Failure Analysis of a Concrete Dam Anchored with Passive Rock Bolts. Infrastructures, 5(3), 28. https://doi.org/10.3390/infrastructures5030028