Monitoring and Modeling of Saline-Sodic Vertisol Reclamation by Echinochloa stagnina
Abstract
:1. Introduction
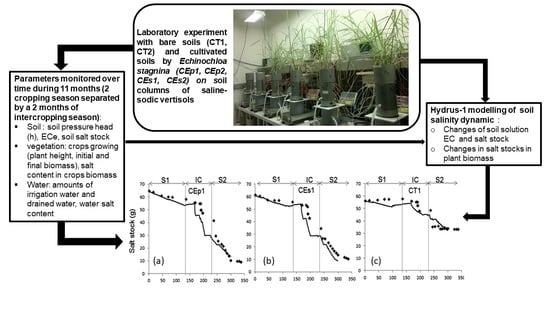
2. Materials and Methods
2.1. Soil Characteristics
2.2. Soil Column Sampling
2.3. Experimental Design
2.4. Crop Production
2.5. Soil Sampling and Soil Salinity Monitoring
2.6. Salt Accumulation in Plant Biomass and Salt Balance in the Soil
2.7. Desalinization during the Intercropping Season by Water Ponding
2.8. Modeling Approach of Vertisol Desalinization
2.8.1. General Model Description
2.8.2. Soil Hydraulic Properties
2.8.3. Numerical Simulation
2.8.4. Root Water Uptake and Salt Uptake
2.9. Statistical Analysis
3. Results
3.1. Water Flow in Soil Columns
3.2. Electrical Conductivity of the Soil Saturated Paste and in the Soil Solution
3.3. Salt Accumulation in Plant Biomass
3.4. Soil Salt Stock
3.5. Dynamics of Salt Stock during the Intercropping Season
4. Discussion
4.1. E. stagnina as a Crop for Effectively Decreasing the Salinity of Vertic Soils
4.2. Modeling of Vertisol Soil Salinity Phytoreclamation by HYDRUS-1D
4.3. Role of the Intercropping Season in the Desalinization of Vertisols
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Shrivastav, P.; Kumar, R. Soil salinity: A serious environmental issue and plant growth promoting bacteria as one of the tools for its alleviation. Saudi J. Biol. Sci. 2015, 22, 123–131. [Google Scholar] [CrossRef] [Green Version]
- Jamil, A.; Riaz, S.; Ashraf, M.; Foolad, M.R. Gene expression profiling of plants under salt stress. Crit. Rev. Plant Sci. 2011, 30, 435–458. [Google Scholar] [CrossRef]
- Balpande, S.S.; Deshpande, S.B.; Pal, D.K. Factors and processes of soil degradation in Vertisols of the Purna Valley, Maharashira, India. Land Degrad. Dev. 1996, 7, 313–324. [Google Scholar] [CrossRef]
- Adam, I.; Michot, D.; Guero, Y.; Soubega, B.; Moussa, I.; Walter, C. Detecting soil salinity changes in irrigated Vertisols by electrical resistivity prospection during a desalinization experiment. Agric. Water Manag. 2012, 109, 1–10. [Google Scholar] [CrossRef]
- Guéro, Y. Contribution à L’étude des Mécanismes de Dégradation Physico-Chimique des Sols Sous Climat Sahélien. Exemple Pris dans la Vallée du Moyen Niger. Ph.D. Thesis, Université Abdou Moumouni, Niamey, Niger, 2000; p. 109. [Google Scholar]
- Adam, I. Cartographie Fine et Suivi Détaillé de la Salinité des Sols d’un Périmètre Irrigué au Niger en Vue de Leur Remédiation. Ph.D. Thesis, Université Abdou Moumouni, Rennes, France, 2011; p. 219. [Google Scholar]
- Nouri, H.; Borujeni, S.C.; Nirola, R.; Hassanli, A.; Beecham, S.; Alaghmand, S.; Saint, C.; Mulcahy, D. Application of green remediation on soil salinity treatment: A review on halophytoremediation. Process Saf. Environ. Prot. 2017, 107, 94–107. [Google Scholar] [CrossRef]
- Qadir, M.; Ghafoor, A.; Murtaza, G. Amelioration strategies for saline soils: A review. Land Degrad. Dev. 2000, 11, 501–521. [Google Scholar] [CrossRef]
- Ravindran, K.C.; Venkatesan, K.; Balakrishnan, V.; Chellappan, K.P.; Balasubramanian, T. Restoration of saline land by halophytes for Indian soils. Soil Biol. Biochem. 2007, 39, 2661–2664. [Google Scholar] [CrossRef]
- Zorrig, W.R.M.; Ferchichi, S.; Smaoui, A.; Abdelly, C. Phytodesalination: A solution for salt-affected soils in arid and semi-arid regions. J. Arid Land Stud. 2012, 22, 299–302. [Google Scholar]
- Jesus, J.M.; Danko, A.S.; Fiúza, A.; Borges, M.T. Phytoremediation of salt-affected soils: A review of processes, applicability, and the impact of climate change. Environ. Sci. Pollut. Res. 2015, 22, 6511–6525. [Google Scholar] [CrossRef] [PubMed]
- Helalia, A.M.; El-Amir, S.; Abou-Zeid, S.T.; Zaghloul, K.F. Bio-reclamation of saline-sodic soil by Amshot grass in Northern Egypt. Soil Tillage Res. 1992, 22, 109–115. [Google Scholar] [CrossRef]
- Qadir, M.; Qureshi, R.H.; Ahmad, N.; Ilyas, M. Saline-sodic field for biomass production and soil reclamation salt-tolerant forage cultivation. Land Degrad. Dev. 1996, 7, 11–18. [Google Scholar] [CrossRef]
- Rabhi, M.; Karray-Bouraoui, N.; Medini, R.; Attia, H.; Athar, H.U.R.; Abdelly, C.; Smaoui, A. Seasonal variations in phytodesalination capacity of two perennial halophytes in their natural biotope. J. Biol. Res.-Thessalon. 2010, 14, 181–189. [Google Scholar]
- Ado, M.N.; Guéro, Y.; Michot, D.; Soubeiga, B.; Senga Kiesse, T.; Walter, C. Phytodesalinization of irrigated saline Vertisols in the Niger Valley by Echinochloa stagnina. Agric. Water Manag. 2016, 177, 229–240. [Google Scholar] [CrossRef]
- Qadir, M.; Steffens, D.; Yan, F.; Schubert, S. Sodium removal from a calcareous saline-sodic soil through leaching and plant uptake during phytoremediation. Land Degrad. Dev. 2003, 14, 301–307. [Google Scholar] [CrossRef]
- Ammari, T.G.; Tahboub, A.B.; Saoub, H.M.; Hattar, B.I.; Al-Zubi, Y.A. Salt removal efficiency as influenced by phyto-amelioration of salt-affected soils. J. Food Agric. Environ. 2008, 6, 456–460. [Google Scholar]
- Rabhi, M.; Lakhdar, A.; Hajji, S.; Barhoumi, Z.; Hamrouni, M.H.; Abdelly, C.; Smaoui, A. Evaluation of the capacity of three halophytes to desalinize their rhizosphere as grown on saline soils under nonleaching conditions. Afr. J. Ecol. 2009, 47, 463–468. [Google Scholar] [CrossRef]
- Ahmad, N.; Qureshi, R.H.; Qadir, M. Amelioration of a calcareous saline-sodic soil by gypsum and forage plants. Land Degrad. Rehabil. 1990, 2, 277–284. [Google Scholar] [CrossRef]
- Tanton, T.W.; Rycroft, D.W.; Hashimi, M. Leaching of salt from heavy clay subsoil under simulated rainfall conditions. Agric. Water Manag. 1995, 27, 321–329. [Google Scholar] [CrossRef]
- Qadir, M.; Oster, J.D.; Schubert, S.; Noble, A.D.; Sahrawat, K.L. Phytoremediation of sodic and saline-sodic soils. Adv. Agron. 2007, 96, 197–247. [Google Scholar]
- Jones, C.A. Effect of soil texture on critical bulk densities for root growth. Soil Sci. Soc. Am. J. 1983, 47, 1208–1211. [Google Scholar] [CrossRef]
- Hammecker, C.; Antonino, A.; Maeght, J.L.; Boivin, P. Experimental and numerical study of water flow in soil under irrigation in Northern Senegal: Evidence of air entrapment. Eur. J. Soil Sci. 2003, 54, 491–503. [Google Scholar] [CrossRef]
- Ndiaye, B.; Molénat, J.; Ndoye, S.; Boivin, P.; Cheverry, C.; Gascuel-Odoux, C. Modélisation du transfert de l’eau et des sels dans les casiers rizicoles du delta du fleuve Sénégal. Rev. Sci. L’Eau 2008, 21, 325–336. [Google Scholar] [CrossRef] [Green Version]
- Coppola, A.; Gerke, H.H.; Comegna, A.; Basile, A.; Comegna, V. Dual-permeability model for flow in shrinking soil with dominant horizontal deformation. Water Resour. Res. 2012, 48, 1–21. [Google Scholar] [CrossRef]
- Stewart, R.D.; Abou Najm, M.R.; Rupp, D.E.; Selker, J.S. Modeling multidomain hydraulic properties of shrink-swell soils. Water Resour. Res. 2016, 52, 7911–7930. [Google Scholar] [CrossRef]
- Wang, J.; Bai, Z.; Yang, P. Using HYDRUS to simulate the dynamic changes of Ca2+ and Na+ in sodic soils reclaimed by gypsum. Soil Water Res. 2016, 11, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Reading, L.P.; Baumgartl, T.; Bristow, K.L.; Lockington, D.A. Applying HYDRUS to flow in a sodic clay soil with solution composition–dependent hydraulic conductivity. Vadose Zone J. 2012, 11, vzj2011.0137. [Google Scholar] [CrossRef]
- Mosley, L.M.; Cook, F.; Fitzpatrick, R. Field trial modelling of different strategies for remediation of soil salinity and sodicity in lower Murray irrigation areas. Soil Res. 2017, 55, 670–681. [Google Scholar] [CrossRef]
- Barbiéro, L. Les Sols Alcalinisés sur Socle dans la Vallée du Fleuve Niger. Origines de L’Alcalinisation et Evolution des Sols Sous Irrigation. Ph.D. Thesis, ENSA de Rennes, Rennes, France, 1995. [Google Scholar]
- Léauthaud, H.C. De L’influence des Crues sur les Services Ecosystémiques des Prairies Inondables. Application à la Production Fourragère dans le Delta du Fleuve Tana, au Kenya. Ph.D. Thesis, Université de Montpellier II, Montpellier, France, 2013. [Google Scholar]
- Barbiero, L.; Valles, V.; Régeard, A.; Cheverry, C. Residual alkalinity as tracer to estimate the changes induced by forage cultivation in a non-saline irrigated sodic soil. Agric. Water Manag. 2001, 50, 229–241. [Google Scholar] [CrossRef] [Green Version]
- FAO. World Reference Base for Soil Resources: International Soil Classification System for Naming Soils and Creating Legends for Soil Maps; FAO: Rome, Italy, 2014; p. 192. [Google Scholar]
- Blackwell, P.S.; Jayawardane, N.S.; Green, T.W.; Wood, J.T.; Blackwell, J.; Beatty, H.J. Subsoil macropore space of a transitional red-brown earth after either deep tillage, gypsum or both 1. Physical effects and short-term changes. Aust. J. Soil Res. 1991, 29, 123–140. [Google Scholar] [CrossRef]
- Ado, M.N.; Michot, D.; Guero, Y.; Hallaire, V.; Dan Lamso, N.; Dutin, G.; Walter, C. Echinochloa stagnina improves soil structure and phytodesalinization of irrigated saline sodic Vertisols. Plant Soil 2019, 434, 413–424. [Google Scholar] [CrossRef]
- AFNOR. Détermination de la conductivité électrique spécifique. In Qualité des Sols, Recueil de Normes Françaises, 3rd ed.; Norme NF ISO 11265; AFNOR Editions: Paris-La, Défense, 1996; pp. 521–524. [Google Scholar]
- Slavich, P.G.; Petterson, G.H. Estimating the electrical conductivity of saturated paste extracts from 1:5 soil: Water suspensions and texture. Aust. J. Soil Res. 1993, 31, 73–81. [Google Scholar] [CrossRef]
- Paine, C.E.; Marthews, T.R.; Vogt, D.R.; Purves, D.; Rees, M.; Hector, A.; Turnbull, L.A. How to fit nonlinear plant growth models and calculate growth rates: An update for ecologists. Methods Ecol. Evol. 2012, 3, 245–256. [Google Scholar] [CrossRef]
- Chessel, D.; Dufour, A.B. Modèles Logistiques, Rapport Utilisant le Logiciel R; Université de Lyon1: Lyon, France, 2008; p. 9. [Google Scholar]
- Pinheiro, J.; Bates, D.; DebRoy, S.; Sarkar, D. Nlme: Linear and Nonlinear Mixed Effects Models, R Package Version 3; 2009; pp. 1–86. Available online: https://www.researchgate.net/publication/272475067_The_Nlme_Package_Linear_and_Nonlinear_Mixed_Effects_Models_R_Version_3 (accessed on 29 December 2021).
- Zhao, Z.Y.; Zhang, K.; Wang, P.; Wang, L.; Yin, C.H.; Tian, C.Y. The effects of halophytes on salt balance in an arid irrigation district. J. Food Agric. Environ. 2013, 11, 2669–2673. [Google Scholar]
- Simunek, J.; Sejna, M.; Saito, H.; Sakai, M.; van Genuchten, M.T. The HYDRUS-1D Software Package for Simulating the Movement of Water, Heat, and Multiple Solutes in Variably Saturated Media. Version 4.0; Hydrus Software; Department of Environmental Sciences University of California Riverside: Riverside, CA, USA, 2008; p. 315. [Google Scholar]
- Vanderboght, J.; Vereecken, H. Review of dispersivities for transport modelling in soils. Vadose Zone J. 2007, 6, 29–52. [Google Scholar] [CrossRef]
- Mualem, Y. A new model for predicting the hydraulic conductivity of unsaturated porous media. Water Resour. Res. 1976, 12, 513–522. [Google Scholar] [CrossRef] [Green Version]
- Van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef] [Green Version]
- Schaap, M.G.; Leij, F.J.; van Genuchten, M.T.; Rosetta, M.T. A computer program for estimating soil hydraulic parameters with hierarchical pedotransfer functions. J. Hydrol. 2001, 251, 163–176. [Google Scholar] [CrossRef]
- Gerke, H.H.; van Genuchten, M.T. A dual-porosity model for simulating the preferential movement of water and solutes in structured porous media. Water Resour. Res. 1993, 29, 305–319. [Google Scholar] [CrossRef]
- Skaggs, T.H.; van Genuchten, M.T.; Shouse, P.J.; Poss, J.A. Macroscopic approaches to root water uptake as a function of water and salinity stress. Agric. Water Manag. 2006, 86, 140–149. [Google Scholar] [CrossRef]
- Phogat, V.; Skewes, M.A.; Cox, J.W.; Sanderson, G.; Alam, J.; Simunek, J. Seasonal simulation of water, salinity and nitrate dynamics under drip irrigated mandarin (Citrus reticulata) and assessing management options for drainage and nitrate leaching. J. Hydrol. 2014, 513, 504–516. [Google Scholar] [CrossRef] [Green Version]
- Feddes, R.A.; Kowalik, P.J.; Zaradny, H.X. Simulation of Field Water Use and Crop Yield; Centre for Agricultural Publishing and Documentation: Wageningen, The Netherlands, 1982; pp. 194–209. [Google Scholar]
- Maas, E.V. Crop salt tolerance. In Agricultural Salinity Assessment and Management; Tanji, K.K., Ed.; ASCE Manuals and Reports on Engineering Practice, No 71; ASCE Press: New York, NY, USA, 1990. [Google Scholar]
- Simunek, J.; Hopmans, J.W. Modeling compensated root water and nutrient uptake. Ecol. Model. 2009, 220, 505–521. [Google Scholar] [CrossRef]
- Aydemir, S.; Sünger, H. Bioreclamation effect and growth of a leguminous forage plant (Lotus corniculatus) in calcareous saline-sodic soil. Afr. J. Biotechnol. 2011, 10, 15571–15577. [Google Scholar] [CrossRef]
- Yan, K.; Xu, H.; Zhao, S.; Shan, J.; Chen, X. Saline soil desalination by honeysuckle (Lonicera japonica Thunb.) depends on salt resistance mechanism. Ecol. Eng. 2016, 88, 226–231. [Google Scholar] [CrossRef]
- Garnier, P.; Perrier, E.; Bellier, G.; Rieu, M. Modelling water flow in unsaturated swelling soil samples. Bull. Soc. Geol. Fr. 1998, 169, 589–593. [Google Scholar]
- Parkhurst, D.L.; Appelo, C.A.J. Description of Input and Examples for PHREEQC Version 3: A Computer Program for Speciation, Batch-Reaction, One-Dimensional Transport, and Inverse Geochemical Calculations; U.S. Geological Survey: Menlo Park, CA, USA, 2013; p. 497. [Google Scholar]
- Kroes, J.; Van Dam, J.C.; Groenendijk, P.; Hendriks, R.F.A.; Jacobs, C.M.J. SWAP Version 3.2: Theory Description and User Manual; Alterra: Wageningen, The Netherlands, 2009; p. 262. [Google Scholar]
- Mitchell, A.R.; Ellsworth, T.R.; Meek, B.D. Effect of root systems on preferential flow in swelling soil. Commun. Soil Sci. Plant Anal. 1995, 26, 2655–2666. [Google Scholar] [CrossRef]
- Angers, D.A.; Caron, J. Plant-induced changes in soil structure: Processes and feedbacks. Biogeochemistry 1998, 42, 55–72. [Google Scholar] [CrossRef]
- Wallender, W.W.; Tanji, K.K.; Gilley, J.R.; Hill, R.W.; Lord, J.M.; Moore, C.V.; Robinson, R.R.; Stegman, E.C. Water flow and salt transport in cracking clay soils of the Imperial Valley, California. Irrig. Drain. Syst. 2006, 20, 361–387. [Google Scholar] [CrossRef]
- Favre, F.; Boivin, P.; Wopereis, M. Water movement and soil swelling in a dry, cracked Vertisols. Geoderma 1997, 78, 113–123. [Google Scholar] [CrossRef]
- Maruyama, T.; Tanji, K.K. Physical and Chemical Processes of Soil Related to Paddy Drainage; Shinzan-Sha Science and Technology: Tokyo, Japan, 1997; p. 229. [Google Scholar]
- Bouma, J. Field measurement of soil hydraulic conductivity characterizing water movement through swelling clay soils. J. Hydrol. 1980, 45, 149–158. [Google Scholar] [CrossRef]
- Greve, A.; Andersen, M.S.; Acworth, R.I. Investigations of soil cracking and preferential flow in a weighing lysimeter filled with cracking clay soil. J. Hydrol. 2010, 393, 105–113. [Google Scholar] [CrossRef]






| Clay | Silt | Sand | pH | ECe | Ca2+ | Mg2+ | Na+ | K+ | CEC | Org.C | OM | ESP b | SAR a | ESI c |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| % | dS/m | Cmol/kg | g/kg | % | ||||||||||
| 69.4 | 25.9 | 4.7 | 4.7 | 15.7 | 2.7 | 26.1 | 3.3 | 0.3 | 18.6 | 7.4 | 12.8 | 18.0 | 0.9 | 0.9 |
| CEp1 | CEp2 | CEs1 | CEs2 | CT1 | CT2 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Soil Layer (cm) | 0–19 | 19–25 | 0–19 | 19–25 | 0–19 | 19–25 | 0–19 | 19–25 | 0–19 | 19–25 | 0–19 | 19–25 | |
| Model | Parameters | ||||||||||||
| Single porosity model (S1) | (m3/m3) | 0.15 | 0.15 | 0.15 | 0.15 | 0.15 | 0.15 | 0.15 | 0.15 | 0.15 | 0.15 | 0.15 | 0.15 |
| (m3/m3) | 0.55 | 0.50 | 0.55 | 0.50 | 0.55 | 0.50 | 0.55 | 0.50 | 0.55 | 0.50 | 0.55 | 0.50 | |
| α | 0.10 | 0.10 | 0.10 | 0.10 | 0.10 | 0.10 | 0.10 | 0.10 | 0.10 | 0.10 | 0.10 | 0.10 | |
| n | 1.12 | 1.12 | 1.12 | 1.12 | 1.12 | 1.12 | 1.12 | 1.12 | 1.12 | 1.12 | 1.12 | 1.12 | |
| Ks (×10−9 m/s) | 2.3 | 1.2 | 2.3 | 1.2 | 3.5 | 1.2 | 2.3 | 1.2 | 2.3 | 1.2 | 2.3 | 1.2 | |
| Dual-porosity model (IC) | (m3/m3) | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.08 |
| (m3/m3) | 0.6 | 0.55 | 0.6 | 0.55 | 0.6 | 0.55 | 0.6 | 0.55 | 0.6 | 0.5 | 0.55 | 0.5 | |
| α | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | |
| n | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | |
| Ks (×10−9 m/s) | 81 | 17 | 12 | 8.1 | 81 | 12 | 34 | 5.8 | 23 | 8.1 | 9.3 | 1.7 | |
| Single-porosity model (S2) | (m3/m3) | 0.15 | 0.15 | 0.15 | 0.15 | 0.15 | 0.15 | 0.15 | 0.15 | 0.15 | 0.15 | 0.15 | 0.15 |
| (m3/m3) | 0.60 | 0.60 | 0.60 | 0.60 | 0.60 | 0.60 | 0.60 | 0.60 | 0.60 | 0.55 | 0.60 | 0.55 | |
| α | 0.10 | 0.10 | 0.10 | 0.10 | 0.10 | 0.10 | 0.10 | 0.10 | 0.10 | 0.10 | 0.10 | 0.10 | |
| n | 1.50 | 1.50 | 1.50 | 1.50 | 1.50 | 1.50 | 1.50 | 1.50 | 1.50 | 1.50 | 1.50 | 1.50 | |
| Ks (×10−9 m/s) | 35 | 6.9 | 23 | 2.3 | 5.8 | 35 | 35 | 5.8 | 81 | 35 | 21 | 1.2 | |
| Soil Layer | ECe | CEp1 | CEp2 | CEs1 | CEs2 | CT1 | CT2 |
|---|---|---|---|---|---|---|---|
| 0–8 cm | Initial | 13.9 | 13.9 | 13.9 | 13.9 | 13.9 | 13.9 |
| Final | 2.3 | 3.0 | 1.6 | 2.0 | 1.8 | 2.1 | |
| Reduction (%) | 84 | 79 | 88 | 85 | 87 | 85 | |
| 8–18 cm | Initial | 13.9 | 13.9 | 13.9 | 13.9 | 13.9 | 13.9 |
| Final | 3.6 | 5.9 | 2.1 | 3.9 | 3.3 | 6.8 | |
| Reduction (%) | 74 | 58 | 85 | 72 | 76 | 51 | |
| 18–25 cm | Initial | 21.2 | 17.9 | 19.4 | 16.2 | 15.3 | 17.4 |
| Final | 6.0 | 10.5 | 3.3 | 6.7 | 6.4 | 11.9 | |
| Reduction (%) | 72 | 41 | 83 | 59 | 58 | 32 |
| CEp1 | CEp2 | CEs1 | CEs2 | CT1 | CT2 | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Index | Depth | S1 | IC | S2 | S1 | IC | S2 | S1 | IC | S2 | S1 | IC | S2 | S1 | IC | S2 | S1 | IC | S2 |
| RMSE (dS/m) | 5 cm | 1.37 | 0.04 | 0.83 | 0.45 | 0.19 | 0.89 | 1.32 | 0.35 | 1.27 | 0.44 | 1.11 | 0.19 | 0.95 | 0.66 | 0.50 | 0.65 | 0.58 | 0.15 |
| 15 cm | 0.57 | 1.12 | 0.46 | 0.29 | 0.37 | 0.20 | 0.43 | 0.49 | 0.82 | 0.36 | 1.33 | 0.35 | 0.15 | 1.62 | 0.41 | 0.12 | 1.03 | 0.09 | |
| 21 cm | 2.72 | 1.45 | 0.26 | 2.07 | 1.11 | 0.38 | 0.41 | 0.74 | 0.82 | 1.52 | 1.60 | 0.26 | 2.32 | 1.87 | 0.28 | 1.25 | 1.19 | 0.18 | |
| NSE | 5 cm | 0.29 | 0.99 | 0.37 | 0.93 | 0.99 | 0.44 | 0.21 | 0.99 | 0.35 | 0.42 | 0.97 | 0.59 | 0.82 | 0.98 | 0.99 | 0.81 | 0.98 | 0.80 |
| 15 cm | 0.51 | 0.96 | 0.92 | 0.94 | 0.98 | 0.96 | 0.77 | 0.99 | 0.88 | 0.47 | 0.93 | 0.96 | 0.14 | 0.90 | 0.79 | 0.01 | 0.89 | 0.98 | |
| 21 cm | 0.45 | 0.95 | 0.98 | 0.55 | 0.91 | 0.89 | 0.98 | 0.99 | 0.91 | 0.99 | 0.89 | 0.98 | 0.35 | 0.90 | 0.93 | 0.99 | 0.87 | 0.94 | |
| Component | CEp1 | CEp2 | CEs1 | CEs2 | CT1 | CT2 |
|---|---|---|---|---|---|---|
| SSi | 64.5 | 59.0 | 61.3 | 57.2 | 56.2 | 58.3 |
| SSe | 7.6 | 7.9 | 7.7 | 7.1 | 4.4 | 3.4 |
| SSf | 9.2 | 20.3 | 10.4 | 22.2 | 33.1 | 40.5 |
| ∆SS | 63.0 | 46.6 | 58.7 | 42.1 | 27.4 | 21.2 |
| Desalinization % | 87 | 70 | 85 | 65 | 45 | 34 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ado, M.N.; Michot, D.; Guero, Y.; Thomas, Z.; Walter, C. Monitoring and Modeling of Saline-Sodic Vertisol Reclamation by Echinochloa stagnina. Soil Syst. 2022, 6, 4. https://doi.org/10.3390/soilsystems6010004
Ado MN, Michot D, Guero Y, Thomas Z, Walter C. Monitoring and Modeling of Saline-Sodic Vertisol Reclamation by Echinochloa stagnina. Soil Systems. 2022; 6(1):4. https://doi.org/10.3390/soilsystems6010004
Chicago/Turabian StyleAdo, Maman Nassirou, Didier Michot, Yadji Guero, Zahra Thomas, and Christian Walter. 2022. "Monitoring and Modeling of Saline-Sodic Vertisol Reclamation by Echinochloa stagnina" Soil Systems 6, no. 1: 4. https://doi.org/10.3390/soilsystems6010004
APA StyleAdo, M. N., Michot, D., Guero, Y., Thomas, Z., & Walter, C. (2022). Monitoring and Modeling of Saline-Sodic Vertisol Reclamation by Echinochloa stagnina. Soil Systems, 6(1), 4. https://doi.org/10.3390/soilsystems6010004