Raman Activities of Cyano-Ester Quinoidal Oligothiophenes Reveal Their Diradical Character and the Proximity of the Low-Lying Double Exciton State
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Details
2.2. Computational Details
3. Results and Discussion
3.1. The Library of Ground State Geometries and Their Associated Diradical Character
3.2. Absorption Spectra and Low-Lying Excited Electronic States
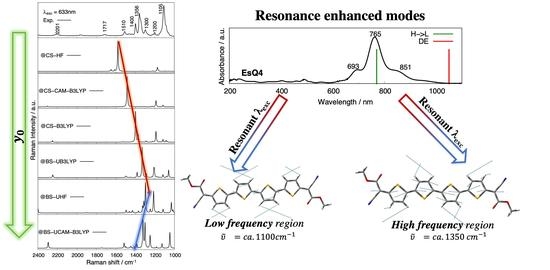
3.3. Experimental and Simulated Raman Spectra
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Huang, Y.; Egap, E. Open-shell organic semiconductors: An emerging class of materials with novel properties. Polym. J. 2018, 50, 603–614. [Google Scholar] [CrossRef]
- Hu, X.; Wang, W.; Wang, D.; Zheng, Y. The electronic applications of stable diradicaloids: Present and future. J. Mater. Chem. C 2018, 6, 11232–11242. [Google Scholar] [CrossRef]
- Chen, Z.X.; Li, Y.; Huang, F. Persistent and Stable Organic Radicals: Design, Synthesis and Applications. Chem 2021, 7, 288–332. [Google Scholar] [CrossRef]
- Dong, S.; Li, Z. Recent progress in open-shell organic conjugated materials and their aggregated states. J. Mater. Chem. C 2022, 10, 2431–2449. [Google Scholar] [CrossRef]
- Abe, M. Diradicals. Chem. Rev. 2013, 113, 7011–7088. [Google Scholar] [CrossRef] [PubMed]
- Ponce Ortiz, R.; Casado, J.; Hernández, V.; López Navarrete, J.T.; Ortí, E.; Viruela, P.M.; Milián, B.; Hotta, S.; Zotti, G.; Zecchin, S.; et al. Magnetic properties of quinoidal oligothiophenes: More than good candidates for ambipolar organic semiconductors? Adv. Funct. Mater. 2006, 16, 531–536. [Google Scholar] [CrossRef]
- Pappenfus, T.M.; Chesterfield, R.J.; Frisbie, C.D.; Mann, K.R.; Casado, J.; Raff, J.D.; Miller, L.L. A π-Stacking Terthiophene-Based Quinodimethane Is an n-Channel Conductor in a Thin Film Transistor. J. Am. Chem. Soc. 2002, 124, 4184–4185. [Google Scholar] [CrossRef]
- Janzen, D.E.; Burand, M.W.; Ewbank, P.C.; Pappenfus, T.M.; Higuchi, H.; da Silva Filho, D.A.; Young, V.G.; Brédas, J.-L.; Mann, K.R. Preparation and Characterization of π-Stacking Quinodimethane Oligothiophenes. Predicting Semiconductor Behavior and Bandwidths from Crystal Structures and Molecular Orbital Calculations. J. Am. Chem. Soc. 2004, 126, 15295–15308. [Google Scholar] [CrossRef]
- Kunugi, Y.; Takimiya, K.; Toyoshima, Y.; Yamashita, K.; Aso, Y.; Otsubo, T. Vapour deposited films of quinoidal biselenophene and bithiophene derivatives as active layers of n-channel organic field-effect transistors. J. Mater. Chem. 2004, 14, 1367. [Google Scholar] [CrossRef]
- Takahashi, T.; Matsuoka, K.-I.; Takimiya, K.; Otsubo, T.; Aso, Y. Extensive Quinoidal Oligothiophenes with Dicyanomethylene Groups at Terminal Positions as Highly Amphoteric Redox Molecules. J. Am. Chem. Soc. 2005, 127, 8928–8929. [Google Scholar] [CrossRef]
- Handa, S.; Miyazaki, E.; Takimiya, K.; Kunugi, Y. Solution-Processible n-Channel Organic Field-Effect Transistors Based on Dicyanomethylene-Substituted Terthienoquinoid Derivative. J. Am. Chem. Soc. 2007, 129, 11684–11685. [Google Scholar] [CrossRef] [PubMed]
- Ribierre, J.C.; Fujihara, T.; Watanabe, S.; Matsumoto, M.; Muto, T.; Nakao, A.; Aoyama, T. Direct Laser Writing of Complementary Logic Gates and Lateral p-n Diodes in a Solution-Processible Monolithic Organic Semiconductor. Adv. Mater. 2010, 22, 1722–1726. [Google Scholar] [CrossRef] [PubMed]
- Yamamoto, K.; Ie, Y.; Nitani, M.; Tohnai, N.; Kakiuchi, F.; Zhang, K.; Pisula, W.; Asadi, K.; Blom, P.W.M.; Aso, Y. Oligothiophene quinoids containing a benzo[c]thiophene unit for the stabilization of the quinoidal electronic structure. J. Mater. Chem. C 2018, 6, 7493–7500. [Google Scholar] [CrossRef] [Green Version]
- Yamamoto, K.; Kato, S.; Zajaczkowska, H.; Marszalek, T.; Blom, P.W.M.; Ie, Y. Effects of fluorine substitution in quinoidal oligothiophenes for use as organic semiconductors. J. Mater. Chem. C 2020, 8, 3580–3588. [Google Scholar] [CrossRef]
- Moles Quintero, S.; Zafra, J.L.; Yamamoto, K.; Aso, Y.; Ie, Y.; Casado, J. Oligoene and cyanine features of tetracyano quinoidal oligothiophenes. J. Mater. Chem. C 2021, 9, 10727–10740. [Google Scholar] [CrossRef]
- Casado, J.; Miller, L.L.; Mann, K.R.; Pappenfus, T.M.; Higuchi, H.; Ortí, E.; Milián, B.; Pou-Amérigo, R.; Hernández, V.; López Navarrete, J.T. Quinonoid Oligothiophenes as Electron-Donor and Electron-Acceptor Materials. A Spectroelectrochemical and Theoretical Study. J. Am. Chem. Soc. 2002, 124, 12380–12388. [Google Scholar] [CrossRef]
- Ponce Ortiz, R.; Casado, J.; Rodríguez González, S.; Hernández, V.; López Navarrete, J.T.; Viruela, P.M.; Ortí, E.; Takimiya, K.; Otsubo, T. Quinoidal oligothiophenes: Towards biradical ground-state species. Chem.—A Eur. J. 2010, 16, 470–484. [Google Scholar] [CrossRef] [PubMed]
- Casado, J.; Hernández, V.; López Navarrete, J.T. Vibrational Raman Shifts and Aromaticity: The Case of Oligothiophenes. Chem. Rec. 2015, 15, 1110–1118. [Google Scholar] [CrossRef]
- Casado, J. Para-Quinodimethanes: A Unified Review of the Quinoidal-Versus-Aromatic Competition and its Implications. Top. Curr. Chem. 2017, 375, 73. [Google Scholar] [CrossRef]
- Ponce Ortiz, R.; Casado, J.; Hernández, V.; López Navarrete, J.T.; Viruela, P.M.; Ortí, E.; Takimiya, K.; Otsubo, T. On the biradicaloid nature of long quinoidal oligothiophenes: Experimental evidence guided by theoretical studies. Angew. Chem. Int. Ed. 2007, 46, 9057–9061. [Google Scholar] [CrossRef]
- Casado, J.; Ponce Ortiz, R.; López Navarrete, J.T. Quinoidal oligothiophenes: New properties behind an unconventional electronic structure. Chem. Soc. Rev. 2012, 41, 5672–5686. [Google Scholar] [CrossRef] [PubMed]
- Fazzi, D.; Canesi, E.V.; Negri, F.; Bertarelli, C.; Castiglioni, C. Biradicaloid Character of Thiophene-Based Heterophenoquinones: The Role of Electron–Phonon Coupling. ChemPhysChem 2010, 11, 3685–3695. [Google Scholar] [CrossRef] [PubMed]
- Casado, J.; López Navarrete, J.T. The longest quinoidal oligothiophene: A Raman story. Chem. Rec. 2011, 11, 45–53. [Google Scholar] [CrossRef] [PubMed]
- Castiglioni, C.; López Navarrete, J.T.; Zerbi, G.; Gussoni, M. A simple interpretation of the vibrational spectra of undoped, doped and photoexcited polyacetylene: Amplitude mode theory in the GF formalism. Solid State Commun. 1988, 65, 625–630. [Google Scholar] [CrossRef]
- Zerbi, G.; Castiglioni, C.; López Navarrete, J.T.; Bogang, T.; Gussoni, M. A molecular viewpoint of lattice dynamics and spectra of conducting polymers. Synth. Met. 1989, 28, D359–D368. [Google Scholar] [CrossRef]
- Castiglioni, C.; Tommasini, M.; Zerbi, G. Raman spectroscopy of polyconjugated molecules and materials: Confinement effect in one and two dimensions. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2004, 362, 2425–2459. [Google Scholar] [CrossRef]
- Zerbetto, F.; Zgierski, M.Z.; Negri, F.; Orlandi, G. Theoretical study of the force fields of the three lowest singlet electronic states of linear polyenes. J. Chem. Phys. 1988, 89, 3681–3688. [Google Scholar] [CrossRef]
- Negri, F.; Orlandi, G.; Zerbetto, F.; Zgierski, M.Z. Theoretical study of the force field of the lowest singlet electronic states of long polyenes. J. Chem. Phys. 1989, 91, 6215–6224. [Google Scholar] [CrossRef]
- Negri, F.; Zgierski, M.Z. The vibronic structure of the S0 <-> S1 and S0 <-> S2 transitions in simple oligomers of thiophene. J. Chem. Phys. 1994, 100, 2571–2587. [Google Scholar] [CrossRef]
- Medina Rivero, S.; Canola, S.; Zeng, W.; Ramírez, F.J.; Zafra, J.L.; Wu, J.; Negri, F.; Casado, J. Long rylene nanoribbons express polyacetylene-like signatures at their edges. Phys. Chem. Chem. Phys. 2019, 21, 7281–7287. [Google Scholar] [CrossRef]
- González-Cano, R.C.; Di Motta, S.; Zhu, X.; López Navarrete, J.T.; Tsuji, H.; Nakamura, E.; Negri, F.; Casado, J. Carbon-Bridged Phenylene-Vinylenes: On the Common Diradicaloid Origin of Their Photonic and Chemical Properties. J. Phys. Chem. C 2017, 121, 23141–23148. [Google Scholar] [CrossRef]
- Lahti, P.M.; Ichimura, A.S.; Sanborn, J.A. Methodologies for Computational Studies of Quininoidal Diiminediyls: Biradical vs Dinitrene Behavior. J. Phys. Chem. A 2001, 105, 251–260. [Google Scholar] [CrossRef]
- Albrecht, A.C. On the Theory of Raman Intensities. J. Chem. Phys. 1961, 34, 1476–1484. [Google Scholar] [CrossRef]
- Guthmuller, J. Comparison of simplified sum-over-state expressions to calculate resonance Raman intensities including Franck-Condon and Herzberg-Teller effects. J. Chem. Phys. 2016, 144, 064106. [Google Scholar] [CrossRef]
- Guthmuller, J. The role of Herzberg-Teller effects on the resonance Raman spectrum of trans -porphycene investigated by time dependent density functional theory. J. Chem. Phys. 2018, 148, 124107. [Google Scholar] [CrossRef]
- Michl, J.; Bonačić-Koutecký, V. Biradicals and biradicaloids: A unified view. Tetrahedron 1988, 44, 7559–7585. [Google Scholar] [CrossRef]
- Canola, S.; Casado, J.; Negri, F. The double exciton state of conjugated chromophores with strong diradical character: Insights from TDDFT calculations. Phys. Chem. Chem. Phys. 2018, 20, 24227–24238. [Google Scholar] [CrossRef]
- Canola, S.; Dai, Y.; Negri, F. The Low Lying Double-Exciton State of Conjugated Diradicals: Assessment of TDUDFT and Spin-Flip TDDFT Predictions. Computation 2019, 7, 68. [Google Scholar] [CrossRef] [Green Version]
- Negri, F.; Canola, S.; Dai, Y. Spectroscopy of Open-Shell Singlet Ground-State Diradicaloids: A Computational Perspective. In Diradicaloids; Wu, J., Ed.; Jenny Stanford Publishing: New York, NY, USA, 2022; pp. 145–179. ISBN 978-981-4968-08-9. [Google Scholar]
- Suzuki, Y.; Miyazaki, E.; Takimiya, K. ((Alkyloxy)carbonyl)cyanomethylene-substituted thienoquinoidal compounds: A New class of soluble n-channel organic semiconductors for air-stable organic field-effect transistors. J. Am. Chem. Soc. 2010, 132, 10453–10466. [Google Scholar] [CrossRef]
- Thorley, K.J.; McCulloch, I. Why are S-F and S-O non-covalent interactions stabilising? J. Mater. Chem. C 2018, 6, 12413–12421. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Marian, C.M.; Heil, A.; Kleinschmidt, M. The DFT/MRCI method. WIREs Comput. Mol. Sci. 2019, 9, 1–31. [Google Scholar] [CrossRef] [Green Version]
- Yamaguchi, K. The electronic structures of biradicals in the unrestricted Hartree-Fock approximation. Chem. Phys. Lett. 1975, 33, 330–335. [Google Scholar] [CrossRef]
- Neese, F.; Wennmohs, F.; Becker, U.; Riplinger, C. The ORCA quantum chemistry program package. J. Chem. Phys. 2020, 152, 224108. [Google Scholar] [CrossRef] [PubMed]
- Malagoli, M.; Coropceanu, V.; Da Silva Filho, D.A.; Brédas, J.L. A multimode analysis of the gas-phase photoelectron spectra in oligoacenes. J. Chem. Phys. 2004, 120, 7490–7496. [Google Scholar] [CrossRef] [Green Version]
- Negri, F.; Zgierski, M.Z. Franck-Condon analysis of the S0→T1 absorption and phosphorescence spectra of biphenyl and bridged derivatives. J. Chem. Phys. 1992, 97, 7124–7136. [Google Scholar] [CrossRef]
- Di Motta, S.; Negri, F.; Fazzi, D.; Castiglioni, C.; Canesi, E.V. Biradicaloid and Polyenic Character of Quinoidal Oligothiophenes Revealed by the Presence of a Low-Lying Double-Exciton State. J. Phys. Chem. Lett. 2010, 1, 3334–3339. [Google Scholar] [CrossRef]
- Di Donato, E.; Vanzo, D.; Semeraro, M.; Credi, A.; Negri, F. Tuning Fluorescence Lifetimes through Changes in Herzberg−Teller Activities: The Case of Triphenylene and Its Hexamethoxy-Substituted Derivative. J. Phys. Chem. A 2009, 113, 6504–6510. [Google Scholar] [CrossRef]
- Guthmuller, J.; Champagne, B. Resonance Raman scattering of rhodamine 6G as calculated by time-dependent density functional theory: Vibronic and solvent effects. J. Phys. Chem. A 2008, 112, 3215–3223. [Google Scholar] [CrossRef]









| Geometry → | CS-HF | CS- CAM-B3LYP | CS-B3LYP | BS-UB3LYP | BS- UCAM-B3LYP | BS-UHF |
|---|---|---|---|---|---|---|
| Molecule ↓ | ||||||
| EsQ2 | 0.14 | 0.21 | 0.27 | / | / | 0.39 |
| EsQ3 | 0.22 | 0.31 | 0.41 | / | 0.50 | 0.56 |
| EsQ4 | 0.28 | 0.42 | 0.54 | 0.64 | 0.73 | 0.69 |
| Molecule ↓ | Excited Electronic State | Calc (eV) | Calc (nm) | Exp (nm) |
|---|---|---|---|---|
| EsQ2 | H→L | 2.29 | 541 | 550 |
| DE | 2.45 | 506 | - | |
| EsQ3 | DE | 1.67 | 740 | 750 * |
| H→L | 1.88 | 659 | 640 | |
| EsQ4 | DE | 1.18 | 1050 | 1050 * |
| H→L | 1.61 | 770 | 765 |
| EsQ2 | EsQ3 | EsQ4 | |||
|---|---|---|---|---|---|
| Frequency/cm−1 | HR Factor a | Frequency/cm−1 | HR Factor a | Frequency/cm−1 | HR Factor b |
| 1118 | 0.0349 | 1096 | 0.0130 | 1046 | 0.0750 |
| 1198 | 0.0263 | 1120 | 0.0196 | 1249 | 0.0591 |
| 1229 | 0.0874 | 1203 | 0.0755 | 1301 | 0.0400 |
| 1296 | 0.0199 | 1225 | 0.0278 | 1316 | 0.0162 |
| 1495 | 0.2029 | 1447 | 0.1443 | 1322 | 0.1112 |
| 1527 | 0.0367 | 1447 | 0.0595 | 1385 | 0.0104 |
| 1499 | 0.0017 | ||||
| 1516 | 0.0029 | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dai, Y.; Bonometti, L.; Zafra, J.L.; Takimiya, K.; Casado, J.; Negri, F. Raman Activities of Cyano-Ester Quinoidal Oligothiophenes Reveal Their Diradical Character and the Proximity of the Low-Lying Double Exciton State. Chemistry 2022, 4, 329-344. https://doi.org/10.3390/chemistry4020025
Dai Y, Bonometti L, Zafra JL, Takimiya K, Casado J, Negri F. Raman Activities of Cyano-Ester Quinoidal Oligothiophenes Reveal Their Diradical Character and the Proximity of the Low-Lying Double Exciton State. Chemistry. 2022; 4(2):329-344. https://doi.org/10.3390/chemistry4020025
Chicago/Turabian StyleDai, Yasi, Laura Bonometti, José Luis Zafra, Kazuo Takimiya, Juan Casado, and Fabrizia Negri. 2022. "Raman Activities of Cyano-Ester Quinoidal Oligothiophenes Reveal Their Diradical Character and the Proximity of the Low-Lying Double Exciton State" Chemistry 4, no. 2: 329-344. https://doi.org/10.3390/chemistry4020025
APA StyleDai, Y., Bonometti, L., Zafra, J. L., Takimiya, K., Casado, J., & Negri, F. (2022). Raman Activities of Cyano-Ester Quinoidal Oligothiophenes Reveal Their Diradical Character and the Proximity of the Low-Lying Double Exciton State. Chemistry, 4(2), 329-344. https://doi.org/10.3390/chemistry4020025