A Simulation and Empirical Study of Differential Test Functioning (DTF)
Abstract
:1. Introduction
1.1. Statistics for Differential Test Functioning
1.2. Statistics for Differential Response Functioning
2. Materials and Methods
2.1. Data Analysis and Evaluation Measures
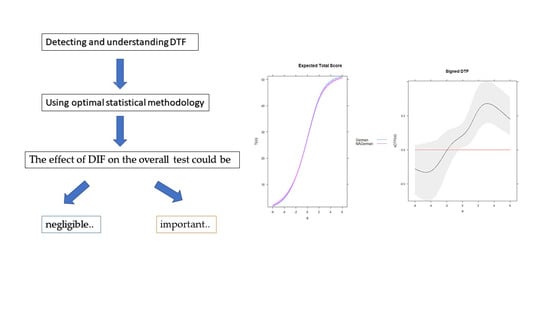
2.2. Real Data Illustration
3. Results
3.1. When No Items Contained DIF
3.2. The Results of DTF Statistics When the Items Contained Uniform DIF
3.3. The Results of DTF Statistics When the Items Contained Non-Uniform DIF
3.4. The Results of Mean Effect Size Values and the Empirical Standard Errors for DTF Statistics When the Items Contained Uniform/Non-Uniform DIF
3.5. The Results of the Real Data Illustrations
4. Discussion
5. Conclusions
Supplementary Materials
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chalmers, R.P.; Counsell, A.; Flora, D.B. It might not make a big DIF: Improved Differential Test Functioning statistics that account for sampling variability. Educ. Psychol. Meas. 2016, 76, 114–140. [Google Scholar] [CrossRef] [Green Version]
- Drasgow, F. Study of the measurement bias of two standardized psychological tests. J. Appl. Psychol. 1987, 72, 19–29. [Google Scholar] [CrossRef]
- DeMars, C.E. An analytic comparison of effect sizes for differential item functioning. Appl. Meas. Educ. 2011, 24, 189–209. [Google Scholar] [CrossRef]
- Stark, S.; Chernyshenko, O.S.; Drasgow, F. Examining the effects of differential item functioning and differential test functioning on selection decisions: When are statistically significant effects practically important? J. Appl. Psychol. 2004, 89, 497–508. [Google Scholar] [CrossRef]
- Pae, T.; Park, G. Examining the relationship between differential item functioning and differential test functioning. Lang. Test. 2006, 23, 475–496. [Google Scholar] [CrossRef]
- Flora, D.; Curran, P.; Hussong, A.; Edwards, M. Incorporating measurement nonequivalence in a cross-study latent growth curve analysis. Struct. Equ. Model. A Multidiscip. J. 2008, 15, 676–704. [Google Scholar] [CrossRef]
- Hunter, C. A Simulation Study Comparing Two Methods ff Evaluating Differential Test Functioning (DTF): DFIT and the Mantel-Haenszel/Liu-Agresti Variance. Ph.D. Thesis, Georgia State University, Atlanta, GA, USA, 2014. Available online: https://core.ac.uk/download/pdf/71425819.pdf (accessed on 3 April 2023).
- Raju, N.S.; van der Linden, W.J.; Fleer, P.F. IRT-based internal measures of differential functioning of items and tests. Appl. Psychol. Meas. 1995, 19, 353–368. [Google Scholar] [CrossRef] [Green Version]
- Chalmers, R.P. Model-Based Measures for Detecting and Quantifying Response Bias. Psychometrika 2018, 83, 696–732. [Google Scholar] [CrossRef]
- Chang, H.-H.; Mazzeo, J.; Roussos, L. DIF for polytomously scored items: An adaptation of the SIBTEST procedure. J. Educ. Meas. 1996, 33, 333–353. [Google Scholar] [CrossRef]
- Shealy, R.; Stout, W. A model-based standardization approach that separates true bias/DIF from group ability differences and detects test bias/DTF as well as item bias/DIF. Psychometrika 1993, 58, 159–194. [Google Scholar] [CrossRef]
- Li, H.-H.; Stout, W. A new procedure for detection of crossing DIF. Psychometrika 1996, 61, 647–677. [Google Scholar] [CrossRef]
- Oshima, T.C.; Raju, N.S.; Flowers, C.P.; Slinde, J.A. Differential bundle functioning using the DFIT framework: Procedures for identifying possible sources of differential functioning. Appl. Meas. Educ. 1998, 11, 353–369. [Google Scholar] [CrossRef]
- Chalmers, R.P. A differential response functioning framework for understanding item, bundle, and test bias. Unpublished. Ph.D. Thesis, York University, Toronto, ON, Canada, October 2016. Available online: https://yorkspace.library.yorku.ca/xmlui/handle/10315/33431 (accessed on 3 April 2023).
- Finch, W.H.; French, B.F. Effect Sizes for Estimating Differential Item Functioning Influence at the Test Level. Psych 2023, 5, 133–147. [Google Scholar] [CrossRef]
- Camilli, G.; Penfield, R.A. Variance estimation for Differential Test Functioning based on Mantel-Haenszel statistics. J. Educ. Meas. 1997, 34, 123–139. [Google Scholar] [CrossRef]
- Finch, W.H.; French, B.F.; Hernandez, M.F. Quantifying Item Invariance for the Selection of the Least Biased Assessment. J. Appl. Meas. 2019, 20, 13–26. [Google Scholar]
- Hasselblad, V.; Hedges, L.V. Meta-analysis of screening and diagnostic tests. Psychol. Bull. 1995, 117, 167–178. [Google Scholar] [CrossRef]
- Zumbo, B.D.; Thomas, D.R. A Measure of Effect Size for a Model-Based Approach for Studying DIF (Working Paper of the Edgeworth Laboratory for Quantitative Behavioral Science); Canada University of Northern British Columbia: Prince George, BC, Canada, 1997. [Google Scholar]
- Doebler, A. Looking at DIF from a new perspective: A structure-based approach acknowledging inherent indefinability. Appl. Psychol. Meas. 2019, 43, 303–321. [Google Scholar] [CrossRef] [PubMed]
- Wainer, H. Model-based standardized measurement of an item’s differential impact. In Differential Item functioning; Holland, P.W., Wainer, H., Eds.; Lawrence Erlbaum Associates, Inc.: Hillsdale, NJ, USA, 1993; pp. 123–135. [Google Scholar]
- Oshima, T.C.; Raju, N.S.; Flowers, C.P. Development and demonstration of multidimensional IRT-based internal measures of differential functioning of items and tests. J. Educ. Meas. 1997, 34, 253–272. [Google Scholar] [CrossRef]
- Guttman, L. A basis for analyzing test-retest reliability. Psychometrika 1945, 10, 255–282. [Google Scholar] [CrossRef]
- Lord, F.M.; Novick, M.R. Statistical Theory of Mental Test Scores; Addison-Wesley: Reading, MA, USA, 1968. [Google Scholar]
- Robitzsch, A. Robust and Nonrobust Linking of Two Groups for the Rasch Model with Balanced and Unbalanced Random DIF: A Comparative Simulation Study and the Simultaneous Assessment of Standard Errors and Linking Errors with Resampling Techniques. Symmetry 2021, 13, 2198. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2022; Available online: https://www.R-project.org/ (accessed on 3 April 2023).
- Chalmers, R.P. Mirt: A multidimensional item response theory package for the R environment. J. Stat. Softw. 2012, 48, 1–29. [Google Scholar] [CrossRef] [Green Version]
- Corporation, M.; Weston, S. DoParallel: Foreach Parallel Adaptor for the ‘Parallel’ Package, R package version 1.0.14; 2018. Available online: https://CRAN.R-project.org/package=doParallel (accessed on 3 April 2023).
- Bradley, J.V. Robustness? Br. J. Math. Stat. Psychol. 1978, 31, 144–152. [Google Scholar] [CrossRef]
- Schult, J.; Wagner, S. VERA 8 in Baden-Württemberg 2019. In Beiträge zur Bildungsberichterstattung; Institut für Bildungsanalysen Baden-Württemberg: Stuttgart, Germany, 2019; Available online: https://ibbw.kultus-bw.de/site/pbs-bw-km-root/get/documents_E56497547/KULTUS.Dachmandant/KULTUS/Dienststellen/ibbw/Systemanalysen/Bildungsberichterstattung/Ergebnisberichte/VERA_8/Ergebnisse_VERA8_2019.pdf (accessed on 3 April 2023).
- Lee, S. Lord’s Wald test for detecting DIF in multidimensional IRT models. Unpublished. Ph.D. Thesis, The State University of New Jersey, New Jersey, NJ, USA, 2015. Available online: https://doi.org/doi:10.7282/T3JH3P13 (accessed on 3 April 2023).
- Wang, C.; Zhu, R.; Xu, G. Using Lasso and Adaptive Lasso to Identify DIF in Multidimensional 2PL Models. Multivar. Behav. Res. 2023, 58, 387–407. [Google Scholar] [CrossRef] [PubMed]
- Zumbo, B.D. Three Generations of DIF Analyses: Considering Where It Has Been, Where It Is Now, and Where It Is Going. Lang. Assess. Q. 2007, 4, 223–233. [Google Scholar] [CrossRef]
- Camilli, G. Test Fairness. In Educational Measurement, 4th ed.; Brennan, R., Ed.; American Council on Education and Praeger: Westport, CT, USA, 2006; pp. 221–256. [Google Scholar]
- Penfield, R.D.; Camilli, G. Differential item functioning and item bias. In Handbook of Statistics; Rao, C.R., Sinharay, S., Eds.; Routledge: Oxford, UK, 2007; Volume 26, pp. 125–167. [Google Scholar]
- Martinková, P.; Drabinová, A.; Liaw, Y.L.; Sanders, E.A.; McFarland, J.L.; Price, R.M. Checking Equity: Why Differential Item Functioning Analysis Should Be a Routine Part of Developing Conceptual Assessments. CBE Life Sci. Educ. 2017, 16, rm2. [Google Scholar] [CrossRef] [PubMed] [Green Version]

| Ability | N 1 | sDTF | sDRF | uDRF | SIBT | CSIBT | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| p < 0.10 | p < 0.05 | p < 0.01 | p < 0.10 | p < 0.05 | p < 0.01 | p < 0.10 | p < 0.05 | p < 0.01 | p < 0.10 | p < 0.05 | p < 0.01 | p < 0.10 | p < 0.05 | p < 0.01 | ||
| µθR = µθF = 0 | 250/250 | 0.10 | 0.05 | 0.01 | 0.08 | 0.04 | 0.01 | 0.32 | 0.19 | 0.07 | 0.12 | 0.06 | 0.01 | 0.16 | 0.08 | 0.02 |
| 500/500 | 0.09 | 0.04 | 0.01 | 0.09 | 0.05 | 0.00 | 0.26 | 0.16 | 0.06 | 0.1 | 0.05 | 0.01 | 0.13 | 0.07 | 0.01 | |
| 1000/250 | 0.11 | 0.06 | 0.01 | 0.1 | 0.04 | 0.00 | 0.27 | 0.19 | 0.05 | 0.1 | 0.06 | 0.02 | 0.15 | 0.09 | 0.02 | |
| 1000/500 | 0.10 | 0.05 | 0.00 | 0.06 | 0.02 | 0.00 | 0.24 | 0.16 | 0.04 | 0.1 | 0.05 | 0.02 | 0.12 | 0.06 | 0.02 | |
| 1000/1000 | 0.08 | 0.04 | 0.01 | 0.16 | 0.08 | 0.02 | 0.28 | 0.18 | 0.09 | 0.11 | 0.05 | 0.01 | 0.14 | 0.08 | 0.02 | |
| 2000/250 | 0.11 | 0.06 | 0.01 | 0.13 | 0.06 | 0.01 | 0.32 | 0.23 | 0.07 | 0.10 | 0.05 | 0.01 | 0.15 | 0.08 | 0.02 | |
| 2000/500 | 0.08 | 0.04 | 0.01 | 0.14 | 0.08 | 0.02 | 0.27 | 0.17 | 0.1 | 0.12 | 0.07 | 0.01 | 0.16 | 0.09 | 0.02 | |
| 2000/2000 | 0.09 | 0.05 | 0.01 | 0.13 | 0.06 | 0.01 | 0.3 | 0.23 | 0.13 | 0.10 | 0.05 | 0.00 | 0.14 | 0.07 | 0.01 | |
| 5000/5000 | 0.11 | 0.05 | 0.01 | 0.14 | 0.06 | 0.01 | 0.27 | 0.17 | 0.06 | 0.09 | 0.04 | 0.01 | 0.12 | 0.07 | 0.01 | |
| µθR = 0.0/µθF = −1.0 | 250/250 | 0.12 | 0.06 | 0.01 | 0.11 | 0.04 | 0.00 | 0.21 | 0.15 | 0.07 | 0.12 | 0.07 | 0.02 | 0.17 | 0.10 | 0.03 |
| 500/500 | 0.11 | 0.06 | 0.02 | 0.12 | 0.08 | 0.02 | 0.3 | 0.19 | 0.04 | 0.14 | 0.08 | 0.02 | 0.19 | 0.11 | 0.03 | |
| 1000/250 | 0.12 | 0.08 | 0.03 | 0.07 | 0.04 | 0.00 | 0.21 | 0.11 | 0.02 | 0.14 | 0.07 | 0.02 | 0.20 | 0.12 | 0.04 | |
| 1000/500 | 0.12 | 0.07 | 0.02 | 0.2 | 0.14 | 0.04 | 0.33 | 0.22 | 0.11 | 0.14 | 0.08 | 0.01 | 0.20 | 0.11 | 0.03 | |
| 1000/1000 | 0.09 | 0.05 | 0.01 | 0.09 | 0.04 | 0.01 | 0.28 | 0.18 | 0.09 | 0.14 | 0.08 | 0.02 | 0.21 | 0.12 | 0.03 | |
| 2000/250 | 0.13 | 0.08 | 0.03 | 0.17 | 0.06 | 0.01 | 0.22 | 0.15 | 0.03 | 0.14 | 0.07 | 0.03 | 0.20 | 0.12 | 0.05 | |
| 2000/500 | 0.12 | 0.06 | 0.02 | 0.11 | 0.07 | 0.01 | 0.26 | 0.10 | 0.02 | 0.14 | 0.08 | 0.02 | 0.19 | 0.12 | 0.04 | |
| 2000/2000 | 0.10 | 0.05 | 0.01 | 0.07 | 0.01 | 0.00 | 0.18 | 0.12 | 0.03 | 0.14 | 0.09 | 0.02 | 0.24 | 0.15 | 0.05 | |
| 5000/5000 | 0.10 | 0.05 | 0.01 | 0.10 | 0.03 | 0.00 | 0.25 | 0.15 | 0.05 | 0.15 | 0.09 | 0.02 | 0.33 | 0.22 | 0.09 | |
| Ability | N | sDTF | %sDTF | uDTF | %uDTF | sDRF | uDRF | dDRF | SIBT | CSIBT | seSIBT |
|---|---|---|---|---|---|---|---|---|---|---|---|
| µθR = µθF = 0 | 250/250 | 0.003 | 0.014 | 0.09 | 0.448 | −0.015 | 0.105 | 0.117 | 0.003 | 0.108 | 0.092 |
| 500/500 | 0.002 | 0.01 | 0.062 | 0.310 | −0.005 | 0.07 | 0.079 | 0 | 0.07 | 0.064 | |
| 1000/250 | 0.004 | 0.019 | 0.071 | 0.354 | 0.011 | 0.079 | 0.088 | 0.003 | 0.082 | 0.073 | |
| 1000/500 | 0.001 | 0.005 | 0.054 | 0.271 | 0.002 | 0.061 | 0.068 | −0.003 | 0.06 | 0.055 | |
| 1000/1000 | −0.001 | −0.006 | 0.043 | 0.215 | 0.001 | 0.052 | 0.059 | 0 | 0.051 | 0.045 | |
| 2000/250 | 0.006 | 0.028 | 0.065 | 0.326 | 0 | 0.078 | 0.088 | 0.001 | 0.078 | 0.069 | |
| 2000/500 | 0.002 | 0.01 | 0.048 | 0.238 | 0.004 | 0.059 | 0.065 | −0.002 | 0.059 | 0.05 | |
| 2000/2000 | 0.001 | 0.003 | 0.03 | 0.152 | −0.005 | 0.038 | 0.042 | −0.001 | 0.036 | 0.031 | |
| 5000/5000 | 0 | −0.001 | 0.019 | 0.097 | −0.001 | 0.022 | 0.025 | −0.001 | 0.022 | 0.02 | |
| µθR = 0.0/µθF = −1.0 | 250/250 | 0.013 | 0.064 | 0.113 | 0.564 | 0.006 | 0.103 | 0.116 | 0.014 | 0.12 | 0.102 |
| 500/500 | 0.009 | 0.043 | 0.081 | 0.407 | 0.002 | 0.079 | 0.09 | 0.002 | 0.084 | 0.07 | |
| 1000/250 | 0.02 | 0.101 | 0.101 | 0.505 | −0.006 | 0.092 | 0.105 | −0.004 | 0.101 | 0.086 | |
| 1000/500 | 0.015 | 0.076 | 0.077 | 0.386 | 0.003 | 0.078 | 0.089 | −0.004 | 0.077 | 0.063 | |
| 1000/1000 | 0.004 | 0.019 | 0.054 | 0.271 | −0.015 | 0.053 | 0.061 | −0.003 | 0.062 | 0.049 | |
| 2000/250 | 0.023 | 0.116 | 0.098 | 0.49 | −0.001 | 0.106 | 0.12 | −0.007 | 0.101 | 0.085 | |
| 2000/500 | 0.009 | 0.046 | 0.07 | 0.349 | 0.015 | 0.071 | 0.082 | −0.006 | 0.076 | 0.062 | |
| 2000/2000 | 0.001 | 0.007 | 0.04 | 0.2 | 0.005 | 0.035 | 0.04 | −0.002 | 0.047 | 0.034 | |
| 5000/5000 | 0.00 | 0.00 | 0.025 | 0.125 | −0.003 | 0.023 | 0.026 | −0.005 | 0.035 | 0.022 |
| Ability | N | sDTF | %sDTF | uDTF | %uDTF | sDRF | uDRF | dDRF | SIBT | CSIBT | seSIBT |
|---|---|---|---|---|---|---|---|---|---|---|---|
| µθR = µθF = 0 | 250/250 | 0.071 | 0.355 | 0.05 | 0.252 | 0.086 | 0.051 | 0.056 | 0.094 | 0.064 | 0.004 |
| 500/500 | 0.049 | 0.244 | 0.035 | 0.175 | 0.057 | 0.034 | 0.038 | 0.063 | 0.043 | 0.001 | |
| 1000/250 | 0.056 | 0.279 | 0.040 | 0.202 | 0.071 | 0.04 | 0.044 | 0.075 | 0.049 | 0.003 | |
| 1000/500 | 0.043 | 0.215 | 0.029 | 0.143 | 0.045 | 0.03 | 0.033 | 0.056 | 0.036 | 0.001 | |
| 1000/1000 | 0.034 | 0.169 | 0.023 | 0.117 | 0.048 | 0.03 | 0.033 | 0.044 | 0.031 | 0.001 | |
| 2000/250 | 0.052 | 0.260 | 0.038 | 0.192 | 0.074 | 0.047 | 0.052 | 0.069 | 0.047 | 0.003 | |
| 2000/500 | 0.038 | 0.188 | 0.027 | 0.135 | 0.056 | 0.032 | 0.035 | 0.053 | 0.035 | 0.001 | |
| 2000/2000 | 0.024 | 0.118 | 0.016 | 0.079 | 0.03 | 0.022 | 0.024 | 0.031 | 0.022 | 0.000 | |
| 5000/5000 | 0.016 | 0.078 | 0.010 | 0.054 | 0.022 | 0.014 | 0.015 | 0.019 | 0.013 | 0.000 | |
| µθR = 0.0/µθF = −1.0 | 250/250 | 0.103 | 0.515 | 0.065 | 0.326 | 0.092 | 0.057 | 0.062 | 0.108 | 0.071 | 0.006 |
| 500/500 | 0.076 | 0.380 | 0.048 | 0.242 | 0.071 | 0.038 | 0.043 | 0.077 | 0.053 | 0.003 | |
| 1000/250 | 0.097 | 0.485 | 0.064 | 0.322 | 0.082 | 0.042 | 0.049 | 0.093 | 0.061 | 0.006 | |
| 1000/500 | 0.075 | 0.375 | 0.049 | 0.244 | 0.078 | 0.044 | 0.05 | 0.07 | 0.046 | 0.003 | |
| 1000/1000 | 0.051 | 0.257 | 0.033 | 0.165 | 0.047 | 0.03 | 0.034 | 0.054 | 0.037 | 0.001 | |
| 2000/250 | 0.094 | 0.472 | 0.063 | 0.313 | 0.104 | 0.051 | 0.059 | 0.094 | 0.061 | 0.007 | |
| 2000/500 | 0.068 | 0.338 | 0.043 | 0.216 | 0.065 | 0.039 | 0.046 | 0.068 | 0.047 | 0.004 | |
| 2000/2000 | 0.038 | 0.188 | 0.024 | 0.120 | 0.028 | 0.018 | 0.02 | 0.038 | 0.029 | 0.001 | |
| 5000/5000 | 0.023 | 0.113 | 0.014 | 0.069 | 0.011 | 0.011 | 0.012 | 0.024 | 0.02 | 0.000 |
| 10% DIF (Two Items Contained DIF) | 20% DIF (Four Items Contained DIF) | ||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| sDTF | sDRF | uDRF | SIBT | CSIB | sDTF | sDRF | uDRF | SIBT | CSIB | ||||||||||||
| N | L 2 | M | L | M | L | M | L | M | L | M | L | M | L | M | L | M | L | M | L | M | |
| UB 1 | 250/250 | 0.30 | 0.84 | 0.38 | 0.88 | 0.44 | 0.86 | 0.32 | 0.86 | 0.34 | 0.86 | 0.50 | 0.99 | 0.60 | 1.0 | 0.63 | 0.99 | 0.58 | 0.99 | 0.58 | 0.99 |
| 500/500 | 0.59 | 0.98 | 0.53 | 0.99 | 0.54 | 0.99 | 0.62 | 0.99 | 0.62 | 0.99 | 0.85 | 1.0 | 0.89 | 1.0 | 0.85 | 1.0 | 0.88 | 1.0 | 0.86 | 1.0 | |
| 1000/250 | 0.47 | 0.98 | 0.49 | 0.98 | 0.50 | 0.97 | 0.50 | 0.98 | 0.50 | 0.98 | 0.73 | 1.0 | 0.79 | 1.0 | 0.81 | 1.0 | 0.80 | 1.0 | 0.80 | 1.0 | |
| 1000/500 | 0.73 | 1.0 | 0.71 | 1.0 | 0.74 | 0.99 | 0.71 | 1.0 | 0.71 | 1.0 | 0.93 | 1.0 | 0.93 | 1.0 | 0.92 | 1.0 | 0.95 | 1.0 | 0.95 | 1.0 | |
| 1000/1000 | 0.90 | 1.0 | 0.90 | 1.0 | 0.92 | 1.0 | 0.90 | 1.0 | 0.89 | 1.0 | 0.99 | 1.0 | 0.99 | 1.0 | 0.99 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | |
| 2000/250 | 0.53 | 0.98 | 0.60 | 0.99 | 0.60 | 0.99 | 0.54 | 0.98 | 0.55 | 0.98 | 0.79 | 1.0 | 0.83 | 1.0 | 0.86 | 1.0 | 0.82 | 1.0 | 0.82 | 1.0 | |
| 2000/500 | 0.79 | 1.0 | 0.82 | 1.0 | 0.80 | 1.0 | 0.82 | 1.0 | 0.82 | 1.0 | 0.96 | 1.0 | 0.99 | 1.0 | 0.99 | 1.0 | 0.97 | 1.0 | 0.97 | 1.0 | |
| 2000/2000 | 1.0 | 1.0 | 1.0 | 1.0 | 0.99 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | |
| 5000/5000 | 1 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | |
| B 1 | 250/250 | 0.04 | 0.03 | 0.05 | 0.03 | 0.18 | 0.22 | 0.05 | 0.05 | 0.07 | 0.07 | 0.04 | 0.06 | 0.09 | 0.09 | 0.15 | 0.22 | 0.05 | 0.07 | 0.08 | 0.09 |
| 500/500 | 0.05 | 0.05 | 0.07 | 0.05 | 0.18 | 0.20 | 0.05 | 0.07 | 0.07 | 0.09 | 0.07 | 0.11 | 0.05 | 0.10 | 0.20 | 0.16 | 0.06 | 0.07 | 0.08 | 0.08 | |
| 1000/250 | 0.04 | 0.04 | 0.02 | 0.05 | 0.17 | 0.19 | 0.05 | 0.05 | 0.06 | 0.07 | 0.05 | 0.08 | 0.02 | 0.09 | 0.13 | 0.23 | 0.06 | 0.05 | 0.08 | 0.07 | |
| 1000/500 | 0.05 | 0.06 | 0.07 | 0.07 | 0.16 | 0.26 | 0.05 | 0.05 | 0.07 | 0.08 | 0.06 | 0.12 | 0.04 | 0.06 | 0.18 | 0.25 | 0.06 | 0.06 | 0.08 | 0.09 | |
| 1000/1000 | 0.06 | 0.07 | 0.03 | 0.02 | 0.13 | 0.21 | 0.05 | 0.06 | 0.07 | 0.09 | 0.08 | 0.16 | 0.02 | 0.07 | 0.19 | 0.23 | 0.06 | 0.08 | 0.09 | 0.09 | |
| 2000/250 | 0.04 | 0.05 | 0.06 | 0.05 | 0.18 | 0.20 | 0.05 | 0.05 | 0.07 | 0.07 | 0.06 | 0.09 | 0.06 | 0.07 | 0.19 | 0.24 | 0.06 | 0.06 | 0.09 | 0.09 | |
| 2000/500 | 0.05 | 0.07 | 0.08 | 0.11 | 0.22 | 0.27 | 0.05 | 0.07 | 0.08 | 0.10 | 0.07 | 0.14 | 0.06 | 0.07 | 0.16 | 0.29 | 0.07 | 0.07 | 0.09 | 0.09 | |
| 2000/2000 | 0.07 | 0.13 | 0.04 | 0.05 | 0.19 | 0.25 | 0.04 | 0.07 | 0.07 | 0.10 | 0.11 | 0.31 | 0.02 | 0.13 | 0.18 | 0.31 | 0.06 | 0.09 | 0.07 | 0.11 | |
| 5000/5000 | 0.09 | 0.23 | 0.06 | 0.05 | 0.18 | 0.32 | 0.07 | 0.10 | 0.09 | 0.13 | 0.21 | 0.67 | 0.04 | 0.11 | 0.15 | 0.52 | 0.06 | 0.12 | 0.09 | 0.14 | |
| DIF | N | 10% DIF (Two Items Contained DIF) | 20% DIF (Four Items Contained DIF) | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| sDTF | sDRF | uDRF | SIBT | CSIB | sDTF | sDRF | uDRF | SIBT | CSIB | ||||||||||||
| L 2 | M | L | M | L | M | L | M | L | M | L | M | L | M | L | M | L | M | L | M | ||
| UB 1 | 250/250 | 0.04 | 0.04 | 0.07 | 0.01 | 0.34 | 0.52 | 0.06 | 0.06 | 0.10 | 0.20 | 0.03 | 0.04 | 0.06 | 0.05 | 0.41 | 0.8 | 0.05 | 0.06 | 0.14 | 0.39 |
| 500/500 | 0.05 | 0.05 | 0.07 | 0.04 | 0.51 | 0.86 | 0.04 | 0.05 | 0.15 | 0.38 | 0.05 | 0.06 | 0.05 | 0.03 | 0.65 | 1.0 | 0.05 | 0.06 | 0.27 | 0.70 | |
| 1000/250 | 0.05 | 0.04 | 0.05 | 0.05 | 0.45 | 0.80 | 0.05 | 0.06 | 0.10 | 0.28 | 0.06 | 0.06 | 0.03 | 0.06 | 0.65 | 0.96 | 0.06 | 0.06 | 0.22 | 0.58 | |
| 1000/500 | 0.05 | 0.06 | 0.06 | 0.05 | 0.57 | 0.93 | 0.06 | 0.06 | 0.16 | 0.48 | 0.05 | 0.08 | 0.05 | 0.07 | 0.73 | 1.0 | 0.05 | 0.06 | 0.32 | 0.83 | |
| 1000/1000 | 0.06 | 0.06 | 0.05 | 0.06 | 0.64 | 0.98 | 0.05 | 0.06 | 0.26 | 0.72 | 0.05 | 0.07 | 0.09 | 0.09 | 0.9 | 1.0 | 0.06 | 0.07 | 0.50 | 0.97 | |
| 2000/250 | 0.04 | 0.05 | 0.04 | 0.09 | 0.44 | 0.91 | 0.04 | 0.05 | 0.11 | 0.30 | 0.05 | 0.04 | 0.07 | 0.05 | 0.66 | 0.96 | 0.05 | 0.06 | 0.22 | 0.62 | |
| 2000/500 | 0.03 | 0.06 | 0.06 | 0.02 | 0.62 | 0.96 | 0.04 | 0.06 | 0.21 | 0.54 | 0.06 | 0.08 | 0.12 | 0.02 | 0.94 | 1.0 | 0.06 | 0.06 | 0.40 | 0.90 | |
| 2000/2000 | 0.06 | 0.09 | 0.06 | 0.06 | 0.91 | 1.0 | 0.06 | 0.07 | 0.47 | 0.96 | 0.06 | 0.09 | 0.05 | 0.09 | 1.0 | 1.0 | 0.05 | 0.07 | 0.80 | 1.0 | |
| 5000/5000 | 0.09 | 0.14 | 0.03 | 0.03 | 0.99 | 1.0 | 0.06 | 0.07 | 0.86 | 1.0 | 0.09 | 0.20 | 0.06 | 0.08 | 1.0 | 1.0 | 0.07 | 0.10 | 1.0 | 1.0 | |
| B 1 | 250/250 | 0.05 | 0.06 | 0.04 | 0.02 | 0.18 | 0.16 | 0.05 | 0.05 | 0.07 | 0.07 | 0.04 | 0.06 | 0.07 | 0.09 | 0.16 | 0.16 | 0.06 | 0.04 | 0.08 | 0.06 |
| 500/500 | 0.04 | 0.07 | 0.02 | 0.05 | 0.15 | 0.21 | 0.06 | 0.06 | 0.08 | 0.08 | 0.05 | 0.10 | 0.04 | 0.02 | 0.18 | 0.20 | 0.05 | 0.07 | 0.07 | 0.08 | |
| 1000/250 | 0.06 | 0.05 | 0.06 | 0.06 | 0.13 | 0.18 | 0.05 | 0.06 | 0.07 | 0.08 | 0.03 | 0.07 | 0.05 | 0.05 | 0.21 | 0.21 | 0.06 | 0.06 | 0.10 | 0.09 | |
| 1000/500 | 0.06 | 0.07 | 0.05 | 0.03 | 0.16 | 0.24 | 0.06 | 0.07 | 0.07 | 0.10 | 0.05 | 0.12 | 0.07 | 0.02 | 0.20 | 0.25 | 0.05 | 0.06 | 0.08 | 0.09 | |
| 1000/1000 | 0.04 | 0.07 | 0.02 | 0.05 | 0.14 | 0.19 | 0.04 | 0.06 | 0.07 | 0.09 | 0.07 | 0.14 | 0.11 | 0.04 | 0.25 | 0.21 | 0.07 | 0.07 | 0.09 | 0.08 | |
| 2000/250 | 0.04 | 0.06 | 0.07 | 0.05 | 0.18 | 0.20 | 0.07 | 0.05 | 0.10 | 0.07 | 0.04 | 0.06 | 0.05 | 0.03 | 0.33 | 0.19 | 0.05 | 0.07 | 0.08 | 0.09 | |
| 2000/500 | 0.06 | 0.07 | 0.02 | 0.04 | 0.19 | 0.17 | 0.06 | 0.06 | 0.08 | 0.09 | 0.05 | 0.10 | 0.03 | 0.06 | 0.21 | 0.17 | 0.07 | 0.08 | 0.10 | 0.10 | |
| 2000/2000 | 0.07 | 0.13 | 0.04 | 0.08 | 0.21 | 0.29 | 0.07 | 0.06 | 0.09 | 0.09 | 0.13 | 0.24 | 0.06 | 0.08 | 0.21 | 0.38 | 0.05 | 0.10 | 0.08 | 0.12 | |
| 5000/5000 | 0.13 | 0.22 | 0.02 | 0.12 | 0.21 | 0.47 | 0.06 | 0.08 | 0.09 | 0.12 | 0.23 | 0.60 | 0.08 | 0.13 | 0.24 | 0.78 | 0.10 | 0.16 | 0.10 | 0.18 | |
| Stat. | Dif Mag. | Mean Effect Size Values | Empirical Standard Errors | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Uniform DIF | Non-Uniform DIF | Uniform DIF | Non-Uniform DIF | ||||||||||||||
| 10% DIF | 20% DIF | 10% DIF | 20% DIF | 10% DIF | 20% DIF | 10% DIF | 20% DIF | ||||||||||
| UB 1 | B | UB | B | UB | B | UB | B | UB | B | UB | B | UB | B | UB | B | ||
| sDTF | 0.25 | −0.032 | −0.003 | −0.072 | −0.009 | −0.002 | 0.003 | −0.004 | 0.009 | 0.005 | 0.005 | 0.007 | 0.007 | 0.004 | 0.004 | 0.007 | 0.009 |
| 0.50 | −0.064 | −0.006 | −0.145 | −0.018 | −0.003 | 0.005 | −0.007 | 0.015 | 0.005 | 0.005 | 0.008 | 0.008 | 0.004 | 0.004 | 0.007 | 0.007 | |
| %sDTF | 0.25 | −0.158 | −0.015 | −0.361 | −0.045 | −0.01 | 0.027 | −0.021 | 0.045 | 0.023 | 0.023 | 0.037 | 0.036 | 0.022 | 0.022 | 0.035 | 0.035 |
| 0.50 | −0.318 | −0.028 | −0.726 | −0.09 | −0.017 | 0.024 | −0.036 | 0.077 | 0.024 | 0.024 | 0.04 | 0.039 | 0.021 | 0.02 | 0.035 | 0.035 | |
| uDTF | 0.25 | 0.032 | 0.008 | 0.072 | 0.016 | 0.029 | 0.009 | 0.073 | 0.014 | 0.005 | 0.004 | 0.007 | 0.006 | 0.006 | 0.004 | 0.012 | 0.006 |
| 0.50 | 0.064 | 0.009 | 0.145 | 0.022 | 0.05 | 0.011 | 0.125 | 0.019 | 0.005 | 0.004 | 0.008 | 0.006 | 0.006 | 0.004 | 0.011 | 0.005 | |
| %uDTF | 0.25 | 0.159 | 0.04 | 0.362 | 0.078 | 0.144 | 0.044 | 0.366 | 0.071 | 0.023 | 0.02 | 0.037 | 0.032 | 0.032 | 0.02 | 0.059 | 0.028 |
| 0.50 | 0.318 | 0.047 | 0.726 | 0.108 | 0.248 | 0.054 | 0.624 | 0.093 | 0.024 | 0.019 | 0.04 | 0.028 | 0.031 | 0.021 | 0.054 | 0.025 | |
| sDRF | 0.25 | 0.093 | −0.004 | 0.196 | 0.008 | 0.001 | −0.004 | 0.004 | −0.009 | 0.013 | 0.013 | 0.02 | 0.018 | 0.012 | 0.012 | 0.02 | 0.012 |
| 0.50 | 0.184 | −0.007 | 0.39 | 0.013 | 0.005 | −0.006 | 0.006 | −0.017 | 0.013 | 0.011 | 0.019 | 0.021 | 0.012 | 0.015 | 0.017 | 0.011 | |
| uDRF | 0.25 | 0.093 | 0.016 | 0.196 | 0.023 | 0.053 | 0.016 | 0.118 | 0.024 | 0.013 | 0.007 | 0.02 | 0.01 | 0.012 | 0.007 | 0.02 | 0.012 |
| 0.50 | 0.184 | 0.018 | 0.39 | 0.029 | 0.099 | 0.019 | 0.212 | 0.03 | 0.013 | 0.008 | 0.019 | 0.013 | 0.013 | 0.007 | 0.017 | 0.011 | |
| dDRF | 0.25 | 0.099 | 0.017 | 0.203 | 0.027 | 0.058 | 0.018 | 0.13 | 0.028 | 0.013 | 0.008 | 0.021 | 0.011 | 0.013 | 0.008 | 0.022 | 0.013 |
| 0.50 | 0.193 | 0.02 | 0.404 | 0.035 | 0.108 | 0.022 | 0.233 | 0.035 | 0.014 | 0.009 | 0.02 | 0.013 | 0.014 | 0.007 | 0.019 | 0.011 | |
| SIB | 0.25 | −0.095 | 0.003 | −0.081 | 0.108 | −0.003 | 0.004 | −0.007 | 0.01 | 0.013 | 0.014 | 0.013 | 0.013 | 0.013 | 0.013 | 0.021 | 0.021 |
| 0.50 | −0.189 | 0.008 | −0.16 | −0.017 | −0.005 | 0.006 | −0.012 | 0.018 | 0.014 | 0.013 | 0.013 | 0.019 | 0.013 | 0.013 | 0.02 | 0.020 | |
| CSIB | 0.25 | 0.095 | 0.015 | 0.081 | 0.108 | 0.046 | 0.015 | 0.098 | 0.024 | 0.013 | 0.009 | 0.013 | 0.013 | 0.013 | 0.009 | 0.02 | 0.014 |
| 0.50 | 0.189 | 0.017 | 0.16 | 0.024 | 0.084 | 0.017 | 0.181 | 0.026 | 0.014 | 0.01 | 0.013 | 0.024 | 0.013 | 0.009 | 0.021 | 0.015 | |
| DTF Measures | Intercept (d) | Slope (a) | Intercept (d) and Slope (a) | |
|---|---|---|---|---|
| sDTF | sDTF | 0.074 | −0.069 | 0.075 |
| p | 0.174 | 0.213 | 0.303 | |
| CI_97.5 | 0.183 | 0.042 | 0.225 | |
| CI_2.5% | −0.030 | −0.171 | −0.062 | |
| uDTF | uDTF | 0.077 | 0.203 | 0.468 |
| CI_97.5 | 0.183 | 0.394 | 0.703 | |
| CI_2.5% | 0.038 | 0.078 | 0.268 | |
| %sDTF | %sDTF | 0.142 | −0.132 | 0.143 |
| CI_97.5 | 0.352 | 0.081 | 0.434 | |
| CI_2.5% | −0.058 | −0.329 | −0.119 | |
| %uDTF | %uDTF | 0.077 | 0.390 | 0.901 |
| CI_97.5 | 0.183 | 0.759 | 1.351 | |
| CI_2.5% | 0.038 | 0.149 | 0.514 | |
| sDRF | sDRF | −0.132 | 0.016 | −0.208 |
| p | 0.160 | 0.591 | 0.009 | |
| CI_97.5 | 0.048 | 0.071 | −0.050 | |
| CI_2.5% | −0.320 | −0.043 | −0.359 | |
| uDRF | uDRF | 0.135 | 0.050 | 0.255 |
| p | 0.035 | 0.218 | 0.000 | |
| CI_97.5 | 0.315 | 0.157 | 0.397 | |
| CI_2.5% | 0.042 | 0.014 | 0.131 | |
| dDRF | dDRF | 0.151 | 0.070 | 0.289 |
| CI_97.5 | 0.334 | 0.198 | 0.450 | |
| CI_2.5% | 0.051 | 0.026 | 0.154 | |
| SIBTEST | beta | 0.113 | 0.129 | 0.237 |
| X2 | 1.885 | 4.106 | 8.504 | |
| p | 0.170 | 0.043 | 0.004 | |
| CSIBTEST | beta | 0.107 | 0.129 | 0.237 |
| X2 | 2.662 | 4.106 | 8.504 | |
| p | 0.264 | 0.043 | 0.004 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yavuz Temel, G. A Simulation and Empirical Study of Differential Test Functioning (DTF). Psych 2023, 5, 478-496. https://doi.org/10.3390/psych5020032
Yavuz Temel G. A Simulation and Empirical Study of Differential Test Functioning (DTF). Psych. 2023; 5(2):478-496. https://doi.org/10.3390/psych5020032
Chicago/Turabian StyleYavuz Temel, Güler. 2023. "A Simulation and Empirical Study of Differential Test Functioning (DTF)" Psych 5, no. 2: 478-496. https://doi.org/10.3390/psych5020032
APA StyleYavuz Temel, G. (2023). A Simulation and Empirical Study of Differential Test Functioning (DTF). Psych, 5(2), 478-496. https://doi.org/10.3390/psych5020032