Deflagration-to-Detonation Transition in Stochiometric Propane–Hydrogen–Air Mixtures
Abstract
:1. Introduction
2. Materials and Methods
2.1. Test Facility
2.2. Experimental Procedures
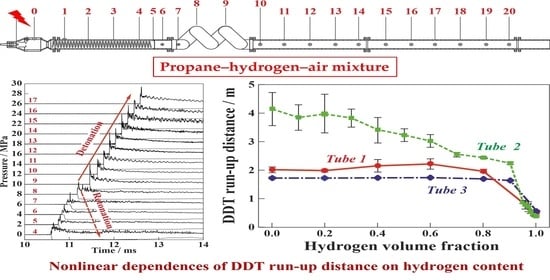
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Shamshin, I.O.; Kazachenko, M.V.; Frolov, S.M.; Basevich, V.Y. Deflagration-to-detonation transition in air mixtures of hydrogen–methane fuel. Combust. Explos. 2020, 13, 60–75. [Google Scholar] [CrossRef]
- Shamshin, I.O.; Kazachenko, M.V.; Frolov, S.M.; Basevich, V.Y. Deflagration-to-detonation transition in stochiometric mixtures of the binary methane–hydrogen fuel with air. Int. J. Hydrogen Energy 2021, 46, 34046–34058. [Google Scholar] [CrossRef]
- Shamshin, I.O.; Kazachenko, M.V.; Frolov, S.M.; Basevich, V.Y. Deflagration-to-detonation transition in air mixtures of ethylene–hydrogen fuel. Combust. Explos. 2021, 14, 26–39. [Google Scholar] [CrossRef]
- Shamshin, I.O.; Kazachenko, M.V.; Frolov, S.M.; Basevich, V.Y. Transition of deflagration to detonation in ethylene-hydrogen-air mixtures. Int. J. Hydrogen Energy 2022, 47, 16676–16685. [Google Scholar] [CrossRef]
- Metghalchi, M.; Keck, J.C. Laminar burning velocity of propane–air mixtures at high temperature and pressure. Combust. Flame 1980, 38, 143–154. [Google Scholar] [CrossRef]
- Bosschaart, K.J.; de Goey, L.P.H.; Burgers, J.M. The laminar burning velocity of flames propagating in mixtures of hydrocarbons and air measured with the heat flux method. Combust. Flame 2004, 136, 261–269. [Google Scholar] [CrossRef]
- Marley, S.K.; Roberts, W.L. Measurements of laminar burning velocity and Markstein number using high-speed chemiluminescence imaging. Combust. Flame 2005, 141, 473–477. [Google Scholar] [CrossRef]
- Huzayyin, A.S.; Moneib, H.A.; Shehatta, M.S.; Attia, A.M.A. Laminar burning velocity and explosion index of LPG–air and propane–air mixtures. Fuel 2008, 87, 39–57. [Google Scholar] [CrossRef]
- Akram, M.; Ratna Kishore, V.; Kumar, S. Laminar burning velocity of propane/CO2/N2–air mixtures at elevated temperatures. Energy Fuels 2012, 26, 5509–5518. [Google Scholar] [CrossRef]
- Dowdy, D.R.; Smith, D.B.; Taylor, S.C.; Williams, A. The use of expanding spherical flames to determine burning velocities and stretch effects in hydrogen/air mixtures. Proc. Combust. Inst. 1991, 23, 325–332. [Google Scholar] [CrossRef]
- Kwon, O.C.; Tseng, L.-K.; Faeth, G.M. Laminar burning velocities and transition to unstable flames in H2/O2/N2 and C3H8/O2/N2 mixtures. Combust. Flame 1992, 90, 230–246. [Google Scholar] [CrossRef] [Green Version]
- Tse, S.D.; Zhu, D.L.; Law, C.K. Morphology and burning rates of expanding spherical flames in H2/O2/inert mixtures up to 60 atmospheres. Proc. Combust. Inst. 2000, 28, 1793–1800. [Google Scholar] [CrossRef] [Green Version]
- Penyazkov, O.G.; Ragotner, K.A.; Dean, A.J.; Varatharajan, B. Autoignition of propane–air mixtures behind reflected shock waves. Proc. Combust. Inst. 2005, 30, 1941–1947. [Google Scholar] [CrossRef]
- Gallagher, S.M.; Curran, H.J.; Metcalfe, W.K.; Healy, D.; Simmie, J.M.; Bourque, G. A rapid compression machine study of the oxidation of propane in the negative temperature coefficient regime. Combust. Flame 2008, 153, 316–333. [Google Scholar] [CrossRef]
- Cheng, R.K.; Oppenheim, A.K. Autoignition in methane–hydrogen mixtures. Combust. Flame 1984, 58, 125–139. [Google Scholar] [CrossRef]
- Keromnes, A.; Metcalfe, W.K.; Heufer, K.A.; Donohoe, N.; Das, A.K.; Sung, C.-J.; Herzler, J.; Naumann, C.; Griebel, P.; Mathieu, O.; et al. An experimental and detailed chemical kinetic modeling study of hydrogen and syngas mixture oxidation at elevated pressures. Combust. Flame 2013, 160, 995–1011. [Google Scholar] [CrossRef] [Green Version]
- Milton, B.E.; Keck, J.C. Laminar burning velocities in stoichiometric hydrogen and hydrogen–hydrocarbon gas mixtures. Combust. Flame 1984, 58, 13–22. [Google Scholar] [CrossRef]
- Yu, G.; Law, C.K.; Wu, C.K. Laminar flame speeds of hydrocarbon–air mixtures with hydrogen addition. Combust. Flame 1986, 63, 339–347. [Google Scholar] [CrossRef] [Green Version]
- Law, C.K.; Kwon, O.C. Effects of hydrocarbon substitution on atmospheric hydrogen–air flame propagation. Int. J. Hydrogen Energy 2004, 29, 867–879. [Google Scholar] [CrossRef]
- Tang, C.; Huang, Z.; Jin, C.; He, J.; Wang, J.; Wang, X.; Miao, H. Laminar burning velocities and combustion characteristics of propane–hydrogen–air premixed flames. Int. J. Hydrogen Energy 2008, 33, 4906–4914. [Google Scholar] [CrossRef]
- Park, O.; Veloo, P.S.; Liu, N.; Egolfopoulos, F.N. Combustion characteristics of alternative gaseous fuels. Proc. Combust. Inst. 2011, 33, 887–894. [Google Scholar] [CrossRef]
- Zhen, H.S.; Cheung, C.S.; Leung, C.W.; Choy, Y.S. Effects of hydrogen concentration on the emission and heat transfer of a premixed LPG-hydrogen flame. Int. J. Hydrogen Energy 2012, 37, 6097–6105. [Google Scholar] [CrossRef]
- Titova, N.S.; Kuleshov, P.S.; Favorskii, O.N.; Starik, A.M. The features of ignition and combustion of composite propane–hydrogen fuel: Modeling study. Int. J. Hydrogen Energy 2014, 39, 6764–6773. [Google Scholar] [CrossRef]
- Man, X.; Tang, C.; Wei, L.; Pan, L.; Huang, Z. Measurements and kinetic study on ignition delay times of propane/hydrogen in argon diluted oxygen. Int. J. Hydrogen Energy 2013, 38, 2523–2530. [Google Scholar] [CrossRef]
- Sevrouk, K.L.; Krivosheyev, P.N.; Penyazkov, O.G.; Torohov, S.A.; Titova, N.S.; Starik, A.M. Numerical and experimental analysis of propane–hydrogen mixture ignition in air. J. Phys. Conf. Ser. 2016, 774, 012083. [Google Scholar] [CrossRef] [Green Version]
- Schwer, D.A.; Kailasanath, K. Towards an assessment of rotating detonation engines with fuel blends. In Proceedings of the 53rd AIAA/SAE/ASEE Joint Propulsion Conference, Atlanta, GA, USA, 10–12 July 2017. AIAA Paper No. 2017-4942. [Google Scholar] [CrossRef]
- Takita, K.; Niioka, T. On detonation behavior of mixed fuels. Shock Waves 1996, 6, 61–66. [Google Scholar] [CrossRef]
- Yoshida, A.; Okuda, Y.; Yatsufusa, T.; Endo, T.; Taki, S.; Aoki, S.; Umeda, Y. Detonation properties of mixed-fuel-and-air gas mixtures. In Proceedings of the 20th International Colloquium on the Dynamics of Explosions and Reactive Systems, McGill University, Montreal, QC, Canada, 31 July–5 August 2005. Paper ICDERS2005-77. [Google Scholar]
- Cheng, G.; Bauer, P.; Zitoun, R. Influence of propane additives on the detonation characteristics of H2-air mixtures. Europ. Phys. J. Appl. Phys. 2014, 65, 30902. [Google Scholar] [CrossRef]
- Yang., Z.; Zhao, K.; Song, X.; Li, B.; Zhang, D.; Xie, L. Effects of mesh aluminium alloys and propane addition on the explosion-suppression characteristics of hydrogen-air mixture. Int. J. Hydrogen Energy 2021, 46, 34998–35013. [Google Scholar] [CrossRef]
- Frolov, S.M.; Shamshin, I.O.; Aksenov, V.S.; Kazachenko, M.V.; Gusev, P.A. Ranking of gaseous fuel–air mixtures according to their detonability using a standard pulsed detonation tube. Combust. Explos. 2019, 12, 78–90. [Google Scholar] [CrossRef]
- Frolov, S.M.; Zvegintsev, V.I.; Aksenov, V.S.; Bilera, I.V.; Kazachenko, M.V.; Shamshin, I.O.; Gusev, P.A.; Belotserkovskaya, M.S. Detonability of fuel–air mixtures. Shock Waves 2020, 30, 721–739. [Google Scholar] [CrossRef]
- Medvedev, S.P.; Polenov, A.N.; Khomik, S.V.; Gel’fand, B.E. Deflagration-to-detonation transition in air-binary fuel mixtures in an obstacle laden channel. Rus. J. Phys. Chem. B 2010, 4, 70–74. [Google Scholar] [CrossRef]
- Cheng, G.; Zitoun, R.; Bauer, P.; Sarrazin, Y. Enhancement and control of deflagration to detonation transition in binary fuels C3H8-H2/air mixtures: Application to propulsion. Aerotec. Missili Spaz. J. Aerosp. Sci Tech. Syst. 2012, 91, 128. [Google Scholar]
- Cheng, G.; Zitoun, R.; Bauer, P.; Sarrazin, Y.; Vidal, P. DDT of the binary fuels H2/C3H8-Air mixtures in the obstructed tube. In Proceedings of the 24th ICDERS, Taipei, Taiwan, 28 July–2 August 2013. [Google Scholar]
- Knystautas, R.; Guirao, C.; Lee, J.H.S. The critical tube diameter for detonation failure in hydrocarbon-air mixtures. Combust. Flame 1982, 48, 63–83. [Google Scholar] [CrossRef]
- Lee, J.H.S. The Detonation Phenomenon; The Cambridge University Press: New York, NY, USA, 2008. [Google Scholar]
- Basevich, V.Y.; Medvedev, S.N.; Frolov, F.S.; Frolov, S.M. Promotion of the high-temperature autoignition of hydrogen–air and methane–air mixtures by normal alkanes. Russ. J. Phys. Chem. B 2015, 9, 250–254. [Google Scholar] [CrossRef]
- Meyer, J.W.; Urtiew, P.A.; Oppenheim, A.K. On the inadequacy of gasdynamic processes for triggering the transition to detonation. Combust. Flame 1970, 14, 13–20. [Google Scholar] [CrossRef]
- Semenov, N.N. Chain Reactions; Goskhimizdat Publishing: Leningrad, Russia, 1934. [Google Scholar]
- Lee, J.H.S.; Knystautas, R.; Freiman, A. High speed turbulent deflagrations and transition to detonation in H2–air mixtures. Combust. Flame 1984, 56, 227–239. [Google Scholar] [CrossRef]
- Shchelkin, K.I. Fast Combustion and Spinning Detonation of Gases; Voenizdat Publishing: Moscow, Russia, 1949. [Google Scholar]
- Basevich, V.Y.; Belyaev, A.A.; Posvyanskii, V.S.; Frolov, S.M. Mechanisms of the oxidation and combustion of normal paraffin hydrocarbons: Transition from C1–C10 to C11–C16. Russ. J. Phys. Chem. B 2013, 7, 161–169. [Google Scholar] [CrossRef]
- Frolov, S.M.; Gel’fand, B.E. Limiting diameter for gas detonation propagation in tubes. Dokl. Acad. Nauk. SSSR 1990, 312, 1177–1180. [Google Scholar]












Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shamshin, I.O.; Kazachenko, M.V.; Frolov, S.M.; Basevich, V.Y. Deflagration-to-Detonation Transition in Stochiometric Propane–Hydrogen–Air Mixtures. Fuels 2022, 3, 667-681. https://doi.org/10.3390/fuels3040040
Shamshin IO, Kazachenko MV, Frolov SM, Basevich VY. Deflagration-to-Detonation Transition in Stochiometric Propane–Hydrogen–Air Mixtures. Fuels. 2022; 3(4):667-681. https://doi.org/10.3390/fuels3040040
Chicago/Turabian StyleShamshin, Igor O., Maxim V. Kazachenko, Sergey M. Frolov, and Valentin Y. Basevich. 2022. "Deflagration-to-Detonation Transition in Stochiometric Propane–Hydrogen–Air Mixtures" Fuels 3, no. 4: 667-681. https://doi.org/10.3390/fuels3040040
APA StyleShamshin, I. O., Kazachenko, M. V., Frolov, S. M., & Basevich, V. Y. (2022). Deflagration-to-Detonation Transition in Stochiometric Propane–Hydrogen–Air Mixtures. Fuels, 3(4), 667-681. https://doi.org/10.3390/fuels3040040