Interactions of Low-Energy Muons with Silicon: Numerical Simulation of Negative Muon Capture and Prospects for Soft Errors
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials Properties
2.2. Muons in the Atmosphere and Flux at the Sea Level
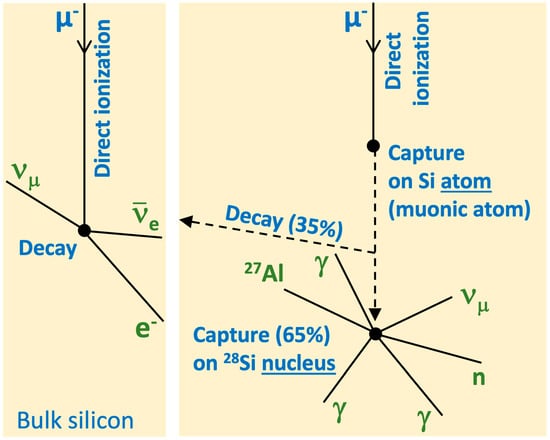
2.3. Interactions of Muons with Silicon
2.3.1. Direct Ionization of Muons in Silicon
2.3.2. Capture of Low-Energy Muon in Silicon
2.4. Calculation of LET and Range for Low-Energy Muons
2.5. Geant4 Simulation Details
3. Results
3.1. Muons LET and Range in Silicon
3.2. Capture of Low-Energy Negative Muons in Silicon
3.2.1. Case of a Pure 28Si Target
3.2.2. Case of Natural Silicon
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Grupen, C.; Shwartz, B. Particle Detectors, 2nd ed.; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Autran, J.L.; Munteanu, D. Soft Errors: From Particles to Circuits; Taylor & Francis/CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Sierawski, B.D.; Mendenhall, M.H.; Reed, R.A.; Clemens, M.A.; Weller, R.A.; Schrimpf, R.D.; Blackmore, E.W.; Trinczek, M.; Hitti, B.; Pellish, J.A.; et al. Muon-Induced Single Event Upsets in Deep-Submicron Technology. IEEE Trans. Nucl. Sci. 2010, 57, 3273–3278. [Google Scholar] [CrossRef]
- Manabe, S.; Watanabe, Y.; Liao, W.; Hashimoto, M.; Nakano, K.; Sato, H.; Kin, T.; Abe, S.-I.; Hamada, K.; Tampo, M.; et al. Negative and Positive Muon-Induced Single Event Upsets in 65-nm UTBB SOI SRAMs. IEEE Trans. Nucl. Sci. 2018, 65, 1742–1749. [Google Scholar] [CrossRef]
- Liao, W.; Hashimoto, M.; Manabe, S.; Watanabe, Y.; Abe, S.-I.; Nakano, K.; Sato, H.; Kin, T.; Hamada, K.; Tampo, M.; et al. Measurement and Mechanism Investigation of Negative and Positive Muon-Induced Upsets in 65-nm Bulk SRAMs. IEEE Trans. Nucl. Sci. 2018, 65, 1734–1741. [Google Scholar] [CrossRef]
- Hashimoto, M.; Kobayashi, K.; Furuta, J.; Abe, S.-I.; Watanabe, Y. Characterizing SRAM and FF soft error rates with measurement and simulation. Integration 2019, 69, 161–179. [Google Scholar] [CrossRef]
- Kato, T.; Tampo, M.; Takeshita, S.; Tanaka, H.; Matsuyama, H.; Hashimoto, M.; Miyake, Y. Muon-Induced Single-Event Upsets in 20-nm SRAMs: Comparative Characterization with Neutrons and Alpha Particles. IEEE Trans. Nucl. Sci. 2021, 68, 1436–1444. [Google Scholar] [CrossRef]
- Smith, A.R.; McDonald, R.J.; Hurley, D.L.; Holland, S.E.; Groom, D.E.; Brown, W.E.; Gilmore, D.K.; Stover, R.J.; Wei, M. Radiation events in astronomical CCD images. In Proceedings of the SPIE 4669, San Jose, CA, USA, 19–25 January 2002; pp. 172–183. [Google Scholar]
- Saad Saoud, T.; Moindjie, S.; Autran, J.L.; Munteanu, D.; Wrobel, F.; Saigné, F.; Cocquerez, P.; Dilillo, L.M.; Glorieux, M. Use of CCD to Detect Terrestrial Cosmic Rays at Ground Level: Altitude vs. Underground Experiments, Modeling and Numerical Monte Carlo Simulation. IEEE Trans. Nucl. Sci. 2014, 61, 3380–3388. [Google Scholar] [CrossRef]
- Saad Saoud, T.; Moindjie, S.; Munteanu, D.; Autran, J.L. Natural radiation events in CCD imagers at ground level. Microelectron. Reliab. 2016, 64, 68–72. [Google Scholar] [CrossRef]
- Sierawski, B.D.; Reed, R.A.; Mendenhall, M.H.; Weller, R.A.; Schrimpf, R.D.; Wen, S.-J.; Wong, R.; Tam, N.; Baumann, R.C. Effects of scaling on muon-induced soft errors. In Proceedings of the IEEE International Reliability Physics Symposium, Monterey, CA, USA, 10–14 April 2011; pp. 3C.3.1–3C.3.6. [Google Scholar]
- Sierawski, B.D.; Bhuva, B.; Reed, R.; Tam, N.; Narasimham, B.; Ishida, K.; Hillier, A.; Trinczek, M.; Blackmore, E.; Wen, S.-J.; et al. Bias dependence of muon-induced single event upsets in 28 nm static random-access memories. In Proceedings of the IEEE International Reliability Physics Symposium, Waikoloa, HI, USA, 1–5 June 2014; pp. 2B.2.1–2B.2.5. [Google Scholar]
- Blundell, S.J.; De Renzi, R.; Lancaster, T.L.; Pratt, F.L. Muon Spectroscopy: An Introduction; Oxford University Press: Oxford, UK, 2021. [Google Scholar]
- Hillier, A.D.; Blundell, S.J.; McKenzie, I.; Umegaki, I.; Shu, L.; Wright, J.A.; Prokscha, T.; Bert, F.; Shimomura, K.; Berlie, A.; et al. Muon spin spectroscopy. Nat. Rev. Methods Primers 2022, 2, 4. [Google Scholar] [CrossRef]
- Blackmore, E.W.; Stukel, M.; Trinczek, M.; Slayman, C.; Wen, S.-J.; Wong, R. Terrestrial Muon Flux Measurement at Low Energies for Soft Error Studies. IEEE Trans. Nucl. Sci. 2015, 62, 2792–2796. [Google Scholar] [CrossRef]
- Serre, S.; Semikh, S.; Autran, J.L.; Munteanu, D.; Gasiot, G.; Roche, P. Effects of Low Energy Muons on Electronics: Physical Insights and Geant4 Simulation. In Proceedings of the European Workshop on Radiation and Its Effects on Components and Systems, Biarritz, France, 24–28 September 2012. [Google Scholar]
- Ziegler, J.F.; Lanford, W.A. Effect of cosmic rays on computer memories. Science 1979, 206, 776–788. [Google Scholar] [CrossRef]
- Autran, J.L.; Munteanu, D. Atmospheric Neutron Radiation Response of III-V Binary Compound Semiconductors. IEEE Trans. Nucl. Sci. 2020, 67, 1428–1435. [Google Scholar] [CrossRef]
- EXPACS, Excel-Based Program for Calculating Atmospheric Cosmic-ray Spectrum. Available online: https://phits.jaea.go.jp/expacs/ (accessed on 20 October 2023).
- Beringer, J.; Arguin, J.-F.; Barnett, R.M.; Copic, K.; Dahl, O.; Groom, D.E.; Lin, C.-J.; Lys, J.; Murayama, H.; Wohl, C.G.; et al. (Particle Data Group). The Review of Particle Physics. Phys. Rev. D 2012, 86, 010001. [Google Scholar] [CrossRef]
- Cecchini, S.; Spurio, M. Atmospheric muons: Experimental aspects. Geosci. Instrum. Methods Data Syst. 2012, 1, 185–196. [Google Scholar] [CrossRef]
- Grieder, P.K.F. Cosmic Rays at Earth; Elsevier Press: Amsterdam, The Netherlands, 2001. [Google Scholar]
- Akkerman, A.; Barak, J.; Yitzhak, N.M. Role of Elastic Scattering of Protons, Muons, and Electrons in Inducing Single-Event Upsets. IEEE Trans. Nucl. Sci. 2017, 64, 2648–2660. [Google Scholar] [CrossRef]
- Munteanu, D.; Autran, J.L. Modeling and Simulation of Single-Event Effects in Digital Devices and ICs. IEEE Trans. Nucl. Sci. 2008, 55, 1854–1878. [Google Scholar] [CrossRef]
- Mukhopadhyay, N.C. Nuclear Muon Capture. Phys. Rep. 1977, 30, 1–144. [Google Scholar] [CrossRef]
- Knecht, A.; Skawran, A.; Vogiatzi, S.M. Study of nuclear properties with muonic atoms. Eur. Phys. J. Plus 2020, 135, 777. [Google Scholar] [CrossRef]
- Fermi, E.; Teller, E. The capture of negative mesotrons in matter. Phys. Rev. 1947, 72, 399–408. [Google Scholar] [CrossRef]
- Suzuki, T.; Measday, D.F.; Roalsvig, J.P. Total nuclear capture rates for negative muons. Phys. Rev. C 1987, 35, 2212–2224. [Google Scholar] [CrossRef]
- Tiomno, J.; Wheeler, J.A. Charge-exchange reaction of the μ-meson with the nucleus. Rev. Mod. Phys. 1949, 21, 153–165. [Google Scholar] [CrossRef]
- Singer, P. Emission of particles following muon capture in intermediate and heavy nuclei. Nucl. Phys. Springer Tracts Mod. Phys. 1974, 71, 39–87. [Google Scholar]
- Measday, D.F. The nuclear physics of muon capture. Phys. Rep. 2001, 354, 243–409. [Google Scholar] [CrossRef]
- Measday, D.F.; Stocki, T.J.; Moftah, B.A.; Tam, H. g rays from muon capture 27Al and natural Si. Phys. Rev. C 2007, 76, 035504. [Google Scholar] [CrossRef]
- Sundelin, R.M.; Edelstein, R.M.; Suzuki, A.; Takahashi, K. Spectrum of neutrons from muon capture in silicon, sulfur, and calcium. Phys. Rev. Lett. 1968, 20, 1198–1200. [Google Scholar] [CrossRef]
- Sobottka, S.E.; Wills, E.L. Energy spectrum of charged particles emitted following muon capture in 28Si. Phys. Rev. Lett. 1968, 20, 596. [Google Scholar] [CrossRef]
- Tang, H.H.K. SEMM-2: A new generation of single-event-effect modeling tools. IBM J. Res. Dev. 2008, 52, 233–244. [Google Scholar] [CrossRef]
- Tiesinga, E.; Mohr, P.; Newell, D.; Taylor, B. CODATA recommended values of the fundamental physical constants: 2018. Rev. Mod. Phys. 2021, 93, 025010. [Google Scholar] [CrossRef] [PubMed]
- Senba, M.; Arseneau, D.J.; Pan, J.J.; Fleming, D.G. Slowing-down times and stopping powers for ~2−MeV μ+ in low-pressure gases. Phys. Rev. A 2006, 74, 042708. [Google Scholar] [CrossRef]
- Ziegler, J.F.; Ziegler, M.D.; Biersack, J.P. SRIM—The stopping and range of ions in matter. Nucl. Instrum. Meth. B 2010, 268, 1818–1823. [Google Scholar] [CrossRef]
- SRIM. The Stopping and Range of Ions in Matter. Available online: http://srim.org (accessed on 20 October 2023).
- Agostinelli, S.; Allison, J.; Amako, K.; Apostolakis, J.; Araujo, H.; Arce, P.; Asai, M.; Axen, D.; Banerjee, S.; Barrand, G.; et al. Geant4—A simulation toolkit. Nucl. Instrum. Meth. A 2003, 506, 250–303. [Google Scholar] [CrossRef]
- Allison, J.K.; Amako, K.; Apostolakis, J.; Araujo, H.; Arce Dubois, P.; Asai, M.G.; Barrand, G.R.; Capra, R.S.; Chauvie, S.; Chytraceket, R.; et al. Geant4 developments and applications. IEEE Trans. Nucl. Sci. 2006, 53, 270–278. [Google Scholar] [CrossRef]
- Allison, J.; Amako, K.; Apostolakis, J.; Arce, P.; Asai, M.; Aso, T.; Bagli, E.; Bagulya, A.; Banerjee, S.; Barrand, G.; et al. Recent developments in Geant4. Nucl. Instrum. Meth. A 2016, 835, 186–225. [Google Scholar] [CrossRef]
- Martinie, S.; Saad-Saoud, T.; Moindjie, S.; Munteanu, D.; Autran, J.L. Behavioral modeling of SRIM tables for numerical simulation. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. At. 2014, 322, 2–6. [Google Scholar] [CrossRef]
- Budyashov, Y.G.; Zinov, V.G.; Konin, A.D.; Mukhin, A.I.; Chatrchyan, A.M. Charged Particles from the Capture of Negative Muons by the Nuclei 28Si, 32S, 40Ca, and 64Cu. Sov. J. Exp. Theor. Phys. 1971, 33, 11. [Google Scholar]
- Macdonald, B.; Diaz, J.A.; Kaplan, S.N.; Pyle, R.V. Neutrons from Negative-Muon Capture. Phys. Rev. 1965, 139, B1253–B1263. [Google Scholar] [CrossRef]
- Sundelin, R.M.; Edelstein, R.M. Neutron Asymmetries and Energy Spectra from Muon Capture in Si, S, and Ca. Phys. Rev. C 1973, 7, 1037–1060. [Google Scholar] [CrossRef]
- Wyttenbach, A.; Baertschi, P.; Bajo, S.; Hadermann, J.; Junker, K.; Katcoff, S.; Hermes, E.A.; Pruys, H.S. Probabilities of muon induced nuclear reactions involving charged particle emission. Nucl. Phys. A 1978, 294, 278–292. [Google Scholar] [CrossRef]
- King, M.P.; Reed, R.A.; Weller, R.A.; Mendenhall, M.H.; Schrimpf, R.D.; Alles, M.L.; Auden, E.C.; Armstrong, S.E.; Asai, M. The Impact of Delta-Rays on Single-Event Upsets in Highly Scaled SOI SRAMs. IEEE Trans. Nucl. Sci. 2010, 57, 3169–3175. [Google Scholar] [CrossRef]
- JESD89B; Measurement and Reporting of Alpha Particle and Terrestrial Cosmic Ray-Induced Soft Errors in Semiconductor Devices. Revision of JESD89A; JEDEC: Arlington, VA, USA, 2021.
- Gaillard, R. Single Event Effects: Mechanisms and Classification. In Soft Errors in Modern Electronic Systems; Nicolaidis, M., Ed.; Springer: New York, NY, USA, 2011. [Google Scholar]
- Roche, P.; Autran, J.L.; Gasiot, G.; Munteanu, D. Technology downscaling worsening radiation effects in bulk: SOI to the rescue. In Proceedings of the IEEE International Electron Device Meeting, Washington, DC, USA, 9–11 December 2013; pp. 766–769. [Google Scholar]
- Fang, Y.-P.; Oates, A.S. Muon-Induced Soft Errors in SRAM Circuits in the Terrestrial Environment. IEEE Trans. Device Mater. Reliab. 2015, 15, 115–122. [Google Scholar] [CrossRef]
- Seifert, N.; Jahinuzzaman, S.; Velamala, J.; Patel, N. Susceptibility of planar and 3D tri-gate technologies to muon-induced single event upsets. In Proceedings of the IEEE International Reliability Physics Symposium, Monterey, CA, USA, 19–23 April 2015; pp. 2C.1.1–2C.1.6. [Google Scholar]











| Symbol | Atomic Number | Isotope | Natural Abundance |
|---|---|---|---|
| Si | 14 | 28Si | 92.20% |
| 29Si | 4.70% | ||
| 30Si | 3.10% |
| Semiconductor | Bandgap @ 300 K Eg (eV) | Number of Atoms per cm3 (×1022) | Density (g/cm3) | Electron–Hole Pair Creation Energy Eeh (eV) |
|---|---|---|---|---|
| Si | 1.124 | 5.0 | 2.329 | 3.6 |
| i | pi | qi |
|---|---|---|
| 1 | −0.30049 | −0.36483 |
| 2 | 3.63833 | 2.16872 |
| 3 | −8.04761 | −2.59854 |
| 4 | 1.00000 | 1.74777 |
| 5 | −7.58899 | −6.8565 × 10−1 |
| 6 | 3.69887 | 1.6021 × 10−1 |
| 7 | −1.19032 | −2.188 × 10−2 |
| 8 | 2.5518 × 10−1 | 1.612 × 10−3 |
| 9 | −3.604 × 10−2 | −4.94 × 10−5 |
| 10 | 3.219 × 10−3 | −9.69882 |
| 11 | −1.65 × 10−4 | - |
| 12 | 3.69 × 10−6 | - |
| 13 | −1.93759 | - |
| Type of Mechanism | 28Si | 29Si | 30Si | Natural Si |
|---|---|---|---|---|
| Muon decay | 34.30% | 40.55% | 44.28% | 34.80% |
| Muon nuclear capture | 65.70% | 59.45% | 55.72% | 65.20% |
| Secondary | Energy (MeV) | Event Start Time | Event Mechanism |
|---|---|---|---|
| e- | 2.801 keV | 0.1024 ps | Muon atomic capture and cascade down to the ground state accompanied by γ-ray emission. * Energy for transition Lα (3d → 2p) # Energy for transition Kα (2p → 1s) |
| gamma | 12.45 keV | ||
| e- | 6.709 keV | ||
| gamma | 12.35 keV | ||
| gamma | 26.68 keV | ||
| gamma | 76.24 keV * | ||
| gamma | 386.8 keV # | ||
| nu_mu | 84.49 MeV | 873 ns | |
| neutron | 782.1 keV | 874 ns | 28Al* nucleus evaporation |
| Al27 | 288.4 keV | ||
| gamma | 3.013 MeV | ||
| gamma | 2.668 MeV | ||
| gamma | 1.017 MeV |
| Total per Secondary Heavy Fragments Produced | Muon Capture Reaction in 28Si | Yield (%) |
|---|---|---|
| 15.51 | ||
| Al | 46.68 | |
| 75.48% | 13.26 | |
| 0.03 | ||
| 1.77 | ||
| 8.09 | ||
| Mg | 0.52 | |
| 16.33% | 5.41 | |
| 0.54 | ||
| 0.22 | ||
| Na | 1.90 | |
| 6.57% | 3.18 | |
| 0.72 | ||
| Other reactions with emission of Na isotopes | 0.55 | |
| Other | 0.76 | |
| 1.62% | 0.26 | |
| Other reactions | 0.60 | |
| Total | 100.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Autran, J.-L.; Munteanu, D. Interactions of Low-Energy Muons with Silicon: Numerical Simulation of Negative Muon Capture and Prospects for Soft Errors. J. Nucl. Eng. 2024, 5, 91-110. https://doi.org/10.3390/jne5010007
Autran J-L, Munteanu D. Interactions of Low-Energy Muons with Silicon: Numerical Simulation of Negative Muon Capture and Prospects for Soft Errors. Journal of Nuclear Engineering. 2024; 5(1):91-110. https://doi.org/10.3390/jne5010007
Chicago/Turabian StyleAutran, Jean-Luc, and Daniela Munteanu. 2024. "Interactions of Low-Energy Muons with Silicon: Numerical Simulation of Negative Muon Capture and Prospects for Soft Errors" Journal of Nuclear Engineering 5, no. 1: 91-110. https://doi.org/10.3390/jne5010007
APA StyleAutran, J. -L., & Munteanu, D. (2024). Interactions of Low-Energy Muons with Silicon: Numerical Simulation of Negative Muon Capture and Prospects for Soft Errors. Journal of Nuclear Engineering, 5(1), 91-110. https://doi.org/10.3390/jne5010007