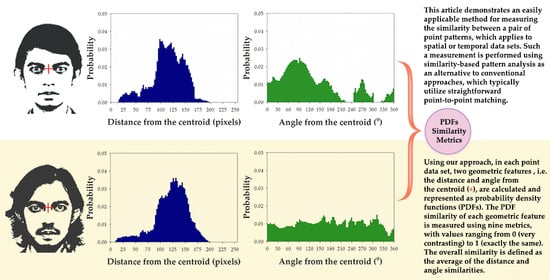
Figure 1.
We compared the spatial pattern similarity of two point data sets by measuring PDF similarities for the distance (δ) and angle (θ) from the centroid of the extent (red cross) to each point of each data set (a,b).
Figure 1.
We compared the spatial pattern similarity of two point data sets by measuring PDF similarities for the distance (δ) and angle (θ) from the centroid of the extent (red cross) to each point of each data set (a,b).
Figure 2.
We compared the temporal pattern similarity of two time-series data sets by measuring the similarity of the PDFs of distance (δ) and angle (θ) from the centroid of the graphs where all time-series data sets under comparison were plotted (red cross) to each point within the pair of time series data sets (a,b).
Figure 2.
We compared the temporal pattern similarity of two time-series data sets by measuring the similarity of the PDFs of distance (δ) and angle (θ) from the centroid of the graphs where all time-series data sets under comparison were plotted (red cross) to each point within the pair of time series data sets (a,b).
Figure 3.
Two pairs of hypothetical PDFs: PDFs (
a,
b) represent very contrasting pairs of PDFs, while PDFs (
c,
d) represent exactly matching PDFs. We selected nine metrics out of the 45 metrics reviewed in [
29], where the nine selected metrics resulted in a similarity of 0 for (
a,
b) and a similarity of 1 for (
c,
d).
Figure 3.
Two pairs of hypothetical PDFs: PDFs (
a,
b) represent very contrasting pairs of PDFs, while PDFs (
c,
d) represent exactly matching PDFs. We selected nine metrics out of the 45 metrics reviewed in [
29], where the nine selected metrics resulted in a similarity of 0 for (
a,
b) and a similarity of 1 for (
c,
d).
Figure 4.
Overall workflow of the proposed method for measuring spatial and temporal pattern similarity between pairs of data sets.
Figure 4.
Overall workflow of the proposed method for measuring spatial and temporal pattern similarity between pairs of data sets.
Figure 5.
Two pairs of hypothetical spatial patterns used for evaluating the method in terms of its sensibility. With regard to the geometric features used in this study—namely, the distance (δ) and angle (θ) from the centroid to each point within each pair—the method should result in relatively high PDF similarity of δ but relatively low PDF similarity of θ for the eagle pair (a,b), and vice versa for the turtle pair (c,d). The red cross is the centroid of the extent.
Figure 5.
Two pairs of hypothetical spatial patterns used for evaluating the method in terms of its sensibility. With regard to the geometric features used in this study—namely, the distance (δ) and angle (θ) from the centroid to each point within each pair—the method should result in relatively high PDF similarity of δ but relatively low PDF similarity of θ for the eagle pair (a,b), and vice versa for the turtle pair (c,d). The red cross is the centroid of the extent.
Figure 6.
A pair of hypothetical mirrored eagle patterns at original resolution (a,b) and their resampled patterns at a 20× coarser resolution (c,d). These hypothetical data sets were used to evaluate the method in terms of its sensitivity to changes in resolution.
Figure 6.
A pair of hypothetical mirrored eagle patterns at original resolution (a,b) and their resampled patterns at a 20× coarser resolution (c,d). These hypothetical data sets were used to evaluate the method in terms of its sensitivity to changes in resolution.
Figure 7.
A hypothetical reference deforestation time-series (red squares) was shifted to the left from 16 days to 80 days (grey squares)—representing an acceleration of detection—to perform sensitivity analyses of the proposed method in terms of its robustness to measure the similarity of temporal patterns. The blue cross is the centroid of the graph.
Figure 7.
A hypothetical reference deforestation time-series (red squares) was shifted to the left from 16 days to 80 days (grey squares)—representing an acceleration of detection—to perform sensitivity analyses of the proposed method in terms of its robustness to measure the similarity of temporal patterns. The blue cross is the centroid of the graph.
Figure 8.
Deforestation hotspots (red) for 2020 derived from Landsat-8 OLI imagery.
Figure 8.
Deforestation hotspots (red) for 2020 derived from Landsat-8 OLI imagery.
Figure 9.
PDFs of angle from the centroid to each point (θ) for each pair of hypothetical patterns shown in
Figure 5: (
a,
b) the pair of eagle patterns and (
c,
d) the pair of turtle patterns.
Figure 9.
PDFs of angle from the centroid to each point (θ) for each pair of hypothetical patterns shown in
Figure 5: (
a,
b) the pair of eagle patterns and (
c,
d) the pair of turtle patterns.
Figure 10.
PDFs of distance from the centroid to each point (δ) for each pair of hypothetical patterns shown in
Figure 5: (
a,
b) pair of eagle patterns and (
c,
d) pair of turtle patterns.
Figure 10.
PDFs of distance from the centroid to each point (δ) for each pair of hypothetical patterns shown in
Figure 5: (
a,
b) pair of eagle patterns and (
c,
d) pair of turtle patterns.
Figure 11.
PDF similarity of angle from the centroid of origin to each point (θ) of two hypothetical shapes: (a) circle with diameter of about 1.0567 m, and (b) square with dimensions of 1.0567 × 1.0567 m2, due to shifting from the origin in all directions. Green crosses indicate similarity of θ from all nine metrics. Red lines on the upper edge of the envelopes indicate the similarity of θ using the Fidelity metric. Blue lines on the lower edge of the envelopes indicate the similarity of θ using the Soergel–Ruzicka–Tanimoto metric.
Figure 11.
PDF similarity of angle from the centroid of origin to each point (θ) of two hypothetical shapes: (a) circle with diameter of about 1.0567 m, and (b) square with dimensions of 1.0567 × 1.0567 m2, due to shifting from the origin in all directions. Green crosses indicate similarity of θ from all nine metrics. Red lines on the upper edge of the envelopes indicate the similarity of θ using the Fidelity metric. Blue lines on the lower edge of the envelopes indicate the similarity of θ using the Soergel–Ruzicka–Tanimoto metric.
Figure 12.
PDF similarity of distance from the centroid of origin to each point (δ) of two hypothetical shapes: (a) circle with diameter of about 1.0567 m, and (b) square with dimensions of 1.0567 × 1.0567 m2, due to shifting from the origin in all directions. Green crosses indicate the similarity of θ from all nine metrics. Red lines on the upper edge of the envelopes indicate the similarity of δ using the Fidelity metric. Blue lines on the lower edge of the envelopes indicate the similarity of δ using the metric of Soergel–Ruzicka–Tanimoto.
Figure 12.
PDF similarity of distance from the centroid of origin to each point (δ) of two hypothetical shapes: (a) circle with diameter of about 1.0567 m, and (b) square with dimensions of 1.0567 × 1.0567 m2, due to shifting from the origin in all directions. Green crosses indicate the similarity of θ from all nine metrics. Red lines on the upper edge of the envelopes indicate the similarity of δ using the Fidelity metric. Blue lines on the lower edge of the envelopes indicate the similarity of δ using the metric of Soergel–Ruzicka–Tanimoto.
Figure 13.
Overall spatial pattern similarity (i.e., the average of similarity of θ and similarity of δ) for two hypothetical shapes: (a) circle with diameter of about 1.0567 m, and (b) square with dimensions of 1.0567 × 1.0567 m2, due to shifting from the origin in all directions. Green crosses indicate overall similarity from all nine metrics. Red lines on the upper edge of the envelopes indicate the overall similarity using the Fidelity metric. Blue lines on the lower edge of the envelopes indicate the overall similarity using the metric of Soergel–Ruzicka–Tanimoto.
Figure 13.
Overall spatial pattern similarity (i.e., the average of similarity of θ and similarity of δ) for two hypothetical shapes: (a) circle with diameter of about 1.0567 m, and (b) square with dimensions of 1.0567 × 1.0567 m2, due to shifting from the origin in all directions. Green crosses indicate overall similarity from all nine metrics. Red lines on the upper edge of the envelopes indicate the overall similarity using the Fidelity metric. Blue lines on the lower edge of the envelopes indicate the overall similarity using the metric of Soergel–Ruzicka–Tanimoto.
Figure 14.
Overall spatial pattern similarity (i.e., the average of similarity of θ and similarity of δ) of various pairs of hypothetical shapes with different resolutions: (
a) eagle pattern (shown in
Figure 6a) compared with itself at different resolutions, ranging from 1× to 20× coarser; (
b) eagle pattern (shown in
Figure 6b) compared with itself at different resolutions, ranging from 1× to 20× coarser; and (
c) eagle pattern (shown in
Figure 6a) compared with its mirrored pattern (shown in
Figure 6b) at different resolutions, ranging from 1× to 20× coarser. Green crosses indicate overall similarity from all nine metrics. Red lines on the upper edge of the envelopes indicate the overall similarity using the Fidelity metric. Blue lines on the lower edge of the envelopes indicate the overall similarity using the metric of Soergel–Ruzicka–Tanimoto.
Figure 14.
Overall spatial pattern similarity (i.e., the average of similarity of θ and similarity of δ) of various pairs of hypothetical shapes with different resolutions: (
a) eagle pattern (shown in
Figure 6a) compared with itself at different resolutions, ranging from 1× to 20× coarser; (
b) eagle pattern (shown in
Figure 6b) compared with itself at different resolutions, ranging from 1× to 20× coarser; and (
c) eagle pattern (shown in
Figure 6a) compared with its mirrored pattern (shown in
Figure 6b) at different resolutions, ranging from 1× to 20× coarser. Green crosses indicate overall similarity from all nine metrics. Red lines on the upper edge of the envelopes indicate the overall similarity using the Fidelity metric. Blue lines on the lower edge of the envelopes indicate the overall similarity using the metric of Soergel–Ruzicka–Tanimoto.
Figure 15.
Sensitivity of the method on hypothetical temporal deforestation data sets, due to: (a) acceleration; (b) delay; (c) overestimation; and (d) underestimation of deforestation detection, compared to the reference. Green crosses indicate overall similarity (i.e., the average of similarity of θ and similarity of δ) from all nine metrics. Red lines on the upper edge of the envelopes indicate the overall similarity using the Fidelity metric. Blue lines on the lower edge of the envelopes indicate the overall similarity using the metric of Soergel–Ruzicka–Tanimoto.
Figure 15.
Sensitivity of the method on hypothetical temporal deforestation data sets, due to: (a) acceleration; (b) delay; (c) overestimation; and (d) underestimation of deforestation detection, compared to the reference. Green crosses indicate overall similarity (i.e., the average of similarity of θ and similarity of δ) from all nine metrics. Red lines on the upper edge of the envelopes indicate the overall similarity using the Fidelity metric. Blue lines on the lower edge of the envelopes indicate the overall similarity using the metric of Soergel–Ruzicka–Tanimoto.
Figure 16.
Overall similarity (i.e., the average of θ and δ similarities) of the spatial pattern between deforestation hotspots in Indonesia in 2020, derived from Landsat-8 OLI (at clarity ≥50% and deforestation intensity ≥50%) and deforestation hotspots in Indonesia in 2020 derived from MODIS (at change-detection thresholds ranging from 50 to 130). Green crosses indicate overall similarity from all nine metrics. Red lines on the upper edge of the envelopes indicate the overall similarity using the Fidelity metric. Blue lines on the lower edge of the envelopes indicate the overall similarity using the metric of Soergel–Ruzicka–Tanimoto.
Figure 16.
Overall similarity (i.e., the average of θ and δ similarities) of the spatial pattern between deforestation hotspots in Indonesia in 2020, derived from Landsat-8 OLI (at clarity ≥50% and deforestation intensity ≥50%) and deforestation hotspots in Indonesia in 2020 derived from MODIS (at change-detection thresholds ranging from 50 to 130). Green crosses indicate overall similarity from all nine metrics. Red lines on the upper edge of the envelopes indicate the overall similarity using the Fidelity metric. Blue lines on the lower edge of the envelopes indicate the overall similarity using the metric of Soergel–Ruzicka–Tanimoto.
Figure 17.
Overall similarity (i.e., the average of similarity of θ and similarity of δ) of temporal pattern between deforestation hotspots in Indonesia in 2020, derived from Landsat-8 OLI at clarity ≥50% and deforestation intensity ≥50%, and deforestation hotspots in Indonesia in 2020, derived from MODIS at change-detection thresholds ranging from 50 to 130. Green crosses indicate overall similarity from all nine metrics. Red lines on the upper edge of the envelopes indicate overall similarity using metric of Fidelity. Blue lines on the upper edge of the envelopes indicate overall similarity using metric of Soergel–Ruzicka–Tanimoto.
Figure 17.
Overall similarity (i.e., the average of similarity of θ and similarity of δ) of temporal pattern between deforestation hotspots in Indonesia in 2020, derived from Landsat-8 OLI at clarity ≥50% and deforestation intensity ≥50%, and deforestation hotspots in Indonesia in 2020, derived from MODIS at change-detection thresholds ranging from 50 to 130. Green crosses indicate overall similarity from all nine metrics. Red lines on the upper edge of the envelopes indicate overall similarity using metric of Fidelity. Blue lines on the upper edge of the envelopes indicate overall similarity using metric of Soergel–Ruzicka–Tanimoto.
Figure 18.
Overall spatial pattern similarity (i.e., the average of similarity of θ and similarity of δ) of two hypothetical shapes: (a) circle with diameter of about 1.0567 m and (b) square with dimensions of 1.0567 × 1.0567 m2, due to shifting from the origin in all directions. Green crosses indicate overall similarity from all 10 metrics. Orange lines in the middle of the envelopes indicate overall similarity using the new metric of Ruzicka–Fidelity (Equation (1)). Vertical blue lines indicate half size of the maximum radii of the shapes, while vertical red lines indicate the maximum radii of the shapes.
Figure 18.
Overall spatial pattern similarity (i.e., the average of similarity of θ and similarity of δ) of two hypothetical shapes: (a) circle with diameter of about 1.0567 m and (b) square with dimensions of 1.0567 × 1.0567 m2, due to shifting from the origin in all directions. Green crosses indicate overall similarity from all 10 metrics. Orange lines in the middle of the envelopes indicate overall similarity using the new metric of Ruzicka–Fidelity (Equation (1)). Vertical blue lines indicate half size of the maximum radii of the shapes, while vertical red lines indicate the maximum radii of the shapes.
Figure 19.
Normalized hypothetical time-series data as shown in
Figure 7. Red squares indicate the origin; grey squares indicate left shifts from the origin, representing an acceleration of detection from 16 days to 80 days. The blue cross is the centroid of the graph.
Figure 19.
Normalized hypothetical time-series data as shown in
Figure 7. Red squares indicate the origin; grey squares indicate left shifts from the origin, representing an acceleration of detection from 16 days to 80 days. The blue cross is the centroid of the graph.
Figure 20.
Sensitivity of the method on hypothetical deforestation temporal data sets after normalization, due to possibility of: (a) acceleration, (b) delay, (c) overestimation, and (d) underestimation of deforestation detection, compared to the reference. Green crosses indicate the overall similarity (i.e., the average similarity of θ and similarity of δ) from all nine metrics. Red lines on the upper edge of the envelopes indicate the overall similarity using the Fidelity metric. Blue lines on the lower edge of the envelopes indicate the overall similarity using the metric of Soergel–Ruzicka–Tanimoto.
Figure 20.
Sensitivity of the method on hypothetical deforestation temporal data sets after normalization, due to possibility of: (a) acceleration, (b) delay, (c) overestimation, and (d) underestimation of deforestation detection, compared to the reference. Green crosses indicate the overall similarity (i.e., the average similarity of θ and similarity of δ) from all nine metrics. Red lines on the upper edge of the envelopes indicate the overall similarity using the Fidelity metric. Blue lines on the lower edge of the envelopes indicate the overall similarity using the metric of Soergel–Ruzicka–Tanimoto.
Figure 21.
Interpolated hypothetical deforestation time-series data shown in
Figure 7 at a time slice of a 1-day interval. Red squares indicate the original time-series; grey squares indicate left shifts from the original, representing an acceleration on detection from 16 days to 80 days. The blue cross is the centroid of the graph.
Figure 21.
Interpolated hypothetical deforestation time-series data shown in
Figure 7 at a time slice of a 1-day interval. Red squares indicate the original time-series; grey squares indicate left shifts from the original, representing an acceleration on detection from 16 days to 80 days. The blue cross is the centroid of the graph.
Figure 22.
Sensitivity of the method on hypothetical temporal data sets on deforestation after interpolation at a time slice of 1 day, due to the possibility of (a) acceleration, (b) delay, (c) overestimation, and (d) underestimation of deforestation detection, compared to the reference. Green crosses indicate overall similarity (i.e., the average of θ and δ similarities) from all nine metrics. Red lines on the upper edge of the envelopes indicate the overall similarity using the Fidelity metric. Blue lines on the lower edge of the envelopes indicate the overall similarity using the metric of Soergel–Ruzicka–Tanimoto.
Figure 22.
Sensitivity of the method on hypothetical temporal data sets on deforestation after interpolation at a time slice of 1 day, due to the possibility of (a) acceleration, (b) delay, (c) overestimation, and (d) underestimation of deforestation detection, compared to the reference. Green crosses indicate overall similarity (i.e., the average of θ and δ similarities) from all nine metrics. Red lines on the upper edge of the envelopes indicate the overall similarity using the Fidelity metric. Blue lines on the lower edge of the envelopes indicate the overall similarity using the metric of Soergel–Ruzicka–Tanimoto.
Figure 23.
Sensitivity of the method on hypothetical temporal data sets on deforestation after interpolation at a time slice of 1 h, due to the possibility of (a) acceleration, (b) delay, (c) overestimation, and (d) underestimation of deforestation detection, compared to the reference. Green crosses indicate overall similarity (i.e., the average of θ and δ similarities) from all nine metrics. Red lines on the upper edge of the envelopes indicate the overall similarity using the Fidelity metric. Blue lines on the lower edge of the envelopes indicate the overall similarity using the metric of Soergel–Ruzicka–Tanimoto.
Figure 23.
Sensitivity of the method on hypothetical temporal data sets on deforestation after interpolation at a time slice of 1 h, due to the possibility of (a) acceleration, (b) delay, (c) overestimation, and (d) underestimation of deforestation detection, compared to the reference. Green crosses indicate overall similarity (i.e., the average of θ and δ similarities) from all nine metrics. Red lines on the upper edge of the envelopes indicate the overall similarity using the Fidelity metric. Blue lines on the lower edge of the envelopes indicate the overall similarity using the metric of Soergel–Ruzicka–Tanimoto.
Figure 24.
Sensitivity of the method on hypothetical temporal data sets on deforestation after interpolation at a time slice of 1 min, due to the possibility of (a) acceleration, (b) delay, (c) overestimation, and (d) underestimation of deforestation detection, compared to the reference. Green crosses indicate overall similarity (i.e., the average of θ and δ similarities) from all nine metrics. Red lines on the upper edge of the envelopes indicate the overall similarity using the Fidelity metric. Blue lines on the lower edge of the envelopes indicate the overall similarity using the metric of Soergel–Ruzicka–Tanimoto.
Figure 24.
Sensitivity of the method on hypothetical temporal data sets on deforestation after interpolation at a time slice of 1 min, due to the possibility of (a) acceleration, (b) delay, (c) overestimation, and (d) underestimation of deforestation detection, compared to the reference. Green crosses indicate overall similarity (i.e., the average of θ and δ similarities) from all nine metrics. Red lines on the upper edge of the envelopes indicate the overall similarity using the Fidelity metric. Blue lines on the lower edge of the envelopes indicate the overall similarity using the metric of Soergel–Ruzicka–Tanimoto.
Figure 25.
Overall similarity (i.e., the average of θ and δ similarities) of the temporal pattern between deforestation hotspots in Indonesia in 2020 derived from Landsat-8 OLI (at clarity ≥50% and deforestation intensity ≥50%) and deforestation hotspots in Indonesia in 2020 derived from MODIS (at change-detection thresholds ranging from 50 to 130), after interpolation at a time slice of 1 day. Green crosses indicate overall similarity (i.e., the average of θ and δ similarities) from all nine metrics. Red lines on the upper edge of the envelopes indicate the overall similarity using the Fidelity metric. Blue lines on the lower edge of the envelopes indicate the overall similarity using the metric of Soergel–Ruzicka–Tanimoto.
Figure 25.
Overall similarity (i.e., the average of θ and δ similarities) of the temporal pattern between deforestation hotspots in Indonesia in 2020 derived from Landsat-8 OLI (at clarity ≥50% and deforestation intensity ≥50%) and deforestation hotspots in Indonesia in 2020 derived from MODIS (at change-detection thresholds ranging from 50 to 130), after interpolation at a time slice of 1 day. Green crosses indicate overall similarity (i.e., the average of θ and δ similarities) from all nine metrics. Red lines on the upper edge of the envelopes indicate the overall similarity using the Fidelity metric. Blue lines on the lower edge of the envelopes indicate the overall similarity using the metric of Soergel–Ruzicka–Tanimoto.
Figure 26.
Overall similarity (i.e., the average of θ and δ similarities) of spatial pattern (red line) and temporal pattern (blue line) between deforestation hotspots in Indonesia in 2020 derived from Landsat-8 OLI (using the classification method described in
Appendix A, at clarity ≥50% and deforestation intensity ≥50%) and deforestation hotspots in Indonesia in 2020 derived from MODIS (using the change-detection algorithm developed by [
30], at change-detection thresholds ranging from 50 to 130). In this case, the overall similarity was calculated using the new Ruzicka–Fidelity metric (see Equation (1)), and time-series data were interpolated at a time slice of 1 day.
Figure 26.
Overall similarity (i.e., the average of θ and δ similarities) of spatial pattern (red line) and temporal pattern (blue line) between deforestation hotspots in Indonesia in 2020 derived from Landsat-8 OLI (using the classification method described in
Appendix A, at clarity ≥50% and deforestation intensity ≥50%) and deforestation hotspots in Indonesia in 2020 derived from MODIS (using the change-detection algorithm developed by [
30], at change-detection thresholds ranging from 50 to 130). In this case, the overall similarity was calculated using the new Ruzicka–Fidelity metric (see Equation (1)), and time-series data were interpolated at a time slice of 1 day.
Table 1.
Equations of nine similarity measures (S) between PDF pairs,
p and
q, with
n ordinal classes. We selected these nine PDF similarity measures out of the 45 metrics reviewed by [
29], as their values ranged from 0 (for a pair of very contrasting PDFs) to 1 (for a pair of exactly matching PDFs); the other metrics reviewed by [
29] resulted in similarity values ranging beyond sensible scales (e.g., the metrics of City Blok L1, Czekanowski, and Squared-Chord metrics had values ranging from −1 to 1).
Table 1.
Equations of nine similarity measures (S) between PDF pairs,
p and
q, with
n ordinal classes. We selected these nine PDF similarity measures out of the 45 metrics reviewed by [
29], as their values ranged from 0 (for a pair of very contrasting PDFs) to 1 (for a pair of exactly matching PDFs); the other metrics reviewed by [
29] resulted in similarity values ranging beyond sensible scales (e.g., the metrics of City Blok L1, Czekanowski, and Squared-Chord metrics had values ranging from −1 to 1).
| Metric | Equation |
|---|
| S∅rensen | |
| Soergel | |
| Intersection | |
| Ruzicka | |
| Tanimoto | |
| Cosine | |
| Jaccard | |
| Dice | |
| Fidelity | |
Table 2.
Spatial pattern similarity between two pairs of hypothetical patterns (shown in
Figure 5), measured using nine metrics (as listed in
Table 1), in terms of the geometric features used in this study (i.e., angle, θ, and distance, δ, from the centroid of the extent to each point). The overall similarity was calculated as the average of similarity of θ and similarity of δ.
Table 2.
Spatial pattern similarity between two pairs of hypothetical patterns (shown in
Figure 5), measured using nine metrics (as listed in
Table 1), in terms of the geometric features used in this study (i.e., angle, θ, and distance, δ, from the centroid of the extent to each point). The overall similarity was calculated as the average of similarity of θ and similarity of δ.
| Metric | Pair of Eagle Patterns | Pair of Turtle Patterns |
|---|
| θ | δ | Overall | θ | δ | Overall |
|---|
| S∅rensen | 0.48 | 1.00 | 0.74 | 0.98 | 0.39 | 0.68 |
| Soergel | 0.31 | 1.00 | 0.66 | 0.95 | 0.24 | 0.60 |
| Intersection | 0.48 | 1.00 | 0.74 | 0.98 | 0.39 | 0.68 |
| Ruzicka | 0.31 | 1.00 | 0.66 | 0.95 | 0.24 | 0.60 |
| Tanimoto | 0.31 | 1.00 | 0.66 | 0.95 | 0.24 | 0.60 |
| Cosine | 0.53 | 1.00 | 0.77 | 1.00 | 0.53 | 0.76 |
| Jaccard | 0.36 | 1.00 | 0.68 | 1.00 | 0.33 | 0.66 |
| Dice | 0.53 | 1.00 | 0.77 | 1.00 | 0.50 | 0.75 |
| Fidelity | 0.53 | 1.00 | 0.76 | 1.00 | 0.67 | 0.83 |
Table 3.
Overall similarity (i.e., the average of θ and δ similarities) using nine metrics of spatial pattern between deforestation hotspots in Indonesia in 2020, derived from Landsat-8 OLI (at clarity ≥50% and deforestation intensity ≥50%) and deforestation hotspots in Indonesia in 2020 derived from MODIS (at change-detection thresholds ranging from 50 to 130).
Table 3.
Overall similarity (i.e., the average of θ and δ similarities) using nine metrics of spatial pattern between deforestation hotspots in Indonesia in 2020, derived from Landsat-8 OLI (at clarity ≥50% and deforestation intensity ≥50%) and deforestation hotspots in Indonesia in 2020 derived from MODIS (at change-detection thresholds ranging from 50 to 130).
| Metric | MODIS Change-Detection Threshold |
|---|
| ≥50 | ≥60 | ≥70 | ≥80 | ≥90 | ≥100 | ≥130 |
|---|
| S∅rensen | 0.9444 | 0.9530 | 0.9607 | 0.9620 | 0.9600 | 0.9518 | 0.8920 |
| Soergel | 0.8950 | 0.9104 | 0.9246 | 0.9268 | 0.9232 | 0.9083 | 0.8054 |
| Intersection | 0.9444 | 0.9530 | 0.9607 | 0.9620 | 0.9600 | 0.9518 | 0.8920 |
| Ruzicka | 0.8950 | 0.9104 | 0.9246 | 0.9268 | 0.9232 | 0.9083 | 0.8054 |
| Tanimoto | 0.8950 | 0.9104 | 0.9246 | 0.9268 | 0.9232 | 0.9083 | 0.8054 |
| Cosine | 0.9960 | 0.9970 | 0.9977 | 0.9978 | 0.9975 | 0.9964 | 0.9765 |
| Jaccard | 0.9904 | 0.9934 | 0.9953 | 0.9957 | 0.9947 | 0.9920 | 0.9474 |
| Dice | 0.9952 | 0.9967 | 0.9977 | 0.9978 | 0.9974 | 0.9960 | 0.9729 |
| Fidelity | 0.9942 | 0.9960 | 0.9971 | 0.9974 | 0.9971 | 0.9963 | 0.9866 |
Table 4.
Overall similarity (i.e., the average of similarity of θ and similarity of δ) using nine metrics of temporal pattern between deforestation hotspots in Indonesia in 2020, derived from Landsat-8 OLI at clarity ≥50% and deforestation intensity ≥50%, and deforestation hotspots in Indonesia in 2020, derived from MODIS at change-detection thresholds ranging from 50 to 130.
Table 4.
Overall similarity (i.e., the average of similarity of θ and similarity of δ) using nine metrics of temporal pattern between deforestation hotspots in Indonesia in 2020, derived from Landsat-8 OLI at clarity ≥50% and deforestation intensity ≥50%, and deforestation hotspots in Indonesia in 2020, derived from MODIS at change-detection thresholds ranging from 50 to 130.
| Metric | MODIS Change-Detection Threshold |
|---|
| ≥50 | ≥60 | ≥70 | ≥80 | ≥90 | ≥100 | ≥130 |
|---|
| S∅rensen | 0.4130 | 0.3913 | 0.4783 | 0.3696 | 0.4783 | 0.5435 | 0.6522 |
| Soergel | 0.2797 | 0.2664 | 0.3417 | 0.2446 | 0.3690 | 0.4456 | 0.5416 |
| Intersection | 0.4130 | 0.3913 | 0.4783 | 0.3696 | 0.4783 | 0.5435 | 0.6522 |
| Ruzicka | 0.2797 | 0.2664 | 0.3417 | 0.2446 | 0.3690 | 0.4456 | 0.5416 |
| Tanimoto | 0.2797 | 0.2664 | 0.3417 | 0.2446 | 0.3690 | 0.4456 | 0.5416 |
| Cosine | 0.5327 | 0.5127 | 0.5653 | 0.4792 | 0.5841 | 0.6124 | 0.6968 |
| Jaccard | 0.3896 | 0.3787 | 0.4349 | 0.3395 | 0.5059 | 0.5491 | 0.6151 |
| Dice | 0.5005 | 0.4769 | 0.5365 | 0.4464 | 0.5675 | 0.6072 | 0.6950 |
| Fidelity | 0.5055 | 0.4767 | 0.5454 | 0.4956 | 0.5500 | 0.5998 | 0.7107 |
Table 5.
Sensitivity summary of the method on hypothetical temporal data sets on deforestation after interpolation at a time slice of 16 days, 1 day, 1 h, and 1 min, due to the possibility of (a) acceleration, (b) delay, (c) overestimation, and (d) underestimation of deforestation detection, compared to the reference.
Table 5.
Sensitivity summary of the method on hypothetical temporal data sets on deforestation after interpolation at a time slice of 16 days, 1 day, 1 h, and 1 min, due to the possibility of (a) acceleration, (b) delay, (c) overestimation, and (d) underestimation of deforestation detection, compared to the reference.
| Time Interval | Equidistance Interpolation Slice from the Original time Interval | Linear Slope, Indicating Sensitivity Due to |
|---|
| Acceleration, from 16 to 80 Days from the Reference | Delay, from 16 to 80 Days from the Reference | Overestimation, 1 Pixel to 5 Pixels from the Reference | Underestimation, 1 Pixel to 5 Pixels from the Reference |
|---|
| 16-day | 1× | −0.0026 | −0.0027 | −0.0526 | −0.0379 |
| Daily | 16× | −0.0026 | −0.0045 | −0.0230 | −0.0214 |
| Hourly | 384× | −0.0026 | −0.0027 | −0.0034 | −0.0033 |
| Minutely | 34560× | 0.0001 | 0.0000 | 0.0000 | 0.0000 |