Toward Cancer Chemoprevention: Mathematical Modeling of Chemically Induced Carcinogenesis and Chemoprevention ^†

Abstract

Cancer, which is currently rated as the second-leading cause of mortality across the globe, is one of the most hazardous disease groups that has plagued humanity for centuries. The experiments presented here span over two decades and were conducted on a specific species of mice, aiming to neutralize a highly carcinogenic agent by altering its chemical structure when combined with certain compounds. A plethora of growth models, each of which makes use of distinctive qualities, are utilized in the investigation and explanation of the phenomena of chemically induced oncogenesis and prevention. The analysis ultimately results in the formalization of the process of locating the growth model that provides the best descriptive power based on predefined criteria. This is accomplished through a methodological workflow that adopts a computational pipeline based on the Levenberg–Marquardt algorithm with pioneering and conventional metrics as well as a ruleset. The developed process simplifies the investigated phenomena as the parameter space of growth models is reduced. The predictability is proven strong in the near future (i.e., a 0.61% difference between the predicted and actual values). The parameters differentiate between active compounds (i.e., classification results reach up to 96% in sensitivity and other performance metrics). The distribution of parameter contribution complements the findings that the logistic growth model is the most appropriate (i.e., 44.47%). In addition, the dosage of chemicals is increased by a factor of two for the next round of trials, which exposes parallel behavior between the two dosages. As a consequence, the study reveals important information on chemoprevention and the cycles of cancer proliferation. If developed further, it might lead to the development of nutritional supplements that completely inhibit the expansion of cancerous tumors. The methodology provided can be used to describe other phenomena that progress over time and it has the power to estimate future results.

1. Introduction

Cancer is one of the most dangerous disease groups currently affecting developed nations, highlighted as the second-leading cause of death worldwide, after heart conditions [1]. Statistics indicate that the most common cancer types in terms of new cases are breast, lung, colon and rectum, prostate, skin, and stomach. In terms of mortality, lung, colon and rectum, liver, stomach, and breast cancer are the most prevalent [2]. A third of cancer mortality is attributed to modifiable behaviors, such as using tobacco products, drinking alcohol, consuming foods with poor nutritional value, and not exercising [3,4]. Nevertheless, regardless of the type of neoplasm, cancer can be effectively treated if diagnosed early. Minimizing the risk factors mentioned above may also significantly lower the likelihood of tumor development [5].

Cancer develops when normal cells undergo a multi-stage process that often progresses from a precancerous to a malignant state, resulting in tumor cells [6]. Technological advances have significantly contributed to cancer treatment by introducing immunotherapies capable of targeting genetic and protein abnormalities in cancer cells. This is particularly valuable when patients have exhausted options after other therapies have failed [7,8]. Recent years have also seen a focus on targeted treatments as well as the states and features of metastatic cells [9,10]. Despite intense scientific interest, little progress has been made in terms of chemoprevention. As chemoprevention has been explored for treating various malignancies, interest in understanding oncogenesis and identifying potential molecular targets to impede the process has magnified. The developed approach focuses on the use of organic, inorganic, or biologically active substances to delay, stop, or reverse the progression of tumors. Several techniques, including the activation of free radical scavenging enzymes and the management of chronic inflammation, can potentially stop the uncontrollable growth of tumors [11].

This study expands on prior research [12] by mathematically elucidating the phenomenon of chemical oncogenesis induced in a specific mouse species through the surgical administration of the carcinogenic agent 3,4-benzopyrene (BP). Additionally, it investigates the concept of chemical prevention by combining compounds from the polyamine (PA) or thiol (TH) families with BP. The analysis involves employing various mathematical functions to realistically depict and forecast these phenomena, emphasizing curve fitting and evaluating model performance. The study introduces a methodological workflow for selecting the most descriptive growth model, incorporating a graphical approach and innovative metrics for assessing model performance over time. This research diverges from the previous one by exposing experimental subjects to double dosages, enhancing the depth of investigation. It provides a comprehensive literature review on oncogenesis, contributing to contextual understanding. The inclusion of diverse growth models adds methodological sophistication and detailed experimental procedures enrich the scientific methodology. This study also explores clinical implications, emphasizing the potential translational impact within clinical practice.

The contribution of this work is not limited to modeling phenomena and accurately predicting their progression over time using progression metrics and illustrations. It further expands to formalizing a methodological workflow that can be adopted in a variety of fields utilizing time-related data. The proposed workflow considers a predefined ruleset that can be adapted to the respective needs, numerous growth models, a computational curve fitting pipeline capable of dealing with the initial guess problem, the performance of the models based on a series of key performance and progression indicators, and the interpretation of the resulting information; this approach aims to provide valuable insights for the explanation, predictability, and overall simplification of the corresponding events.

2. Growth Models

Due to their similarity to homeostasis, the mechanism through which individuals maintain optimal functioning conditions, sigmoid functions are anticipated to yield better results. Therefore, various functions, including exponential, Gompertz, Bertalanffy, logistic, Gauss, third-degree polynomial, Brody, Weibull, and power law, were employed to explore their capacity to capture tumor size development.

The exponential function was leveraged to capture cases where the homeostasis mechanism declined, resulting in rapid multiplication of the tumor. The exponential function assumes a constant ratio between the growth rate of cancer cells and the total number of cancer cells at a given time. It is denoted as

$$V=V_0{e}^{\lambda t}.$$

(1)

The constant ratio is denoted by $\lambda$, which is an arbitrary constant. Similar to e and $\lambda$, it is easy to notice that the doubling time of the quantity V is constant, as $V_0$ reflects the initial weight of the tumor and does not vary.

The Gompertz model, originally conceptualized in 1825 by Benjamin Gompertz, was developed to describe the mortality rates of human populations. Despite its historical origins, this mathematical model continues to find relevance and utility in contemporary scientific and epidemiological studies. One prominent example of its ongoing application is in the context of simulating and analyzing the spread of infectious diseases such as COVID-19 [13]. Schematically, this model initially resembles the exponential model; however, there are no substantial changes in the time domain near the conclusion of the curve. The mathematical expression is given as follows:

$$V=V_0{e}^{a(1-e^{-bt})},$$

(2)

where $V_0$ represents the initial weight of the cancer, a represents the x-axis displacement, and b represents the growth rate. Gompertz is a sigmoidal curve that is mostly employed for advanced-stage tumors because it is manifestly unsuitable for smaller tumors. When the tumor proliferation rate approaches infinity in sufficiently tiny tumor volumes, the model does not provide a realistic depiction. Specifically, any growth equation or model that follows a relative growth rate of the type P/Q, with P tending to infinity as Q goes to zero, cannot explain or reflect the complicated biological events that occur during the cell cycle and apoptosis. The latter processes rely on doubling times, which cannot accept arbitrarily small values.

The Bertalanffy function was originally devised—and is currently employed—to model the population increase of fish and other animals [14,15], but it has also proven to be an effective model for describing the development of cancer cells. This model’s distinctive feature is that it is based on the theory of metabolism, which can be proven experimentally. The following are hypotheses that were relied on. The growth rate reflects the difference between the anabolic and catabolic rates and the ratio between cell death and cancer cell death. In addition, the disease’s morphology does not alter despite the fact that the anabolic rate is related to the cancer cells and the volume is proportional to the surface area. Consequently, the formula of the function is as follows:

$$\frac{dV}{dt}=n{V}^{2/3}-mV\Rightarrow V=b_1{(1-b_2^{e^{-b_{3}t}})}^3,$$

(3)

where n and m are analogy-indicating parameters. Geometrically, this model approximates the logarithmic function, which is the inverse of the exponential function. It is concave in shape and the kurtosis suggests that this model will fit well in the second and third phases of cellular cancer growth, as it has both a linear component at the beginning and a smoothing of values at the conclusion.

The Verhulst–Pearl model, also known as the logistic equation, was developed in 1845 to describe the increase in population. This concept is quite close to Bertalanffy’s but more adaptable. If early-stage observations reveal behavior comparable to exponential development, we select a small value for ‘b’. In this instance, the logistic model shares behavior with the exponential model across the whole time domain. If the data do not exhibit exponential behavior, we select a large ‘b’ to achieve the desired slowdown in cancer cell development. Its original purpose was to depict the self-limiting growth of a biological population, based on the idea that the reproduction rate is proportional to both the existing population and the amount of available resources. From the shape of this sigmoid function, additional information can be derived. Parameter ‘a’ sets the growth rate, whereas ‘b’ provides the maximal mass of cancer cells, as shown in

$$\frac{dV}{dt}=\alpha V-\beta V^2\Rightarrow V=\frac{\alpha }{e^{-\alpha t}\frac{a}{V_0-b}+b}.$$

(4)

Thus, the line $y=\frac{a}{b}$ is an asymptote of the logistic function on the horizontal axis. In biology, organisms are classified as a-strategic or $\frac{a}{b}$-strategic based on the natural selection during their historical evolution. Consequently, these parameters influence the evolution and inheritance of species. In the current scientific landscape, it is notable that a substantial number of researchers have adopted the logistic model as a valuable tool for forecasting cumulative cases of infectious diseases, such as COVID-19, and for modeling the dynamics of insect outbreaks [16,17]. This mathematical model, originally introduced by Pierre François Verhulst and widely applied in epidemiology and population ecology, continues to be a favored choice for addressing these crucial scientific challenges.

The Gaussian function is a statistics-based model characterized by a symmetric curve with a bell-shaped shape, denoted as

$$V=a{e}^{\frac{-{(x-b)}^2}{2c^2}}.$$

(5)

Parameter ‘a’ represents the curve’s height. Argument ‘b’ specifies the location of the bell’s center, while parameter ‘c’ specifies its width. A bell-shaped morphology is attributed to sigmoidal phenomena because its components can be isolated. Keeping the beginning of the curve and its largest height constant, the curve follows a conventional sigmoidal shape. Therefore, exponentiality, linearity, and convexity are all satisfied. Due to the symmetry of the curve, the third component (convexity) is restricted in time, as it is followed by a sharp decrease in the curve and hence appears diminished in size. As aging contributes to a more gradual and symmetric process, this model has not been applied to cancer cell growth, whereas it has been extensively applied to the description of plant growth.

The polynomial model is widely employed in general growth modeling and is an empirical model without a strong physiological basis. Studies typically employ polynomial models, models derived from divisions of these (e.g., explicit models), and other operations, such as the addition of two polynomials with different parameters (e.g., the two-term polynomial model). The key benefits of these models stem from their simplicity, interpretability, adaptability, and ease of application. However, there are several drawbacks to this model. Models with a high degree of polynomial degree generate oscillations between values of high precision. Polynomials are capable of adapting to a variety of data types, but their oscillatory nature typically allows them to escape the boundaries. In addition, by their very nature, polynomials have a limited understanding of asymptotic behavior and, hence, may not accurately model asymptotic phenomena. In conclusion, polynomials exhibit a particularly poor trade-off between morphology and degree. Third- and fourth-degree polynomials are the most commonly used since a higher degree reduces the bias and results in overfitted data. In the current study, third-degree polynomials were used; their formula is as follows:

$$V=p_{1}t+p_2{t}^2+p_3{t}^3+p_4.$$

(6)

The Brody growth model for biological growth was developed in 1945. While its descriptive ability has been applied to breast cancer cell growth with an interest in the breast region, the model has not been sufficiently applied to malignant growth using actual data [18]. Thus, we cannot be certain of the conclusions obtained beforehand. However, the slope of this model is initially logarithmic and smooths out over time. We utilize the following formula:

$$V=A(1-B{e}^{-kt}),$$

(7)

where A is the upper asymptote of the curve and serves as the upper limit for the function. Theoretically, it should fail to reproduce the first recordings of the experiments, but it will more closely resemble the time-averaged recordings of longer durations.

The Weibull distribution in probability theory and statistics is a continuous probability distribution. It is named after Wallodi Weibull, a Danish mathematician who described it in detail in 1951. As a mathematical model and, consequently, a growth model, it is extremely adaptable, as its morphology can alter significantly. It is capable of both symmetric sigmoidal and logarithmic forms. The formula for the three-parameter Weibull model is as follows:

$$V=A(1-e^{-k{t}^m}),$$

(8)

where A marks the upper asymptote of the curve and serves as the upper constraint for the cancer mass, whereas k is a morphological factor similar to m. Also, the Weibull and Brody models have a close relationship, as in the case where ‘m’ and ‘B’ are equal to 1, the models are identical. The Weibull model has been a significant and enduring analytical tool in the realm of oncology for several decades. Currently, its versatile application includes estimating cancer latency times [19] and analyzing gastric cancer patient survival [20], exemplifying its utility in both research and clinical settings.

The power law model assumes that a relative change in one quantity results in a proportional change in another, independent of their original sizes. Specifically, one quantity is identified as the driving factor of the other. The mathematical formula for this function is

$$V=A{t}^{-b}.$$

(9)

Considering the model to be a straight proportional function, it performs well on data with a small number of records that mostly capture the exponential phase, but not as effectively on data with a larger number of records. However, we would like to emphasize its natural basis, which is the existence of a ratio between time and cancer weight. As the ratio of quantities varies during each phase of homeostasis, it would likely be more appropriate to apply three distinct power law functions. However, due to the uniqueness of organisms and their responses, we do not know the exact or even approximate time frames of when these changes occur.

In order to present the most realistic explanation of oncogenesis and inhibitory mechanisms, it is necessary to identify some criteria that growth models must satisfy in order to end this discussion. Therefore, we desire the model to adequately approximate multiple data series, reflect comparable behavior, and avoid oscillations between ideal and subpar outcomes. These criteria need to be translated into mathematical expressions and integrated into the developed framework, as shown in

Table 1. Growth model criteria and their implementation.

Criteria	Method
Adequately approximate multiple data series	On the basis of the high-performance indicators (e.g., SSE), the model should capture a large proportion of data series (e.g., 80%)
Reflect comparable behavior	Avoid models whose behaviors are inconsistent across data.
Avoid oscillations between ideal and subpar outcomes	Avoid models whose performance values are the lowest for some data and the highest for others.

. However, it is important to note that these criteria are quite stringent and it is possible that no existing model may meet all of them. Therefore, it may be necessary to relax some of the constraints to ensure that the framework remains feasible.

3. Related Work

The role of chemopreventive natural substances has been extensively studied in the literature, but few clinical trials have been conducted to validate and demonstrate their efficacy. For instance, the chemopreventive capabilities of phytochemicals produced from diverse medicinal plants have been shown to reduce several risk factors linked to different types of cancer [21]. The significance of antioxidants in chemoprevention, carcinogenesis, and chemoprevention processes utilizing this strategy were further elaborated, showing that curcumin [22], resveratrol [23], hesperidin [24], quercetin [25,26], and gingerol [27], among others, can potentially regulate certain genes to inhibit tumor invasiveness, anti-migration, antiproliferation, and apoptosis. It is also worth noting that, on certain occasions, compounds of organic origin derived from venomous organisms, flora, or microorganisms provide a more elucidating perspective on the molecular compositions and mechanisms of action underpinning their efficacy in combating cancer [28], such as Cuban Blue Scorpion’s venom [29] and paclitaxel derived from the bark of the Pacific yew tree (i.e., Taxus brevifolia) [30].

Broadly, dietary polyphenols display chemopreventive effects by modulating apoptosis, autophagy, cell cycle progression, inflammation, invasion, and metastasis [31]. Polyphenols have potent antioxidant properties and regulate various molecular events by activating tumor suppressor genes and inhibiting oncogenes implicated in carcinogenesis. Polyphenols can be considered as a potential cancer medication as well, presenting both advantages and disadvantages [32]. Their ability to target cancer cells in various ways is a key benefit, preserving host cell integrity. However, their limited bioavailability poses a challenge, requiring high doses that may be harmful. This drawback can be mitigated through a plant-based diet. Studies show a growing preference for plant-based or alternative treatments among cancer patients, emphasizing the need to enhance treatment efficacy and reduce side effects [33].

In the context of practical application, the development of tumor growth models under bevacizumab treatment in a mouse population has also been conducted [34]. The model incorporates equations for tumor cell proliferation, inhibitor clearance, and the drug’s inhibitory effect on tumor growth. Notably, it simplifies the drug’s indirect impact on angiogenesis, a factor influencing tumor growth. The resulting differential equations, derived from mass-action kinetics, describe measurable tumor volume, with model parameters including the tumor growth rate, inhibition rate, and inhibitor clearance, identified from experiments.

Investigations into discrete mathematical models for the study of aggressive and invasive cancers have been pursued, deviating from conventional growth models [35]. These models account for cancer heterogeneity, mutation rates, tumor microenvironment acidity, cellular competition, resistance to chemotherapy, and drug toxicity. By considering these factors, the research provides a more comprehensive and dynamic approach to understanding cancer dynamics and identifying effective treatment strategies. The proposed approach was validated through simulations involving various parameter sets. Adhering to a coherent approach to discrete modeling, a novel approach to modeling pharmacokinetics–pharmacodynamics for tumor growth and anticancer effects in a continuous time framework has also been devised [36]. The emphasis is on a daily time scale, using data derived from NMRI female mice experimentation. The innovation lies in transforming this continuous model into a discrete system of nabla fractional difference equations using Riemann–Liouville fractional derivatives. In parallel, an online tool for the statistical analysis of tumor growth curves over time has been developed [37]. These curves are developed based on the tumor’s diameter, surface area, and volume. The proposed software tool provides a series of statistical tests that can be performed across and between different groups of tumor growth. Additionally, it generates a diverse arsenal of visualization and analytical tools that can be applied to complex datasets, including longitudinal, cross-sectional, and time-to-endpoint measurements.

The performance of growth models against their fractional variations has also been tested, revealing the superiority of the former over their integer-order counterparts [38]. This conclusion emerges naturally when an additional parameter is added to the models, increasing complexity while also enhancing curve flexibility. The exponential models showed the highest performance for the experimental breast cancer data, highlighting the necessity of adopting higher-order fractional growth models to improve their ability to forecast the future. To assess the applicability of logistic, exponential, and Gompertz models, a comprehensive analysis was conducted on experimental data from three distinct animal models with breast and lung cancer [39]. The Gompertz model performed significantly better than the others, with its parameters showing a significant correlation. By exploiting this correlation, the dimensionality of the model was reduced, which led to the creation of a more simple function. When Bayesian inference was used in conjunction with the previous function to estimate the times of tumor incidence, it was shown that it was highly efficient.

4. Materials and Protocols

The data presented herein, although limited in volume, robustly demonstrate a strong proof-of-concept for the developed theoretical and methodological approaches. Despite its limitations, this dataset is sufficient to unveil meaningful insights and achieve statistical significance. These findings substantiate the validity and efficacy of our approach within the confines of the study’s design and available resources, especially considering the sensitivity to experiments on animals. Moreover, we have thoughtfully considered and justified the choices, balancing the need for scientific rigor with ethical, legal, and regulatory concerns. It is worth noting that addressing this limitation through future research has the potential to yield narrower confidence intervals, consequently enhancing the reliability and informativeness of the results. However, it is important to emphasize that such an endeavor lies beyond the scope of the present article.

4.1. Naval Medical Research Institute Mice

The inclusion of Naval Medical Research Institute (NMRI) mice in the study was based on several considerations, the most pivotal being the anatomical analogy in the body and organ sizes. Notably, the female NMRI mice, with a weight range of 40–50 g, contrast sharply with the average human body weight of 70 kg, representing a size differential of approximately 1550 times. This analogy is further emphasized by the congruence in organs and tissues of mice and humans, regardless of their size and morphology.

Furthermore, the proportional variations in size across organs and muscles between mice and humans enhance the translational significance of the research outcomes. This enhancement facilitates a more seamless extrapolation of potential findings from the study to the human context. This strategic alignment underscores the paramount importance of considering anatomical similarities to extrapolate insights that may have implications for human health. It is also imperative to note that their physiological processes adhere to the same rules, maintaining consistent ratios across species. This parallelism in physiological mechanisms further reinforces the reliability and applicability of the study’s outcomes to the understanding of human biological processes, although these two species generally diverge in the following ways:

a.

The greater functional rhythms of the mouse (e.g., tachycardia and tachypnea animal), which relate to all of its functions. These heightened rhythms are probably also connected to the limited lifespan of these tiny rodents.

b.

Animals kept in captivity have a longer lifespan of between one and two years, whereas the wild type’s lifespan (i.e., survival expectancy) is approximately 12 months.

c.

The movements and neural conductivities in mice are notably swifter than those observed in humans.

d.

Mouse pregnancies exhibit a higher degree of polyembryony (e.g., >4–8 embryos per gestation) in contrast to the infrequent occurrence of polyembryony in humans.

4.2. Experimental Protocol

To acquire the dataset, the single-dose experiment involved 289 NMRI mice, while the double-dose experiment involved an additional 150 subjects. The exclusive use of female NMRI mice in this study is a strategic decision informed by their smaller body sizes and weights. This deliberate selection aims to enhance experimental precision by minimizing variations in chemical dosage requirements, thereby fostering a controlled and standardized research environment. These smaller sizes will also assist in their better handling, while the inherent reproductive characteristics, such as the polyovular nature of female mice, might contribute to the understanding of hormonal influences on cancer development, potentially enriching the evaluation of the impact of chemical carcinogens within the context of this study. The trials adhere to the established protocol outlined in the work by Kallistratos et al., which focuses on the inhibition of cancerogenesis using vitamin C on Wistar rats [40].

The Experimental Animal Husbandry provided four pairs of NMRI mice, housed in the dedicated Laboratory of Experimental Physiology breeding facility for small animals under controlled conditions. The entire NMRI mouse population for the study originated from these pairs through inbred crossings, resulting in a genetically uniform population with consistent traits, which facilitated standardized responses to the chemical carcinogen’s metabolism.

The injection of the carcinogenic agent, which was carried out surgically under anesthesia induced by a single intraperitoneal administration of sedative (3 milligrams of midazolam per kilogram of body weight) and anesthetic (3 milligrams of ketamine per kilogram of body weight), occurred sixty days after their birth. Iodine and hydrogen peroxide were used for local disinfection after anesthesia. A small incision was made in the skin to expose the underlying muscle mass of the right shoulder. Consequently, a fixed amount (2.52 mg/mL) of BP dissolved in tricaprylin was then injected under the muscular peritoneum. To stop the carcinogenic fluid from leaking out of the animal’s body, the wound was promptly sutured and carefully closed. The same protocol was adhered to for the mice subjected to the combined administration of BP with PA or TH, with PA or TH being co-administered with BP only once for the duration of the study.

Experimental animals were monitored three times daily (i.e., 8:00 AM, 4:00 PM, and 8:00 PM) following carcinogen administration. General anesthesia was administered at intervals for ultrasonic tomography scans in the scapula region to assess tumor size and conversion to weight units (mg). Anesthesia played a crucial role in ensuring accuracy, reliability, and ethical treatment by immobilizing the mice, preventing movement-induced distortions, reducing stress and injury risk, along with enhancing safety. It facilitated precise positioning, improved data accuracy, minimized artifacts, and aligned with ethical standards for humane animal research.

A cage change occurred when the tumor size significantly increased, and the subject’s health deteriorated. Weighing and necropsy were performed post-mortem, with internal organs examined, weighed, and photographed after tumor removal. For histopathological analysis, the tumor and organs were submerged in an 8% formaldehyde solution, wrapped in absorbent paper, and prepared for microscopic examination. A pathologist diagnosed, examined, and recorded any metastases. The carcass review and sections were fixed to contrast the neoplastic disease’s intensity and extent. Pathological anatomical analysis, including tumor characteristics and biological findings, was crucial in evaluating anticancer agent effectiveness. The study considered factors such as malignant tumor development, original tumor size, growth rate, and the correlation between carcinogen and anti-carcinogen weights to determine inhibition levels.

4.3. Theoretical Approach toward Neutralization

BP is a chemical substance that is produced when some chemicals are not entirely burnt [41]. It can be detected in food that has been grilled, car exhaust, wood smoke, tobacco, and oil, among other sources. It belongs to the category of polycyclic aromatic hydrocarbons, also known as 3,4-benzopyrene [42]. The experimental approach of chemical carcinogenesis in NMRI mice via BP was largely chemical. Specifically, we aimed to neutralize or alter the chemical structure of BP by incubating a quantity of it with specific amounts of various substances, which could potentially react together, particularly making addition reactions to its double bonds. The theoretical background suggested that these reactions could weaken the double bonds, especially those in the ‘L’ and ‘K’ regions, allowing BP to take on a chemical structure analogous to that of chrysene, which is also a polycyclic aromatic hydrocarbon but is substantially less carcinogenic than BP [43]. The basic idea behind these experiments was to assess the validity of the theory that modifying specific structural points of polycyclic aromatic hydrocarbons could eliminate their carcinogenic potential. Chemical oncogenesis, induced by 2.52 mg of BP, resulted in tumors appearing in experimental animals within 60 days, with some developing malignant tumors in just 20 days. The tumors progressed rapidly, leading to mortality upon reaching a critical size. All but two animals succumbed between 120 and 190 days after birth, forming a dataset with tumor mass estimates and examination dates. Subsequent sections will detail drug combinations involving benzopyrene with PA or TH.

4.4. Polyamines and Thiols

The amino acids L-arginine and L-ornithine normally break down into compounds known as PAs, which protect deoxyribonucleic acid (DNA). Specifically, they are substances from the microcosm essential for the development of eukaryotes. They are able to bind to anionic macromolecules like ribonucleic acid (RNA), DNA, proteins, and phospholipids due to their flexibility and charge distribution. The contribution of PAs to physiological cellular functions is further highlighted by their roles in chromatin structure maintenance, ion channel regulation, membrane stability preservation, and free radical removal [44].

Under physiological circumstances, a complex network of biosynthetic, catabolic, and unexplained transport (i.e., not all transport parameters are known) systems carefully controls the PA levels. Although the amount of free PAs is significantly lower in reality, these regulations serve to maintain a concentration of PA in the cell. It has been demonstrated that an increase in the polyamine concentration inside cells is associated with an increase in cell proliferation and, as a result, the development of tumors. Several works from the literature have explored the correlation between intracellular polyamine concentration and cancer progression in terms of functionality, metabolism, and overall immunity [45,46,47]. Therefore, the role of PA in chemopreventive and chemotherapeutic agents has been widely documented but not fully understood.

Ethylenediamine, cadaverine, and putrescine are three compounds from the PA family that were used in the experiments, whereas the same compounds were used in a second series of experiments with double the anti-carcinogenic dosages.

Table 2. Polyamine compound distribution: total experimental subjects and tumor observation across groups, dosages, and administered compounds.

Group	Dosage	Compound	Tumor Obs.	Total Obs.	Incidence (%)
Carcinogen	2.52 mL	Benzopyrene	49	49	100
Polyamines	Single	Ethylenediamine	2	19	10.52
		Cadaverine	12	30	40.00
		Putrescine	2	43	4.65
		Total	16	92	17.39
	Twofold	Ethylenediamine	1	50	2.00
		Cadaverine	5	50	10.00
		Putrescine	1	50	2.00
		Total	7	150	4.66
		Total	23	242	9.50

presents data on the efficacy of PAs concerning the occurrence of malignant tumors at both single and twofold concentrations, demonstrating a noteworthy reduction in incidence from 17.39% to 4.66%. The incidence of malignant tumors refers to the percentage of the population in which tumors were observed, as outlined in the table.

THs, which are present in amino acids, are also part of the microcosm. The most common thiol is cysteine, and its residues can be found in proteins and smaller molecules. Glutathione, a tripeptide containing cysteine, which is widely present in cells, is an example of such a molecule. L-cysteine serves as an example of the important distinction between TH and PA, which are designed to protect and fight against oncogenesis. The double bonds in benzopyrene are susceptible to addition reactions in the presence of the amino acid L-cysteine. When using the ethyl or methyl ester of L-cysteine as an anti-carcinogenic molecule, as opposed to L-cysteine alone, the addition of -SH to the double bonds of benzopyrene occurs in a much more quantitative manner, indicating that this phenomenon not only occurs but is also exacerbated by the formation of the ester bond in the carboxyl group of the cysteine amino acid.

By examining (with a mass spectrometer) the molecules resulting from the reaction of benzopyrene with commonly used chemicals in such investigations, the image will become significantly more distinct. The primary distinction between PA and TH is that the former acts as the organism’s shield by preserving DNA, RNA, proteins, and phospholipids, whereas TH serves as the organism’s sword by attempting to neutralize the carcinogenic agent. We also present the distribution of the TH family (

Table 3. Thiol compound distribution: total experimental subjects and tumor observation across groups, dosages, and administered compounds.

Group	Dosage	Compound	Tumor Obs.	Total Obs.	Incidence (%)
Carcinogen	2.52 mL	Benzopyrene	49	49	100
Thiols	Single	Bismuthiol	21	30	70.00
		L-Cysteine Ethyl Ester	7	28	25.00
		Mercaptosuccinic Acid	12	30	40.00
		Dithiothreitol	8	30	26.66
		L-Cysteine	11	30	36.66
		Total	59	148	39.86

), which inhibited oncogenesis to a lesser extent than PA. Consequently, no additional investigation, which could require a dose-escalation experiment, was carried out on this anticancer drug combination.

5. Methodology

5.1. Curve Fitting Computational Pipeline

Tumors can be viewed as populations, and their development can be anticipated using complex growth models. The modeling of any population growth is a least-squares problem that can be further classified as linear or non-linear depending on the leveraged function. In essence, least squares problems seek to design a curve that optimally fits a set of data points. In this work, the Levenberg–Marquardt algorithm (LMA) was applied because it shares characteristics with gradient descent and Gauss–Newton methods; moreover, the majority of the adopted models were non-linear. The sum of squares error (SSE) was used as the objective function for the curve fitting technique, while the root mean square error (RMSE) and mean absolute error (MAE) were applied as goodness-of-fit metrics.

In non-linear least squares problems, the initial guess is the most difficult part because there is no universal technique that works. However, for the family of growth modeling problems, viable solutions have been established. In the proposed methodology, the initial guess parameters were produced from the SPSS non-linear regression package in conjunction with estimations from prior scientific work [48] and from the use of three consecutive values to generate a 3 × 3 system of equations for the three-parameter models. In a similar manner, parameters of the four-parameter models were obtained. In instances where the algorithm did not converge, the final values from the converged solution were used and a broad range of starting points was utilized. Several additional simulations were performed with the given range to ensure that the algorithm did not converge on a local extremum, but rather on a global extremum.

5.2. Performance Evaluation

In addition to the goodness-of-fit and objective function values, model parameters were also obtained after LMA convergence. Using the coefficient of variation (CV), the reliability and central tendency of the derived parameters were further evaluated, respectively. The conducted analysis may result in model simplification by reducing the number of varying parameters, hence, facilitating reproducibility.

After the computational pipeline, each function has a unique SSE, RMSE, and MAE value per data series. The minimum value corresponds to the optimal function for that particular cancer cell development, as it demonstrates that the generated curve is the closest to the ground truth. However, if we relax the rigor of the criteria initially specified to allow a 5% deviation from the minimum value, other functions may exhibit favorable behavior. This results in the creation of %-tolerance metrics, which permit a specified percentage of value variation to be tolerated in the respective measurement. These analytical methods can also be used to depict and illustrate which of the models has the most descriptive power on the investigated phenomena under relaxed criteria, while allowing scientists to determine when to cease breaching the rules (e.g., using the elbow method).

5.3. Model Predictability and Classification Problem

To evaluate the growth models’ ability to forecast the future based on past knowledge, the data series were divided into two sets: the training set and the testing set. The first set was used to generate a curve using the previously described computational workflow, while the second set was used to calculate the mean percentage difference between the projected and the actual values. Only data series including at least fifteen examinations were included in this section of the study. It was assumed that the forecast would be limited since cancer grows exponentially after a certain point. However, even if this was not the case, some conclusions could still be drawn regarding the near-future predictions.

Using the model parameters, binary classification problems were developed to differentiate carcinogenic and anticarcinogenic agents in three settings:

a.

Benzopyrene against benzopyrene with both administered anticarcinogenic agents (BPAC);

b.

Benzopyrene against benzopyrene with polyamines (BPPA);

c.

Benzopyrene against benzopyrene with thiols (BPTH).

The classification problem exploits the parameter space to differentiate the two groups; thus, the variability of the parameters, which were disguised as features, plays a vital role. Grid search and cross-validation accuracy were used to perform parameter tuning. By employing the ReliefF method, the relevance of each feature was also determined, leading to the contribution of growth models to the classification task. K-nearest neighbors (KNNs) and support vector machines (SVMs) with a linear kernel were selected as the primary classifiers. Due to overfitting and the models’ inherent simplicity, more sophisticated kernels were omitted. Accuracy, sensitivity, and specificity were computed to evaluate the performance of the classifiers. Nevertheless, due to class imbalance, positive predictive value, g-mean, f2, and adjusted f2 measure were also calculated in addition.

5.4. Statistical Analysis

A statistical analysis was performed in order to examine the mortality of mice in greater detail and compare the efficacy of the chemical compounds. After the introduction of normality tests, distributions were compared instead of populations. These normality tests include Anderson–Darling, Jarque–Bera, Lilliefors, and Shapiro–Wilk tests, each of which emphasizes a distinct aspect of normal distribution. For nonparametric tests, the Kolmogorov–Smirnov and Mann–Whitney U tests were applied. In addition, statistical moments up to the fourth degree were employed to investigate central tendencies, variability, symmetry, and heaviness. Lastly, graphical representations were utilized, such as QQ plots, to illustrate the numerically driven insight.

5.5. Methodological Workflow Overview

The proposed workflow accepts numerical data series as input and delivers the growth model that possesses the highest descriptive power as output (Figure 1). It starts with the preparatory phase, moves on to the computational phase, then the performance evaluation phase, and finally the progression evaluation phase.

The ruleset and the growth models are both specified in the first phase of the workflow. The non-linear least squares algorithm and the initial guess issue are both explored and executed, respectively, during the computational phase. After the LMA algorithm has converged, the performance evaluation will take place; this will be followed by the progression evaluation, which occurs after certain halting conditions have been satisfied. The growth models that are used for this study are documented in Section 2, and the ruleset is established at the very end of the same Section. In Section 5.1, we discuss the non-linear least squares algorithm and the initial guess issue, while Section 5.2 is where we evaluate performance and progression.

6. Results

6.1. Growth Model Performance

The logistic function produced the lowest SSE, RMSE, and MAE values in all experiments encompassing about two-thirds of the mice population in BP. Specifically,

Table 4. Performance table: count of experimental subjects with developed tumors exhibiting the lowest metric across various models.

	BP		BPPA			BPTH
Growth Model	SSE	RMSE	MAE	SSE	RMSE	MAE	SSE	RMSE	MAE
Exponential	0	0	0	0	0	1	0	11	13
Gompertz	2	3	3	3	4	4	6	6	4
Logistic	30	29	32	8	8	6	23	21	18
Bertalanffy	4	11	9	0	0	0	7	9	7
Gaussian	0	3	0	1	1	1	7	8	8
Power law	0	3	5	1	2	3	0	3	8
Polynomial	13	0	0	3	1	1	16	1	1

addresses the growth model performance, aiming to discern the most efficient model based on a particular metric (i.e., SSE, RMSE, MAE) in the most rigorous manner.

Essentially, this elucidates the number of mice within the population with the tumor manifesting the lowest metric under the specific model, wherein a higher count signifies commendable performance. To elaborate, the polynomial model demonstrates good performance in benzopyrene, specifically for SSE. Conversely, the logistic model captures a substantial proportion of mice with tumor development across the utilized compounds. Specifically, for the BP category, ‘logistic’ identifies 30, 29, and 32 mice from a total of 49, accounting for an impressive range of 59–65%. In the case of BPPA, logistic captures 8, 8, and 6 mice from the total of 16 mice exhibiting tumor growth, constituting a substantial percentage within the range of 37–50%. Lastly, for the BPTH scenario, logistic identifies 23, 21, and 18 mice out of a total of 59 exhibiting tumor growth, representing a significant proportion within the range of 30–38%.

Expanding upon this succinct table, an additional dimension is introduced through %-tolerance measurements. These measurements afford a more lenient evaluation by considering a percentage above the minimum value of a given metric across all models. For illustrative purposes, if the logistic model yields an SSE value of 150 for a particular subject, and the Gompertz model registers 165 for the same subject, the logistic model is attributed 1 value in the growth model performance, while the Gompertz model accrues none. Taking a less stringent stance, a 5% tolerance increment is introduced. Consequently, the minimum value is recalibrated to 157.5. This adjustment maintains the status quo in the performance table. Increasing the tolerance threshold to 10% sets the minimum value at 165. Consequently, both the logistic and Gompertz models secure one value each in the growth model performance table, assuming the metric considered is the 10%-tolerance SSE.

Polynomials, in parallel, performed well in benzopyrene-based trials that relied entirely on the objective function, a pattern that was preserved for PA and TH. Bertalanffy growth models also had important outcomes in BP and BPTH settings, but were ineffective in BPPA. Gompertz contributed a tiny but consistent amount of optimal scores. The remaining models yielded little to no significant findings. These initial results (Table 4), which do not strictly correspond to the required criteria, provide a glimpse of the benefits the logistic growth model yields.

Partially studied thus far is the approximation of numerous data series and the reflection of comparable behavior; however, it remains uncertain how well or poorly the models perform in the remaining data series. Are their objective function scores close to the minimum, or do they significantly exceed it? Is the logistic model approaching the optimal value for the remaining data series, or are the results for these data subpar?

We provide %-tolerance metrics to answer these alarming concerns and assist models in meeting the previously defined standards. By using these metrics by up to forty percent, we can examine the progression of the models as the rules are gradually satisfied. This approach is not meant to advocate a departure from the most descriptive model; rather, we aim to define the algorithmic mechanisms by which that model might be precisely located. Using this strategy, several models were surprisingly more competitive than those which, despite initially appearing to outperform others, did not maintain their position or underwent a rapid increase in tumor encapsulation.

In BPPA (Figure 2), for instance, neither the exponential, Bertalanffy, nor power law models began nor ended with good scores, showing that they cannot encompass the PA response to benzopyrene double bonds. Again, polynomials had rapid growth, but ‘logistic’ and Gompertz functions considerably outpaced the competition. The later models likewise imply analogous behavior, since both the logistic model and the Gompertz model multiplied their initial population capture. Surprisingly, the 20% divergence from the minimal scores allowed the logistic model to characterize the entire NMRI population with the BPPA mixture.

In BPTH (Figure 3), the Gompertz growth model was initially second or third-to-last but managed to advance at least two spots by the time 20%-tolerance measurements were implemented. The power law, exponential, and Bertalanffy models displayed poor progression; however, the Gaussian model preserved an overall increase. The abrupt growth in polynomials followed by oscillations is suggested to be related to their overfitting character. Lastly, and most interestingly, the logistic function exhibits the same behavior across all measurements. It begins and ends first, maintaining a considerable margin above the other growth models. This culminates in a comprehensive description of the chemically induced oncogenesis encapsulation.

Therefore, anticarcinogenic drugs belonging to the PA and TH families can be exhaustively explained by adopting logistic models. By extension, the phenomena of oncogenesis inhibition can be described through their use, thereby simplifying the current perception of the chemical neutralization of malignant tumor development.

Remarkably, exponential-based models failed to account for the occurrence of chemically driven oncogenesis (Figure 4). It is probable that the adaptability offered by sigmoid functions, such as ‘logistic’, might better suit the needs of such growth. Sigmoid functions can be segmented further into linear, exponential, and plateau phases.

The first phase describes the lag period, during which the tumor does not develop rapidly; the second phase describes the exponential growth of cancer cells; and the third phase defines the transition between the exponential and plateau phases, where the tumor has reached an advanced stage where death is inevitable. No other growth model demonstrated significant potential to comprehend chemical oncogenesis. With their greatest possible outcome, no more than fifty percent of the NMRI population can be captured.

Moving on to the statistics of the model parameters following the computational pipeline of the LMA, the vast majority of parameters have CV values larger than 30%, indicating a high degree of parameter dispersion around the mean (

Table 5. Statistics of the developed model parameters.

Growth Model	Parameter	Mean ± St. Deviation	CV (%)
Bertalanffy	${\beta }_1$	2398.9 ± 13971	582.3
	${\beta }_2$	1.3569 ± 0.3655	26.9
	${\beta }_3$	0.0083 ± 0.0077	93.4
Exponential	$V_0$	265.9979 ± 306.3857	115.1
	$\lambda$	0.0495 ± 0.0837	169.2
Gaussian	a	3.90 $\times {10}^{86}$± 4.34 $\times {10}^{87}$	1113.6
	b	366.5 ± 1.364 $\times {10}^3$	372.0
	c	80.13 ± 111.45	139.0
Gompertz	$V_0$	34.7636 ± 79.4489	228.5
	A	0.3009 ± 0.2809	93.3
	B	0.0204 ± 0.0098	71.8
Logistic	A	0.0658 ± 0.0473	71.8
	B	1.161 $\times {10}^5$ ± 9.797 $\times {10}^6$	84.3
	$V_0$	51.7463 ± 80.5408	155.6
Polynomial	$p_1$	0.0153 ± 0.0184	120.1
	$p_2$	1.9384 ± 1.6870	87.0
	$p_3$	153.73 ± 169.18	110.0
	$p_4$	1.73 $\times {10}^3$ ± 1.44 $\times {10}^4$	83.7
Power law	a	1.4280 ± 7.3663	515.8
	b	5.6291 ± 9.5748	170.0

). In particular, it reveals that there is no substantial central tendency, allowing for the potential that the numbers behave arbitrarily, and further supporting the notion that models with great complexity produce flexible curves. Specifically, only the Bertalanffy $b_2$ parameter has an acceptable CV score, indicating the parameter’s centrality, range, and dispersion may be reliably replicated.

Despite scoring high in the statistical norm and considering the arbitrariness posed, it was further studied whether the associated parameters could be constrained in specific regions to facilitate faster reproducible results, permitting easier validation and assisting in locating the optimal values in the more variable parameters. Except for the Gaussian-based model, all models featured such a parameter. As a result, the parameter space of growth models is reduced by one dimension, simplifying the initial guessing procedure (

Table 6. Less varying parameter intervals.

${\mathbf{Parameter}}_{\mathbf{Growth}\mathbf{Model}}$	Interval
${{\beta }_2}_{Bertalanffy}$	$[0.9877,2.2907]$
${\lambda }_{Exponential}$	$[0,0.5169]$
$B_{Gompertz}$	$[0,0.0432]$
$A_{Logistic}$	$[0,0.3412]$
${p_1}_{Polynomial}$	$[0,0.0841]$
$a_{Powerlaw}$	$[0,2.9033]$

).

6.2. Model Predictability

Concerning model predictability, only the growth models demonstrating strong performance in the %-tolerance measurements, namely the logistic, Gaussian, and Gompertz models, were taken into account. Others are deemed incapable of adequately representing the data; hence, there is no purpose in investigating their prediction capability. From beginning to end, the employed models exhibited poor ability in predicting tumor size for the carcinogen group, as measured by a high mean difference from the ground truth. Specifically, the majority of scores were larger than 35% for the first two values (i.e., short- and medium-terms) and grew to larger than 45% for the last two (i.e., long- and extended-terms) despite the adopted model (

Table 7. Comparison of the growth model’s ability to predict different levels of the future.

Group	Growth		Mean Difference (%)
	Model	Short-Term	Medium-Term	Long-Term	Extended-Term
Carcinogen	Logistic	37.50	56.24	54.44	62.25
	Gaussian	39.65	24.04	43.71	35.47
	Gompertz	19.03	66.35	66.39	75.07
Polyamines	Logistic	0.61	11.38	29.87	53.81
	Gaussian	2.82	10.81	21.83	32.94
	Gompertz	5.76	7.72	25.39	44.89
Thiols	Logistic	3.59	13.95	18.82	23.96
	Gaussian	14.46	17.38	17.13	9.54
	Gompertz	3.76	10.22	12.96	15.71

). This behavior results from the LMA, which received the initial data points in time as input; hence, the created curve does not yet account for the exponential growth phase, resulting in a diverging curve.

In contrast, the models produced significant results when predicting the formation of tumors in anticarcinogenic substances, particularly for starting values. In both chemical combinations, the logistic model produced the smallest difference in the short-term (0.61% and 3.59%) and maintained a close relationship with the subsequent two values (PA: 11.38% and 29.87%, TH: 13.95% and 18.82%). The Gompertz and Gaussian models displayed comparable behavior, with Gompertz exhibiting marginally superior performance in both cases. All applied functions failed to accurately predict the extended term (i.e., fourth value), indicating that we can only estimate tumor growth in the near future. Consequently, the estimates are within a respectable range (about 15%) initially, but then diverge significantly. This is primarily due to the adaptability of the models and their capacity to capture changes in cancer cell growth rates, and secondarily due to the small number of recordings made during the disease’s exponential phase. Considering that the latter four values correspond to the 20- to 40-day mice tumor inspection intervals, it is plausible to conclude that human tumor growth can be precisely predicted for two years using logistic-based models (0.61%).

Utilizing the parameters derived from the LMA convergence, a classification problem was devised not only to assess their categorization properties and, by extension, the models themselves, but also to evaluate their importance in the classification task. SVM and KNN were used as the main classifiers and were fine-tuned with cross-validation accuracy serving as the objective function.

Both classifiers provide quantifiable findings and illustrate that active compounds may be distinguished, depending on model parameters exhibiting accuracy metrics above 80% across all settings (Figure 5). Specifically, all measures have satisfactory values, with the exception of the specificity metric, whose value of 54% indicates a class imbalance. Indeed, BPPA comprises 59 data points of one class compared to 16 observations of the other class; hence, additional performance metrics were utilized, such as geometric mean, F2-measure metric, and adjusted F-measure. However, the other metrics support the excellent performance of the classifier in this particular instance. It was determined not to apply more complex classifiers, such as kernel-based algorithms, because the employed approaches were effective despite their simplicity and because advanced approaches tend to overfit in small datasets, resulting in incorrect conclusions.

The ReliefF algorithm was employed to estimate the feature contribution to the classification, and the top five features are listed in

Table 8. Comparison of the growth model parameters to predict the substance group.

Classification Problem	Growth Model	Parameter	Rank	Contribution (%)
BPPA	Bertalanffy	${\beta }_2$	1	20.51
	Gaussian	c	2	18.53
	Gaussian	b	3	18.09
	Gaussian	a	4	15.37
	Bertalanffy	${\beta }_3$	5	4.98
BPAC	Logistic	A	1	34.32
	Logistic	$V_0$	2	10.17
	Exponential	$V_0$	3	8.91
	Gompertz	$V_0$	4	8.65
	Gaussian	A	5	6.20
BPTH	Logistic	A	1	27.64
	Bertalanffy	${\beta }_1$	2	25.78
	Power law	a	3	7.10
	Gompertz	$V_0$	4	6.01
	Bertalanffy	${\beta }_2$	5	5.60

. The contribution of the model parameters was computed based on the output of the relief algorithm, representing the significance of each feature (i.e., parameter) to the classification task. High values indicate a high importance, whereas low values indicate the opposite. By utilizing the importance value of each to the sum of all, it is possible to calculate a relative value that corresponds to the parameter contribution. It was unexpected that two parameters of the logistic model offer more than any other parameter from the set of development models, and their contribution is four times (44.47%) larger than the next closest in the BPAC classification task, which contains the most observations. It is particularly significant that the accounting model also ranks high for both its performance on %-tolerance metrics and its discriminant abilities.

Bertalanffy and Gaussian models dominate the contribution values above 5% in BPPA settings, with the former accumulating 25.49% and the latter 51.99%. However, the lack of data prevents us from providing reliable conclusions for this case. In comparison, logistic and Bertalanffy contribute 27.64% and 25.78%, respectively, to BPTH, whilst the remaining parameters have values of less than 7%, indicating that these models contribute significantly more to the relevant classification problem.

In addition, ANOVA was employed to determine the relative importance of the features. The contribution of each parameter and model to the BPAC classification task is depicted in Figure 6. Power law generates the largest contribution (27.34%), which is to be expected for a simple model, given that the technique harnesses the variance of the experimental populations by separating it into systematic and random variables. With values ranging from 10.23% to 15.17%, the remaining growth models contribute almost the same, indicating that they are of equal importance.

6.3. Statistical Analysis

The lifespan distribution analysis, presented in

Table 9. Assessing normality through p-values and test outcomes.

Normality Test	p-Value	Single Dose Outcome	p-Value	Single Dose Outcome
Anderson–Darling	0.0294	0	0.0133	0
Jarque–Bera	0.2254	0	0.2152	1
Lilliefors	0.1602	0	0.0237	1
Shapiro–Wilk	0.0108	0	0.0072	0

, demonstrates that single and half of the double polyamine data do not adhere to normal distributions, preventing a direct distribution comparison. This same pattern was observed in studies involving TH. To better comprehend these results, a QQ plot (Figure 7a) was generated to graphically depict the deviation of the compound mixtures from normality and to facilitate their comparison.

The straight lines represent the normal distributions of the analyzed populations with respect to the mean and standard deviations. When lines and markers are in close proximity, this indicates normality, suggesting that the compound’s behavior can be predicted and replicated with high confidence. The behavior of the blue benzopyrene line corresponds to a 95% certainty of mortality within 200 days after administrating the carcinogenic agent. There are also outliers, with one subject dying 70 days after the injection and another surviving up to 320 days.

The most major impacts are those of PA and TH. Specifically, 45% of TH markers tend to follow the benzopyrene line with a minor delay of 10 days in the lifespan axis. Within 220 days of administering the thiol-based chemical mixture, approximately 55% of the population has perished, indicating that the behavior of TH seems to match that of benzopyrene in at least half of the population, while the other half appears to be unaffected by the disease. In contrast, PA diverges from benzopyrene from the beginning to the end, exhibiting a consistent trend toward oncogenesis inhibition. Approximately 17% of the polyamine-induced mice did not make it to 220 days, which is near the expected percentage for the species. The entire population closely matches the red line of the expected distribution of PA, demonstrating that the effect of PA may be predicted more precisely.

In examining the distribution lines, benzopyrene exhibits a steep slope (70 degrees), suggesting a high incidence, leading to species endangerment. TH and PA, with angles of 23 and 25 degrees, respectively, demonstrate effectiveness against oncogenesis, differing significantly from benzopyrene. The starting points of their lines (0.025% for PA, 0.18% for TH) contrast with the 0.003% benzopyrene, indicating a greater impact. Despite TH’s asymptotic advantage, their inconsistent behavior and higher cancer prevalence raise concerns. Both PA and TH contribute to longevity; over 20% of the population exceeds the average NMRI lifespan (700 days). Therefore, these compounds not only combat cancer uniquely but also contribute to overall health.

Figure 7b illustrates a QQ plot, comparing a single dose of PA to a twofold concentration. The parallel lines signify consistent influence but with different starting points. PA exhibits a broader impact, prompting a faster response in eradicating oncogenesis. The double dose begins at a 0.02% population impact, while the single dose starts at 0.12%, suggesting a one-sixth reduction in mortality rate. Despite minor angle differences (18 and 17 degrees), deviations from the scaled population line occur consistently in both mixtures.

This suggests two key findings: firstly, the consistent population state across initial points and degrees in both experiments; and secondly, a marginal increase in outliers, indicating extended longevity due to PA. Assuming no diminishing returns, this introduces a potential avenue for inhibiting oncogenesis and promoting longevity. The Mann–Whitney U test supports the improvement claim as the double-dose PA outperforms a single-dose (p-value: 3.8 $\times {10}^5$), suggesting increased efficacy with higher concentrations. To explain these results and better capture the data tendencies, a statistical moment analysis was conducted. Mean, standard deviation, skewness, and kurtosis, also known as the first to fourth statistical moments, were adopted to assess the mortality rate or insufficient reactions of the compound mixtures (

Table 10. Statistical analysis of polyamine’s performance.

Compound Mixture	Statistical Moments				Mortality Rate (%)
	1st	2nd	3rd	4th
Benzopyrene	148.5800	1162	2.4475	13.5911	100.0
Polyamines Single Dose	475.8093	44456	−0.0697	2.1479	18.47
Difference (%)	320.23	3825	18.47
Polyamines Double Dose	593.7181	30732	0.0230	2.2980	1.34
Difference (%)	399.5	2644	1.34

).

Significantly, the average longevity improves with the increasing dosage, showing that the chemicals are more effective at higher concentrations. The standard deviation represents the degree of value dispersion around the mean, which initially varies substantially and diminishes as dosage increases. The skewness of symmetrical distributions, such as mortality distributions, should be near zero. Benzopyrene does not adhere to this criteria because of its asymmetry. PAs have a tendency to approach zero on both sides. Regarding the mortality rate, it is evident that a single dose of PA reduced the mortality rate by at least 80%; however, a double dose of PA outperformed the other mixes by producing an astounding performance in which just 1.34% of the population perished.

7. Discussion

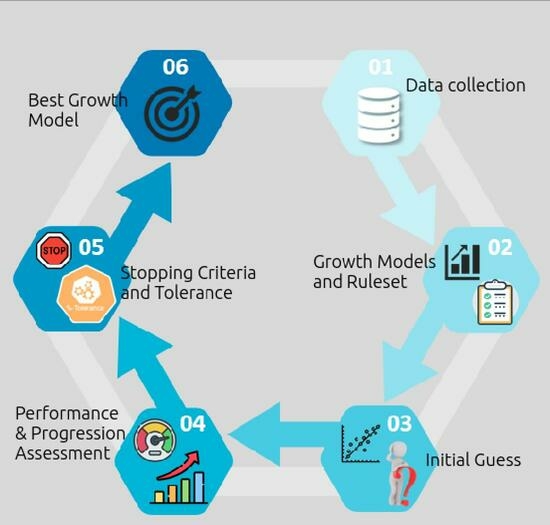
The analysis presented herein aims to explain the process of chemical oncogenesis and inhibition using mathematical functions that, when applied to data, become models. Surgical administration of benzopyrene, a chemical carcinogen capable of causing tumors with certainty, was employed to trigger chemical oncogenesis. In an effort to neutralize the carcinogenic agent, PA and TH were supplied in addition to benzopyrene to strengthen the immune system or fight cancer, respectively. These compounds, which are abundant in nature, can modify the structure of an oncogenic agent to resemble that of a less cancerous agent. In 1978, the Laboratory of Physiology at the University of Ioannina in Greece began conducting research with more than 400 NMRI subjects. These experiments led to the establishment of a dataset based on tuples consisting of tumor sizes and examination dates. The examinations were performed at specific intervals using ultrasonic tomography. Utilizing this dataset, an attempt was made to formalize an explanation workflow for the phenomena of oncogenesis and inhibition was developed (Figure 1).

However, this approach might be used in other applications that utilize past knowledge to deliver valuable insights. Initially, a rule set was designed to outline the conditions that growth models must satisfy. In this instance, three criteria were devised to evaluate the produced models and identify the one with the most descriptive power. The primary criteria synthesized involved adequately approximating various data series, reflecting comparable behavior, and avoiding fluctuations between optimal and poor outcomes. After establishing these rules, a multitude of mathematical functions were utilized to evaluate how these phenomena may be interpreted and anticipated. Sigmoid functions, which mimic homeostasis because they include linear, exponential, and plateau phases, were also used. A curve-fitting pipeline was orchestrated based on the collected data, with a focus on addressing the initial guess problem.

After LMA convergence, SSE, RMSE, and MAE served as primary performance indicators. To provide insight into model performance on the remaining data series, tolerance metrics were introduced. These metrics allowed for incremental encapsulation of model progression without sacrificing descriptiveness. In most cases, the logistic model outperformed competitors, demonstrating consistent behavior and capturing the entire population before 30%-tolerance metrics (Table 4, Figure 2, Figure 3 and Figure 4). Exploring oscillations, surprises, and abrupt growth, logistic models proved effective in explaining anticarcinogenic drugs and carcinogenic chemicals, simplifying the understanding of tumor inhibition and oncogenesis. Growth model parameters were evaluated for central tendency and parameter intervals with less variation, facilitating future reproduction and validation (Table 5 and Table 6). Logistic models excelled in forecasting tumor growth, particularly in the case of PA (Table 7). Classification problems with growth parameters as features demonstrated SVM’s superiority in distinguishing between compound combinations (Figure 5). Logistic function parameters exhibited the highest contributions in ReliefF and ANOVA in specific settings (Table 8, Figure 6). Normality tests of NMRI mortality, regardless of cancer presence, yielded inconclusive results. The factors contributing to this nature may include a relatively modest sample size, with the potential deviation of the underlying data distribution from normality, and the inherent complexity of the phenomenon under investigation, rendering it challenging to derive definitive conclusions (Table 9). For this reason, QQ plots were employed, which illustrated distinct compound combination responses and suggested the potential for a triple dosage. PA, as an alternative cancer combatant, exhibited a longer average lifespan, lower mortality rate, and stability that was positively influenced by concentration increases (Figure 7a,b).

The transition from bench-side to bedside research is illustrated by the pragmatic implications of scientific findings in oncology. Mathematical models, integrating data from surgical experiments and ultrasonic examinations, establish an algorithmic framework to understand and predict tumor behavior over time. This paradigm shift facilitates the translation of scientific insights into actionable clinical strategies, which was revealed by the experimental inclusion of PA and TH as chemopreventive measures. The developed mathematical models not only elucidate oncogenic mechanisms but also provide clinicians with practical tools for anticipating and managing tumor growth, enhancing the efficacy of cancer treatments. These models, based on tumor size and examination dates, coupled with ultrasonic tomography, are invaluable for tailoring treatment strategies, forecasting growth patterns, and optimizing therapeutic interventions. The consistent performance of the logistic model, especially in forecasting tumor growth in response to PA, signifies its transformative potential, enabling personalized treatment plans based on individual tumor dynamics and addressing complex clinical scenarios with a classification framework for compound combinations.

In contrast to previous chemoprevention-related work that either prioritized the theoretical background of compound discovery without numerical evidence or provided substantial evidence without the physiological basis for delaying or preventing cancer development, this study proposes an algorithmic pipeline of mechanisms. This pipeline uses a ruleset as a foundation to investigate the best descriptive power among a plethora of mathematical functions capable of explaining the phenomena of oncogenesis and chemical inhibition, while supporting it with chemical reaction theory. By pursuing this path, the potential to explain chemoprevention and other significant occurrences increases substantially, necessitating the selection of the most appropriate descriptive model among others. Mechanisms such as those presented can circumvent this barrier, allowing the scientific community to establish a baseline and construct more complex and seasoned schemes on top of it.

The resulting analysis is not without shortcomings and limitations. The inclusion of a modest number of ultrasonic examinations in the data collection may impact the reliability of chemoprevention outcomes. Sparse examinations, separated by over 40 days, limit insight into the precise onset of oncogenesis and its progression rate. Ethical concerns surrounding frequent exams, linked to potential cancer development from computed tomography scans, further constrain data acquisition. Additionally, the study raises concerns about heightened side effects and increased toxicity due to the novel approach of escalating compound concentrations for cancer chemical inhibition. While no subjects in this study experienced such issues, it is noteworthy that previous research reported two NMRI mice deaths attributed to probable putrescine toxicity [49]. This underscores the need for vigilant consideration of potential risks, ensuring safety and ethical integrity in experimental protocols.

In conclusion, this comprehensive discussion highlights the noteworthy contributions and limitations of the study in advancing our understanding of chemopreventive strategies and personalized cancer therapy. The developed mathematical models, incorporating PA and TH, bridge the gap between experimental and clinical realms, opening up promising avenues for cancer prevention. The logistic model’s consistent performance suggests its potential application in tailoring personalized treatment plans. Despite the challenges posed, including a modest sample size, sparse examinations, inconclusive statistical tests, and the potential toxicity produced by the chemicals, the study’s classification framework and algorithmic pipeline provide a versatile foundation for addressing complex clinical scenarios. The contextual specificity of the research design and subject characteristics must be acknowledged, as generalization challenges may restrict findings to specific populations or experimental settings. Therefore, this research not only propels the field forward but also underscores the complexities and variations inherent in studying cancer dynamics and therapeutic interventions. As we navigate these difficulties, the study lays a foundation for future investigations, emphasizing the importance of robust methodologies, ethical considerations, and a continual commitment to refining our understanding of cancer biology and treatment.

8. Conclusions

In this research article, a novel modeling methodology for chemically induced phenomena was proposed. If the study is expanded and validated in in vitro trials, it could lead to the invention of nutritional supplements that totally suppress the growth of malignant tumors, despite the adoption of healthy lifestyle choices. Synergies could also be explored in terms of their potential multiplicative benefits in the fight against malignancies. For instance, TH and PA may interact to produce an effect bigger than the total of their individual effects. However, more chemical compounds should be evaluated in this manner, producing a diverse arsenal against cancer.