Assessing Information Transmission in Data Transformations with the Channel Multivariate Entropy Triangle
Abstract
:1. Introduction
- A random source of classification labels K is subjected to a measurement process that returns random observations . The n instances of pairs is often called the (task) dataset.
- Then, a generic data transformation block may transform the available data, e.g., the observations in the dataset , into other data with “better” characteristics, the transformed feature vectors . These characteristics may be representational power, independence among individual dimensions, reduction of complexity offered to a classifier, etc. The process is normally called feature transformation and selection.
- Finally, the are the inputs to an actual classifier of choice that obtains the predicted labels .
2. Methods
2.1. The Channel Bivariate Entropy Balance Equation and Triangle
- The (normalized) redundancy ([9], Section 2.4), or divergence with respect to uniformity (yellow area), , between the joint distribution where and are independent and the uniform distributions with the same cardinality of events as and ,
- The variation of information (the sum of the red areas), [11], embodies the residual entropy, not used in binding the variables,
Application: The Evaluation of Multiclass Classification
2.2. Quantities around the Multivariate Mutual Information
- Situation 1:
- All the random variables form part of the same set , and we are looking at information transfer within this set, or
- Situation 2:
- They are partitioned into two different sets and , and we are looking at information transfer between these sets.
- Their multivariate generalization is only warranted when signed measures of probability are considered, since it is well known that some of these “areas” can be negative, contrary to the geometric intuitions in this respect.
- the interaction information [22], multivariate mutual information [23] or co-information [24] is the generalization of (9), the total amount of information to which all variables contribute.It is represented by the inner convex green area (within the dual total correlation), but note that it may in fact be negative for [25].
3. Results
3.1. The Aggregate and Split Channel Multivariate Balance Equation
- , the uniform distribution over the supports of and , and
- , the distribution created with the marginals of considered independent.
- marginal uniformity when , marginal uniformity when and marginal uniformity when both conditions coocur.
- Marginal independence, when .
- determines when , determines when and mutual determination, when both conditions hold.
- For instance, in case then after (17). Similarly, if then . Hence when marginal uniformity holds, we have .
- Similarly, when marginal independence holds, we see that from (20). Otherwise stated, and .
- Finally, if mutual determination holds—that is to say the variables in either set are deterministic functions of those of the other set—by the definition of the multivariate variation of information, we have .
- For instance, if marginal uniformity holds, then . But if marginal independence also holds, then whence by (23) .
- But if both marginal uniformity and mutual determination hold, then we have and so that .
- Finally, if both mutual determination and marginal indepence holds, then a fortiori .
3.2. Visualizations: From i-Diagrams to Entropy Triangles
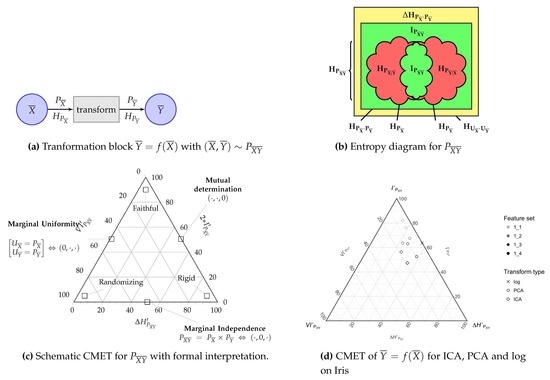
3.2.1. The Channel Multivariate Entropy Triangle
- The lower side of the triangle with , affected of marginal independence , is the locus of partitioned joint distributions who do not share information between the two blocks and .
- The right side of the triangle with , described with mutual determination , is the locus of partitioned joint distributions whose groups do not carry supplementary information to that provided by the other group.
- The left sidewith , describing distributions with uniform marginals and , is the locus of partitioned joint distributions that offer as much potential information for transformations as possible.
- If we want a transformation from to to be faithful, then we want to maximize the information used for mutual determination , equivalently, minimize at the same time the divergence from uniformity and the information that only pertains to each of the blocks in the partition . So the coordinates of a faithful partitioned joint distribution will lay close to the apex of the triangle.
- However, if the coordinates of a distribution lay close to the left vertex , then it shows marginal uniformity but shares little or no information between the blocks , hence it must be a randomizing transformation.
- Distributions whose coordinates lay close to the right vertex are essentially deterministic and in that sense carry no information . Indeed in this instance there does not seem to exist a transformation, whence we call them rigid.
3.2.2. Normalized Split Channel Multivariate Balance Equations
- The lower side of the triangle is interpreted as before.
- The right side of the triangle is the locus of the partitioned joint distribution whose block is completely determined by the block, that is, .
- The left side of the triangle is the locus of those partitioned joint distributions whose marginal is uniform .
3.3. Example Application: The Analysis of Feature Transformation and Selection with Entropy Triangles
3.4. Discussion
4. Conclusions
- We have been able to decompose the information of a random multivariate source into three components: (a) the non-transferable divergence from uniformity , which is an entropy “missing” from ; (b) a transferable, but not transferred part, the variation of information ; and (c) the transferable and transferred information , which is a known, but never considered in this context, generalization of bivariate mutual information.
- Using the same principles as in previous developments, we have been able to obtain a new type of visualization diagram for this balance of information using de Finetti’s ternary diagrams, which is actually an exploratory data analysis tool.
Author Contributions
Funding
Abbreviations
| PCA | Principal Component Analysis |
| ICA | Independent Component Analysis |
| CMET | Channel Multivariate Entropy Triangle |
| CBET | Channel Binary Entropy Triangle |
| SMET | Source Multivariate Entropy Triangle |
References
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Shwartz-Ziv, R.; Tishby, N. Opening the Black Box of Deep Neural Networks via Information. arXiv 2017, arXiv:1703.00810v3. [Google Scholar]
- Tishby, N.; Zaslavsky, N. Deep Learning and the Information Bottleneck Principle. In Proceedings of the IEEE 2015 Information Theory Workshop, San Diego, CA, USA, 1–6 February 2015. [Google Scholar]
- Valverde-Albacete, F.J.; Peláez-Moreno, C. 100% classification accuracy considered harmful: The normalized information transfer factor explains the accuracy paradox. PLOS ONE 2014. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Valverde-Albacete, F.J.; Peláez-Moreno, C. The Evaluation of Data Sources using Multivariate Entropy Tools. Expert Syst. Appl. 2017, 78, 145–157. [Google Scholar] [CrossRef]
- Valverde-Albacete, F.J.; Peláez-Moreno, C. Two information-theoretic tools to assess the performance of multi-class classifiers. Pattern Recognit. Lett. 2010, 31, 1665–1671. [Google Scholar] [CrossRef] [Green Version]
- Yeung, R. A new outlook on Shannon’s information measures. IEEE Trans. Inf. Theory 1991, 37, 466–474. [Google Scholar] [CrossRef]
- Reza, F.M. An Introduction to Information Theory; McGraw-Hill Electrical and Electronic Engineering Series; McGraw-Hill Book Co., Inc.: New York, NY, USA; Toronto, ON, Canada; London, UK, 1961. [Google Scholar]
- MacKay, D.J.C. Information Theory, Inference and Learning Algorithms; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, XXVII, 379–423, 623–656. [Google Scholar] [CrossRef]
- Meila, M. Comparing clusterings—An information based distance. J. Multivar. Anal. 2007, 28, 875–893. [Google Scholar] [CrossRef]
- Pawlowsky-Glahn, V.; Egozcue, J.J.; Tolosana-Delgado, R. Modeling and Analysis of Compositional Data; John Wiley & Sons: Chichester, UK, 2015. [Google Scholar]
- Valverde-Albacete, F.J.; de Albornoz, J.C.; Peláez-Moreno, C. A Proposal for New Evaluation Metrics and Result Visualization Technique for Sentiment Analysis Tasks. In CLEF 2013: Information Access Evaluation. Multilinguality, Multimodality and Visualization; Forner, P., Müller, H., Paredes, R., Rosso, P., Stein, B., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; Volume 8138, pp. 41–52. [Google Scholar]
- Timme, N.; Alford, W.; Flecker, B.; Beggs, J.M. Synergy, redundancy, and multivariate information measures: An experimentalist’s perspective. J. Comput. Neurosci. 2014, 36, 119–140. [Google Scholar] [CrossRef] [PubMed]
- James, R.G.; Ellison, C.J.; Crutchfield, J.P. Anatomy of a bit: Information in a time series observation. Chaos 2011, 21, 037109. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Watanabe, S. Information theoretical analysis of multivariate correlation. J. Res. Dev. 1960, 4, 66–82. [Google Scholar] [CrossRef]
- Tononi, G.; Sporns, O.; Edelman, G.M. A measure for brain complexity: Relating functional segregation and integration in the nervous system. Proc. Natl. Acad. Sci. USA 1994, 91, 5033–5037. [Google Scholar] [CrossRef] [PubMed]
- Studený, M.; Vejnarová, J. The Multiinformation Function as a Tool for Measuring Stochastic Dependence. In Learning in Graphical Models; Springer: Dordrecht, The Netherlands, 1998; pp. 261–297. [Google Scholar]
- Han, T.S. Nonnegative entropy measures of multivariate symmetric correlations. Inf. Control 1978, 36, 133–156. [Google Scholar] [CrossRef]
- Abdallah, S.A.; Plumbley, M.D. A measure of statistical complexity based on predictive information with application to finite spin systems. Phys. Lett. A 2012, 376, 275–281. [Google Scholar] [CrossRef] [Green Version]
- Tononi, G. Complexity and coherency: Integrating information in the brain. Trends Cognit. Sci. 1998, 2, 474–484. [Google Scholar] [CrossRef]
- McGill, W.J. Multivariate information transmission. Psychometrika 1954, 19, 97–116. [Google Scholar] [CrossRef]
- Sun Han, T. Multiple mutual informations and multiple interactions in frequency data. Inf. Control 1980, 46, 26–45. [Google Scholar] [CrossRef]
- Bell, A. The co-information lattice. In Proceedings of the Fifth International Workshop on Independent Component Analysis and Blind Signal Separation, Nara, Japan, 1–4 April 2003. [Google Scholar]
- Abdallah, S.A.; Plumbley, M.D. Predictive Information, Multiinformation and Binding Information; Technical Report C4DM-TR10-10; Queen Mary, University of London: London, UK, 2010. [Google Scholar]
- Valverde Albacete, F.J.; Peláez-Moreno, C. The Multivariate Entropy Triangle and Applications. In Hybrid Artificial Intelligence Systems (HAIS 2016); Springer: Seville, Spain, 2016; pp. 647–658. [Google Scholar]
- Witten, I.H.; Eibe, F.; Hall, M.A. Data Mining. Practical Machine Learning Tools and Techniques, 3rd ed.; Morgan Kaufmann: Burlington, MA, USA, 2011. [Google Scholar]
- Pearson, K. On Lines and Planes of Closest Fit to Systems of Points in Space. Philos. Mag. 1901, 559–572. [Google Scholar] [CrossRef]
- Bell, A.J.; Sejnowski, T.J. An Information-Maximization Approach to Blind Separation and Blind Deconvolution. Neural Comput. 1995, 7, 1129–1159. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hyvärinen, A.; Oja, E. Independent component analysis: Algorithms and applications. IEEE Trans. Neural Netw. 2000, 13, 411–430. [Google Scholar] [CrossRef]
- Bache, K.; Lichman, M. UCI Machine Learning Repository; 2013. [Google Scholar]
- Gu, G.; Fogla, P.; Dagon, D.; Lee, W.; Skorić, B. Measuring Intrusion Detection Capability: An Information- theoretic Approach. In Proceedings of the 2006 ACM Symposium on Information, Computer and Communications Security (ASIACCS ’06), Taipei, Taiwan, 21–23 March 2006; ACM: New York, NY, USA, 2006; pp. 90–101. [Google Scholar] [CrossRef]
- James, G.R.; Crutchfield, P.J. Multivariate Dependence beyond Shannon Information. Entropy 2017, 19, 531–545. [Google Scholar] [CrossRef]
- Jizba, P.; Arimitsu, T. The world according to Rényi: Thermodynamics of multifractal systems. Ann. Phys. 2004, 312, 17–59. [Google Scholar] [CrossRef]







| Name | k | m | n | |
|---|---|---|---|---|
| 1 | Ionosphere | 2 | 34 | 351 |
| 2 | Iris | 3 | 4 | 150 |
| 3 | Glass | 7 | 9 | 214 |
| 4 | Arthritis | 3 | 3 | 84 |
| 5 | BreastCancer | 2 | 9 | 699 |
| 6 | Sonar | 2 | 60 | 208 |
| 7 | Wine | 3 | 13 | 178 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Valverde-Albacete, F.J.; Peláez-Moreno, C. Assessing Information Transmission in Data Transformations with the Channel Multivariate Entropy Triangle. Entropy 2018, 20, 498. https://doi.org/10.3390/e20070498
Valverde-Albacete FJ, Peláez-Moreno C. Assessing Information Transmission in Data Transformations with the Channel Multivariate Entropy Triangle. Entropy. 2018; 20(7):498. https://doi.org/10.3390/e20070498
Chicago/Turabian StyleValverde-Albacete, Francisco J., and Carmen Peláez-Moreno. 2018. "Assessing Information Transmission in Data Transformations with the Channel Multivariate Entropy Triangle" Entropy 20, no. 7: 498. https://doi.org/10.3390/e20070498
APA StyleValverde-Albacete, F. J., & Peláez-Moreno, C. (2018). Assessing Information Transmission in Data Transformations with the Channel Multivariate Entropy Triangle. Entropy, 20(7), 498. https://doi.org/10.3390/e20070498