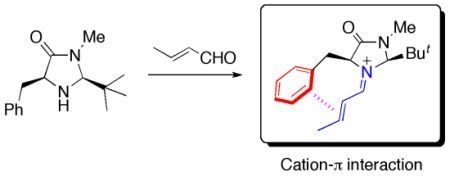
Contribution of Cation-π Interactions in Iminium Catalysis
Abstract
:1. Introduction


2. Results and Discussion
2.1. Conformational Preferences in Iminium Intermediate 1 and Related Species 2–5

| B3LYP | MP2 | HF | C4 a -- C ipso | C4 a -- C ortho | |
|---|---|---|---|---|---|
| 1A | 0.00 b | 0.00 | 0.00 | 3.34 | 3.51 |
| 1B | 0.91 b | 2.00 | 0.32 | 3.89 | 3.97 |
| 2A | 0.00 b | 0.00 | 0.00 | 3.47 | 3.57 |
| 2B | −0.38 b | 0.86 | −0.64 | 4.11 | 4.23 |
| 3A | 0.00 | 0.00 | 0.00 | 3.33 | 3.56 |
| 3B | 1.09 | 2.33 | 0.53 | 3.82 | 3.93 |
| 4A | 0.00 | 0.00 | 0.00 | 3.35 | 3.52 |
| 4B | 0.74 | 1.75 | 0.00 | 3.89 | 3.99 |
| 5Ac | 0.00 | − | − | 3.29 | 3.48 |
| 5Bc | 1.03 | − | − | 3.77 | 3.83 |

2.2. Origin of Interaction between the Iminium and Phenyl Moieties

| M1A | M1B | M2A | M3A | M4A | |
|---|---|---|---|---|---|
| E(MP2) a | −5.32 | −3.60 | −0.30 | −6.58 | −3.44 |
| E(HF) a | 0.08 | −1.08 | 4.81 | −0.47 | 2.32 |
| E(correlation) b | −5.40 | −2.52 | −5.10 | −6.10 | −5.76 |
| E(electrostatic) | −4.34 | −0.58 | −2.09 | − | − |
| E(polarization) | −3.05 | −2.50 | −0.35 | − | − |
| E(charge transfer) | −2.10 | −1.39 | −1.41 | − | − |
| E(exchange repulsion) | 7.86 | 2.36 | 7.49 | − | − |
| E(others) | 0.91 | 0.54 | 0.30 | − | − |
| BSSE | 0.81 | 0.48 | 0.87 | − | − |
| Transferred charge c | 0.08e | 0.02 | 0.01 | 0.09 | 0.08 |
3. Computational Details
4. Conclusions
Supplementary Materials
Supplementary File 1Acknowledgements
References and Notes
- Ahrendt, K.A.; Borths, C.J.; MacMillan, D.W.C. New strategies for organic catalysis: The first highly enantioselective organocatalytic Diels-Alder reaction. J. Am. Chem. Soc. 2000, 122, 4243–2444. [Google Scholar]
- Paras, N.A.; MacMillan, D.W.C. New strategies in organic catalysis: The first enantioselective organocatalytic Friedel-Crafts alkylation. J. Am. Chem. Soc. 2001, 123, 4370–4371. [Google Scholar]
- Austin, J.F.; MacMillan, D.W.C. Enantioselective organocatalytic indole alkylations. Design of a new highly effective chiral amine for iminium catalysis. J. Am. Chem. Soc. 2002, 124, 1172–1173. [Google Scholar]
- Paras, N.A.; MacMillan, D.W.C. The enantioselective organocatalytic 1,4-addition of electron-rich benzenes to α, β-unsaturated aldehydes. J. Am. Chem. Soc. 2002, 124, 7894–7895. [Google Scholar]
- Wilson, R.A.; Jen, W.S.; MacMillan, D.W.C. Enantioselective organocatalytic intramolecular Diels-Alder reactions. The asymmetric synthesis of Solanapyrone D. J. Am. Chem. Soc. 2005, 127, 11616–11617. [Google Scholar] [CrossRef]
- Jen, W.S.; Wiener, J.J.M.; MacMillan, D.W.C. New strategies for organic catalysis: The first enantioselective organocatalytic 1,3-Dipolar cycloaddition. J. Am. Chem. Soc. 2000, 122, 9874–9875. [Google Scholar] [CrossRef]
- Gordillo, R.; Carter, J.; Houk, K.N. Theoretical explorations of enantioselective alkylation reactions of pyrroles and indoles organocatalyzed by chiral imidazolidinones. Adv. Synth. Catal. 2004, 346, 1175–1185. [Google Scholar] [CrossRef]
- Allemann, C.; Gordillo, R.; Clemente, F.R.; Cheong, P.H.; Houk, K.N. Theory of asymmetric organocatalysis of aldol and related reactions: Rationalizations and predictions. Acc. Chem. Res. 2004, 37, 558–569. [Google Scholar] [CrossRef]
- Yamada, S.; Fossey, J. Nitrogen cation-pi interactions in asymmetric organocatalytic synthesis. Org. Biomol. Chem. 2011, 9, 7275–7281. [Google Scholar] [CrossRef]
- Cheong, P.H.-Y.; Legault, C.Y.; Um, J.M.; Celebi-Ölcüm, N.; Houk, K.N. Quantum mechanical investigations of organocatalysis: Mechanisms, reactivities, and selectivities. Chem. Rev. 2011, 111, 5042–5137. [Google Scholar] [CrossRef]
- Morokuma, K.; Kitaura, K. A new energy decomposition scheme for molecular interactions within Hartree-Fock approximation. Int. J. Quantum Chem. 1976, 10, 325–340. [Google Scholar] [CrossRef]
- Tsuzuki, S.; Mikami, M.; Yamada, S. Origin of attraction, magnitude, and directionality of interactions in benzene complexes with pyridiunium cations. 2007. [Google Scholar]
- According to Refereence [12], the MP2 method overestimates the correlation effects typically by ca. 30% compared with the more accurate CCSD(T) method at the basis set limit. On the other hand, use of small basis set underestimates the correlation energy compared with the value at the basis set limit. In the present calculations at the MP2 level with medium-size basis set, these errors could be partially cancelled out. Thus, the relative correlation energies in the present series are believed to be correct at least qualitatively.
- Singh, U.C.; Kollman, P.A. An approach to computing electrostatic charges for molecules. J. Comput. Chem. 1984, 5, 129–145. [Google Scholar]
- Besler, B.H.; Merz, K.M.; Kollman, P.A. Atomic charges derived from semiempirical methods. J. Comput. Chem. 1990, 111, 431–439. [Google Scholar]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; Nakatsuji, H.; Caricato, M.; Li, X.; Hratchian, H.P.; Izmaylov, A.F.; Bloino, J.; Zheng, G.; Sonnenberg, J.L.; Hada, M.; Ehara, M.; Toyota, K.; Fukuda, R.; Hasegawa, J.; Ishida, M.; Nakajima, T.; Honda, Y.; Kitao, O.; Nakai, H.; Vreven, T.; Montgomery, J.A., Jr.; Peralta, J.E.; Ogliaro, F.; Bearpark, M.; Heyd, J.J.; Brothers, E.; Kudin, K.N.; Staroverov, V.N.; Kobayashi, R.; Normand, J.; Raghavachari, K.; Rendell, A.; Burant, J.C.; Iyengar, S.S.; Tomasi, J.; Cossi, M.; Rega, N.; Millam, N.J.; Klene, M.; Knox, J.E.; Cross, J.B.; Bakken, V.; Adamo, C.; Jaramillo, J.; Gomperts, R.; Stratmann, R.E.; Yazyev, O.; Austin, A.J.; Cammi, R.; Pomelli, C.; Ochterski, J.W.; Martin, R.L.; Morokuma, K.; Zakrzewski, V.G.; Voth, G.A.; Salvador, P.; Dannenberg, J.J.; Dapprich, S.; Daniels, A.D.; Farkas, Ö.; Foresman, J.B.; Ortiz, J.V.; Cioslowski, J.; Fox, D.J. Gaussian 03; Gaussian, Inc.: Wallingford CT, USA, 2003. [Google Scholar]
- Schmidt, M.W.; Baldridge, K.K.; Boatz, J.A.; Elbert, S.T.; Gordon, M.S.; Jensen, J.J.; Koseki, S.; Matsunaga, N.; Nguyen, K.A.; Su, S.; et al. General atomic and molecular electronic structure system. J. Comput. Chem. 1993, 14, 1347–1363. [Google Scholar]
- Sample Availability: Not available.
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Mori, Y.; Yamada, S. Contribution of Cation-π Interactions in Iminium Catalysis. Molecules 2012, 17, 2161-2168. https://doi.org/10.3390/molecules17022161
Mori Y, Yamada S. Contribution of Cation-π Interactions in Iminium Catalysis. Molecules. 2012; 17(2):2161-2168. https://doi.org/10.3390/molecules17022161
Chicago/Turabian StyleMori, Yukie, and Shinji Yamada. 2012. "Contribution of Cation-π Interactions in Iminium Catalysis" Molecules 17, no. 2: 2161-2168. https://doi.org/10.3390/molecules17022161
APA StyleMori, Y., & Yamada, S. (2012). Contribution of Cation-π Interactions in Iminium Catalysis. Molecules, 17(2), 2161-2168. https://doi.org/10.3390/molecules17022161