Molecular Simulation of the Separation of Isoleucine Enantiomers by β-Cyclodextrin
Abstract
:1. Introduction
2. Results and Discussion
2.1. Molecular Mechanics Simulation
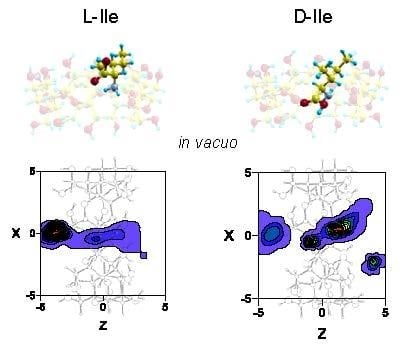
2.2. Molecular Dynamics Simulation
3. Materials and Methods
3.1. Molecular Mechanics Simulation
3.2. Molecular Dynamics Simulation
4. Conclusions
Funding
Conflicts of Interest
References
- Szejtli, J.; Osa, T. Comprehensive Supramolecular Chemistry; Pergamon/Elsevier: Oxford, UK, 1996. [Google Scholar]
- Lipkowitz, K.B. Atomistic modeling of enantioselection in chromatography. J. Chromatogr. A 2001, 906, 417–442. [Google Scholar] [CrossRef]
- Lipkowitz, K.B. Applications of computational chemistry to the study of cyclodextrins. Chem. Rev. 1998, 98, 1829–1873. [Google Scholar] [CrossRef]
- Maier, N.M.; Franco, P.; Lindner, W. Separation of enantiomers: Needs, challenges, perspectives. J. Chromatogr. A 2001, 906, 3–33. [Google Scholar] [CrossRef]
- Ramanathan, R.; Prokai, L. Electrospray ionization mass spectrometric study of encapsulation of amino acids by cyclodextrins. J. Am. Soc. Mass Spectrom. 1995, 6, 866–871. [Google Scholar] [CrossRef] [Green Version]
- Boniglia, C.; Carratù, B.; Sanzini, E. Enantiomer separation of D-L branched amino acids by capillary electrophoresis in sport nutritional supplements. J. Food Sci. 2002, 67, 1352–1355. [Google Scholar] [CrossRef]
- Roy, M.N.; Roy, A.; Saha, S. Probing inclusion complexes of cyclodextrins with amino acids by physicochemical approach. Carbohydr. Polym. 2016, 151, 458–466. [Google Scholar] [CrossRef]
- Ramirez, J.; Ahn, S.; Grigorean, G.; Lebrilla, C.B. Evidence for the formation of gas-phase inclusion complexes with cyclodextrins and amino acids. J. Am. Chem. Soc. 2000, 122, 6884–6890. [Google Scholar] [CrossRef]
- Alvira, E. Molecular dynamics study of the influence of solvents on the chiral discrimination of alanine enantiomers by β-cyclodextrin. Tetrahedron Asymmetry 2013, 24, 1198–1206. [Google Scholar] [CrossRef]
- Alvira, E. Theoretical study of the separation of valine enantiomers by β-cyclodextrin with different solvents: A molecular mechanics and dynamics simulation. Tetrahedron Asymmetry 2015, 26, 1198–1206. [Google Scholar] [CrossRef]
- Alvira, E. Influence of valine enantiomer configuration on the molecular dynamics simulation of their separation by β-cyclodextrin. Chem. Phys. Lett. 2017, 679, 31–37. [Google Scholar] [CrossRef]
- Alvira, E. Influence of solvent polarity on the separation of leucine enantiomers by β-cyclodextrin: A molecular mechanics and dynamics simulation. Tetrahedron Asymmetry 2017, 28, 1414–1422. [Google Scholar] [CrossRef]
- Weiner, S.J.; Kollman, P.A.; Case, D.A.; Singh, U.C.; Ghio, C.; Alagona, G.; Profeta, S., Jr.; Weiner, P.J. A new force field for molecular mechanical simulation of nucleic acids and proteins. J. Am. Chem. Soc. 1984, 106, 765–784. [Google Scholar] [CrossRef]
- Weiner, S.J.; Kollman, P.A.; Nguyen, D.T.; Case, D.A. An all atom force field for simulations of proteins and nucleic acids. J. Comput. Chem. 1986, 7, 230–252. [Google Scholar] [CrossRef]
- Kokalj, A. Computer graphics and graphical user interfaces as tools in simulations of matter at the atomic scale. Comput. Mater. Sci. 2003, 28, 155–168. [Google Scholar] [CrossRef]
- Lipkowitz, K.B.; Pearl, G.; Coner, B.; Peterson, M.A. Explanation of where and how enantioselective binding takes place on permethylated β-cyclodextrin, a chiral stationary phase used in gas chromatography. J. Am. Chem. Soc. 1997, 119, 600–610. [Google Scholar] [CrossRef]
- Lipkowitz, K.B.; Coner, B.; Peterson, M.A. Locating regions of maximum chiral discrimination: A computational study of enantioselection on a popular chiral stationary phase used in chromatography. J. Am. Chem. Soc. 1997, 119, 11269–11276. [Google Scholar] [CrossRef]
- Kinglert, B.; Rihs, G.J. Molecular encapsulation of transition metal complexes in cyclodextrins. Part 3. Structural consequences of varying the guest geometry in channel-type inclusion compounds. J. Chem. Soc. Dalton Trans. 1991, 0, 2749–2760. [Google Scholar]
- Lindorff-Larsen, K.; Piana, S.; Palmo, K.; Maragakis, P.; Klepeis, J.L.; Dror, R.O.; Shaw, D.E. Improved side-chain torsion potentials for the AMBER ff99SB protein force field. Proteins 2010, 78, 1950–1958. [Google Scholar] [CrossRef]
- Werner, H.-J.; Knowles, P.J.; Knizia, G.; Manby, F.R.; Schütz, M. Molpro: A general-purpose quantum chemistry program package. WIREs Comput. Mol. Sci. 2012, 2, 242–253. [Google Scholar] [CrossRef]
- Werner, H.-J.; Knowles, P.J.; Knizia, G.; Manby, F.R.; Schütz, M. (Eds.) MOLPRO, version 2012.1; a package of ab initio programs; TGZ Molpro: Stuttgart, Germany, 2012. [Google Scholar]
- Alvira, E. Theoretical study of the β-cyclodextrin inclusion complex formation of eugenol in water. Molecules 2018, 23, 928. [Google Scholar] [CrossRef]
- Brown, D.; Clarke, J.H.R. A comparison of constant energy, constant temperature and constant pressure ensembles in molecular dynamics simulations of atomic liquids. Mol. Phys. 1984, 51, 1243–1248. [Google Scholar] [CrossRef]
- Fincham, D.; Quirke, N.; Tildesley, D.J. Computer simulation of molecular liquid mixtures. I. A diatomic Lennard-Jones model mixture for CO2/C2H6. J. Chem. Phys. 1986, 84, 4535–4541. [Google Scholar] [CrossRef]
- Frenkel, D.; Smit, B. Understanding Molecular Simulation; Academic Press: San Diego, CA, USA, 2002. [Google Scholar]
- Rapaport, D.C. The Art of Molecular Dynamics Simulation; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Allen, M.P.; Tildesley, D.J. Computer Simulation of Liquids; Clarendon Press: Oxford, UK, 1987. [Google Scholar]
Sample Availability: Samples of the compounds are not available from the authors. |






| Con. | ε | Emin (kcal/mol) | ELJ (kcal/mol) | Eele (kcal/mol) | EH-bond (kcal/mol) | Ebond (kcal/mol) | Eangle (kcal/mol) | Etorsion (kcal/mol) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| L | D | L | D | L | D | L | D | L | D | L | D | L | D | ||
| NP | 1 | −10.91 | −10.81 | −11.89 | −13.60 | −7.38 | −5.67 | 0.00 | 0.00 | 1.45 | 1.52 | 4.76 | 4.81 | 2.15 | 2.12 |
| NP | 2 | −8.32 | −8.02 | −14.20 | −13.87 | −2.06 | −2.61 | −0.49 | 0.00 | 1.54 | 1.52 | 4.74 | 4.81 | 2.15 | 2.12 |
| NP | 21 | −6.71 | −6.70 | −14.81 | −14.68 | 0.13 | 0.02 | −0.46 | −0.49 | 1.57 | 1.57 | 4.71 | 4.76 | 2.15 | 2.12 |
| NP | 26 | −6.73 | −6.71 | −14.81 | −14.68 | 0.10 | 0.02 | −0.46 | −0.49 | 1.57 | 1.57 | 4.71 | 4.76 | 2.15 | 2.12 |
| P | 21 | −8.32 | −7.40 | −14.80 | −13.85 | −0.43 | −0.82 | 0.00 | −0.49 | 1.49 | 1.43 | 3.27 | 4.21 | 2.15 | 2.12 |
| P | 26 | −8.24 | −7.29 | −14.80 | −14.30 | −0.34 | −0.28 | 0.00 | −0.50 | 1.48 | 1.48 | 3.27 | 4.19 | 2.15 | 2.12 |
| P | 80 | −8.09 | −7.10 | −14.93 | −14.30 | −0.08 | −0.09 | 0.00 | −0.50 | 1.52 | 1.48 | 3.25 | 4.19 | 2.15 | 2.12 |
| Con. | ε | Number of Trajectories | Fmean (kcal/mol) | Elution Order | tmean (ps) | |||
|---|---|---|---|---|---|---|---|---|
| L | D | L | D | L | D | |||
| NP | 1 | 15 | 17 | −9.77 | −12.22 | L | 751.11 | ts |
| NP | 2 | 16 | 16 | −9.45 | −10.87 | L | 1098.18 | ts |
| NP | 21 | 16 | 17 | −7.82 | −8.17 | L | 659.62 | 675.35 |
| NP | 26 | 16 | 16 | −7.48 | −8.00 | L | 789.68 | 672.56 |
| P | 21 | 13 | 14 | −8.84 | −9.24 | L | 837.56 | 1212.11 |
| P | 26 | 14 | 18 | −8.73 | −9.18 | L | 554.58 | 1300.17 |
| P | 80 | 17 | 16 | −8.67 | −8.70 | L | 557.25 | 818.16 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alvira, E. Molecular Simulation of the Separation of Isoleucine Enantiomers by β-Cyclodextrin. Molecules 2019, 24, 1021. https://doi.org/10.3390/molecules24061021
Alvira E. Molecular Simulation of the Separation of Isoleucine Enantiomers by β-Cyclodextrin. Molecules. 2019; 24(6):1021. https://doi.org/10.3390/molecules24061021
Chicago/Turabian StyleAlvira, Elena. 2019. "Molecular Simulation of the Separation of Isoleucine Enantiomers by β-Cyclodextrin" Molecules 24, no. 6: 1021. https://doi.org/10.3390/molecules24061021
APA StyleAlvira, E. (2019). Molecular Simulation of the Separation of Isoleucine Enantiomers by β-Cyclodextrin. Molecules, 24(6), 1021. https://doi.org/10.3390/molecules24061021