Adsorption in Mixtures with Competing Interactions
Abstract
:1. Introduction
2. The Model and the Simulation Method
2.1. The Model
2.2. The Simulation Method
3. Results
3.1. Effect of Wall–Particle Interactions on Distribution of Particles near a Selective Substrate
3.1.1. The One-Component System with SALR Interactions
3.1.2. The Binary Mixture
3.2. Effect of Gas Density and Surface Selectivity on the Adsorption and Selective Adsorption
4. Summary and Discussion
- The presence of the second component has a huge effect on the adsorption of the first-component particles.
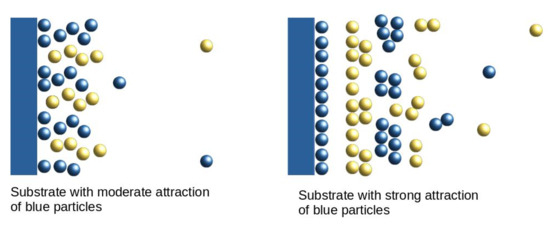
- The distribution of the particles near the substrate depends qualitatively on the strength of the attraction of the first-component particles to the substrate; the alternating layers of the two component particles are perpendicular to the substrate with moderate attraction (Figure 3), and parallel to the substrate with strong attraction (Figure 4). In the latter case, an ordered internal structure in the parallel layers is present.
- Despite the repulsion of the second component from the substrate, comparable amounts of the particles of the two components are adsorbed.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
Sample Availability
References
- Dash, J.G. Films on Solid Surfaces: The Physics and Chemistry of Physical Adsorption; Elsevier: Amsterdam, The Netherlands, 1975. [Google Scholar]
- Jerome, B. Surface effects and anchoring in liquid crystals. Rep. Prog. Phys. 1991, 54, 391. [Google Scholar] [CrossRef]
- Netz, R.R.; Andelman, D. Neutral and charged polymers at interfaces. Phys. Rep. 2003, 380, 1–95. [Google Scholar] [CrossRef] [Green Version]
- Rabe, M.; Verdes, D.; Seeger, S. Physical Adsorption: Forces and Phenomena; Dover Publications: New York, NY, USA, 2011. [Google Scholar]
- Stradner, A.; Sedgwick, H.; Cardinaux, F.; Poon, W.; Egelhaaf, S.; Schurtenberger, P. Equilibrium cluster formation in concentrated protein solutions and colloids. Nature 2004, 432, 492. [Google Scholar] [CrossRef] [Green Version]
- Campbell, A.I.; Anderson, V.J.; van Duijneveldt, J.S.; Bartlett, P. Dynamical Arrest in Attractive Colloids: The Effect of Long-Range Repulsion. Phys. Rev. Lett. 2005, 94, 208301. [Google Scholar] [CrossRef] [Green Version]
- Ciach, A.; Pȩkalski, J.; Góźdź, W.T. Origin of similarity of phase diagrams in amphiphilic and colloidal systems with competing interactions. Soft Matter 2013, 9, 6301. [Google Scholar] [CrossRef] [Green Version]
- Royall, C.P. Hunting mermaids in real space: Known knowns, known unknowns and unknown unknowns. Soft Matter 2018, 14, 4020. [Google Scholar] [CrossRef] [Green Version]
- Zhuang, Y.; Zhang, K.; Charbonneau, P. Equilibrium Phase Behavior of a Continuous-Space Microphase Former. Phys. Rev. Lett. 2016, 116, 098301. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Edelmann, M.; Roth, R. Gyroid phase of fluids with spherically symmetric competing interactions. Phys. Rev. E 2016, 93, 062146. [Google Scholar] [CrossRef] [PubMed]
- Pini, D.; Parola, A. Pattern formation and self-assembly driven by competing interactions. Soft Matter 2017, 13, 9259. [Google Scholar] [CrossRef] [Green Version]
- Lindquist, B.A.; Jadrich, R.B.; Truskett, T.M. Assembly of nothing: Equilibrium fluids with designed structrued porosity. Soft Matter 2016, 12, 2663–2667. [Google Scholar] [CrossRef] [Green Version]
- Litniewski, M.; Ciach, A. Effect of aggregation on adsorption phenomena. J. Chem. Phys. 2019, 150, 234702. [Google Scholar] [CrossRef]
- Bildanau, E.; Pȩkalski, J.; Vikhrenko, V.; Ciach, A. Adsorption anomalies in a 2D model of cluster-forming systems. Phys. Rev. E 2020, 101, 012801. [Google Scholar] [CrossRef] [Green Version]
- Ciach, A. Combined density functional and Brazovskii theories for systems with spontaneous inhomogeneities. Soft Matter 2018, 14, 5497. [Google Scholar] [CrossRef] [Green Version]
- Ciach, A. Universal sequence of ordered structures obtained from mesoscopic description of self-assembly. Phys. Rev. E 2008, 78, 061505. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Santos, A.P.; Pȩkalski, J.; Panagiotopoulos, A.Z. Thermodynamic signatures and cluster properties of self-assembly in systems with competing interactions. Soft Matter 2017, 13, 8055–8063. [Google Scholar] [CrossRef]
- Santos, A.P.; Panagiotopoulos, A.Z. Determination of the critical micelle concentration in simulations of surfactant systems. J. Chem. Phys. 2016, 144, 044709. [Google Scholar] [CrossRef] [Green Version]
- Leunissen, M.; Christova, C.; Hynninen, A.P.; Royal, C.; Campbell, A.; Imhof, A.; Dijkstra, M.; van Roji, R.; van Blaaderen, A. Ionic colloidal crystals of oppositely charged particles. Nature 2005, 437, 235. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bartlett, P.; Campbell, A.I. Three-Dimensional Binary Superlattices of Oppositely Charged Colloids. Phys. Rev. Lett. 2005, 95. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Patsahan, O.; Meyra, A.; Ciach, A. Correlation functions in mixtures with energetically favoured nearest neighbours of different kind: A size-asymmetric case. Mol. Phys. 2020, 1–16. [Google Scholar] [CrossRef]
- Ciach, A.; Patsahan, O.; Meyra, A. Effects of fluctuations on correlation functions in inhomogeneous mixtures. Condens. Matter Phys. 2020, 23, 23601. [Google Scholar] [CrossRef]
- Patsahan, O.; Litniewski, M.; Ciach, A. Self-assembly in mixtures with competing interactions. Soft Matter 2021, 17, 2883. [Google Scholar] [CrossRef]
- Hertlein, C.; Helden, L.; Gambassi, A.; Dietrich, S.; Bechinger, C. Direct measurement of critical Casimir forces. Nature 2008, 451, 172. [Google Scholar] [CrossRef]
- Gambassi, A.; Maciołek, A.; Hertlein, C.; Nellen, U.; Helden, L.; Bechinger, C.; Dietrich, S. Critical Casimir effect in classical binary liquid mixtures. Phys. Rev. E 2009, 80, 061143. [Google Scholar] [CrossRef] [Green Version]
- Pousaneh, F.; Ciach, A.; Maciołek, A. How ions in solution can change the sign of the critical Casimir potential. Soft Matter 2014, 10, 470. [Google Scholar] [CrossRef] [Green Version]
- Marolt, K.; Zimmermann, M.; Roth, R. Microphase separation in a two-dimensional colloidal system with competing attractive critical Casimir and repulsive magnetic dipole interactions. Phys. Rev. E 2019, 100, 052602. [Google Scholar] [CrossRef] [PubMed]
- Marolt, K.; Roth, R. Statics and dynamics of a finite two-dimensional colloidal system with competing attractive critical Casimir and repulsive magnetic dipole interactions. Phys. Rev. E 2020, 102, 042608. [Google Scholar] [CrossRef] [PubMed]
- Vasilyev, O.A.; Marino, E.; Kluft, B.B.; Schall, P.; Kondrat, S. Debye vs. Casimir: Controlling the structure of charged nanoparticles deposited on a substrate. Nanoscale 2021, 113, 6475. [Google Scholar] [CrossRef]
- Serna, H.; Pozuelo, A.D.; Noya, E.G.; Góźdź, W.T. Formation and internal ordering of periodic microphases in colloidal models with competing interactions. Soft Matter 2021, 17, 4957. [Google Scholar] [CrossRef] [PubMed]
- Shelke, P.B.; Nguyen, V.D.; Limaye, A.V.; Schall, P. Controlling Colloidal Morphologies by Critical Casimir Forces. Adv. Mater. 2013, 25, 1499. [Google Scholar] [CrossRef]
- Allen, M.P.; Tildesley, D.J. Computer Simulations of Liquids; Clarendon Press: Oxford, UK, 1990. [Google Scholar]
- Brazovskii, S.A. Phase transition of an isotropic system to a nonuniform state. Sov. Phys. JETP 1975, 41, 85. [Google Scholar]








Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Litniewski, M.; Ciach, A. Adsorption in Mixtures with Competing Interactions. Molecules 2021, 26, 4532. https://doi.org/10.3390/molecules26154532
Litniewski M, Ciach A. Adsorption in Mixtures with Competing Interactions. Molecules. 2021; 26(15):4532. https://doi.org/10.3390/molecules26154532
Chicago/Turabian StyleLitniewski, Marek, and Alina Ciach. 2021. "Adsorption in Mixtures with Competing Interactions" Molecules 26, no. 15: 4532. https://doi.org/10.3390/molecules26154532
APA StyleLitniewski, M., & Ciach, A. (2021). Adsorption in Mixtures with Competing Interactions. Molecules, 26(15), 4532. https://doi.org/10.3390/molecules26154532