Hydration Dynamics and the Future of Small-Amplitude AFM Imaging in Air
Abstract
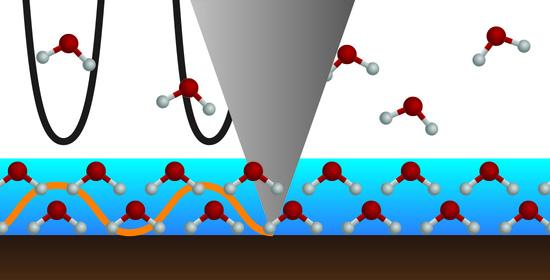
:1. Introduction
2. Discussion
2.1. The Problem of Small Amplitude Imaging and Surface Aging
2.2. Force Reconstruction and Imaging
2.3. Other Possible Dynamic Parameters to Consider
3. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hansma, P.K.; Cleveland, J.P.; Radmacher, M.; Walters, D.A.; Hillner, P.E.; Bezanilla, M.; Fritz, M.; Vie, D.; Hansma, H.G.; Prater, C.B.; et al. Tapping mode atomic force microscopy in liquids. Appl. Phys. Lett. 1994, 64, 1738–1740. [Google Scholar] [CrossRef]
- García, R.; Paulo, A.S. Attractive and repulsive tip-sample interaction regimes in tapping-mode atomic force microscopy. Phys. Rev. B 1999, 60, 4961–4967. [Google Scholar] [CrossRef] [Green Version]
- Eichhorn, A.L.; Dietz, C. Simultaneous Deconvolution of In-Plane and Out-of-Plane Forces of HOPG at the Atomic Scale under Ambient Conditions by Multifrequency Atomic Force Microscopy. Adv. Mater. Interfaces 2021, 8, 2101288. [Google Scholar] [CrossRef]
- Gauthier, M.; Pérez, R.; Arai, T.; Tomitori, M.; Tsukada, M. Interplay between Nonlinearity, Scan Speed, Damping, and Elec-tronics in Frequency Modulation Atomic-Force Microscopy. Phys. Rev. Lett. 2002, 89, 146104. [Google Scholar] [CrossRef] [Green Version]
- Rana, S.; Pota, H.; Petersen, I.R. A Survey of Methods Used to Control Piezoelectric Tube Scanners in High-Speed AFM Imaging. Asian J. Control. 2018, 20, 1379–1399. [Google Scholar] [CrossRef]
- Garcí, R.; Perez, R. Dynamic atomic force microscopy methods. Surf. Sci. Rep. 2002, 47, 197–301. [Google Scholar] [CrossRef]
- Ortega-Esteban, A.; Gonzalez, F.; Martin, N.; de Fablo, P. Structural and mechanical characterization of viruses with AFM. In Atomic Force Microscopy. Methods in Molecular Biology; Humana Press: New York, NY, USA, 2019; Volume 1886, pp. 259–278. [Google Scholar]
- Garcia, R. Nanomechanical mapping of soft materials with the atomic force microscope: Methods, theory and applications. Chem. Soc. Rev. 2020, 49, 5850–5884. [Google Scholar] [CrossRef]
- Ramos, J.R. Tip radius preservation for high resolution imaging in amplitude modulation atomic force microscopy. Appl. Phys. Lett. 2014, 105, 43111. [Google Scholar] [CrossRef]
- Trinidad, E.R.; Gribnau, T.W.; Belardinelli, P.; Staufer, U.; Alijani, F. Nonlinear dynamics for estimating the tip radius in atomic force microscopy. Appl. Phys. Lett. 2017, 111, 123105. [Google Scholar] [CrossRef]
- Hernández-Muñoz, J.; Uhlig, M.R.; Benaglia, S.; Chacón, E.; Tarazona, P.; García, R. Subnanometer Interfacial Forces in Three-Dimensional Atomic Force Microscopy: Water and Octane near a Mica Surface. J. Phys. Chem. C 2020, 124, 26296–26303. [Google Scholar] [CrossRef]
- Uhlig, M.R.; Benaglia, S.; Thakkar, R.; Comer, J.; Garcia, R. Atomically resolved interfacial water structures on crystalline hy-drophilic and hydrophobic surfaces. Nanoscale 2021, 13, 5275–5283. [Google Scholar] [CrossRef]
- Fukuma, T.; Ueda, Y.; Yoshioka, S.; Asakawa, H. Atomic-Scale Distribution of Water Molecules at the Mica-Water Interface Visualized by Three-Dimensional Scanning Force Microscopy. Phys. Rev. Lett. 2010, 104, 16101. [Google Scholar] [CrossRef] [Green Version]
- Jiao, F.; Cannon, K.S.; Lin, Y.-C.; Gladfelter, A.S.; Scheuring, S. The hierarchical assembly of septins revealed by high-speed AFM. Nat. Commun. 2020, 11, 1–13. [Google Scholar] [CrossRef]
- Stilp, F.; Bereczuk, A.; Berwanger, J.; Mundigl, N.; Richter, K.; Giessibl, F.J. Very weak bonds to artificial atoms formed by quantum corrals. Science 2021, 372, 1196–1200. [Google Scholar] [CrossRef]
- Uhlig, M.R.; Garcia, R. In Situ Atomic-Scale Imaging of Interfacial Water under 3D Nanoscale Confinement. Nano Lett. 2021, 21, 5593–5598. [Google Scholar] [CrossRef]
- Calò, A.; Robles, O.V.; Santos, S.; Verdaguer, A. Capillary and van der Waals interactions on CaF2 crystals from amplitude modulation AFM force reconstruction profiles under ambient conditions. Beilstein J. Nanotechnol. 2015, 6, 809–819. [Google Scholar] [CrossRef] [Green Version]
- Lacasa, J.S.; Almonte, L.; Colchero, J. In situ characterization of nanoscale contaminations adsorbed in air using atomic force microscopy. Beilstein J. Nanotechnol. 2018, 9, 2925–2935. [Google Scholar] [CrossRef]
- Wastl, D.S.; Weymouth, A.; Giessibl, F. Optimizing atomic resolution of force microscopy in ambient conditions. Phys. Rev. B 2013, 87, 245415. [Google Scholar] [CrossRef]
- Giessibl, F.J. AFM’s path to atomic resolution. Mater. Today 2005, 8, 32–41. [Google Scholar] [CrossRef]
- Santos, S.; Barcons, V.; Christenson, H.K.; Billingsley, D.J.; Bonass, W.A.; Font, J.; Thomson, N.H. Stability, resolution, and ultra-low wear amplitude modulation atomic force microscopy of DNA: Small am-plitude small set-point imaging. Appl. Phys. Lett. 2013, 103, 63702–63705. [Google Scholar] [CrossRef] [Green Version]
- Zitzler, L.; Herminghaus, S.; Mugele, F. Capillary forces in tapping mode atomic force microscopy. Phys. Rev. B 2002, 66, 155436. [Google Scholar] [CrossRef] [Green Version]
- Leroch, S.; Wendland, M. Influence of Capillary Bridge Formation onto the Silica Nanoparticle Interaction Studied by Grand Canonical Monte Carlo Simulations. Langmuir 2013, 29, 12410–12420. [Google Scholar] [CrossRef] [PubMed]
- Sahagún, E.; García-Mochales, P.; Sacha, G.; Sáenz, J.J. Energy dissipation due to capillary interactions: Hydrophobicity maps in force microscopy. Phys. Rev. Lett. 2007, 98, 176106. [Google Scholar] [CrossRef] [Green Version]
- Yaminsky, V. The hydrophobic force: The constant volume capillary approximation. Colloids Surf. A Physicochem. Eng. Asp. 1999, 159, 181–195. [Google Scholar] [CrossRef]
- Yang, Q.; Sun, P.Z.; Fumagalli, L.; Stebunov, Y.V.; Haigh, S.J.; Zhou, Z.W.; Grigorieva, I.V.; Wang, F.C.; Geim, A.K. Capillary condensation under atomic-scale confinement. Nature 2020, 588, 250–253. [Google Scholar] [CrossRef]
- Amadei, C.A.; Tang, T.C.; Chiesa, M.; Santos, S. The aging of a surface and the evolution of conservative and dissipative na-noscale interactions. J. Chem. Phys. 2013, 139, 84708. [Google Scholar] [CrossRef]
- Klasen, A.; Baumli, P.; Sheng, Q.; Johannes, E.; Bretschneider, S.A.; Hermes, I.M.; Bergmann, V.W.; Gort, C.; Axt, A.; Weber, S.A.L.; et al. Removal of Surface Oxygen Vacancies Increases Conductance Through TiO2 Thin Films for Perovskite Solar Cells. J. Phys. Chem. 2019, 123, 13458–13466. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Zhu, X.; Chu, C.; Xiao, X.; Chen, B. Applications of atomic force microscopy-based imaging and force spectroscopy in assessing environmental interfacial processes. Crit. Rev. Environ. 2021, 1–32. [Google Scholar] [CrossRef]
- Lu, J.-Y.; Lai, C.-Y.; Almansoori, I.; Chiesa, M. The evolution in graphitic surface wettability with first-principles quantum simulations: The counterintuitive role of water. Phys. Chem. Chem. Phys. 2018, 20, 22636–22644. [Google Scholar] [CrossRef] [Green Version]
- Alshehhi, M.; Alhassan, S.M.; Chiesa, M. Dependence of surface aging on DNA topography investigated in attractive bimodal atomic force microscopy. Phys. Chem. Chem. Phys. 2017, 19, 10231–10236. [Google Scholar] [CrossRef]
- Santos, S. Enhanced sensitivity and contrast with bimodal atomic force microscopy with small and ultra-small amplitudes in ambient conditions. Appl. Phys. Lett. 2013, 103, 231603. [Google Scholar] [CrossRef] [Green Version]
- Lai, C.-Y.; Santos, S.; Chiesa, M. Systematic Multidimensional Quantification of Nanoscale Systems from Bimodal Atomic Force Microscopy Data. ACS Nano 2016, 10, 6265–6272. [Google Scholar] [CrossRef]
- Chiesa, M.; Lai, C.-Y. Surface aging investigation by means of an AFM-based methodology and the evolution of conservative nanoscale interactions. Phys. Chem. Chem. Phys. 2018, 20, 19664–19671. [Google Scholar] [CrossRef] [Green Version]
- Santos, S.; Amadei, C.A.; Lai, C.-Y.; Olukan, T.; Lu, J.-Y.; Font, J.; Barcons, V.; Verdaguer, A.; Chiesa, M. Investigating the Ubiquitous Presence of Nanometric Water Films on Surfaces. J. Phys. Chem. C 2021, 125, 15759–15772. [Google Scholar] [CrossRef]
- Giessibl, F.J. Advances in atomic force microscopy. Rev. Mod. Phys. 2003, 75, 949–983. [Google Scholar] [CrossRef] [Green Version]
- Verdaguer, A.; Sacha, G.M.; Bluhm, A.H.; Salmeron, M. Molecular Structure of Water at Interfaces: Wetting at the Nanometer Scale. Chem. Rev. 2006, 106, 1478–1510. [Google Scholar] [CrossRef]
- Henderson, M. The interaction of water with solid surfaces: Fundamental aspects revisited. Surf. Sci. Rep. 2002, 46, 1–308. [Google Scholar] [CrossRef]
- Israelachvili, J.N. Intermolecular and Surface Forces; Elsevier Academic Press: London, UK, 2005. [Google Scholar]
- Amadei, C.A.; Lai, C.-Y.; Heskes, D.; Chiesa, M. Time dependent wettability of graphite upon ambient exposure: The role of water adsorption. J. Chem. Phys. 2014, 141, 84709. [Google Scholar] [CrossRef]
- Sader, J.E.; Jarvis, S.P. Accurate formulas for interaction force and energy in frequency modulation force spectroscopy. Appl. Phys. Lett. 2004, 84, 1801–1803. [Google Scholar] [CrossRef] [Green Version]
- Katan, A.; Van Es, M.H.; Oosterkamp, T.H. Quantitative force versus distance measurements in amplitude modulation AFM: A novel force inversion technique. Nanotechnology 2009, 20, 165703. [Google Scholar] [CrossRef]
- Amir, F.P.; Martin-Jimenez, D.; Garcia, R. Force reconstruction from tapping mode force microscopy experiments. Nanotechnology 2015, 26, 185706. [Google Scholar]
- Hu, S.; Raman, A. Inverting amplitude and phase to reconstruct tip–sample interaction forces in tapping mode atomic force microscopy. Nanotechnology 2008, 19, 375704. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Huber, F.; Giessibl, F. Experimental demonstration of pitfalls and remedies for precise force deconvolution in frequency-modulation atomic force microscopy. arXiv 2020, arXiv:2001.11323. [Google Scholar]
- Sader, J.E.; Sanelli, J.A.; Adamson, B.; Monty, J.; Wei, X.; Crawford, S.A.; Friend, J.; Marusic, I.; Mulvaney, P.; Bieske, E. Spring constant calibration of atomic force microscope cantilevers of arbitrary shape. Rev. Sci. Instrum. 2012, 83, 103705. [Google Scholar] [CrossRef] [Green Version]
- Lai, C.-Y.; Tang, T.-C.; Amadei, C.A.; Marsden, A.J.; Verdaguer, A.; Wilson, N.; Chiesa, M. A nanoscopic approach to studying evolution in graphene wettability. Carbon 2014, 80, 784–792. [Google Scholar] [CrossRef]
- García, R.; Paulo, A.S. Dynamics of a vibrating tip near or in intermittent contact with a surface. Phys. Rev. B 2000, 61, R13381–R13384. [Google Scholar] [CrossRef] [Green Version]
- Santos, S. Dynamic Atomic Force Microscopy and Applications in Biomolecular Imaging; University of Leeds: Leeds, UK, 2011; Available online: https://etheses.whiterose.ac.uk/1910/ (accessed on 7 October 2021).
- Barcons, V.; Santos, S.; Bonass, W.; Font, J.; Thomson, N.H. Mono-stability of sharp tips interacting with surface hydration layers. arXiv 2015, arXiv:1506.03961. [Google Scholar]
- Santos, S.; Guang, L.; Souier, T.; Gadelrab, K.; Chiesa, M.; Thomson, N.H. A method to provide rapid in situ determination of tip radius in dynamic atomic force microscopy. Rev. Sci. Instrum. 2012, 83, 43707. [Google Scholar] [CrossRef]
- Santos, S.; Barcons, V.; Font, J.; Thomson, N.H. Bi-stability of amplitude modulation AFM in air: Deterministic and stochastic outcomes for imaging biomolecular systems. Nanotechnology 2010, 21, 225710. [Google Scholar] [CrossRef]
- Santos, S. Phase contrast and operation regimes in multifrequency atomic force microscopy. Appl. Phys. Lett. 2014, 104, 143109. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Ramírez-Hinestrosa, S.; Dobnikar, J.; Frenkel, D. The Lennard-Jones potential: When (not) to use it. Phys. Chem. Chem. Phys. 2020, 22, 10624–10633. [Google Scholar] [CrossRef] [Green Version]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Santos, S.; Olukan, T.A.; Lai, C.-Y.; Chiesa, M. Hydration Dynamics and the Future of Small-Amplitude AFM Imaging in Air. Molecules 2021, 26, 7083. https://doi.org/10.3390/molecules26237083
Santos S, Olukan TA, Lai C-Y, Chiesa M. Hydration Dynamics and the Future of Small-Amplitude AFM Imaging in Air. Molecules. 2021; 26(23):7083. https://doi.org/10.3390/molecules26237083
Chicago/Turabian StyleSantos, Sergio, Tuza A. Olukan, Chia-Yun Lai, and Matteo Chiesa. 2021. "Hydration Dynamics and the Future of Small-Amplitude AFM Imaging in Air" Molecules 26, no. 23: 7083. https://doi.org/10.3390/molecules26237083
APA StyleSantos, S., Olukan, T. A., Lai, C. -Y., & Chiesa, M. (2021). Hydration Dynamics and the Future of Small-Amplitude AFM Imaging in Air. Molecules, 26(23), 7083. https://doi.org/10.3390/molecules26237083