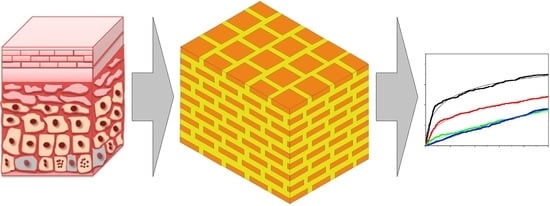
The New Attempt at Modeling of the Three-Dimensional Geometry of the Epidermal Skin Layer and the Diffusion Processes of Nanomolecular Drug Carriers in Such Structures
Abstract
:1. Introduction
2. Modeling Considerations
2.1. Capillary Model of Stratum Corneum
2.2. Model of a Diffusion Process of Nanoparticles
3. Numerical Simulation of the Diffusion Processes
4. Results of the Numerical Experiments and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Biswas, P.; Wu, C.-Y. Nanoparticles and the Environment. J. Air Waste Manag. Assoc. 2005, 55, 708–746. [Google Scholar] [CrossRef] [PubMed]
- Smita, S.; Gupta, S.K.; Bartonova, A.; Dusinska, M.; Gutleb, A.C.; Rahman, Q. Nanoparticles in the environment: Assessment using the causal diagram approach. Environ. Health 2012, 11, 13. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Waghule, T.; Rapalli, V.K.; Gorantla, S.; Saha, R.N.; Dubey, S.K.; Puri, A.; Singhvi, G. Nanostructured Lipid Carriers as Potential Drug Delivery Systems for Skin Disorders. Curr. Pharm. Des. 2020, 26, 4569–4579. [Google Scholar] [CrossRef] [PubMed]
- Beck, R.; Guterres, S.; Pohlmann, A. Nanocosmetics and Nanomedicines New Approaches for Skin Care; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Verma, A.; Jain, A.; Hurkat, P.; Jain, S.K. Transfollicular drug delivery: Current perspectives. Res. Rep. Transderm. Drug Deliv. 2016, 5, 1–17. [Google Scholar]
- Olejnik, A.; Semba, J.A.; Kulpa, A.; Danczak-Pazdrowska, A.; Dalibor Rybka, J.; Gornowicz-Porowska, J. 3D Bioprinting in Skin Related Research: Recent Achievements and Application Perspectives. ACS Synth. Biol. 2022, 11, 26–38. [Google Scholar] [CrossRef] [PubMed]
- Schmitt, T.; Neubert, R.H.H. State of the art in Stratum Corneum research: The biophysical properties of ceramides. Chem. Phys. Lipids 2018, 216, 91–103. [Google Scholar] [CrossRef] [PubMed]
- Błaszczyk, M.M.; Sęk, J.; Przybysz, Ł. The Combined Diffusion and Adsorption Concept for Prediction of Nanoparticles Transport through Dermal Layers Based on Experiments in Membranes. Int. J. Mol. Sci. 2022, 23, 6419. [Google Scholar] [CrossRef] [PubMed]
- Wu, W.; Wang, Z.; Wu, Y.; Wu, H.; Chen, T.; Xue, Y.; Wang, Y.; Jiang, C.; Shen, C.; Liu, L.; et al. Mechanisms of Penetration Enhancement and Transport Utilizing Skin Keratine Liposomes for the Topical Delivery of Licochalcone A. Molecules 2022, 27, 2504. [Google Scholar] [CrossRef] [PubMed]
- Palmer, B.C.; DeLouise, L.A. Nanoparticle-Enabled Transdermal Drug Delivery Systems for Enhanced Dose Control and Tissue Targeting. Molecules 2016, 21, 1719. [Google Scholar] [CrossRef] [Green Version]
- Schneider, M.; Stracke, F.; Hansen, S.; Schaefer, U. Nanoparticles and their interactions with the dermal barrier. Derm. -Endocrinol. 2009, 1, 197–206. [Google Scholar] [CrossRef] [Green Version]
- Aquines, O.; Saavedra-Hernández, A.; Urbina-Arias, N.; Melchor-Martínez, E.M.; Sosa-Hernández, J.E.; Robledo-Padilla, F.; Iqbal, H.M.N.; Parra-Saldívar, R. In Silico Modeling Study of Curcumin Diffusion and Cellular Growth. Appl. Sci. 2022, 12, 9749. [Google Scholar] [CrossRef]
- Borrego-Sánchez, A.; Debnath, J.; Parrinello, M. Kinetics of Drug Release from Clay Using Enhanced Sampling Methods. Pharmaceutics 2022, 14, 2586. [Google Scholar] [CrossRef]
- Available online: https://www.comsol.com/comsol-multiphysics (accessed on 20 September 2022).
- Available online: https://www.comsol.com/particle-tracing-module (accessed on 20 September 2022).
- Conzelmann, N.A.; Part, M.N.; Clemens, F.J.; Müller, C.R.; Poulikakos, L.D. Effect of artificial aggregate shapes on the porosity, tortuosity and permeability of their packings. Powder Technol. 2022, 397, 117019. [Google Scholar] [CrossRef]
- Peijie, Y.; Huihui, S.; Hairui, M.; Wuchao, Y.; Zhi, H.; Xiaonan, Z. The modification of the Kozeny-Carman equation through the lattice Boltzmann simulation and experimental verification. J. Hydrol. 2022, 609, 127738. [Google Scholar] [CrossRef]
- Richardson, J.F.; Harker, J.H.; Backhurst, R. Flow of Fluids through Granular Beds and Packed Columns, 5th ed.; Chemical Engineering Series; Volume 2 Particle Technology and Separation Processes; Butterworth Heinemann: Oxford, UK, 2002; pp. 191–236. [Google Scholar]
- Karagiorgis, S.; Tsamis, A.; Voutouri, C.; Turcu, R.; Porav, S.A.; Socoliuc, V.; Vekas, L.; Louca, M.; Stylianopoulos, T.; Vavourakis, V.; et al. Engineered magnetoactive collagen hydrogels with tunable and predictable mechanical response. Mater. Sci. Eng. C 2020, 114, 111089. [Google Scholar] [CrossRef] [PubMed]
- Kruczek, B. Carman–Kozeny Equation. In Encyclopedia of Membranes; Drioli, E., Giorno, L., Eds.; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar] [CrossRef]
- Larese, F.F.; D’Agostin, F.; Crosera, M.; Adami, G.; Renzi, N.; Bovenzi, M.; Maina, G. Human skin penetration of silver nanoparticles through intact and damaged skin. Toxicology 2009, 255, 33–37. [Google Scholar] [CrossRef] [PubMed]
- Tak, Y.; Pal, S.; Naoghare, P.; Rangasamy, S.; Song, J.M. Shape-Dependent Skin Penetration of Silver Nanoparticles: Does It Really Matter? Sci. Rep. 2015, 5, 16908. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gupta, R.; Rai, B. Effect of Size and Surface Charge of Gold Nanoparticles on their Skin Permeability: A Molecular Dynamics Study. Sci. Rep. 2017, 7, 45292. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Römgens, A.M.; Bader, D.L.; Bouwstra, J.A.; Baaijens, F.P.; Oomens, C.W. Diffusion profile of macromolecules within and between human skin layers for (trans)dermal drug delivery. J. Mech. Behav. Biomed. Mater. 2015, 50, 215–222. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schulz, R.; Kenji Yamamoto, K.; Klossek, A.; Rancan, F.; Vogt, A.; Schütte, C.; Rühl, E.; Netz, R.R. Modeling of Drug Diffusion Based on Concentration Profiles in Healthy and Damaged Human Skin. Biophys. J. 2019, 117, 998–1008. [Google Scholar] [CrossRef]







| d∙109 m | Deff ·1013 (m2/s) | n (−) | ||||
|---|---|---|---|---|---|---|
| η 10 mPa∙s | η 20 mPa∙s | η 50 mPa∙s | η 10 mPa∙s | η 20 mPa∙s | η 50 mPa∙s | |
| 1 (R2) | 21.9 (0.987) | 16.2 (0.990) | 10.1 (0.989) | 0.581 | 0.557 | 0.734 |
| 5 (R2) | 8.96 (0.991) | 5.41 (0.992) | 2.14 (0.983) | 0.557 | 0.491 | 0.889 |
| 10 (R2) | 5.54 (0.982) | 4.36 (0.989 | 1.33 (0.984) | 0.863 | 0.561 | 0.697 |
| 15 (R2) | 5.04 (0.993) | 2.54 (0.991) | 2.36 (0.985) | 1.159 | 0.958 | 0.907 |
| d∙109 m | η = 10 mPa∙s | η = 20 mPa∙s | η = 50 mPa∙s | |||
|---|---|---|---|---|---|---|
| D 1013 (m2/s) | D/Deff | D 1013 (m2/s) | D/Deff | D 1013 (m2/s) | D/Deff | |
| 1 | 21.5 | 9.79 | 107 | 6.62 | 42.9 | 4.24 |
| 5 | 4.29 | 4.79 | 21.5 | 3.96 | 8.58 | 4.01 |
| 10 | 2.15 | 4.25 | 10.7 | 2.46 | 4.29 | 3.22 |
| 15 | 1.43 | 2.56 | 7.15 | 2.81 | 2.86 | 1.21 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Błaszczyk, M.M.; Sęk, J.P. The New Attempt at Modeling of the Three-Dimensional Geometry of the Epidermal Skin Layer and the Diffusion Processes of Nanomolecular Drug Carriers in Such Structures. Molecules 2023, 28, 205. https://doi.org/10.3390/molecules28010205
Błaszczyk MM, Sęk JP. The New Attempt at Modeling of the Three-Dimensional Geometry of the Epidermal Skin Layer and the Diffusion Processes of Nanomolecular Drug Carriers in Such Structures. Molecules. 2023; 28(1):205. https://doi.org/10.3390/molecules28010205
Chicago/Turabian StyleBłaszczyk, Mariola M., and Jerzy P. Sęk. 2023. "The New Attempt at Modeling of the Three-Dimensional Geometry of the Epidermal Skin Layer and the Diffusion Processes of Nanomolecular Drug Carriers in Such Structures" Molecules 28, no. 1: 205. https://doi.org/10.3390/molecules28010205
APA StyleBłaszczyk, M. M., & Sęk, J. P. (2023). The New Attempt at Modeling of the Three-Dimensional Geometry of the Epidermal Skin Layer and the Diffusion Processes of Nanomolecular Drug Carriers in Such Structures. Molecules, 28(1), 205. https://doi.org/10.3390/molecules28010205