3D Conformational Generative Models for Biological Structures Using Graph Information-Embedded Relative Coordinates
Abstract
:1. Introduction
2. Results and Discussion
2.1. The Advantage of Using GIE-RC for Structure Reconstruction
2.2. Accuracy of Graph-AE for Conformation Reconstruction on Different Datasets
2.3. Conformation Generation through Latent Space Interpolation
2.4. Structure Augmentation for Neural Network-Based Force Field Constructions
3. Methods and Materials
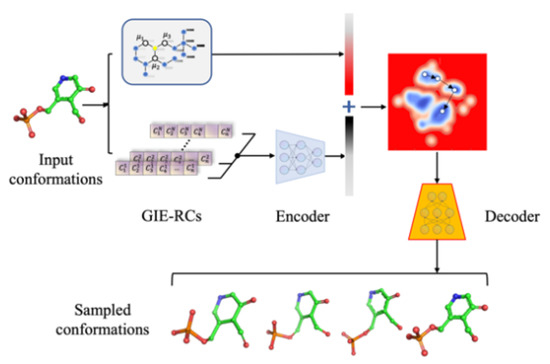
3.1. Generating Graph Information-Embedded Relative Coordinate (GIE-RC) for Molecular Conformation
- (1)
- The binary 2D adjacent matrix of a molecule is converted to a weighted graph distance matrix by first calculating the shortest bond distance between the atom pair using the Dijkstra algorithm [37], then summing the standard bond length in the MMFF94 force field [38] as the distance of the atom pair in the graph. In this way, the element in the matrix is the weighted bond distance between the atom pair.
- (2)
- A Coulomb matrix [39] is constructed based on the weighted graph distance matrix , the element of the matrix , as defined in Equation (1):where is the atomic number of atoms and is the 2D weighted graph distance between atom and . Then, a unique order of atoms is determined by sorting the eigen values [] of Coulomb matrix M.
- (3)
- Calculation of the relative coordinates of neighbor atoms within three bond distances of center atom . Here, atoms a and (as shown in Figure 9) are the closest atoms to atom i in the weighted 2D graph. If there are atoms which have the same distance to atom i, their order is decided based on the order . is the relative coordinate of atom j in the local coordinate system determined by and defined in Equation (2):where {} are the local 3D coordinates of atom in the atom centered coordinate system. is the weighted 2D graph distance between atom and j. is an attenuation factor defined in Equation (3), ensuring that the contribution of distant atoms to the relative coordinates is gradually reduced to 0. and are user defined cut-off value set to 5.0 and 6.0, respectively, in the current study.
- (4)
- Aggregate the RCs of neighboring atoms around central atom to obtain the local structure feature (ie. GIE-RC) as the environment feature for atom , which represents the local environment of atom . The RCs of local structure feature are sorted by the weighted graph distance to atom in increasing order.
- (5)
- All atomic environment features () are sorted by the standard order and compose a unique feature tensor F to represent the conformation, named as the graph information-embedded relative coordinate matrix (GIE-RCM). After the encoding process, every molecular conformation can be represented by a set of atomic environment features {}, i.e., refers to the local structure feature of atom .
3.2. Graph Constrained Autoencoder Model for Structure Generation
3.3. Datasets and Computational Settings
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Sample Availability
References
- Scheraga, H.A.; Khalili, M.; Liwo, A. Protein-Folding Dynamics: Overview of Molecular Simulation Techniques. Annu. Rev. Phys. Chem. 2007, 58, 57–83. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, C.; Chou, K. Monte Carlo simulation studies on the prediction of protein folding types from amino acid composition. Biophys. J. 1992, 63, 1523–1529. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sugita, Y.; Okamoto, Y. Replica-exchange molecular dynamics method for protein folding. Chem. Phys. Lett. 1999, 314, 141–151. [Google Scholar] [CrossRef]
- So/rensen, M.R.; Voter, A. Temperature-accelerated dynamics for simulation of infrequent events. J. Chem. Phys. 2000, 112, 9599–9606. [Google Scholar] [CrossRef] [Green Version]
- Laio, A.; Parrinello, M. Escaping free-energy minima. Proc. Natl. Acad. Sci. USA 2002, 99, 12562–12566. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Demuynck, R.; Wieme, J.; Rogge, S.M.J.; Dedecker, K.D.; Vanduyfhuys, L.; Waroquier, M.; Van Speybroeck, V. Protocol for Identifying Accurate Collective Variables in Enhanced Molecular Dynamics Simulations for the Description of Structural Transformations in Flexible Metal–Organic Frameworks. J. Chem. Theory Comput. 2018, 14, 5511–5526. [Google Scholar] [CrossRef]
- Hooft, F.; Ortíz, A.P.D.A.; Ensing, B. Discovering Collective Variables of Molecular Transitions via Genetic Algorithms and Neural Networks. J. Chem. Theory Comput. 2021, 17, 2294–2306. [Google Scholar] [CrossRef]
- Ribeiro, J.M.L.; Bravo, P.; Wang, Y.; Tiwary, P. Reweighted autoencoded variational Bayes for enhanced sampling (RAVE). J. Chem. Phys. 2018, 149, 072301. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.; Wang, H.; Weinan, E. Reinforced dynamics for enhanced sampling in large atomic and molecular systems. J. Chem. Phys. 2018, 148, 124113. [Google Scholar] [CrossRef]
- Zhang, J.; Yang, Y.I.; Noé, F. Targeted Adversarial Learning Optimized Sampling. J. Phys. Chem. Lett. 2019, 10, 5791–5797. [Google Scholar] [CrossRef]
- Zhang, J.; Lei, Y.-K.; Yang, Y.I.; Gao, Y.Q. Deep learning for variational multiscale molecular modeling. J. Chem. Phys. 2020, 153, 174115. [Google Scholar] [CrossRef] [PubMed]
- Noé, F.; Olsson, S.; Köhler, J.; Wu, H. Boltzmann generators: Sampling equilibrium states of many-body systems with deep learning. Science 2019, 365, eaaw1147. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tunyasuvunakool, K.; Adler, J.; Wu, Z.; Green, T.; Zielinski, M.; Žídek, A.; Bridgland, A.; Cowie, A.; Meyer, C.; Laydon, A.; et al. Highly accurate protein structure prediction for the human proteome. Nature 2021, 596, 590–596. [Google Scholar] [CrossRef] [PubMed]
- Cramer, P. AlphaFold2 and the future of structural biology. Nat. Struct. Mol. Biol. 2021, 28, 704–705. [Google Scholar] [CrossRef] [PubMed]
- Xu, M.; Yu, L.; Song, Y.; Shi, C.; Ermon, S.; Tang, J. GeoDiff: A Geometric Diffusion Model for Molecular Conformation Generation. arXiv 2022, arXiv:2203.02923. [Google Scholar]
- Kuzminykh, D.; Polykovskiy, D.; Kadurin, A.; Zhebrak, A.; Baskov, I.; Nikolenko, S.; Shayakhmetov, R.; Zhavoronkov, A. 3D Molecular Representations Based on the Wave Transform for Convolutional Neural Networks. Mol. Pharm. 2018, 15, 4378–4385. [Google Scholar] [CrossRef] [Green Version]
- Xu, M.; Luo, S.; Bengio, Y.; Peng, J.; Tang, J. Learning neural generative dynamics for molecular conformation generation. arXiv 2021, arXiv:2102.10240. [Google Scholar]
- Masuda, T.; Ragoza, M.; Koes, D.R. Generating 3d molecular structures conditional on a receptor binding site with deep generative models. arXiv 2020, arXiv:2010.14442. [Google Scholar]
- Winter, R.; Noé, F.; Clevert, D.-A. Auto-Encoding Molecular Conformations. arXiv 2021, arXiv:2101.01618. [Google Scholar]
- Li, Y.; Pei, J.; Lai, L. Structure-based de novo drug design using 3D deep generative models. Chem. Sci. 2021, 12, 13664–13675. [Google Scholar] [CrossRef]
- Roney, J.P.; Maragakis, P.; Skopp, P.; Shaw, D.E. Generating Realistic 3D Molecules with an Equivariant Conditional Likelihood Model. In Proceedings of the Tenth International Conference on Learning Representations, Virtual, 25–29 April 2022. [Google Scholar]
- Gebauer, N.W.A.; Gastegger, M.; Hessmann, S.S.P.; Müller, K.-R.; Schütt, K.T. Inverse design of 3d molecular structures with conditional generative neural networks. arXiv 2021, arXiv:2109.04824. [Google Scholar] [CrossRef] [PubMed]
- Luo, Y.; Ji, S. An Autoregressive Flow Model for 3D Molecular Geometry Generation from Scratch. In Proceedings of the Tenth International Conference on Learning Representations, Virtual, 26 April 2022. [Google Scholar]
- Ganea, O.-E.; Pattanaik, L.; Coley, C.W.; Barzilay, R.; Jensen, K.F.; Green, W.H.; Jaakkola, T.S. GeoMol: Torsional Geometric Generation of Molecular 3D Conformer Ensembles. arXiv 2021, arXiv:2106.07802. [Google Scholar]
- Gilmer, J.; Schoenholz, S.S.; Riley, P.F.; Vinyals, O.; Dahl, G.E. Neural Message Passing for Quantum Chemistry. In Proceedings of Machine Learning Research, Proceedings of the 34th International Conference on Machine Learning, Sydney, NSW, Australia, 6–11 August 2017; JMLR.org: Sydney, Australia, 2017; Volume 70, pp. 1263–1272. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30, 5998–6008. [Google Scholar]
- Eguchi, R.R.; Choe, C.A.; Huang, P.-S. Ig-VAE: Generative modeling of protein structure by direct 3D coordinate generation. PLOS Comput. Biol. 2022, 18, e1010271. [Google Scholar] [CrossRef]
- Anand, N.; Huang, P. Generative modeling for protein structures. In Advances in Neural Information Processing Systems; Bengio, S., Wallach, H., Larochelle, H., Grauman, K., Cesa-Bianchi, N., Garnett, R., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2018. [Google Scholar]
- Zhang, L.; Han, J.; Wang, H.; Car, R.; Weinan, E. Deep Potential Molecular Dynamics: A Scalable Model with the Accuracy of Quantum Mechanics. Phys. Rev. Lett. 2018, 120, 143001. [Google Scholar] [CrossRef] [Green Version]
- Mead, A. Review of the Development of Multidimensional Scaling Methods. J. R. Stat. Soc. 1992, 41, 27–39. [Google Scholar] [CrossRef]
- Smith, J.S.; Isayev, O.; Roitberg, A.E. ANI-1: An extensible neural network potential with DFT accuracy at force field computational cost. Chem. Sci. 2017, 8, 3192–3203. [Google Scholar] [CrossRef] [Green Version]
- Behler, J. Constructing high-dimensional neural network potentials: A tutorial review. Int. J. Quantum Chem. 2015, 115, 1032–1050. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, H.; Chen, W.; Zeng, J.; Zhang, L.; Wang, H.; Weinan, E. DP-GEN: A concurrent learning platform for the generation of reliable deep learning based potential energy models. Comput. Phys. Commun. 2020, 253, 107206. [Google Scholar] [CrossRef] [Green Version]
- Xu, M.; Zhu, T.; Zhang, J.Z.H. Automated Construction of Neural Network Potential Energy Surface: The Enhanced Self-Organizing Incremental Neural Network Deep Potential Method. J. Chem. Inf. Model. 2021, 61, 5425–5437. [Google Scholar] [CrossRef]
- Smith, J.S.; Nebgen, B.; Lubbers, N.; Isayev, O.; Roitberg, A.E. Less is more: Sampling chemical space with active learning. J. Chem. Phys. 2018, 148, 241733. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gao, X.; Ramezanghorbani, F.; Isayev, O.; Smith, J.S.; Roitberg, A.E. TorchANI: A Free and Open Source PyTorch-Based Deep Learning Implementation of the ANI Neural Network Potentials. J. Chem. Inf. Model 2020, 60, 3408–3415. [Google Scholar] [CrossRef] [PubMed]
- Johnson, D.B. A note on Dijkstra’s shortest path algorithm. J. ACM (JACM) 1973, 20, 385–388. [Google Scholar] [CrossRef]
- Halgren, T.A. Merck molecular force field. I. Basis, form, scope, parameterization, and performance of MMFF94. J. Comput. Chem. 1996, 17, 490–519. [Google Scholar] [CrossRef]
- Schrier, J. Can One Hear the Shape of a Molecule (from its Coulomb Matrix Eigenvalues)? J. Chem. Inf. Model. 2020, 60, 3804–3811. [Google Scholar] [CrossRef]
- Song, Y.; Zheng, S.; Niu, Z.; Fu, Z.-H.; Lu, Y.; Yang, Y. Communicative Representation Learning on Attributed Molecular Graphs. In International Joint Conference on Artificial Intelligence; Bessiere, Proceedings of the Twenty-Ninth International Joint Conference on Artificial Intelligence, Yokohama, Japan, 7–15 January 2021; International Joint Conferences on Artificial Intelligence Organization: Pasadena, CA, USA, 2020. [Google Scholar]
- Ester, M.; Kriegel, H.-P.; Sander, J.; Xu, X. A density-based algorithm for discovering clusters in large spatial databases with noise. In Proceedings of the Second International Conference on Knowledge Discovery and Data Mining, München, Germany, 2–4 August 1996; AAAI Press: Chicago, IL, USA, 1996; pp. 226–231. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Feng, Z.; Chen, L.; Maddula, H.; Akcan, O.; Oughtred, R.; Berman, H.; Westbrook, J. Ligand Depot: A data warehouse for ligands bound to macromolecules. Bioinformatics 2004, 20, 2153–2155. [Google Scholar] [CrossRef] [Green Version]
- Berman, H.; Henrick, K.; Nakamura, H. Announcing the worldwide Protein Data Bank. Nat. Struct. Mol. Biol. 2003, 10, 980. [Google Scholar] [CrossRef]
- Case, D.A.; Brozell, S.R.; Cerutti, D.S.; Cheatham, T.E., III; Cruzeiro, V.W.D.; Darden, T.A.; Duke, R.E.; Ghoreishi, D.; Gilson, M.K.; Gohlke, H.; et al. AMBER 2018; University of California: San Francisco, CA, USA, 2018. [Google Scholar]
- Frisch, M.; Trucks, G.; Schlegel, H.; Scuseria, G.; Robb, M.; Cheeseman, J.; Scalmani, G.; Barone, V.; Petersson, G.; Nakatsuji, H. Gaussian 16; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Loshchilov, I.; Hutter, F. Decoupled weight decay regularization. arXiv 2017, arXiv:1711.05101. [Google Scholar]
- Amari, S.-I. Backpropagation and stochastic gradient descent method. Neurocomputing 1993, 5, 185–196. [Google Scholar] [CrossRef]
- Maier, J.A.; Martinez, C.; Kasavajhala, K.; Wickstrom, L.; Hauser, K.E.; Simmerling, C. ff14SB: Improving the accuracy of protein side chain and backbone parameters from ff99SB. J. Chem. Theory Comput. 2015, 11, 3696–3713. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Landrum, G. RDKit: A Software Suite for Cheminformatics, Computational Chemistry and Predictive Modeling. 2013. Available online: http://www.rdkit.org/RDKit_Overview.pdf (accessed on 23 December 2022).
- Eastman, P.; Swails, J.; Chodera, J.D.; McGibbon, R.T.; Zhao, Y.; Beauchamp, K.A.; Wang, L.-P.; Simmonett, A.C.; Harrigan, M.P.; Stern, C.D.; et al. OpenMM 7: Rapid development of high performance algorithms for molecular dynamics. PLOS Comput. Biol. 2017, 13, e1005659. [Google Scholar] [CrossRef] [PubMed]










| System | Structures | No of Atoms | % of Noise | RMSD (Å) | Torsion RMSD (°) | ||||
|---|---|---|---|---|---|---|---|---|---|
| GIE-RC | GIE-RC | ||||||||
| PLP |  | 24 | 0.0 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 2.5 | 0.11 | 0.43 | 0.63 | 0.96 | 4.13 | 48.91 | |||
| 5.0 | 0.19 | 1.11 | 1.15 | 2.09 | 9.55 | 71.96 | |||
| 10.0 | 0.47 | 2.14 | 2.31 | 3.67 | 16.72 | 84.03 | |||
| ATP |  | 43 | 0.0 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 2.5 | 0.21 | 0.87 | 1.09 | 0.93 | 4.78 | 78.98 | |||
| 5.0 | 0.48 | 2.41 | 2.14 | 2.1 | 8.92 | 94.07 | |||
| 10.0 | 1.20 | 4.27 | 4.23 | 4.49 | 18.43 | 99.13 | |||
| 1LE1 |  | 145 | 0.0 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 2.5 | 0.89 | 5.08 | 1.47 | 1.08 | 5.51 | 81.71 | |||
| 5.0 | 1.45 | 7.18 | 2.94 | 2.16 | 10.48 | 98.3 | |||
| 10.0 | 2.92 | 14.84 | 5.86 | 3.76 | 21.57 | 105.49 | |||
| 2I9M |  | 150 | 0.0 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 2.5 | 1.12 | 6.43 | 1.79 | 1.19 | 5.18 | 87.48 | |||
| 5.0 | 2.73 | 13.56 | 3.42 | 2.34 | 10.79 | 102.92 | |||
| 10.0 | 5.20 | 22.06 | 6.97 | 4.51 | 21.14 | 107.92 | |||
| System | Dataset | Graph-AE | Naive AE | ||
|---|---|---|---|---|---|
| RMSD (Å) | Torsion RMSD (°) | RMSD (Å) | Torsion RMSD (°) | ||
| PLP | Training set | 0.22 | 6.68 | 0.22 | 5.73 |
| Test set | 0.39 | 15.80 | 0.59 | 18.46 | |
| ATP | Training set | 0.59 | 10.46 | 0.30 | 10.74 |
| Test set | 0.9 | 17.69 | 0.68 | 15.23 | |
| 2I9M | Training set | 0.85 | 2.35 | 4.25 | 38.59 |
| Test set | 0.91 | 2.40 | 6.42 | 46.74 | |
| 1LE1 | Training set | 0.74 | 2.30 | 3.80 | 38.83 |
| Test set | 0.76 | 2.31 | 5.05 | 40.07 | |
| Ligand Depot | Training set | 0.69 | 9.46 | / | / |
| Test set | 0.78 | 10.18 | / | / | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, M.; Huang, W.; Xu, M.; Lei, J.; Chen, H. 3D Conformational Generative Models for Biological Structures Using Graph Information-Embedded Relative Coordinates. Molecules 2023, 28, 321. https://doi.org/10.3390/molecules28010321
Xu M, Huang W, Xu M, Lei J, Chen H. 3D Conformational Generative Models for Biological Structures Using Graph Information-Embedded Relative Coordinates. Molecules. 2023; 28(1):321. https://doi.org/10.3390/molecules28010321
Chicago/Turabian StyleXu, Mingyuan, Weifeng Huang, Min Xu, Jinping Lei, and Hongming Chen. 2023. "3D Conformational Generative Models for Biological Structures Using Graph Information-Embedded Relative Coordinates" Molecules 28, no. 1: 321. https://doi.org/10.3390/molecules28010321
APA StyleXu, M., Huang, W., Xu, M., Lei, J., & Chen, H. (2023). 3D Conformational Generative Models for Biological Structures Using Graph Information-Embedded Relative Coordinates. Molecules, 28(1), 321. https://doi.org/10.3390/molecules28010321