Possible Effects of Changes in Carbonate Concentration and River Flow Rate on Photochemical Reactions in Temperate Aquatic Environments
Abstract
:1. Introduction
2. Results and Discussion
2.1. Changes in pH and Total Carbonates
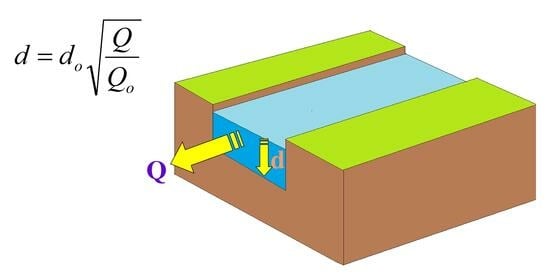
2.2. Photochemical Implications of Flow Changes in Rivers
3. Methods
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Sample Availability
References
- Sanchez, W.; Egea, E. Health and environmental risks associated with emerging pollutants and novel green processes. Environ. Sci. Pollut. Res. Int. 2018, 25, 6085–6086. [Google Scholar] [CrossRef]
- Turner, S.W.D.; Rice, J.S.; Nelson, K.D.; Vernon, C.R.; McManamay, R.; Dickson, K.; Marston, L. Comparison of potential drinking water source contamination across one hundred U.S. cities. Nat. Commun. 2021, 12, 7254. [Google Scholar] [CrossRef]
- Richardson, S.D.; Ternes, T.A. Water analysis: Emerging contaminants and current issues. Anal. Chem. 2022, 94, 382–416. [Google Scholar] [CrossRef] [PubMed]
- Lau, S.S.; Bokenkamp, K.; Tecza, A.; Wagner, E.D.; Plewa, M.J.; Mitch, W.A. Toxicological assessment of potable reuse and conventional drinking waters. Nat. Sustain. 2023, 6, 39–46. [Google Scholar] [CrossRef]
- Riva, F.; Zuccato, E.; Pacciani, C.; Colombo, A.; Castiglioni, S. A multi-residue analytical method for extraction and analysis of pharmaceuticals and other selected emerging contaminants in sewage sludge. Anal. Methods 2021, 13, 526–535. [Google Scholar] [CrossRef] [PubMed]
- Arsene, C.; Bejan, I.G.; Roman, C.; Olariu, R.I.; Minella, M.; Passananti, M.; Carena, L.; Vione, D. Evaluation of the environmental fate of a semivolatile transformation product of ibuprofen based on a simple two-media fate model. Environ. Sci. Technol. 2022, 56, 15650–15660. [Google Scholar] [CrossRef]
- Maldonado-Torres, S.; Gurung, R.; Rijal, H.; Chan, A.; Acharya, S.; Rogelj, S.; Piyasena, M.; Rubasinghege, G. Fate, transformation, and toxicological impacts of pharmaceutical and personal care products in surface waters. Environ. Health Insights 2018, 12, 1178630218795836. [Google Scholar] [CrossRef]
- Vione, D.; Minella, M.; Maurino, V.; Minero, C. Indirect photochemistry in sunlit surface waters: Photoinduced production of reactive transient species. Chem. Eur. J. 2014, 20, 10590–10606. [Google Scholar] [CrossRef]
- Guo, Z.; Kodikara, D.; Albi, L.S.; Hatano, Y.; Chen, G.; Yoshimura, C.; Wang, J. Photodegradation of organic micropollutants in aquatic environment: Importance, factors and processes. Water Res. 2023, 231, 118236. [Google Scholar] [CrossRef]
- Mc Neill, K.; Canonica, S. Triplet state dissolved organic matter in aquatic photochemistry: Reaction mechanisms, substrate scope, and photophysical properties. Environ. Sci.-Process Impacts 2016, 18, 1381–1399. [Google Scholar] [CrossRef]
- Vione, D.; Scozzaro, A. Photochemistry of surface fresh waters in the framework of climate change. Environ. Sci. Technol. 2019, 53, 7945–7963. [Google Scholar] [CrossRef] [PubMed]
- Ossola, R.; Jönsson, O.M.; Moor, K.; McNeill, K. Singlet oxygen quantum yields in environmental waters. Chem. Rev. 2021, 121, 4100–4146. [Google Scholar] [CrossRef] [PubMed]
- Kostić, S.; Stojković, M.; Prohaska, S.; Vasović, N. Modeling of river flow rate as a function of rainfall and temperature using response surface methodology based on historical time series. J. Hydroinform. 2016, 18, 651–665. [Google Scholar] [CrossRef]
- Worrall, F.; Howden, N.J.K.; Burt, T.P. A method of estimating in-stream residence time of water in rivers. J. Hydrol. 2014, 512, 274–284. [Google Scholar] [CrossRef]
- Adrian, R.; O’Reilly, C.M.; Zagarese, H.; Baines, S.B.; Hessen, D.O.; Keller, W.; Livingstone, D.M.; Sommaruga, R.; Straile, D.; Van Donk, E.; et al. Lakes as sentinels of climate change. Limnol. Oceanogr. 2009, 54, 2283–2297. [Google Scholar] [CrossRef] [PubMed]
- Williamson, C.E.; Overholt, E.P.; Pilla, R.M.; Leach, T.H.; Brentrup, J.A.; Knoll, L.B.; Mette, E.M.; Moeller, R.E. Ecological consequences of long-term browning in lakes. Sci. Rep. 2016, 5, 18666. [Google Scholar] [CrossRef]
- Klante, C.; Larson, M.; Persson, K.M. Brownification in Lake Bolmen, Sweden, and its relationship to natural and human-induced changes. J. Hydrol. Reg. Studies 2021, 36, 100863. [Google Scholar] [CrossRef]
- Kritzberg, E.S.; Hasselquist, E.M.; Škerlep, M.; Löfgren, S.; Olsson, O.; Stadmark, J.; Valinia, S.; Hansson, L.A.; Laudon, H. Browning of freshwaters: Consequences to ecosystem services, underlying drivers, and potential mitigation measures. Ambio 2020, 49, 375–390. [Google Scholar] [CrossRef]
- Schindler, D.W. Widespread effects of climatic warming on freshwater ecosystems in North America. Hydrol. Proc. 1997, 11, 1043–1067. [Google Scholar] [CrossRef]
- Tuel, A.; Eltahir, E.A.B. Why is the Mediterranean a climate change hot spot? J. Clim. 2020, 33, 5829–5843. [Google Scholar] [CrossRef]
- Vione, D. A critical view of the application of the APEX software (Aqueous Photochemistry of Environmentally-occurring Xenobiotics) to predict photoreaction kinetics in surface freshwaters. Molecules 2020, 25, 9. [Google Scholar] [CrossRef] [PubMed]
- Tixier, C.; Singer, H.P.; Oellers, S.; Mueller, S.R. Occurrence and fate of carbamazepine, clofibric acid, diclofenac, ibuprofen, ketoprofen, and naproxen in surface waters. Environ. Sci. Technol. 2003, 37, 1061–1068. [Google Scholar] [CrossRef] [PubMed]
- Canonica, S.; Kohn, T.; Mac, M.; Real, F.J.; Wirz, J.; Von Gunten, U. Photosensitizer method to determine rate constants for the reaction of carbonate radical with organic compounds. Environ. Sci. Technol. 2005, 39, 9182–9188. [Google Scholar] [CrossRef] [PubMed]
- Yan, S.; Liu, Y.; Lian, L.; Li, R.; Ma, J.; Zhou, H.; Song, W. Photochemical formation of carbonate radical and its reaction with dissolved organic matters. Water Res. 2019, 161, 288–296. [Google Scholar] [CrossRef] [PubMed]
- Buxton, G.V.; Greenstock, C.L.; Helman, P.W.; Ross, A.B. Critical review of rate constants for reactions of hydrated electrons, hydrogen atoms and hydroxyl radicals (•OH/•O−) in aqueous solution. J. Phys. Chem. Ref. Data 1988, 17, 513–886. [Google Scholar] [CrossRef]
- Rogora, M.; Mosello, R.; Arisci, S.; Brizzio, M.C.; Barbieri, A.; Balestrini, R.; Waldner, P.; Schmitt, M.; Sthäli, M.; Thimonier, A.; et al. An overview of atmospheric deposition chemistry over the Alps: Present status and long-term trends. Hydrobiologia 2006, 562, 17–40. [Google Scholar] [CrossRef]
- Carena, L.; Vione, D.; Minella, M.; Canonica, S.; Schönenberger, U. Inhibition by phenolic antioxidants of the degradation of aromatic amines and sulfadiazine by the carbonate radical (CO3•−). Water Res. 2021, 209, 117867. [Google Scholar] [CrossRef]
- Zobrist, J.; Schoenenberger, U.; Figura, S.; Hug, S.J. Long-term trends in Swiss rivers sampled continuously over 39 years reflect changes in geochemical processes and pollution. Environ. Sci. Pollut. Res. Int. 2018, 25, 16788–16809. [Google Scholar] [CrossRef]
- Vione, D.; Encinas, A.; Fabbri, D.; Calza, P. A model assessment of the potential of river water to induce the photochemical attenuation of pharmaceuticals downstream of a wastewater treatment plant (Guadiana River, Badajoz, Spain). Chemosphere 2018, 198, 473–481. [Google Scholar] [CrossRef]
- Bintou, A.T.; Bianco, A.; Mailhot, G.; Brigante, M. A new insight into ethoxyquin fate in surface waters: Stability, direct and indirect photochemical behaviour and the identification of main products. J. Photochem. Photobiol. A Chem. 2015, 311, 118–126. [Google Scholar] [CrossRef]
- Silva, M.P.; Mostafa, S.; McKay, G.; Rosario-Ortiz, F.L.; Teixeira, A.C.S.C. Photochemical fate of amicarbazone in aqueous media: Laboratory measurement and simulations. Environ. Eng. Sci. 2015, 32, 730–740. [Google Scholar] [CrossRef]
- Lastre-Acosta, A.M.; Barberato, B.; Parizi, M.P.S.; Teixeira, A.C.S.C. Direct and indirect photolysis of the antibiotic enoxacin: Kinetics of oxidation by reactive photo-induced species and simulations. Environ. Sci. Pollut. Res. 2019, 26, 4337–4347. [Google Scholar] [CrossRef] [PubMed]
- Parizi, M.P.S.; Acosta, A.M.L.; Ishiki, H.M.; Rossi, R.C.; Mafra, R.C.; Teixeira, A.C.S.C. Environmental photochemical fate and UVC degradation of sodium levothyroxine in aqueous medium. Environ. Sci. Pollut. Res. 2019, 26, 4393–4403. [Google Scholar] [CrossRef] [PubMed]
- Jane, S.F.; Hansen, G.J.A.; Kraemer, B.M.; Leavitt, P.R.; Mincer, J.L.; North, R.L.; Pilla, R.M.; Stetler, J.T.; Williamson, C.E.; Woolway, R.I.; et al. Widespread deoxygenation of temperate lakes. Nature 2021, 594, 66–70. [Google Scholar] [CrossRef] [PubMed]
- Zhi, W.; Klingler, C.; Liu, J.; Li, L. Widespread deoxygenation in warming rivers. Nat. Clim. Chang. 2023, 13, 1105–1113. [Google Scholar] [CrossRef]








| Φdp, mol Ein−1 | , M−1 s−1 | , M−1 s−1 | , M−1 s−1 | , M−1 s−1 | |
|---|---|---|---|---|---|
| APAP | 4.6 × 10−2 | 1.9 × 109 | 3.8 × 108 | 1.6 × 109 | 3.7 × 107 |
| DIC | 9.4 × 10−2 | 9.3 × 109 | Low | 6.4 × 108 | 1.3 × 107 |
| NAP | 1.0 × 10−2 | 8 × 109 | Low | 7.5 × 108 | 1.1 × 105 |
| BP4, acidic | 3.2 × 10−5 | 1.9 × 1010 | Low | Low | Low |
| BP4, basic | 7.0 × 10−5 | 8.5 × 109 | Low | Low | Low |
| TRIC, acidic | 0.3 | 5.4 × 109 | Low | 3.1 × 109 | 3 × 106 |
| TRIC, basic | 0.3 | 1 × 1010 | Low | 4.3 × 109 | 1.1 × 108 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vione, D.; Saglia, F.; Pelazza, C. Possible Effects of Changes in Carbonate Concentration and River Flow Rate on Photochemical Reactions in Temperate Aquatic Environments. Molecules 2023, 28, 7072. https://doi.org/10.3390/molecules28207072
Vione D, Saglia F, Pelazza C. Possible Effects of Changes in Carbonate Concentration and River Flow Rate on Photochemical Reactions in Temperate Aquatic Environments. Molecules. 2023; 28(20):7072. https://doi.org/10.3390/molecules28207072
Chicago/Turabian StyleVione, Davide, Federica Saglia, and Carola Pelazza. 2023. "Possible Effects of Changes in Carbonate Concentration and River Flow Rate on Photochemical Reactions in Temperate Aquatic Environments" Molecules 28, no. 20: 7072. https://doi.org/10.3390/molecules28207072
APA StyleVione, D., Saglia, F., & Pelazza, C. (2023). Possible Effects of Changes in Carbonate Concentration and River Flow Rate on Photochemical Reactions in Temperate Aquatic Environments. Molecules, 28(20), 7072. https://doi.org/10.3390/molecules28207072