Errors in the Calculation of 27Al Nuclear Magnetic Resonance Chemical Shifts
Abstract
:1. Introduction
2. Results and Discussion
2.1. Chemical Shielding Constants
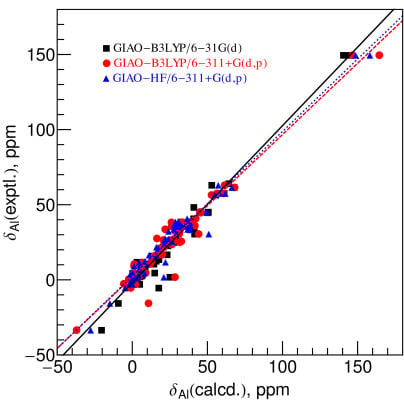
2.2. Comparison between Experimental and Calculated Chemical Shifts
2.3. Geometry Optimization
2.4. Solvent Effect
3. Computational Details
4. Conclusions
Acknowledgments
- Conflict of InterestThe authors declare no conflict of interest.
References
- Lewis, T. Environmental Chemistry and Toxicology of Aluminium, 1st ed; CRC Press: Boca Raton, FL, USA, 1989. [Google Scholar]
- Sposito, G. The Environmental Chemistry of Aluminum, 2nd ed; CRC Press: Boca Raton, FL, USA, 1995. [Google Scholar]
- Wang, X.L.; Zou, G.; Bi, S. Advances in determination of aluminum in environmental and biological materials by 27Al nuclear magnetic resonance spectroscopy. Chin. J. Inorg. Chem 2000, 16, 548–560. [Google Scholar]
- Tossell, J.A. The effects of hydrolysis and oligomerization upon the NMR shieldings of Be+2 and Al+3 species in aqueous solution. J. Magn. Reson 1998, 135, 203–207. [Google Scholar]
- Ditchfield, R. Self-consistent perturbation theory of diamagnetism. Mol. Phys 1974, 27, 789–807. [Google Scholar]
- Wolinski, K.; Hinton, J.F.; Pulay, P. Efficient implementation of the gauge-independent atomic orbital method for NMR chemical shift calculations. J. Am. Chem. Soc 1990, 112, 8251–8260. [Google Scholar]
- Amini, S.K.; Tafazzoli, M. DFT calculations as a powerful technique to probe the crystal structure of Al(acac)3. Magn. Reson. Chem 2008, 46, 1045–1050. [Google Scholar]
- Schurko, R.W.; Wasylishen, R.E.; Foerster, H. Characterization of anisotropic aluminum magnetic shielding tensors. Distorted octahedral complexes and linear molecules. J. Phys. Chem. A 1998, 102, 9750–9760. [Google Scholar]
- Mirzaei, M.; Mirzaei, M. Aluminum phosphide nanotubes: Density functional calculations of aluminum-27 and phosphorus-31 chemical shielding parameters. J. Mol. Struct 2010, 951, 69–71. [Google Scholar]
- Bodaghi, A.; Mirzaei, M.; Seif, A.; Giahi, M. A computational NMR study on zigzag aluminum nitride nanotubes. Physica E 2008, 41, 209–212. [Google Scholar]
- Charpentier, T. The PAW/GIPAW approach for computing NMR parameters: A new dimension added to NMR study of solids. Solid State Nucl. Magn. Reson 2011, 40, 1–20. [Google Scholar]
- Pickard, C.J.; Mauri, F. All-electron magnetic response with pseudopotentials: NMR chemical shifts. Phys. Rev. B 2001, 63, 245101. [Google Scholar]
- Pedone, A.; Gambuzzi, E.; Malavasi, G.; Menziani, M.C. First-principles simulations of the 27Al and 17O solid-state NMR spectra of the CaAl2Si3O10 glass. Theor. Chem. Acc 2012, 131, 1147. [Google Scholar]
- Choi, M.; Matsunaga, K.; Oba, F.; Tanaka, I. 27Al NMR chemical shifts in oxide crystals: A first-principles study. J. Phys. Chem. C 2009, 113, 3869–3873. [Google Scholar]
- Mulder, F.A.; Filatov, M. NMR chemical shift data and ab initio shielding calculations: Emerging tools for protein structure determination. Chem. Soc. Rev 2010, 39, 578–590. [Google Scholar]
- Jensen, F. Basis set convergence of nuclear magnetic shielding constants calculated by density functional methods. J. Chem. Theory Comput 2008, 4, 719–727. [Google Scholar]
- Kubicki, J.D.; Sykes, D.; Apitz, S.E. Ab initio calculation of aqueous aluminum and aluminum-carboxylate complex energetics and 27Al NMR chemical shifts. J. Phys. Chem. A 1999, 103, 903–915. [Google Scholar]
- Qian, Z.; Feng, H.; He, L.; Yang, W.; Bi, S. Assessment of the accuracy of theoretical methods for calculating 27Al nuclear magnetic resonance shielding tensors of aquated aluminum species. J. Phys. Chem. A 2009, 113, 5138–5143. [Google Scholar]
- Stack, A.G.; Rustad, J.R.; Casey, W.H. Modeling water exchange on an aluminum polyoxocation. J. Phys. Chem. B 2005, 109, 23771–23775. [Google Scholar]
- Malone, S.A.; Cooper, P.; Heath, S.L. Synthesis and structure of a new aluminium citrate trimer from aqueous solution at very low pH. Dalton Trans. 2003, 4572–4573. [Google Scholar]
- Karlsson, M.; Boström, D.; Öhman, L. Equilibrium and structural studies of silicon(IV) and aluminium(III) in aqueous solution. 33. The Al(methylmalonate)2(H2O)2− complex crystallised as a double salt with Al(H2O)6 (3+) and Cl−. Acta Chem. Scand 1998, 52, 995–999. [Google Scholar]
- Bataille, T. Hemi(piperazinediium) hexaaquaaluminium(III) bis(sulfate) tetrahydrate: A new double aluminium sulfate salt. Acta Cryst. C 2003, 59, m459–m461. [Google Scholar]
- Dalrymple, S.A.; Parvez, M.; Shimizu, G.K. Intra- and intermolecular second-sphere coordination chemistry: Formation of capsules, half-capsules, and extended structures with hexaaquo- and hexaamminemetal ions. Inorg. Chem 2002, 41, 6986–6996. [Google Scholar]
- Shen, R.; Pan, X.; Wang, H.; Yao, L.; Wu, J.; Tang, N. Selective colorimetric and fluorescent detection of HSO4− with sodium(i), magnesium(ii) and aluminium(iii) xanthone-crown ether complexes. Dalton Trans. 2008, 3574–3581. [Google Scholar]
- Mainicheva, E.; Gerasko, O.; Sheludyakova, L.; Naumov, D.; Naumova, M.; Fedin, V. Synthesis and crystal structures of supramolecular compounds of polynuclear aluminum(III) aqua hydroxo complexes with cucurbit[6]uril. Russ. Chem. Bull 2006, 55, 267–275. [Google Scholar]
- Casey, W.H.; Olmstead, M.M.; Phillips, B.L. A new aluminum hydroxide octamer, [Al8(OH)14(H2O)18](SO4)5·16H2O. Inorg. Chem 2005, 44, 4888–4890. [Google Scholar]
- Gatlin, J.T.; Mensinger, Z.L.; Zakharov, L.N.; MacInnes, D.; Johnson, D.W. Facile synthesis of the tridecameric Al13 nanocluster Al13(μ3-OH)6(μ2-OH)18(H2O)24(NO3)15. Inorg. Chem 2008, 47, 1267–1269. [Google Scholar]
- Plutecka, A.; Rychlewska, U. A three-dimensional AlIII/NaI metal-organic framework resulting from dimethylformamide hydrolysis. Acta Cryst. C 2009, 65, m75–m77. [Google Scholar]
- Bekaert, A.; Barberan, O.; Kaloun, E.B.; Rabhi, C.; Danan, A.; Brion, J.D.; Lemoine, P.; Viossat, B. Crystal structure of hexakis (N,N-dimethylformamide-O) aluminium (III) tris (tribromide), Al [(CH3)2N(CH)O]6(Br3)3. Z. Kristallogr 2002, 217, 128–130. [Google Scholar]
- Suzuki, H.; Ishiguro, S. N,N-Dimethylformamide complex of aluminium(III) perchlorate. Acta Cryst. C 1998, 54, 586–588. [Google Scholar]
- Suzuki, H.; Ishiguro, S. N,N-Dimethyl-acetamide complex of aluminium(III) perchlorate. Acta Cryst. E 2006, 62, m576–m578. [Google Scholar]
- Riesen, H.; Rae, A.D. Revisiting the crystal structure and thermal properties of NaMgAl(oxalate)3.9H2O/Cr(iii): An extraordinary spectral hole-burning material. Dalton Trans. 2008, 4717–4722. [Google Scholar]
- Taylor, D. Crystal structures of potassium tris(oxalato) chromate(III) and potassium tris(oxalato) aluminate(III) trihydrate-reinvestigation. Aust. J. Chem 1978, 31, 1455–1462. [Google Scholar]
- Bulc, N.; Golic, L.; Siftar, J. Structure of ammonium tris(oxalato)gallate(III) trihydrate, (I) (NH4)3[Ga(C2O4)3].3H2O, and ammonium tris(oxalato)aluminate(III) trihydrate, (II) (NH4)3[Al(C2O4)3].3H2O. Acta Cryst. C 1984, 40, 1829–1831. [Google Scholar]
- Chohan, S.; Pritchard, R.G. Tripotassium tris(oxalato-κ2O,O′)-aluminate bis(hydrogen peroxide) hydrate, the first example of a cyclic hydrogen-bonded H2O2 dimer. Acta Cryst. C 2003, 59, m187–m189. [Google Scholar]
- Pellaux, R.; Decurtins, S.; Schmalle, H.W. Three anionic polymeric networks: Sodium(I)-ruthenium(III), sodium(I)-rhodium(III) and sodium(I)-aluminium(III) μ-oxalato complexes with tris(2,2′-bipyridine)ruthenium(II) cations. Acta Cryst. C 1999, 55, 1075–1079. [Google Scholar]
- Martin, L.; Turner, S.S.; Day, P.; Guionneau, P.; Howard, J.A.; Hibbs, D.E.; Light, M.E.; Hursthouse, M.B.; Uruichi, M.; Yakushi, K. Crystal chemistry and physical properties of superconducting and semiconducting charge transfer salts of the type (BEDT-TTF)4[AIMIII(C2O4)3]·PhCN (AI = H3O, NH4, K; MIII = Cr, Fe, Co, Al; BEDT-TTF = Bis(ethylenedithio)tetrathiafulvalene). Inorg. Chem 2001, 40, 1363–1371. [Google Scholar]
- Bulc, N.; Golic, L.; Siftar, J. Structure of sodium trisoxalatoaluminate(III) pentahydrate and sodium trisoxalatochromate(III) pentahydrate, Na3[Al(C2O4)3]·5H2O and Na3[Cr(C2O4)3]·5H2O. Vestn. Slov. Kem. Drus Bull. Slov. Chem. Soc 1982, 29, 211–215. [Google Scholar]
- Golič, L.; Leban, I.; Bulc, N. The structure of sodium bis(tetraethylammonium) tris(oxalato)aluminate(III) monohydrate. Acta Cryst. C 1989, 45, 44–46. [Google Scholar]
- Tapparo, A.; Heath, S.L.; Jordan, P.A.; Moore, G.R.; Powell, A.K. Crystal structure and solution-state study of K[Al(mal)2(H2O)2]·2H2O (H2mal = malonic acid). J. Chem. Soc. Dalton Trans. 1996, 1601–1606. [Google Scholar]
- Diaz-Acosta, I.; Baker, J.; Cordes, W.; Pulay, P. Calculated and experimental geometries and infrared spectra of metal tris-acetylacetonates: Vibrational spectroscopy as a probe of molecular structure for ionic complexes. Part I. J. Phys. Chem. A 2001, 105, 238–244. [Google Scholar]
- Von Chrzanowski, L.S.; Lutz, M.; Spek, A.L. alpha-Tris(2,4-pentanedionato-κ2O,O′) aluminum(III) at 240, 210, 180, 150 and 110 K: A new delta phase at 110 K. Acta Cryst. Sect. C 2007, 63, m129. [Google Scholar]
- Thurston, J.H.; Trahan, D.; Ould-Ely, T.; Whitmire, K.H. Toward a general strategy for the synthesis of heterobimetallic coordination complexes for use as precursors to metal oxide materials: synthesis, characterization, and thermal decomposition of Bi2(Hsal)6·M(Acac)3 (M = Al, Co, V, Fe, Cr). Inorg. Chem 2004, 43, 3299–3305. [Google Scholar]
- Alekseev, A.; Gromilov, S.; Baidina, I.; Stabnikov, P.; Prokuda, O. Synthesis of bimetallic complexes based on acetylacetonates of aluminum and ferrum. Crystalline structure Al0.9Fe0.1(acac)3. J. Struct. Chem 2006, 47, 318–325. [Google Scholar]
- Le, Q.T.H.; Umetani, S.; Matsui, M. Ion-size recognition of Group 13 metals (Al3+, In3+) with modified-diketones. J. Chem. Soc, Dalton Trans. 1997, 3835–3840. [Google Scholar]
- Zhang, C.; Yang, P.; Yang, Y.; Huang, X.; Yang, X.; Wu, B. High-yield synthesis of 1,3-dimesityl-propane-1,3-dione: Isolation of its aluminum complex as a stable intermediate. Synth. Commun 2008, 38, 2349–2356. [Google Scholar]
- Hori, A.; Shinohe, A.; Takatani, S.; Miyamoto, T.K. Synthesis and crystal structures of fluorinated β-diketonate metal (Al3+, Co2+, Ni2+ and Cu2+) complexes. Bull. Chem. Soc. Jpn 2009, 82, 96–98. [Google Scholar]
- Neelgund, G.M.; Shivashankar, S.A.; Narasimhamurthy, T.; Ng, S.W. Tris(methyl 3-oxobutanoato-κ2O,O′)aluminium(III). Acta Cryst. E 2009, 65, m1681. [Google Scholar]
- Dharmaprakash, M.S.; Thamotharan, S.; Neelgundc, G.M.; Shivashankarc, S.A. Tris(tert-butyl 3-oxobutanoato-κ2O1,O3)-aluminium (III) at 153 K. Acta Cryst. E 2006, 62, m434–m436. [Google Scholar]
- Vreshch, V.D.; Lysenko, A.B.; Chernega, A.N.; Howard, J.A.; Krautscheid, H.; Sieler, J.; Domasevitch, K.V. Extended coordination frameworks incorporating heterobimetallic squares. Dalton Trans. 2004, 2899–2903. [Google Scholar]
- Lutz, T.G.; Clevette, D.J.; Rettig, S.J.; Orvig, C. Metal chelation with natural products: Isomaltol complexes of aluminum, gallium, and indium. Inorg. Chem 1989, 28, 715–719. [Google Scholar]
- Yu, P.; Phillips, B.L.; Olmstead, M.M.; Casey, W.H. Rates of solvent exchange in aqueous aluminium(iii)-maltolate complexes. J. Chem. Soc, Dalton Trans. 2002, 2119–2125. [Google Scholar]
- Odoko, M.; Yamamoto, K.; Hosen, M.; Okabe, N. fac-Tris(2-ethyl-4-oxo-4H-pyran-3-olato-κ2O3,O4) iron (III) and its aluminium (III) analog. Acta Cryst. C 2003, 59, m121–m123. [Google Scholar]
- Karpishin, T.B.; Stack, T.D.; Raymond, K.N. Octahedral versus trigonal prismatic geometry in a series of catechol macrobicyclic ligand-metal complexes. J. Am. Chem. Soc. 1993, 115, 182–192. [Google Scholar]
- Di Marco, V.B.; Bombi, G.; Tapparo, A.; Powell, A.K.; Anson, C.E. Complexation of aluminium(III) with 3-hydroxy-2(1H)-pyridinone. Solution state study and crystal structure of tris(3-hdroxy-2(1H)-pyridinonato)aluminium(III). J. Chem. Soc, Dalton Trans. 1999, 2427–2432. [Google Scholar]
- Nelson, W.O.; Rettig, S.J.; Orvig, C. Exoclathrate Al(C7H8NO2)3.12H2O. A facial geometry imposed by extensive hydrogen bonding with the ice I structure. J. Am. Chem. Soc 1987, 109, 4121–4123. [Google Scholar]
- Nelson, W.O.; Karpishin, T.B.; Rettig, S.J.; Orvig, C. Aluminum and gallium compounds of 3-hydroxy-4-pyridinones: synthesis, characterization, and crystallography of biologically active complexes with unusual hydrogen bonding. Inorg. Chem 1988, 27, 1045–1051. [Google Scholar]
- Simpson, L.; Rettig, S.J.; Trotter, J.; Orvig, C. 1-n-Propyl-and 1-n-butyl-3-hydroxy-2-methyl-4- pyridinone complexes of group 13 (IIIA) metal ions. Can. J. Chem 1991, 69, 893–900. [Google Scholar]
- Zhang, Z.; Rettig, S.J.; Orvig, C. Lipophilic coordination compounds: aluminum, gallium, and indium complexes of 1-aryl-3-hydroxy-2-methyl-4-pyridinones. Inorg. Chem 1991, 30, 509–515. [Google Scholar]
- Muetterties, E.L.; Guggenberger, L.J. Stereochemically nonrigid six-coordinate molecules. Crystal structure of tris(tropolonato)aluminum(III). J. Am. Chem. Soc 1972, 94, 8046–8055. [Google Scholar]
- Nomiya, K.; Yoshizawa, A.; Tsukagoshi, K.; Kasuga, N.C.; Hirakawa, S.; Watanabe, J. Synthesis and structural characterization of silver(I), aluminium(III) and cobalt(II) complexes with 4-isopropyltropolone (hinokitiol) showing noteworthy biological activities. Action of silver(I)-oxygen bonding complexes on the antimicrobial activities. J. Inorg. Biochem. 2004, 98, 46–60. [Google Scholar]
- Xu, J.; Parac, T.N.; Raymond, K.N. Meso myths: What drives assembly of helical versus meso-[M2L3] clusters? Angew. Chem. Int. Ed 1999, 38, 2878–2882. [Google Scholar]
- Wunderlich, C.H.; Bergerhoff, G. Crystal structure of di-μ-oxo-bis(bis(1,2- dihydroxyanthrachinonato)aluminium-(aquabis(dimethylformamide)calcium)), Al2O4(C14H6O4)4 Ca2(HCON (CH3)2)4(H2O)2,(alizarine complex). Z. Kristallogr 1993, 207, 185–188. [Google Scholar]
- Bergerhoff, G.; Wunderlich, C.H. Crystal structure of di-μ-oxo-bis(bis(1,2,4- trihydroxyanthrachinonato)aluminium-(aquabis(dimethylformamide)calcium)), Al2O4(C14H6O5)4 Ca2(HCON(CH3)2)4(H2O)2, (purpurine complex). Z. Kristallogr 2010, 207, 189–192. [Google Scholar]
- Venema, F.R.; van Koningsveld, H.; Peters, J.A.; van Bekkum, H. Co-operative hydrogen bonding with short O O distances in a binuclear Al-glycolate complex. J. Chem. Soc, Chem. Commun. 1990, 699–700. [Google Scholar]
- Van Koningsveld, H.; Venema, F.R. Structure of the hydrogen-bonded binuclear complex trisodium trihydrogen bis[tris(glycolato)aluminate(III)]. Acta Cryst. C 1991, 47, 289–292. [Google Scholar]
- Bombi, G.G.; Corain, B.; Sheikh-Osman, A.A.; Valle, G.C. The speciation of aluminum in aqueous solutions of aluminum carboxylates. Part I. X-ray molecular structure of Al[OC(O)CH(OH)CH3]3. Inorg. Chim. Acta 1990, 171, 79–83. [Google Scholar]
- Matzapetakis, M.; Raptopoulou, C.P.; Terzis, A.; Lakatos, A.; Kiss, T.; Salifoglou, A. Synthesis, structural characterization, and solution behavior of the first mononuclear, aqueous aluminum citrate complex. Inorg. Chem 1999, 38, 618–619. [Google Scholar]
- Matzapetakis, M.; Kourgiantakis, M.; Dakanali, M.; Raptopoulou, C.P.; Terzis, A.; Lakatos, A.; Kiss, T.; Banyai, I.; Iordanidis, L.; Mavromoustakos, T.; et al. Synthesis, pH-dependent structural characterization, and solution behavior of aqueous aluminum and gallium citrate complexes. Inorg. Chem 2001, 40, 1734–1744. [Google Scholar]
- Dakanali, M.; Raptopoulou, C.P.; Terzis, A.; Lakatos, A.; Banyai, I.; Kiss, T.; Salifoglou, A. A novel dinuclear species in the aqueous distribution of aluminum in the presence of citrate. Inorg. Chem 2003, 42, 252–254. [Google Scholar]
- Feng, T.L.; Gurian, P.L.; Healy, M.D.; Barron, A.R. Aluminum citrate: Isolation and structural characterization of a stable trinuclear complex. Inorg. Chem 1990, 29, 408–411. [Google Scholar]
- Keizer, T.S.; Scott, B.L.; Sauer, N.N.; McCleskey, T.M. Stable, soluble beryllium aluminum citrate complexes inspired by the emerald mineral structure. Angew. Chem. Int. Ed 2005, 44, 2403–2406. [Google Scholar]
- Happel, O.; Harms, K.; Seubert, A. Synthesis and structural characterization of two aluminium malate complexes. Z. Anorg. Allg. Chem 2007, 633, 1952–1958. [Google Scholar]
- Lakatos, A.; Bertani, R.; Kiss, T.; Venzo, A.; Casarin, M.; Benetollo, F.; Ganis, P.; Favretto, D. AlIII ion complexes of saccharic acid and mucic acid: A solution and solid-state study. Chem. Eur. J 2004, 10, 1281–1290. [Google Scholar]
- Klüfers, P.; Kramer, G.; Piotrowski, H.; Senker, J. Polyol-Metall-Komplexe, 43 [1]. Galactarato-Komplexe mit Aluminium und Kupfer (II). Z. Naturforsch. B 2002, 57, 1446–1453. [Google Scholar]
- Lewiński, J.; Zachara, J.; Grabska, E. Synthesis and molecular structure of (tBuOO)(tBuO)Al (μ-OtBu)2Al(mesal)2. The first structurally characterized (alkylperoxo)aluminum compound. J. Am. Chem. Soc 1996, 118, 6794–6795. [Google Scholar]
- Lewinski, J.; Zachara, J.; Gos, P.; Grabska, E.; Kopec, T.; Madura, I.; Marciniak, W.; Prowotorow, I. Reactivity of various four-coordinate aluminum alkyls towards dioxygen: Evidence for spatial requirements in insertion of an oxygen molecule into the Al–C bond. Chem. Eur. J 2000, 6, 3215–3227. [Google Scholar]
- Kessler, V.G.; Gohil, S.; Parola, S. Interaction of some divalent metal acetylacetonates with Al, Ti, Nb and Ta isopropoxides. Factors influencing the formation and stability of heterometallic alkoxide complexes. Dalton Trans. 2003, 544–550. [Google Scholar]
- Garbauskas, M.F.; Wengrovius, J.H. Structure of the aluminium alkoxide complex [Al(O-iPr)(3,5-heptanedione)2]2. Acta Cryst. C 1987, 43, 2441–2442. [Google Scholar]
- Cohen, S.M.; Raymond, K.N. Catecholate/salicylate heteropodands: Demonstration of a catecholate to salicylate coordination change. Inorg. Chem 2000, 39, 3624–3631. [Google Scholar]
- Cohen, S.M.; Meyer, M.; Raymond, K.N. Enterobactin protonation and iron Release: Hexadentate tris-salicylate ligands as models for triprotonated ferric enterobactin1. J. Am. Chem. Soc 1998, 120, 6277–6286. [Google Scholar]
- Polynova, T.N.; Bel’skaya, N.P.; de Garciya Banus, D.T.; Porai-Koshits, M.A.; Martynenko, L.I. Crystal structure of the dihydrated potassium salt of aluminum ethylenediaminetetraacetate. J. Struct. Chem 1970, 11, 158–159. [Google Scholar]
- Polynova, T.N.; Zasurskaya, L.A.; Ilyukhin, A.B. Redetermination of the crystal structure of K[AlEdta].2H2O. Crystallogr. Rep 1997, 42, 168. [Google Scholar]
- Jung, W.S.; Chung, Y.K.; Shin, D.M.; Kim, S.D. Crystal and solution structure characteristics of ethylenediaminetetraacetatoaluminate(III) and gallate(III). Bull. Chem. Soc. Jpn 2002, 75, 1263–1267. [Google Scholar]
- Petrosyants, S.P.; Ilyukhin, A.B.; Malyarik, M.A. Hydrogen-bonded aggregates of scandium(III) complexes. Russ. J. Inorg. Chem 1996, 41, 1595. [Google Scholar]
- Schmitt, W.; Jordan, P.A.; Henderson, R.K.; Moore, G.R.; Anson, C.E.; Powell, A.K. Synthesis, structures and properties of hydrolytic Al(III) aggregates and Fe(III) analogues formed with iminodiacetate-based chelating ligands. Coord. Chem. Rev 2002, 228, 115–126. [Google Scholar]
- Kilyen, M.; Lakatos, A.; Latajka, R.; Labadi, I.; Salifoglou, A.; Raptopoulou, C.P.; Kozlowski, H.; Kiss, T. Al(III)-binding properties of iminodiacetic acid, nitrilotriacetic acid and their mixed carboxylic-phosphonic derivatives. J. Chem. Soc, Dalton Trans. 2002, 3578–3586. [Google Scholar]
- Ilyukhin, A.B.; Petrosyants, S.P.; Millovanov, S.V.; Malyarik, M.A. Aluminum(III) and gallium(III) complexes with methyliminodiacetic acid: Crystal structures of Cat[M(Mida)2] (Cat+ = Na, K, NH4; M3+ = Al, Ga) and M4N[Ga(Mida)2]H2O. Crystallogr. Rep 1997, 42, 958–965. [Google Scholar]
- Petrosyants, S.P.; Malyarik, M.A.; Ilyukhin, A.B. Complexation of aluminium and gallium with iminodiacetic acid in aqueous solutions: Crystal structure of diaqua di-μ-hydroxobis (iminodiacetato)di aluminium(III) and potassium bis(iminodiacetato)gallate(III). Russ. J. Inorg. Chem 1995, 40, 765. [Google Scholar]
- Jyo, A.; Kohno, T.; Terazono, Y.; Kawano, S. Crystal structure of the aluminum(III) complex of 1,4,7-Triazacyclononane-N,N′,N′-triacetate. Anal. Sci 1990, 6, 629–630. [Google Scholar]
- Bossek, U.; Hanke, D.; Wieghardt, B.K. Pendent arm macrocyclic complexes: Crystal structures of Al(TCTA) and In (TS-TACN). Polyhedron 1993, 12, 1–5. [Google Scholar]
- Soleimannejad, J.; Aghabozorg, H.; Mohammadzadeh, Y.; Hooshmand, S. 2-(2-Pyridyl) pyridinium bis(pyridine-2,6-dicarboxylato-κ3O,N,O′)aluminate(III) trihydrate. Acta Cryst 2008, E64, m870–m871. [Google Scholar]
- Valle, G.C.; Bombi, G.G.; Corain, B.; Favarato, M.; Zatta, P. Crystal and molecular structures of diaqua(nitrilotriacetato)aluminium(III) and di-μ-hydroxo-bis(nitrilotriacetato)dialuminate(III) dianion. J. Chem. Soc. Dalton Trans. 1989, 1513–1517. [Google Scholar]
- Heath, S.L.; Jordan, P.A.; Johnson, I.D.; Moore, G.R.; Powell, A.K.; Helliwell, M. Comparative X-ray and 27Al NMR spectroscopic studies of the speciation of aluminum in aqueous systems: Al(III) complexes of N(CH2CO2H)2(CH2CH2OH). J. Inorg. Biochem 1995, 59, 785–794. [Google Scholar]
- Joszai, R.; Kerekes, I.; Satoshi, I.; Sawada, K.; Zekany, L. Equilibrium and structure of the Al(III)-ethylenediamine-N,N′-bis(3-hydroxy-2-propionate) (EDBHP) complex. A multi-method study by potentiometry, NMR, ESI MS and X-ray diffraction. Dalton Trans. 2006, 3221–3227. [Google Scholar]
- Rajeswaran, M.; Blanton, T.N.; Klubek, K.P. Refinement of the crystal structure of the δ-modification of tris(8-hydroxy-quinoline)aluminum(III), δ-Al(C9H6NO)3, the blue luminescent Alq3. Z. Kristallogr 2003, 218, 439–440. [Google Scholar]
- Muccini, M.; Loi, M.A.; Kenevey, K.; Zamboni, R.; Masciocchi, N.; Sironi, A. Blue luminescence of facial tris(quinolin-8-olato)aluminum (III) in solution, crystals, and thin films. Adv. Mater 2004, 16, 861–864. [Google Scholar]
- Rajeswaran, M.; Blanton, T.N. Structure determination of a new polymorph (ɛ-Alq3) of the electroluminescence OLED (organic light-emitting diode) material, tris(8-hydroxyquinoline) aluminum(Alq3). J. Chem. Cryst 2005, 35, 71–76. [Google Scholar]
- Kim, T.S.; Kim, D.H.; Im, H.J.; Shimada, K.; Kawajiri, R.; Okubo, T.; Murata, H.; Mitani, T. Improved lifetime of an OLED using Aluminum(III) tris(8-hydroxyquinolate). Sci. Tech. Adv. Mater 2004, 5, 331–337. [Google Scholar]
- Fujii, I.; Hirayama, N.; Ohtani, J.; Kodama, K. Crystal structure of tris(8-quinolinolato) aluminum(III)-ethyl acetate (1/0.5). Anal. Sci 1996, 12, 153–154. [Google Scholar]
- Yuchi, A.; Hiramatsu, H.; Ohara, M.; Ohata, N. Performance of tris(2-methyl-8-quinolinolato) aluminum as fluorescent anionophore. Anal. Sci 2003, 19, 1177–1181. [Google Scholar]
- Iijima, T.; Yamamoto, T. Synthesis of reactive [Al(Et)(q′)2](q′ = 2-methyl-8-quinolinolato) serving as a precursor of light emitting aluminum complexes: Reactivity, optical properties, and fluxional behavior of the aluminum complexes. J. Organometal. Chem 2006, 691, 5016–5023. [Google Scholar]
- Amini, M.M.; Sharbatdaran, M.; Mirzaeeand, M.; Mirzaei, P. Synthesis, structure and luminescence study of a binuclear aluminium complex: A novel structure containing six coordinated aluminium atoms in two distinct coordination geometries. Polyhedron 2006, 25, 3231–3237. [Google Scholar]
- Albrecht, M.; Blau, O.; Fröhlich, R. Supramolecular chemistry and self-assembly special feature: “Size-selectivity” in the template-directed assembly of dinuclear triple-stranded helicates. Proc. Natl. Acad. Sci. USA 2002, 99, 4867. [Google Scholar]
- Dawson, A.; Wang, J.F.; Carducci, M.D.; Mash, E.A. Tris[2-(2-oxidophenyl)-5-phenyl-1,3,4- oxadiazole-κ2O2,N3]aluminium 0.167-hydrate. Acta Cryst 2004, E60, m1644–m1646. [Google Scholar]
- Steinhauser, S.; Heinz, U.; Bartholomä, M.; Weyhermüller, T.; Nick, H.; Hegetschweiler, K. Complex formation of ICL670 and related ligands with FeIII and FeII. Eur. J. Inorg. Chem. 2004, 4177–4192. [Google Scholar]
- Jegier, J.A.; Munoz-Hernandez, M.; Atwood, D.A. Six-coordinate aluminium cations: Synthesis, characterization and catalysis. J. Chem. Soc. Dalton Trans. 1999, 2583–2588. [Google Scholar]
- Ikeda, C.; Ueda, S.; Nabeshima, T. Aluminium complexes of N2O2-type dipyrrins: the first hetero-multinuclear complexes of metallo-dipyrrins with high fluorescence quantum yields. Chem. Commun. 2009, 2544–2546. [Google Scholar]
- Cissell, J.A.; Vaid, T.P.; Rheingold, A.L. Aluminum tetraphenylporphyrin and aluminum phthalocyanine neutral radicals. Inorg. Chem 2006, 45, 2367–2369. [Google Scholar]
- Camacho-Camacho, C.; Merino, G.; Martínez-Martínez, F.J.; Nöth, H.; Contreras, R. Syntheses and characterization by NMR spectroscopy and X-ray diffraction of complexes derived from metals of groups 2 and 13 and the ligand bis (3,5-di-tert-butyl-1-hydroxy-2-phenyl) amine. Eur. J. Inorg. Chem. 1999, 1021–1027. [Google Scholar]
- Qiao, J.; Wang, L.D.; Xie, J.F.; Lei, G.T.; Wu, G.S.; Qiu, Y. Strongly luminescent binuclear aluminium chelate with polymer-like molecular packing and solution processibility. Chem. Commun. 2005, 4560–4562. [Google Scholar]
- Tong, Y.P.; Zheng, S.L.; Chen, X.M. Syntheses, structures, and luminescent properties of isomorphous hydroxo-bridged aluminum(III) and indium(III) compounds with 2-(2-hydroxyphenyl) benzimidazole. Aust. J. Chem 2006, 59, 653–656. [Google Scholar]
- Hoveyda, H.R.; Rettig, S.J.; Orvig, C. Coordination chemistry of 2-(2′-hydroxyphenyl)-2- benzoxazole with gallium(III) and aluminum(III): Two uncommon Group 13 metal environments stabilized by a biologically relevant binding group. Inorg. Chem 1993, 32, 4909–4913. [Google Scholar]
- Langemann, K.; Heineke, D.; Rupprecht, S.; Raymond, K.N. Nordesferriferrithiocin. Comparative coordination chemistry of a prospective therapeutic iron chelating agent. Inorg. Chem 1996, 35, 5663–5673. [Google Scholar]
- Van Der Helm, D.; Baker, J.R.; Loghry, R.A.; Ekstrand, J.D. Structures of alumichrome A and ferrichrome A at low temperature. Acta Cryst 1981, B37, 323–330. [Google Scholar]
- Liu, S.; Rettig, S.J.; Orvig, C. Polydentate ligand chemistry of Group 13 metals: Effects of the size and donor selectivity of metal ions on the structures and properties of aluminum, gallium, and indium complexes with potentially heptadentate (N4O3) amine phenol ligands. Inorg. Chem 1992, 31, 5400–5407. [Google Scholar]
- Bekaert, A.; Lemoine, P.; Brion, J.D.; Viossat, B. Tris[(R)-lactamide-κ2O,O′]zinc(II) tetrabromozincate. Z. Kristallogr 2006, 221, 45. [Google Scholar]
- Babian-Kibala, E.; Chen, H.; Cotton, F.A.; Daniels, L.M.; Falvello, L.R.; Schmid, G.; Yao, Z. Synthesis and problematic crystal structures of [Al(CH3CN)6][MCl6]3(CH3CN)3 (M = Ta, Nb or Sb). Inorg. Chim. Acta 1996, 250, 359–364. [Google Scholar]
- Pfeiffer, M.; Murso, A.; Mahalakshmi, L.; Moigno, D.; Kiefer, W.; Stalke, D. Experimental and computational study on a variety of structural motifs and coordination modes in aluminium complexes of di(2-pyridyl)amides and -phosphanides. Eur. J. Inorg. Chem 2002, 2002, 3222–3234. [Google Scholar]
- Leman, J.T.; Braddock-Wilking, J.; Coolong, A.J.; Barron, A.R. 1,3-Diaryltriazenido compounds of aluminum. Inorg. Chem 1993, 32, 4324–4336. [Google Scholar]
- Braddock-Wilking, J.; Leman, J.T.; Farrar, C.T.; Cosgrove-Larsen, S.A.; Singel, D.J.; Barron, A.R. Radical anion complexes of tris(1,3-diphenyltriazenido)aluminum. J. Am. Chem. Soc 1995, 117, 1736–1745. [Google Scholar]
- Chen, P.; Li, J.; Xu, J.; Duang, F.; Deng, F.; Xu, R. Synthesis, structure and NMR characterization of a new monomeric aluminophosphate [dl-Co(en)3]2 [Al(HPO4)2(H1.5PO4)2(H2PO4)2](H3PO4)4 containing four different types of monophosphates. Solid Sate Sci. 2009, 11, 622–627. [Google Scholar]
- Azais, T.; Bonhomme, C.; Bonhomme-Coury, L.; Vaissermann, J.; Millot, Y.; Man, P.P.; Bertani, P.; Hirschinger, J.; Livage, J. Cubane shaped clusters, precursors for aluminophosphate frameworks: A solid state multinuclear NMR study, in time and frequency domains. J. Chem. Soc. Dalton Trans. 2002, 609–618. [Google Scholar]
- Azaïs, T.; Bonhomme-Coury, L.; Vaissermann, J.; Bertani, P.; Hirschinger, J.; Maquet, J.; Bonhomme, C. Synthesis and characterization of a novel cyclic aluminophosphinate: Structure and solid-state NMR study. Inorg. Chem 2002, 41, 981–988. [Google Scholar]
- Azaïs, T.; Bonhomme-Coury, L.; Vaissermann, J.; Maquet, J.; Bonhomme, C. The first aluminophosphonate cluster analogue of the 4=1 SBU of zeolites: Structure and multinuclear solid-state NMR study, including 1H NMR. Eur. J. Inorg. Chem. 2002, 2838–2843. [Google Scholar]
- Azais, T.; Bonhomme, C.; Bonhomme-Coury, L.; Kickelbick, G. Aluminophosphonate clusters: A new architecture. Dalton Trans. 2003, 3158–3159. [Google Scholar]
- Grottel, M.; Kozak, A.; Maluszyriska, H.; Pajak, Z. An X-ray and nuclear magnetic resonance study of structure and ion motions in (C(NH2)3)3AlF6. J. Phys 1992, 4, 1837. [Google Scholar]
- Adil, K.; Goreshnik, E.; Courant, S.; Dujardin, G.; Leblanc, M.; Maisonneuve, V. Synthesis and structures of new hybrid fluorides templated by tetraprotonated pentaerythrityl tetramine. Solid State Sci. 2004, 1229–1235. [Google Scholar]
- Adil, K.; Leblanc, M.; Maisonneuve, V. Structural chemistry of organically-templated metal fluorides. J. Fluorine Chem 2006, 127, 1349–1354. [Google Scholar]
- Bourosh, P.N.; Koropchanu, E.B.; Simonov, Y.; Gdaniec, M.; Bologa, O.A.; Gerbeleu, N.V. Cobalt(III) α-dimethylglyoximates [Co(DH)2(Py)2]2SiF6·10H2O and [Co(DH)2(Thio)2]2SiF6· 2H2O·C2H5OH: Synthesis and structure. Russ. J. Inorg. Chem 2002, 7, 1604. [Google Scholar]
- Touret, J.; Bourdon, X.; Leblanc, M.; Retoux, R.; Renaudin, J.; Maisonneuve, V. Crystal structure of new hydroxide fluorides with isolated F-anions: [H3N(CH2)6NH3]2M(F,OH)6(F,OH)· H2O (M = Al, In). J. Fluorine Chem 2001, 110, 133–138. [Google Scholar]
- Adil, K.; Marrot, J.; Leblanc, M.; Maisonneuve, V. Diethylenetriaminium hexafluoroaluminate dehydrate. Acta Cryst 2005, E61, m1178–m1180. [Google Scholar]
- Fourquet, J.L.; Plet, F.; Paper, R.D. The structure of dimercury(I) alluminium(III) fluoride dehydrate. Rev. Chim. Miner 1986, 23, 183. [Google Scholar]
- Goreshnik, E.; Leblanc, M.; Maisonneuve, V. 1,4,8,11-Tetraazacyclodecane-1,4,8,11-tetraium bis(aquapentafluoroaluminate) dehydrate. Acta Cryst 2003, E59, m1059–m1061. [Google Scholar]
- Cadiau, A.; Hemon-Ribaud, A.; Leblanc, M.; Maisonneuve, V. 2,4,6-Triamino-1,3,5-triazine- 1,3-diium aquapentafluoridoaluminate. Acta Cryst 2008, E64, m523–m524. [Google Scholar]
- Adil, K.; Leblanc, M.; Maisonneuve, V. Tris(2-ammonioethyl)aminium decafluorominium monohydrate, (H4tren)[Al2F10]·H2O. Acta Cryst 2004, E60, m1379–m1381. [Google Scholar]
- Tang, L.Q.; Dadachov, M.S.; Zou, X.D. SU-12: A silicon-substituted ASU-16 with circular 24-rings and templated by a monoamine. Z. Kristallogr 2001, 216, 385–386. [Google Scholar]
- Goreshnik, E.; Leblanc, M.; Maisonneuve, V. From isolated polyanions to 1-D structure: Synthesis and crystal structure of hybrid fluorides {[(C2H4NH3)3NH]4+}2·(H3O)+·[Al7F30]9− and {[(C2H4NH3)3NH]4 +}2·[Al7F29]8− ′ (H2O)2. Z. Anorg. Allg. Chem 2002, 628, 162–166. [Google Scholar]
- Dimitrov, A.; Heidemann, D.; Kemnitz, E. F/Cl-Exchange on AlCl3-pyridine adducts: Synthesis and characterization of trans-difluoro-tetrakis-pyridine-aluminum-chloride, [AlF2(Py)4]+Cl−. Inorg. Chem 2006, 45, 10807–10814. [Google Scholar]
- Krossing, I.; Raabe, I. Noncoordinating anions—Fact or fiction? A survey of likely candidates. Angew. Chem. Int. Ed 2004, 43, 2066–2090. [Google Scholar]
- Gonsior, M.; Krossing, I.; Müller, L.; Raabe, I.; Jansen, M.; van Wüllen, L. PX4 +, P2X5 +, and P5X2 + (X = Br, I) salts of the superweak Al(OR)4 − anion [R = C(CF3)3]. Chem. Eur. J 2002, 8, 4475–4492. [Google Scholar]
- Krossing, I. The facile preparation of weakly coordinating anions: Structure and characterisation of silverpolyfluoroalkoxyaluminates AgAl(ORF)4, calculation of the alkoxide ion affinity. Chem. Eur. J 2001, 7, 490–502. [Google Scholar]
- Santiso-Quiñones, G.; Brückner, R.; Knapp, C.; Dionn, I.; Passmore, J.; Krossing, I. Cyclododecasulfur as a ligand: From gas-phase experiments to the crystal structures of [Cu(S12)(S8)]+ and [Cu(S12)(CH2Cl2)]+. Angew. Chem. Int. Ed 2009, 48, 1133–1137. [Google Scholar]
- Santiso-Quiñones, G.; Higelin, A.; Schaefer, J.; Brückner, R.; Knapp, C.; Krossing, I. Cu[Al(ORF)4] starting materials and their application in the preparation of [Cu(Sn)]+ (n = 12, 8) complexes. Chem. Eur. J 2009, 15, 6663–6677. [Google Scholar]
- Lewinski, J.; Zachara, J.; Kopec, T.; Madura, I.; Prowotorow, I. On the mechanism of four-coordinate aluminum alkyls interaction with dioxygen: Evidence for spatial demands in the autoxidation reaction. Inorg. Chem. Commun 1999, 2, 131–134. [Google Scholar]
- Kendall, R.A.; Dunning, T.H., Jr; Harrison, R.J. Electron affinities of the first-row atoms revisited. Systematic basis sets and wave functions. J. Chem. Phys. 1992, 96, 6796–6806. [Google Scholar]
- Woon, D.E.; Dunning, T.H., Jr. Gaussian basis sets for use in correlated molecular calculations. III. The second row atoms, Al-Ar. J. Chem. Phys. 1993, 98, 1358–1371. [Google Scholar]
- Haraguchi, H.; Fujiwara, S. Aluminum complexes in solution as studied by aluminum-27 nuclear magnetic resonance. J. Phys. Chem 1969, 78, 3467–3473. [Google Scholar]
- Kon’shin, V.V.; Chernyshov, B.N.; Ippolitov, E.G. Composition and structure of aluminum fluorocomplexes in aqueous solutions of hydrogen peroxide and inorganic acids. Russ. Chem. Bull 1987, 36, 1577–1581. [Google Scholar]
- Müller, D.; Bentrup, U. 27Al-NMR-Untersuchungen an Alkalifluoroaluminaten. Z. Anorg. Allg. Chem 1989, 575, 17–25. [Google Scholar]
- Chen, J.L.; Noodleman, L.; Case, D.A.; Bashford, D. Incorporating solvation effects into density functional electronic structure calculations. J. Phys. Chem. 1994, 98, 11059–11068. [Google Scholar]
- Tomasi, J.; Mennucci, B.; Cammi, R. Quantum mechanical continuum solvation models. Chem. Rev 2005, 105, 2999–3093. [Google Scholar]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Montgomery, J.A., Jr.; Vreven, T.; Kudin, K.N.; Burant, J.C.; et al. Gaussian 03 Revision B.05; Gaussian Inc: Wallingford, CT, USA, 2004. [Google Scholar]
- Vosko, S.H.; Wilk, L.; Nusair, M. Accurate spin-dependent electron liquid correlation energies for local spin density calculations: a critical analysis. Can. J. Phys 1980, 58, 1200–1211. [Google Scholar]
- Stephens, P.J.; Devlin, F.J.; Chabalowski, C.F.; Frisch, M.J. Ab initio calculation of vibrational absorption and circular dichroism spectra using density functional force fields. J. Phys. Chem 1994, 98, 11623–11627. [Google Scholar]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev 1988, B37, 785–789. [Google Scholar]
- Becke, A.D. Density functional thermochemistry. III. The role of exact exchange. J. Chem. Phys 1993, 98, 5648–5652. [Google Scholar]
- Møller, C.; Plesset, M.S. Note on an approximation treatment for many-electron systems. Phys. Rev 1934, 46, 618–622. [Google Scholar]
- Francl, M.M.; Pietro, W.J.; Hehre, W.J.; Binkley, J.S.; Gordon, M.S.; DeFrees, D.J.; Pople, J.A. Self-consistent molecular orbital methods. 23. A polarization basis set for second row elements. J. Chem. Phys 1982, 77, 3654–3665. [Google Scholar]
- McLean, A.D.; Chandler, G.S. Contracted Gaussian basis sets for molecular calculations. I. Second row atoms, Z = 11–18. J. Chem. Phys 1980, 72, 5639–5648. [Google Scholar]
- Robinson, M.; Haynes, P.D. Dynamical effects in ab initio NMR calculations: Classical force fields fitted to quantum forces. J. Chem. Phys 2010, 133, 084109. [Google Scholar]





| Species a | Refs. | 27Al chemical shifts | ||||
|---|---|---|---|---|---|---|
| GIAOB3LYP/ 6-31G(d) b | GIAOB3LYP/ 6-311+G(d,p) b | GIAOHF/6-311+ G(d,p) b | GIAO-B3LYP/6-31G(d)//B3LYP/6-31G(d) c | Expt.d | ||
| Chemical shift reference | ||||||
| [Al(OH2)6]3+ | [20–24] | 0 ± 2.87 | 0 ± 3.44 | 0 ± 2.99 | 0 | 0 |
| Al(III) hydrolysis products | ||||||
| [Al2(μ2-OH)2(OH2)8]4+ | [25] | 0.74 ± 1.94 | 1.73 ± 0.11 | −1.30 ± 2.35 | 3.23 | 4.2 |
| [Al8(μ3-OH)2(μ2-OH)12(OH2)16]10+ | [26] | 0.34 ± 0.39 | 4.8 (MAS) | |||
| 5.67 ± 0.11 | 8.4 | |||||
| 9.53 ± 0.10 | 11 | |||||
| [AlO4Al12(μ2-OH)24(OH2)12]7+ (Keggin-Al13) | [25] | 52.95 ± 0.02 | 61.50 ± 0.52 | 57.30 | 63.5 | |
| 7.05 ± 0.53 | 6.53 ± 0.67 | 4.52 ± 0.65 | 12 | |||
| [Al13(μ3-OH)6(μ2-OH)12(OH2)6]15+ (flat-Al13) | [27] | 15.74 | ||||
| 9.71 ± 0.79 | ||||||
| 0.25 ± 0.32 | ||||||
| [Al30(μ4-O)8(μ3-OH)6(μ2-OH)50(OH2)24]15+ (Al30) | [25] | 4.08 ± 1.18 | 4 | |||
| 8.57 ± 0.41 | 5~12 | |||||
| 64.38 ± 0.51 | 64.5 | |||||
| Al(III) complexation with carboxylate and carbonyl groups | ||||||
| [AlL6]3−, L = formate | [28] | 0.92 | −4.12 | −2.56 | ||
| [AlL6]3+, L = dimethylformamide | [29,30] | 3.20 ± 0.46 | −0.78 ± 0.60 | 0.42 ± 0.41 | ||
| [AlL6]3+, L = dimethylacetamide | [31] | −6.97 | −16.13 | −15.50 | ||
| [AlL3]3−, L = oxalate | [32–39] | 13.35 ± 0.97 | 14.77 ± 0.97 | 15.43 ± 1.12 | 20.15 | 16.3 |
| [AlL2(OH2)2]−, L = malonate | [40] | 4.81 | 4.32 | 3.65 | 19.77 | 2.5 |
| [AlL2(OH2)2]−, L = methylmalonate | [21] | 8.29 | 2.93 | 4.14 | ||
| [AlL3]3+, L = acetylacetone | [41–44] | 2.44 ± 0.84 | −2.29 ± 0.50 | −0.40 ± 0.87 | 0.88 | |
| [AlL3]3+, L = 1,3-diphenylpropane-1,3-dione | [45] | 7.39 | −0.37 | 2.15 | ||
| [AlL3]3+, L = 1,3-dimesitylpropane-1,3-dione | [46] | 5.26 | −0.38 | 1.65 | ||
| [AlL3]3+, L = 1,3-bis(pentafluorophenyl)propane-1, 3-dione | [47] | 2.39 | −1.52 | 0.37 | ||
| [AlL3]3+, L = methylacetoacetate | [48] | 6.54 | 2.60 | 2.60 | ||
| [AlL3]3+, L = t-butylacetoacetate | [49] | 3.74 | −0.91 | −1.17 | ||
| [AlL3]3+, L = 3-(4-pyridyl)-2,4-pentanedione | [50] | 2.17 | −3.12 | −0.40 | ||
| [AlL3]3+, L = 3-phenyl-2,4-pentanedione | [50] | 2.53 | −3 | −0.51 | ||
| AlL3, L = iso-maltol | [51] | 5.98 | 1.22 | 1.37 | 12.60 | 2.9 |
| Al(III) complexation with catechol-like ligands | ||||||
| AlL3, L = maltol | [52] | 34.10 ± 0.17 | 39.04 ± 0.13 | 31.82 ± 0.12 | 43.36 | 37, 38 |
| AlL3, L = 2-ethylmaltol | [53] | 33.86 | 38.80 | 31.48 | 43.74 | 38 |
| [AlL]3−, L = tris(N,N′-diethyl-2,3-dihydroxoterephthalamide)diamine | [54] | 30.30 | 32.66 | 26.75 | 26 | |
| AlL3, L = 3-hydroxy-2-pyridone | [55] | 24.09 | 33.43 | 27.05 | ||
| AlL3, L = 1,2-dimethyl-3-hydroxy-4-pyridone | [56,57] | 32.32 ± 0.00 | 37.04 ± 0.00 | 28.75 ± 0.00 | 36, 39 | |
| AlL3, L = 1-n-propyl-2-methyl-3-hydroxy-4-pyridone | [58] | 31.80 | 35.76 | 28.37 | 37 | |
| AlL3, L = 1-n-butyl-2-methyl-3-hydroxy-4-pyridone | [58] | 31.21 | 35.51 | 27.77 | 37 | |
| AlL3, L = 1-p-tolyl-2-methyl-3-hydroxy-4-pyridone | [59] | 33.74 | 38.55 | 30.39 | 37 | |
| AlL3, L = tropolone | [60] | 32.68 | 36.11 | 29.72 | 42.72 | 36.6 |
| AlL3, L = 6-i-propyltropolone | [61] | 33.42 | 36.50 | 29.84 | ||
| Al2L3, L = 1,3-bis((3-oxy-1-methyl-2-oxo-1,2-dihydropyridin- 4-yl)carboxamido)-2,2-dimethylpropane | [62] | 28.67 ± 0.00 | 34.18 ± 0.00 | |||
| [Al2(μ2-O)2 L4]4−, L =1,2-dihydroxyanthraquinone | [63] | 23.01 ± 0.00 | ||||
| [Al2(μ2-O)2 L4]4−, L =1,2,4-trihydroxyanthraquinone | [64] | 23.67 ± 0.05 | 23.1 | |||
| Al(III) complexation with carboxylate and hydroxyl groups | ||||||
| mer-[AlL3]3−, L = glycolate | [65] | 30.86 | 37.08 | 28.13 | ||
| fac-[AlL3]3−, L = glycolate | [66] | 27.65 | 31.59 | 23.55 | 34.00 | 25.5 |
| [AlL3]3−, L = lacate | [67] | 23.12 ± 0.13 | 26.32 ± 0.26 | 21.16 ± 0.16 | 33.44 | 24 |
| [AlL2]5−, L = H−1citrate | [68,69] | 19.07 ± 0.45 | 18.04 ± 0.68 | 17.33 ± 0.71 | 25.69 | 21.4 |
| [Al2L3]6−, L = H−1citrate | [70] | 25.36 | 20.72 | 17.98 | ||
| 20.28 | 14.44 | 11.40 | ||||
| [Al3L3(μ2-OH)(OH2)]4−, L = H−1citrate | [71] | 3.43 | −0.44 | 0.05 | 20.74 | 0.6 |
| 14.42 | 9.81 | 9.32 | 22.00 | 10.9 | ||
| 15.90 | 9.81 | 8.41 | 23.00 | 12.9 | ||
| [Al3L2(μ2-OH)2(OH2)4]−, L = H−1citrate | [20] | 5.43 ± 0.70 | ||||
| 25.75 | ||||||
| [Be2Al2L4]6−, L = H−1citrate | [72] | 17.79 ± 0.87 | 14.0 | |||
| [Be6Al6L6]18−, L = H−1citrate | [72] | 3.07 ± 0.18 | 12.2 | |||
| [Al4L6]6−, L = H−1malate | [73] | 23.27 ± 0.00 | 20.20 ± 0.00 | 15.83 ± 0.00 | 17.2 | |
| 6.35 ± 0.00 | 1.14 ± 0.00 | 1.18 ± 0.00 | 1.6 | |||
| [Al4L4(μ2-OH)2]2−, L = H−1malate | [73] | 25.10 ± 0.79 | 28.46 ± 0.87 | 21.02 ± 1.06 | 2.2,1.6 | |
| 5.59 ± 1.02 | 1.83 ± 1.28 | 1.80 ± 1.11 | 1.1 | |||
| [Al2L2(OH2)2]2−, L = H−1saccharate | [74] | 28.61 ± 0.00 | 29.21 ± 0.00 | 24.36 ± 0.00 | 65.49 | |
| [Al6L4(μ2-OH)8]6−, L = H−4galactarate | [75] | 16.43 ± 2.40 | 17.82 ± 1.13 | 11.64 ± 1.12 | 16.1, 16.8, 17.4, 17.7 (MAS) | |
| 20.54 ± 1.74 | 21.27 ± 1.14 | 15.86 ± 1.75 | 22.6, 21.9 (MAS) | |||
| Al2L2(μ2-t-butoxo)2(t-butyoxy-t-butylperoxy), L = o-methoxycarbonyl phenoxy | [76,77] | 11.91 ± 0.00 | 3.99 ± 0.00 | 3.94 ± 0.01 | ||
| 62.46 ± 0.00 | 61.47 ± 0.01 | 64.46 ± 0.01 | ||||
| [AlL2L′2]−, L = acetylacetonate, L′ = iso-propoxo | [78] | 9.25 | 2.89 | 4.44 | ||
| Al2L4L′2, L = 3,5-heptanedionato, L′ = iso-propoxo | [79] | 9.69 ± 0.00 | 4.71 ± 0.00 | 2.40 ± 0.00 | ||
| [AlL]+, L = (2-hydroxybenzoyl-2-aminoethyl)-bis (2,3-dihydroxybenzoyl-2-aminoethyl)ammonio | [80] | 8.05 | 1.26 | 3.95 | ||
| [AlL]+, L = tris((2-Hydroxybenzoyl)-2-aminoethyl)ammine | [81] | 7.04 | 0.38 | 2.64 | ||
| [AlL]+, L = tris((2-Hydroxy-3-methoxybenzoyl)-2- aminoethyl)ammine | [81] | 6.05 | 0.27 | 2.24 | ||
| Al(III) complexation with polyamino-polycarboxylates | ||||||
| [AlL]−, L = ethylenediaminetetraacetate | [82–84] | 40.87 ± 2.57 | 42.22 ± 1.67 | 36.49 ± 1.27 | 47.88 | 41.2 |
| [AlL2]−, L = iminodiacetate | [85–87] | 37.94 ± 0.66 | 41.68 ± 0.60 | 35.15 ± 0.42 | 41.69 | 36.5 |
| [AlL2]−, L = methyliminodiacetate | [88] | 41.69 ± 0.62 | 43.18 ± 0.91 | 36.82 ± 0.63 | ||
| Al2L2(μ2-OH)2(OH2)2, L = iminodiacetate | [86,89] | 20.12 ± 0.67 | 22.07 ± 1.60 | 18.56 ± 1.03 | ||
| AlL, L = 1,4,7-triazacyclononane-N,N′,N″-triacetate | [90,91] | 52.17 ± 0.82 | 49.37 ± 1.44 | 44.68 ± 0.73 | ||
| [AlL2]−, L = dipicolinate | [92] | 22.62 | 27.33 | 23.22 | ||
| AlL(OH2)2, L = nitrilotriacetate | [93] | 24.77 | 25.74 | 21.60 | ||
| [Al2L2(μ2-OH)2]2−, L = nitrilotriacetate | [93] | 27.42 ± 0.00 | 26.82 ± 0.00 | 22.16 ± 0.00 | 40.27 | 25.4 |
| Al2L2(OH)2, L = N-(2-oxyethyl)iminodiacetate | [94] | 30.05 ± 0.00 | 28.59 ± 0.00 | 24.17 ± 0.00 | 32.8 | |
| Al2L2(μ2-OH)2, L = ethylene-N,N′-bis(3-hydroxy propionato) | [95] | 29.00 ± 1.69 | 27.50 ± 1.33 | 24.23 ± 1.41 | 38.74 | 25~30 |
| [Al4L2(μ2-OH)4]2−, L = 1,3-diamino-2-propanolato-N,N,N′,N′-tetraacetato | [86] | 27.26 ± 1.69 | 25.83 ± 1.00 | 19.69 ± 0.56 | ||
| [Al4L2L′2(μ2-OH)(μ2-O)]−, L = N-(3-ammoniopropyl)carbamato, L′ = 1,3-diamino-2-propanolato- N,N,N′,N′-tetraacetato | [86] | 30.00 ± 0.50 | 27.11 ± 1.36 | 22.54 ± 0.15 | ||
| Al(III) complexation with mixed O and N ligands | ||||||
| AlL3, L = 8-hydroxyquinoline | [96–100] | 30.68 ± 1.84 | 31.27 ± 1.37 | 29.39 ± 1.68 | 40.41 | 31.1 |
| AlL3, L = 2-methyl-8-hydroxyquinoline | [101] | 33.28 | 35.11 | 31.33 | ||
| AlL2L′, L = 2-methyl-8-hydroxyquinoline, L′ = picolinato | [102] | 28.81 | 29.78 | 26.97 | ||
| Al2L4(μ2-2-(ethoxy)ethoxo))2, L = 8-hydroxyquinoline | [103] | 28.14 ± 0.44 | 24.82 ± 1.21 | 22.39 ± 1.29 | 37.52 | 26.9 |
| Al2L3, L = 1,3-bis(8-hydroxyquinolin-7-yl)-2-methylenepropane | [104] | 33.55 ± 0.00 | 34.88 ± 0.00 | 31.92 ± 0.00 | ||
| AlL3, L = 2-(2-hydroxyphenyl)-5-phenyl-1,3,4-oxadiazole | [105] | 8.95 | −0.96 | 3.41 | ||
| [AlL2]−, L = 1-phenyl-3,5-bis(2-oxyphenyl)-1,2,4-triazole | [106] | 6.91 | 0.85 | 2.80 | ||
| [AlL2(OH2)2]+, L = N,N′-bis(3,5-di-tbutylsalicylidene) ethylenediamine | [107] | 7.41 | 5.02 | 8.07 | ||
| [AlL2(CH3OH)2]+, L = N,N′-bis(3,5-di-tbutylsalicylidene) ethylenediamine | [107] | 11.62 ± 1.47 | 8.59 ± 2.08 | 9.40 ± 1.21 | ||
| [AlL2(OH2)2]−, L = 1,9-bis(2-oxyphenyl)-5-phenyldipyrrine | [108] | 6.67 | 3.16 | 5.88 | ||
| AlLL′2, L = 5,10,15,20-tetraphenylporphyrine, L′ = tetrahydrofuran | [109] | −5.41 | −15.23 | −10.73 | ||
| AlL2, L = 3,5-di-t-butyl-1,2-quinone-1-(2-hydroxy-3,5-di-tbutylphenyl) imine | [110] | 50.61 | 50.41 | 41.14 | ||
| AlL2L′2, L =2,2,6,6-tetramethylheptane-3,5-dionato, L′ = 2-((2-hydroxy)benzylidene)amino)phenolato | [111] | 12.17 ± 0.00 | 7.15 ± 0.00 | 6.82 ± 0.00 | ||
| Al2L4(μ2-OH)2, L = 2-(2-oxyphenyl)benzimidazole | [112] | 7.96 ± 0.00 | 1.56 ± 0.00 | 2.80 ± 0.00 | ||
| Al2L4(μ2-OH)2, L = 2-(2′-hydroxyphenyl)-2-benzoxazolato | [113] | 14.92 ± 0.21 | ± 0.00 | 8.12 ± 0.05 | 5 | |
| [AlL2]−, L = nordesferriferrithiocin | [114] | 19.95 | 17.46 | 16.86 | ||
| [AlL2]−, L = desferriferrithiocin | [114] | 12.84 | 4.89 | 7.58 | ||
| AlL, L = alumichrome A | [115] | 26.96 | 31.54 | |||
| [AlL]+, L =tris(5′-chloro-2′-hydroxybenzylaminoethyl)amine | [116] | 19.87 | 11.25 | 13.95 | ||
| [Al3(μ3-O)L6L′3]+, L = acetate, L′ = acetonitrile | [116] | 2.66 ± 0.24 | −1.08 ± 0.17 | −0.16 ± 0.57 | ||
| Al(III) complexation with N's | ||||||
| [AlL6]3+, L = acetonitrile | [118] | −20.44 ± 2.21 | −37.13 ± 1.12 | −27.74 ± 1.59 | −14.60 | −33 |
| AlL3, L = bis(2-pyridyl)amido | [119] | 28.36 | 20.50 | 23.19 | ||
| AlL3, L = 1,3-bis(2-methylphenyl)triazenido | [120] | 28.62 | 16.35 | 21.86 | 41.93 | 28 |
| AlL3, L = 1,3-bis(4-chlorophenyl)triazenido | [120] | 28.62 | 23.05 | 23.15 | 26 | |
| AlL3, L = 1,3-bis(4-methoxyphenyl)triazenido | [120] | 26.60 | 20.75 | 21.82 | 41.48 | 27 |
| AlL3, L = 1,3-diphenyltriazenido | [121] | 26.72 | 21.26 | 21.82 | 25 | |
| Al(III) complexation with P and other ligands | ||||||
| [Al(H2L)3(HL)3]6−, L = phosphate | [122] | −9.22 | 10.78 | −14.88 | −15.2 | |
| [Al4(HL)4L′12]4+, L = phosphate, L′ = ethanol | [123] | 1.32 ± 0.00 | −8.7, −8.8 (MAS) | |||
| 1.77 ± 0.00 | −8.2 | |||||
| [Al2L2L′8]4+, L = phenylphosphinato, L′ = n-butanol | [124] | 4.91 ± 0.00 | 2.04 ± 0.00 | 0.09 ± 0.00 | −2.5 | |
| [Al3L2L′10(μ2-OH)]4+, L = phenylphosphinato, L′ = ethanol | [125] | −0.02 | −2.2 | |||
| 3.42 ± 0.69 | 1.5 | |||||
| [Al5L4L′10(μ2-OH)2]5+, L = phenylphosphinato, L′ = sec-butanol | [126] | −0.32 ± 0.07 | 0 | |||
| 40.99 | 48.7 | |||||
| Al(III)-fluoride complexes | ||||||
| [AlF6]3− | [127–132] | 17.60 ± 0.84 | −1.05 ± 0.88 | −4.77 ± 1.22 | −5, −0.1, −0.6, −2.4, −2.7, −2.8, −17.9, | |
| [AlF5(OH2)]2− | [129, 133–135] | 17.46 ± 1.26 | 5.18 ± 1.46 | −0.05 ± 2.33 | −6.3, −12.0, −13.8, −14.4 | |
| [Al2F10]4− | [136,137] | 18.35 ± 0.97 | ||||
| [Al4F18]6− | [129] | 12.62 ± 0.06 | ||||
| [Al7F30]9− | [138] | −3.59 | ||||
| 12.16 ± 0.29 | ||||||
| [AlF2L4]+, L = pyridine | [139] | 6.74 ± 0.47 | 2.10 ± 1.75 | 4.19 ± 0.04 | 13.53 | 3.6 (MAS) |
| Tetrahedral-coordinated Al(III) with O's | ||||||
| [Al(OR)4]−, R = C(CF3)3 | [140–143] | 40.55 | 33.09 | 38.36 | 51.71 | 38.8 |
| 41.41 | 33.35 | 38.80 | 36.2 | |||
| 39.71 | 32.22 | 36.79 | 37.5 | |||
| 36.58 | ||||||
| 35.84 | 26.16 | 32.88 | 36 | |||
| 41.08 | 29.83 | 38.56 | 33.8 | |||
| 31.80 | 21.82 | 27.67 | 34.1 | |||
| 39.66 | 31.83 | 36.86 | 34.1 | |||
| 41.91 | 39.54 | |||||
| [Al(OR)4]−, R = CH(CF3)2 | [142,144] | 58.23 ± 0.33 | 56.30 ± 0.11 | 58.42 ± 0.64 | 69.97 | 58 |
| 61.18 | 60.69 | 61.91 | 58 | |||
| 55.61 | 52.74 | 54.95 | 56.9 | |||
| [Al(OR)4]−, R = C(CH3)(CF3)2 | [142,144] | 50.29 | 45.58 | 49.88 | 45.2 | |
| 50.71 | 44.95 | 49.34 | 45.6 | |||
| [(OR)3Al FAl(OR)3]−, R = C(CF3)3 | [141] | 32.62 ± 1.47 | 27.89 ± 1.89 | 33.22 ± 2.21 | 46.30 | 36 |
| Tetrahedral-coordinated Al(III) with C's and N's | ||||||
| Al2L2L′4, L = pyrazolyl, L′ = t-butyl | [145] | 143.64 ± 0.00 | 146.56 ± 0.00 | 148.74 ± 0.00 | 143.42 | 150 |
| Al2L2L′4, L = 3,5-dimethylpyrazolyl, L′ = methyl | [77] | 140.62 ± 0.00 | 164.46 ± 0.00 | 158.22 ± 0.00 | 139.69 | 150 |
| AlLL′2, L = 1,3-diphenyltriazenido, L′ = iso-butyl | [120] | 170.36 | 189.01 | 178.95 | ||
| AlLL′2, L = 1,3-diphenyltriazenido, L′ = 2,6-di-t-butyl-4-methylphenoxy | [120] | 41.52 | 44.09 | 50.88 | 45.65 | 31 |
| Penta-coordinated Al(III) complexes | ||||||
| [AlL]2−, L = (2-hydroxy-3-methoxybenzoyl-2-aminoethyl)-bis(2,3-dihydroxybenzoyl-2-aminoethyl)amine | [79] | 51.30 | 53.08 | |||
| [AlL]2−, L = (2-hydroxybenzoyl-2-aminoethyl)-bis(2,3-dihydroxybenzoyl-2-aminoethyl)amine | [79] | 56.30 | ||||
| AlLL′, L = N,N′-ethylene-bis(salicylideneamino-), L′ = methyl | [119] | 61.12 | 66.86 | 64.69 | ||
| B2Al2(μ2-ethoxo)L4L′6, L = pyrazolyl, L′ = ethyl | [77] | 67.85 ± 0.00 | 68.09 ± 0.00 | 66.20 ± 0.00 | 72.01 | 62 |
© 2012 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Wang, X.; Wang, C.; Zhao, H. Errors in the Calculation of 27Al Nuclear Magnetic Resonance Chemical Shifts. Int. J. Mol. Sci. 2012, 13, 15420-15446. https://doi.org/10.3390/ijms131115420
Wang X, Wang C, Zhao H. Errors in the Calculation of 27Al Nuclear Magnetic Resonance Chemical Shifts. International Journal of Molecular Sciences. 2012; 13(11):15420-15446. https://doi.org/10.3390/ijms131115420
Chicago/Turabian StyleWang, Xianlong, Chengfei Wang, and Hui Zhao. 2012. "Errors in the Calculation of 27Al Nuclear Magnetic Resonance Chemical Shifts" International Journal of Molecular Sciences 13, no. 11: 15420-15446. https://doi.org/10.3390/ijms131115420
APA StyleWang, X., Wang, C., & Zhao, H. (2012). Errors in the Calculation of 27Al Nuclear Magnetic Resonance Chemical Shifts. International Journal of Molecular Sciences, 13(11), 15420-15446. https://doi.org/10.3390/ijms131115420