3.1. Water Molecule
We will begin by considering a water molecule to exemplify how to interpret LRF-BO values.
The computational values of the LRF-BO for the water molecule are summarized in
Figure 1. When the virtual perturbation is applied to the oxygen site, the LRF-BO value for both of the OH bonds is 1.456 as shown in
Figure 1a. When the perturbation is applied to the left hydrogen site (H
1), the LRF-BO values of two O-H bonds are different each other, i.e.,
and
(
Figure 1b). Naturally, the left and right become reverse for the perturbation to the right hydrogen (H
2), i.e.,
and
, which are shown in
Figure 1c.
A positive value of
indicates that if the virtual perturbation (
) is repulsive for electrons, the bond order increases, and that if the virtual perturbation is attractive for electrons, the bond-order decreases. This is because the following relation holds:
Then, for the case of
Figure 1a, the LRF-BO value,
, indicates not only that the repulsive potential to the oxygen site strengthens O-H bonds of water, but also that the attractive potential weakens the bond, of which situations are illustrated in
Figure 2a. Similarly, the meaning of
values shown in
Figure 1b is two-fold, as shown in
Figure 2b.
We summarized the relation among the sign of the LRF-BO values, the sign of the perturbation, and the change of the bond-order in
Table 1. For a specific LRF-BO value, there are two cases concerning the sign of the virtual perturbation, which leads to two situations for the molecular system. Thus, we have to choose the sign of the virtual perturbation that is appropriate for the situation we consider. For example, it can be deduced from
Figure 2(a2),(b1) that an attractive
and an repulsive
induce the dissociation of the O-H
1 bond of the water molecule, which corresponds to a decrease of the p
Ka value of water due to the ligation of H
2O to a metal ion, which is a well-known fact in inorganic chemistry [
26],
For the reaction in water solution, this chemical reaction formula is rewritten in a more realistic form,
For instance, when a water molecule ligates to
, the p
Ka value decreases from 14.0 to 10.0 [
26]. As an interpretation of the LRF-BO results shown in
Figure 2(a2),(b1), the attractive
plays the role of the Zn
2+ ion and the repulsive
the role of the oxygen site of the additional H
2O at the left side of Equation (16) to receive the proton and to form the hydronium ion. What we would like to emphasize here is that the signs of the virtual perturbation should be appropriately determined when we interpret calculated LRF-BO values in the context of chemical reactions.
In the remaining part, the virtual perturbation will be assumed to be repulsive for electrons unless stated otherwise.
3.2. Various Types of Chemical Bonds
We first calculated the LRF-BO values of H
2 and H-X (X = F, Cl, Br, I) to check dependency of LRF-BO values on polarity of covalent bonds. For H
2, the calculated LRF-BO value becomes zero. This fact is straightforwardly derived from Equation (1): the leading term of the linear response function of density matrix is given by,
Here,
and
are atomic orbitals of hydrogens of H
2. As can be seen from Equation (17), the cross terms,
and
, disappear, which makes
, and so
, zero. In contrast, the LRF-BO values of the halogen halides are non-zero: when the case that the perturbation is applied to the hydrogen atom the values,
, of H-X (X= F, Cl, Br, I) are −2.132, −1.358, −0.58724, and −0.300, respectively. In
Figure 3, we show the relation between the calculated Mulliken charges on the hydrogen atom and the
values. From this figure, we can see that a linear relationship holds. Note that this relation holds only for simple two-center two-electrons polar covalent systems (for details of the analysis of the results, see
Appendix A). We would like to point out that the negative
values indicate that repulsive potentials to electrons on hydrogen atoms induced the dissociation of the bonds, being consistent with a reasonable picture of chemical reactions.
Next, we investigated coordination bonding systems. It is known that a ligand that lies trans to the leaving group increases the rate of the substitution if the ligand is a strong donor or a strong π acceptor. This is called the trans-effect, which is described in most standard text books of inorganic chemistry [
27,
28]. A typical example is the reaction step to yield cisplatin, which is illustrated in
Figure 4a. In this case, it is known that the substitution reaction occurs next to the ammonium ligand (NH
3), not trans to NH
3, because the trans effect of Cl
− is larger than that of NH
3 [
27]. In order to check whether the LRF-BO values could be an indicator to the trans-effect, we calculated the LRF-BO values,
for [Pt(NH
3)Cl
3]
−, the geometry of which is optimized with the B3LYP method. We employed the LANL2TZ(f) basis set for Pt atom, and 6-311G** basis sets for other atoms. As shown in
Figure 4b, the obtained
values are 6.064, 5.890, 5.952, and 2.091, for X = Cl(1), Cl(2), Cl(3), and NH
3, respectively. On the basis of these results, the substitution reaction is predicted to occur at the Cl(1) site, not the Cl(2) site, being consistent with the substitution reaction to yield cisplatin. We have to comment that that non-negligible difference between
and
is due to the position of protons of NH
3: one of the protons lies within the planar consisting of Pt, N, and three Cl atoms, nearby Cl(1), enhancing
. We further examined the LRF-BO values of [PtXCl
3]
2− for, X = Cl, Br, I, the results of which are presented in
Figure 4c–e. The point is that the calculated LRF-BO values are in order,
, being consistent with the trans-effect series of halogen ions,
[
28]. In addition, it is noteworthy that all the values
are positive, implying that an electrophilic attack induces the elimination of the leaving ions or the leaving group (see
Table 1): in short, the LRF-BO values provide a reasonable qualitative picture of the chemical reactions as well.
3.3. Inductive and Resonance Effects of Organic Molecules
Next, we calculated the LRF-BOs of the saturated and unsaturated (conjugated) molecules, which has been one of the standard systems for testing of the applicability of the linear response function of density (LRF-D) to inductive and resonance effects of organic molecules [
9,
14]. For this purpose, we picked out hexan-1-ol and hexa-1,3,5-trien-1-ol, the molecular structures of which are illustrated in
Figure 5a,b. Before testing the LRF-BO values, we computed atom-condensed LRF-D values, which are defined by,
Here K-th and L-th atom’s center integrals are similar to that defined in Equation (13). The atom numbering is given in
Figure 5a,b. In this case, the virtual perturbation is placed on the oxygen of the hydroxyl group, which is denoted as
.
The responses on all carbons (
~
) for hexan-1-ol and hexa-1,3,5-trien-1-ol are plotted in
Figure 6a (to be complete, we present all the LRF-D values in
Tables S1–S3 in supplementary materials for hexan-1-ol, hexa-1,3,5-trien-1-ol, and
contributions of hexa-1,3,5-trien-1-ol, respectively). We can see from this figure that the response of hexan-1-ol decreases monotonically and rapidly from the nearest site to the farthest site, being consistent with the picture of the inductive effect of the saturated system. This contrasts with the response on the conjugated chain of hexa-1,3,5-trien-1-ol, which also decays from
to
but with the oscillating behavior. To analyze the behavior of the LRF-D values further, we divided the LRF-D values into
and
contributions according to the method Fias et al. used [
13]. The results are shown in
Figure 6b. This figure shows that the
contribution of the LRF-D of hexa-1,3,5-trien-1-ol is similar to that of hexan-1-ol. In particular, we found that the plus value of
of hexa-1,3,5-trien-1-ol is a result of the inductive effect mainly from the
contribution. On the other hand, being maximum at
of the
contribution obviously corresponds to the resonance picture of the
conjugated network (see
Figure 6a below), implying that LRF-D becomes an indicator of density fluctuations that are results from inductive and resonance effects of organic molecules. These results are similar to those of reference [
14], indicating that our numerical treatment is valid for our purposes.
We then evaluated the LRF-BO values of all chemical bonds on the main chain for the perturbation,
.
Figure 7a shows the LRF-BO values for the chemical bonds of the main chains of the hexan-1-ol and hexa-1,3,5-trien-1-ol (all calculated LRF-BO values are presented in
Tables S4–S6 in supplementary materials for hexan-1-ol, hexa-1,3,5-trien-1-ol, and
contributions of hexa-1,3,5-trien-1-ol, respectively). It is found from
Figure 7a that the fluctuation of bond-orders of the hexan-1-ol molecule is nearly localized in the bond between O(1) and C(2). In contrast, the profile of the LRF-BO values of hexa-1,3,5-trien-1-ol, in which points are indicated as squares, exhibits a oscillating behavior. As in the case of LRF-D values, we divide the LRF-BO values of the hexa-1,3,5-trien-1-ol into
and
contributions, which are shown in
Figure 7b. We can see from this figure that the
contribution indicated by the X points shows the behavior similar to that of the hexan-1-ol molecule shown in
Figure 7a, while the
contribution indicated by the triangular points is obviously a main cause of the oscillating behavior of the total LRF-BO values.
It should be noted that the resonance effect of the conjugate system shown in
Figure 8a is described not only with the density fluctuations on the atomic sites but also with the fluctuations of chemical bonds on the main chain. From
Figure 8a, the averages of density fluctuations and the bond fluctuations are expected to be those shown in
Figure 8b. Here + indicates the sites where the density or the bond-order increases and—the sites where the density or the bond-order decreases. We summarized the calculated LRF-D and LRF-BO values, together with those of the
contributions in parentheses, in
Figure 8c. The values in parentheses in
Figure 8c are obviously consistent with the resonance picture illustrated in
Figure 8b and the inductive effect on the charge fluctuation mainly on C(2), implying that the LRF-BO and the LRF-D complement each other, enabling us to estimate inductive and resonance effects quantitatively.
3.4. Acid Dissociation Reaction of Substituted Benzoic Acids
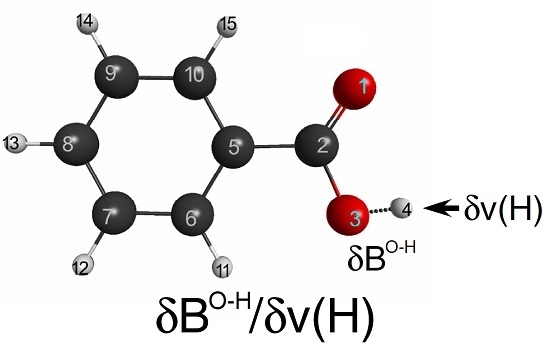
Finally, we would like to explore the applicability of LRF-BO to the acid dissociation reaction of benzoic acids. We shall focus on the response of the bond-order between the oxygen and the hydrogen atoms of the carboxylate for the virtual perturbation that is applied to each atom in the benzoic acid molecule. In
Figure 9, we listed the calculated results of the LRF-BO values,
. The response values are remarkably large for the case that the perturbation is placed on or nearby the carboxylate, in particular on O(14) and H(15) atoms of which the target O-H bond is composed, while the values become nearly zero for the perturbation that is applied to the other (phenyl) part. Not surprisingly, the absolute value of LRF-BO,
is maximum for the case, L = H(4), implying that the bond order,
, is most sensitive for the perturbation to the proton to be eliminated.
The substitution effect of benzoic acids is one of the most well-investigated topics among chemical reactions of organic molecules [
29,
30,
31]. Now we will consider dissociation reactions of non-substituted and substituted benzoic acids,
Here K
0,
and
are equilibrium constants for non-substituted, meta-substituted, and para-substituted benzoic acids, respectively. The logarithm of the ratio of the equilibrium constants is called the Hammett constant, which are defined by,
Hammett pointed out that the Hammett constant is proportional to the logarithm of the ratio of the rate constants for substituted benzoic acids [
29]. In other words, the Hammett constant determines substitution effects on both kinetics and thermodynamics for this class of systems. Note that we use two simple sets of reaction-independent substituent constants,
, rather than more complicated constants (there are more than 20 sets! see ref. [
31]), by which the researchers divided the effects and classified the types of reactions to describe the reactions in more details. This is because our intention is to lump many effects together to determine equilibrium constants of acid dissociation reactions as far as possible and to test the applicability of the LRF-BO as a descriptor for them.
Thus, we inspected the correlation between the Hammett constants and the calculated LRF-BO values of substituted benzoic acids in order to examine whether the LRF-BO could be a descriptor to cover the substitution effects. For this purpose, we picked out meta- and para-substituted benzoic acids, of which the errors of the experimentally determined Hammett constants are estimated to be within 0.1, from ref. [
30]. We exclude all the cases that a substituent group has a positive or negative charge, because, for such cases, we have to estimate LRF-BO values of hydrated clusters, of which the structures must highly fluctuate and so which are beyond the scope of our approach. First, we examined the case in which the absolute value of the LRF-BO values takes maximum, i.e., the case, L = H(4).
Figure 10a,b plot the correlations between Hammett constants and LRF-BO values for meta- and para-substituted benzoic acids, respectively. In these figures, error bars are also presented to indicate the estimated errors of the experimental data [
30]. We can see from these figures that there are linear relationships for both cases. The coefficients of determination (R
2) are calculated to be 0.772 and 0.828 for meta- and para-substituted benzoicacids, respectively. These results imply that the LRF-BO values could be useful to predict the change of the Hammett constant, i.e., p
Ka as well, for a new substituent.
When considering the reason why the linear relationships hold, it is noteworthy that
is proportional to the difference between the changes of the Gibb’s energies for the acid dissociation reactions of the non-substituted and the substituted benzoic acids, i.e.,
where
is the change of Gibb’s energies for a substituted (X-) benzoic acid and
is that for the non-substituted benzoic acid. Thus, the linear relationship between the Hammett constants and the LRF-BO values indicates that the LRF-BO is closely related to the difference of the Gibb’s free energies between the reactant state and the product state.
For completeness, we also examined the correlation between the Hammett constants and the LRF-BO values for the perturbation on each atom in benzoic acids and presented the resulting coefficients of determination in
Figure S2a,b for meta- and para-substituted benzoic acids respectively, in the
supplementary materials. Also, we listed all LRF-BO values of meta and para substituted benzoic acids in
Tables S7 and S8 respectively. Surprisingly, in some of the cases that the virtual perturbation is applied to atoms in the phenyl part, we obtained large coefficients of determination values. Nevertheless, from
Tables S7 and S8, the magnitudes of the LRF-BO values are found to be considerably small for such cases. This implies that although the bond-order between O and H in the carboxylate is remarkably sensitive to the perturbation at O(14) and H(15) in the carboxylate part, the description of substitution effects are affected by the perturbation not only of the O(14) and H(15) part, but also of the phenyl part because the induced and resonance effects work through the phenyl part. We also checked the basis set dependence of the results for 6-31G, 6-31G**, 6-31++G**, 6-311G, and 6-311++G**. See
Tables S9–S18, and Figures S3–S6. A noteworthy point is that the use of diffuse functions (
Figrues S5 and S7) deteriorates the correlation between Hammett constants and LRF-BO values. This is due to a well-known fact that the Mulliken type of population analyses often fails when the diffuse function is used [
32,
33].
As shown above, we actually found that the LRF-BO values could be useful in predicting the Hammett constants for new substitutions on the basis of the linear relationship if we use an appropriate basis set. However, we have to note that the LRF-BO values provide only rough estimations of the Hammett constants, i.e., rough estimations of the p
Ka values. In the field of computational chemistry, the estimation of p
Ka values of molecular species in various situations such as in solutions and in reaction centers of enzymes has been a hot topic. Many researchers have developed convenient and accurate methods to estimate p
Ka values [
34,
35,
36,
37,
38], and by using these methods, nowadays we would be able to estimate p
Ka values much more accurately than R
2 ~0.8 as we presented by using LRF-BO values. Our results are meaningful in another aspect, however, because the results shown in
Figure 9 and
Tables S7 and S8 are directly related to the mechanism of acid dissociation reactions: the large negative values of
indicate that a nucleophilic attack primarily induces the dissociation of the O-H bond, i.e., the acid dissociation, and the negative values of
indicate that an electrophilic effect on O(3) secondarily supports it. Although, to our knowledge, the detailed molecular mechanism of the acid dissociation of benzoic acids has not been investigated experimentally, our results are obviously reasonable from the viewpoint of chemical intuition. In addition, we would like to point out that a recent metadynamics calculation based on ab initio Car-Parinello molecular dynamics showed that the attack of water to the proton leads to form a non-dissociating meta-stable state along the reaction path (See
Figure 1a,
Figure S1, and the movie S1 [
38]), which is consistent with our results. This implies that the LRF-BO values of molecules encode essential information about the reaction mechanism of the target molecules, which is one of the most important conditions for being a good descriptor (See Introduction [
39]).