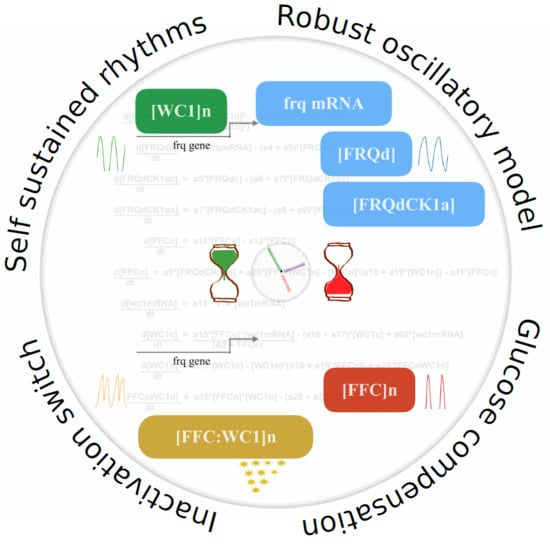
An Inactivation Switch Enables Rhythms in a Neurospora Clock Model
Abstract
:1. Introduction
2. Results
2.1. Modeling the Core Clock Elements
2.2. The Model Reproduces Self-Sustained Rhythms
2.3. Bifurcation Analysis of Our Model
2.4. Our Model Reproduced Clock Mutants
2.5. An Inactivation-Switch Allows Self-Sustained Oscillation
2.6. Sensitivity Analysis Pointed to Inherent Glucose Compensation Mechanisms
3. Discussion
4. Materials and Methods
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| N. crassa | Neurospora crassa |
| frq | Frequency gene |
| FRQ | Frequency protein |
| WCC | White Collar Complex Protein |
| WC1 | White Collar-1 Protein |
| WC2 | White Collar-2 Protein |
| wc1 | White Collar-1 gene |
| CK1a | Casein Kinase 1a |
| FRH | Frequency-interacting Helicase |
| FFC | Frequency FRH CK1a complex |
| FFCWC1 | FFC and WC1 complex |
| FWD1 | F-box/WD-40 repeat-containing protein-1 |
| CSP1 | Conidial Separation-1 |
| a.u. | arbitrary units |
| ODEs | Ordinary Differential Equations |
| N.A. | Not Applicable |
Appendix A






References
- Wever, R. Zum Mechanismus der biologischen 24-Stunden-Periodik. Kybernetik 1963, 2, 214–231. [Google Scholar]
- Konopka, R.J.; Benzer, S. Clock mutants of Drosophila melanogaster. PNAS 1971, 68, 2112–2116. [Google Scholar] [CrossRef] [PubMed]
- Dunlap, J.; Loros, J.; DeCoursey, P. Chronobiology: Biological Timekeeping; Sinauer Associates: Sunderland, MA, USA, 2004. [Google Scholar]
- Fuhr, L.; Abreu, M.; Pett, P.; Relógio, A. Circadian systems biology: When time matters. Comput. Struct. Biotechnol. J. 2015, 13, 417–426. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vanselow, K.; Vanselow, J.T.; Westermark, P.O.; Reischl, S.; Maier, B.; Korte, T.; Herrmann, A.; Herzel, H.; Schlosser, A.; Kramer, A. Differential effects of PER2 phosphorylation: Molecular basis for the human familial advanced sleep phase syndrome (FASPS). Genes Dev. 2006, 20, 2660–2672. [Google Scholar] [CrossRef] [PubMed]
- Relógio, A.; Thomas, P.; Medina-Pérez, P.; Reischl, S.; Bervoets, S.; Gloc, E.; Riemer, P.; Mang-Fatehi, S.; Maier, B.; Schäfer, R.; et al. Ras-Mediated Deregulation of the Circadian Clock in Cancer. PLoS Genet. 2014, 10, e1004338. [Google Scholar] [CrossRef] [PubMed]
- Froehlich, A.; Pregueiro, A.; Lee, K.; Denault, D. The molecular workings of the Neurospora biological clock. In Molecular Clocks and Light Signalling; John Wiley: New York, NY, USA, 2003; pp. 184–202. [Google Scholar]
- Koritala, B.; Lee, K. Natural variation of the circadian clock in Neurospora. Adv. Genet. 2017, 99, 1–37. [Google Scholar] [PubMed]
- Hurley, J.; Jankowski, M.; De los Santos, H.; Crowell, A.; Fordyce, S.; Zucker, J.; Kumar, N.; Purvine, S.; Robinson, E.; Shukla, A.; et al. Circadian proteomic analysis uncovers mechanisms of post-transcriptional regulation in metabolic pathways. Cell Syst. 2018, 7, 613–626. [Google Scholar] [CrossRef] [PubMed]
- Lakin-Thomas, P.L.; Brody, S.; Coté, G.G. Amplitude model for the effects of mutations and temperature on period and phase resetting of the Neurospora circadian oscillator. J. Biol. Rhythm. 1991, 6, 281–297. [Google Scholar] [CrossRef]
- Ruoff, P.; Rensing, L. The temperature-compensated goodwin model simulates many circadian clock properties. J. Theor. Biol. 1996, 179, 275–285. [Google Scholar] [CrossRef]
- Leloup, J.C.; Gonze, D.; Goldbeter, A. Limit Cycle Models for Circadian Rhythms Based on Transcriptional Regulation in Drosophila and Neurospora. J. Biol. Rhythm. 1999, 14, 433–448. [Google Scholar] [CrossRef]
- Ruoff, P.; Vinsjevik, M.; Monnerjahn, C.; Rensing, L. The goodwin model: Simulating the effect of light pulses on the circadian sporulation rhythm of Neurospora crassa. J. Theor. Biol. 2001, 209, 29–42. [Google Scholar] [CrossRef]
- François, P. A model for the Neurospora circadian clock. Biophys. J. 2005, 88, 2369–2383. [Google Scholar] [CrossRef] [PubMed]
- Hong, C.I.; Jolma, I.W.; Loros, J.J.; Dunlap, J.C.; Ruoff, P. Simulating dark expressions and interactions of frq and wc-1 in the Neurospora circadian clock. Biophys. J. 2008, 94, 1221–1232. [Google Scholar] [CrossRef] [PubMed]
- Dovzhenok, A.A.; Baek, M.; Lim, S.; Hong, C.I. Mathematical modeling and validation of glucose compensation of the Neurospora circadian clock. Biophys. J. 2015, 108, 1830–1839. [Google Scholar] [CrossRef] [PubMed]
- Brunner, M.; Káldi, K. Interlocked feedback loops of the circadian clock of Neurospora crassa. Mol. Microbiol. 2008, 68, 255–262. [Google Scholar] [CrossRef]
- Lee, K.; Loros, J.J.; Dunlap, J.C. Interconnected feedback loops in the Neurospora circadian system. Science 2000, 289, 107–110. [Google Scholar] [CrossRef] [PubMed]
- Merrow, M.; Brunner, M.; Roenneberg, T. Assignment of circadian function for the Neurospora clock gene frequency. Nature 1999, 399, 584. [Google Scholar] [CrossRef] [PubMed]
- Schafmeier, T.; Haase, A.; Káldi, K.; Scholz, J.; Fuchs, M.; Brunner, M. Transcriptional feedback of Neurospora circadian clock gene by phosphorylation-dependent inactivation of its transcription factor. Cell 2005, 122, 235–246. [Google Scholar] [CrossRef] [PubMed]
- He, Q.; Cha, J.; He, Q.; Lee, H.C.; Yang, Y.; Liu, Y. CKI and CKII mediate the FREQUENCY-dependent phosphorylation of the WHITE COLLAR complex to close the Neurospora circadian negative feedback loop. Genes Dev. 2006, 20, 2552–2565. [Google Scholar] [CrossRef]
- Froehlich, A.; Loros, J.; Dunlap, J. Rhythmic binding of a WHITE COLLAR-containing complex to the frequency promoter is inhibited by FREQUENCY. Proc. Natl. Acad. Sci. USA 2003, 100, 5914–5919. [Google Scholar] [CrossRef]
- Menet, J.S.; Abruzzi, K.C.; Desrochers, J.; Rodriguez, J.; Rosbash, M. Dynamic PER repression mechanisms in the Drosophila circadian clock: From on-DNA to off-DNA. Genes Dev. 2010, 24, 358–367. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.K.; Forger, D.B. A mechanism for robust circadian timekeeping via stoichiometric balance. Mol. Syst. Biol. 2012, 8, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Schafmeier, T.; Káldi, K.; Diernfellner, A.; Mohr, C.; Brunner, M. Phosphorylation-dependent maturation of Neurospora circadian clock protein from a nuclear repressor toward a cytoplasmic activator. Genes Dev. 2006, 20, 297–306. [Google Scholar] [CrossRef] [PubMed]
- Diernfellner, A.; Querfurth, C.; Salazar, C.; Höfer, T.; Brunner, M. Phosphorylation modulates rapid nucleocytoplasmic shuttling and cytoplasmic accumulation of Neurospora clock protein FRQ on a circadian time scale. Genes Dev. 2009, 23, 2192–2200. [Google Scholar] [CrossRef] [PubMed]
- Lauinger, L.; Diernfellner, A.; Falk, S.; Brunner, M. The RNA helicase FRH is an ATP-dependent regulator of CK1a in the circadian clock of Neurospora crassa. Nat. Commun. 2014, 5, 3598. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Diernfellner, A.; Schafmeier, T. Phosphorylations: Making the Neurosporacrassa circadian clock tick. FEBS Lett. 2011, 585, 1461–1466. [Google Scholar] [CrossRef] [PubMed]
- Ingalls, B. Mathematical Modeling in Systems Biology: An Introduction; MIT Press: Cambridge, MA, USA, 2013. [Google Scholar]
- Kim, J.K. Mathematical Modeling and Analysis of Cellular Clocks. Ph.D. Thesis, University of Michigan, Ann Arbor, MI, USA, 2013. [Google Scholar]
- Klipp, E.; Liebermeister, W.; Wierling, C.; Kowald, A. Systems Biology: A Textbook, 2nd ed.; Wiley-Blackwell: Hoboken, NJ, USA, 2016. [Google Scholar]
- Alon, U. An Introduction to Systems Biology: Design Principles of Biological Circuits; Chapman and Hall/CRC: Boca Raton, FL, USA, 2006. [Google Scholar]
- Sancar, G.; Sancar, C.; Brunner, M. Metabolic compensation of the Neurospora clock by a glucose-dependent feedback of the circadian repressor CSP1 on the core oscillator. Genes Dev. 2012, 26, 2435–2442. [Google Scholar] [CrossRef]
- Hughes, M.E.; DiTacchio, L.; Hayes, K.R.; Vollmers, C.; Pulivarthy, S.; Baggs, J.E.; Panda, S.; Hogenesch, J.B. Harmonics of Circadian Gene Transcription in Mammals. PLoS Genet. 2009, 5, e1000442. [Google Scholar] [CrossRef]
- Westermark, P.O.; Herzel, H. Mechanism for 12 Hr Rhythm Generation by the Circadian Clock. Cell Rep. 2013, 3, 1228–1238. [Google Scholar] [CrossRef] [Green Version]
- Ananthasubramaniam, B.; Diernfellner, A.; Brunner, M.; Herzel, H. Ultradian Rhythms in the Transcriptome of Neurospora crassa. iScience 2018, 9, 475–486. [Google Scholar] [CrossRef] [Green Version]
- Wolf, J.; Becker-Weimann, S.; Heinrich, R.; Wolf, J.; Heinrich, R. Analysing the robustness of cellular rhythms. Syst. Biol. 2005, 2, 35–41. [Google Scholar] [CrossRef]
- Schmal, C.; Leloup, J.C.; Gonze, D. Modeling and simulating the Arabidopsis thaliana circadian clock using XPP-AUTO. In Plant Circadian Networks: Methods& Protocols; Humana Press: New York, NY, USA, 2014; Volume 1158, pp. 203–208. [Google Scholar]
- Mergell, P.; Herzel, H.; Wittenberg, T.; Tigges, M.; Eysholdt, U. Phonation onset: Vocal fold modeling and high-speed glottography. J. Acoust. Soc. Am. 1998, 104, 464–470. [Google Scholar] [CrossRef]
- Steinecke, I.; Herzel, H. Bifurcations in an asymmetric vocal-fold model. J. Acoust. Soc. Am. 1995, 97, 1874–1884. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Krishna, S.; Pigolotti, S.; Mitarai, N.; Jensen, M. Switching between oscillations and homeostasis in competing negative and positive feedback motifs. J. Theor. Biol. 2012, 307, 205–210. [Google Scholar] [CrossRef] [Green Version]
- Pett, J.P.; Korencic, A.; Wesener, F.; Kramer, A.; Herzel, H. Feedback Loops of the Mammalian Circadian Clock Constitute Repressilator. PLoS Comput. Biol. 2016, 12, e1005266. [Google Scholar] [CrossRef] [PubMed]
- Pett, J.; Kondoff, M.; Bordyugov, G.; Kramer, A.; Herzel, H. Co-existing feedback loops generate tissue-specific circadian rhythms. Life Sci. Alliance 2018, 1, e201800078. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kim, J.K. Protein sequestration versus Hill-type repression in circadian clock models. IET Syst. Biol. 2016, 10, 125–135. [Google Scholar] [CrossRef]
- Korenčič, A.; Bordyugov, G.; Košir, R.; Rozman, D.; Goličnik, M.; Herzel, H. The Interplay of cis-Regulatory Elements Rules Circadian Rhythms in Mouse Liver. PLoS ONE 2012, 7, e46835. [Google Scholar] [CrossRef]
- Loros, J.J.; Dunlap, J.C. Genetic and molecular analysis of circadian rhythms in Neurospora. Annu. Rev. Physiol. 2001, 63, 757–794. [Google Scholar] [CrossRef]
- Larrondo, L.F.; Colot, H.V.; Baker, C.L.; Loros, J.J.; Dunlap, J.C. Fungal functional genomics: Tunable knockout-knock-in expression and tagging strategies. Eukaryot. Cell 2009, 8, 800–804. [Google Scholar] [CrossRef]
- Larrondo, L.F.; Olivares-Yañez, C.; Baker, C.L.; Loros, J.J.; Dunlap, J.C. Decoupling circadian clock protein turnover from circadian period determination. Science 2015, 347, 1257277. [Google Scholar] [CrossRef] [PubMed]
- Lakin-Thomas, P.L.; Coté, G.G.; Brody, S. Circadian rhythms in neurospora crassa: Biochemistry and genetics. Crit. Rev. Microbiol. 1990, 17, 365–416. [Google Scholar] [CrossRef] [PubMed]
- Tyson, J.J.; Albert, R.; Goldbeter, A.; Ruoff, P.; Sible, J. Biological switches and clocks. J. R. Soc. Interface 2008, 5, S1–S8. [Google Scholar] [CrossRef]
- Schmal, C.; Reimann, P.; Staiger, D. A Circadian Clock-Regulated Toggle Switch Explains AtGRP7 and AtGRP8 Oscillations in Arabidopsis thaliana. PLoS Comput. Biol. 2013, 9, e1002986. [Google Scholar] [CrossRef] [PubMed]
- Tyson, J.; Chen, K.; Novak, B. Sniffers, buzzers, toggles and blinkers: Dynamics of regulatory and signaling pathways in the cell. Curr. Opin. Cell Biol. 2003, 15, 221–231. [Google Scholar] [CrossRef]
- Dalchau, N.; Szép, G.; Hernansaiz-Ballesteros, R.; Barnes, C.P.; Cardelli, L.; Phillips, A.; Csikász-Nagy, A. Computing with biological switches and clocks. Nat. Comput. 2018, 17, 761–779. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hodgkin, A.L.; Huxley, A.F. A quantitative description of membrane current and its application to conduction and excitation in nerve. J. Physiol. 1952, 117, 500–544. [Google Scholar] [CrossRef]
- Hill, A.V. Proceedings supplement: The possible effects of the aggregation of the molecules of haemoglobin on its dissociation curves. J. Physiol. 1910, 40, iv–vii. [Google Scholar]
- Goldbeter, A.; Koshland, D.E. Zero-order Ultrasensitivity in Interconvertible Enzyme Systems. In Control of Metabolic Processes; Springer: Boston, MA, USA, 1990; pp. 173–182. [Google Scholar]
- Salazar, C.; Höfer, T. Multisite protein phosphorylation—From molecular mechanisms to kinetic models. FEBS J. 2009, 276, 3177–3198. [Google Scholar] [CrossRef]
- Legewie, S.; Blüthgen, N.; Herzel, H. Quantitative analysis of ultrasensitive responses. FEBS J. 2005, 272, 4071–4079. [Google Scholar] [CrossRef]
- Ferrell, J.E.; Ha, S.H. Ultrasensitivity part I: Michaelian responses and zero-order ultrasensitivity. Trends Biochem. Sci. 2014, 39, 496–503. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Legewie, S.; Blüthgen, N.; Herzel, H. Mathematical Modeling Identifies Inhibitors of Apoptosis as Mediators of Positive Feedback and Bistability. PLoS Comput. Biol. 2006, 2, e120. [Google Scholar] [CrossRef] [PubMed]
- Novak, B.; Tyson, J. Design principles of biochemical oscillators. Nat. Rev. Mol. Cell Biol. 2008, 9, 981–990. [Google Scholar] [CrossRef]
- Ferrell, J.E.; Ha, S.H. Ultrasensitivity part III: Cascades, bistable switches, and oscillators. Trends Biochem. Sci. 2014, 39, 612–618. [Google Scholar] [CrossRef] [PubMed]
- Blüthgen, N.; Legewie, S.; Herzel, H.; Kholodenko, B. Mechanisms Generating Ultrasensitivity, Bistability, and Oscillations in Signal Transduction. In Introduction to Systems Biology; Humana Press: Totowa, NJ, USA, 2007; pp. 282–299. [Google Scholar]
- Mutzel, V.; Okamoto, I.; Dunkel, I.; Saitou, M.; Giorgetti, L.; Heard, E.; Schulz, E.G. A symmetric toggle switch explains the onset of random X inactivation in different mammals. Nat. Struct. Biol. 2019, 26, 350–360. [Google Scholar] [CrossRef]
- Gérard, C.; Gonze, D.; Goldbeter, A. Revisiting a skeleton model for the mammalian cell cycle: From bistability to Cdk oscillations and cellular heterogeneity. J. Theor. Biol. 2019, 461, 276–290. [Google Scholar] [CrossRef]
- Goldbeter, A. Biochemical Oscillations and Cellular Rhythms: The Molecular Bases of Periodic and Chaotic Behaviour; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Ruoff, P.; Loros, J.J.; Dunlap, J.C. The relationship between FRQ-protein stability and temperature compensation in the Neurospora circadian clock. Proc. Natl. Acad. Sci. USA 2005, 102, 17681–17686. [Google Scholar] [CrossRef]
- Diernfellner, A.; Colot, H.V.; Dintsis, O.; Loros, J.J.; Dunlap, J.C.; Brunner, M. Long and short isoforms of Neurospora clock protein FRQ support temperature-compensated circadian rhythms. FEBS Lett. 2007, 581, 5759–5764. [Google Scholar] [CrossRef]
- François, P.; Despierre, N.; Siggia, E.D. Adaptive temperature compensation in circadian oscillations. PLoS Comput. Biol. 2012, 8, e1002585. [Google Scholar] [CrossRef]
- Dibner, C.; Sage, D.; Unser, M.; Bauer, C.; D’Eysmond, T.; Naef, F.; Schibler, U. Circadian gene expression is resilient to large fluctuations in overall transcription rates. EMBO J. 2009, 28, 123–134. [Google Scholar] [CrossRef]
- Relógio, A.; Westermark, P.O.; Wallach, T.; Schellenberg, K.; Kramer, A.; Herzel, H. Tuning the mammalian circadian clock: Robust synergy of two loops. PLoS Comput. Biol. 2011, 7, e1002309. [Google Scholar] [CrossRef] [PubMed]
- Hurley, J.M.; Larrondo, L.F.; Loros, J.J.; Dunlap, J.C. Conserved RNA helicase FRH acts nonenzymatically to support the intrinsically disordered neurospora clock protein FRQ. Mol. Cell 2013, 52, 832–843. [Google Scholar] [CrossRef] [PubMed]
- Baum, K.; Politi, A.Z.; Kofahl, B.; Steuer, R.; Wolf, J. Feedback, Mass Conservation and Reaction Kinetics Impact the Robustness of Cellular Oscillations. PLoS Comput. Biol. 2016, 12, e1005298. [Google Scholar] [CrossRef] [PubMed]
- Ruoff, P.; Vinsjevik, M.; Monnerjahn, C.; Rensing, L. The Goodwin oscillator: On the importance of degradation reactions in the circadian clock. J. Biol. Rhythm. 1999, 14, 469–479. [Google Scholar] [CrossRef] [PubMed]
- Granada, A.E.; Herzel, H.; Kramer, A.; Abraham, U. Information Transfer in the Mammalian Circadian Clock. In Information-and Communication Theory in Molecular Biology; Springer: Berlin/Heidelberg, Germany, 2018; pp. 247–257. [Google Scholar]
- Hardin, P.E.; Hall, J.C.; Rosbash, M. Feedback of the Drosophila period gene product on circadian cycling of its messenger RNA levels. Nature 1990, 343, 536–540. [Google Scholar] [CrossRef] [PubMed]
- Ananthasubramaniam, B.; Herzel, H. Positive feedback promotes oscillations in negative feedback loops. PLoS ONE 2014, 9, e104761. [Google Scholar] [CrossRef]
- Bordyugov, G.; Westermark, P.O.; Korenčič, A.; Bernard, S.; Herzel, H. Mathematical Modeling in Chronobiology. In Circadian Clocks; Springer: Berlin/Heidelberg, Germany, 2013; pp. 335–357. [Google Scholar]
- Wang, B.; Kettenbach, A.N.; Gerber, S.A.; Loros, J.J.; Dunlap, J.C. Neurospora WC-1 Recruits SWI/SNF to Remodel frequency and Initiate a Circadian Cycle. PLoS Genet. 2014, 10, e1004599. [Google Scholar] [CrossRef]
- Steffen, P.A.; Fonseca, J.P.; Ringrose, L. Epigenetics meets mathematics: Towards a quantitative understanding of chromatin biology. BioEssays 2012, 34, 901–913. [Google Scholar] [CrossRef]
- Querfurth, C.; Diernfellner, A.; Gin, E.; Malzahn, E.; Höfer, T.; Brunner, M. Circadian conformational change of the Neurospora clock protein FREQUENCY triggered by clustered hyperphosphorylation of a basic domain. Mol. Cell 2011, 43, 713–722. [Google Scholar] [CrossRef]
- Menet, J.; Rosbash, M. A new twist on clock protein phosphorylation: A conformational change leads to protein degradation. Mol. Cell 2011, 43, 695–697. [Google Scholar] [CrossRef]
- Narasimamurthy, R.; Hunt, S.; Lu, Y.; Fustin, J.; Okamura, H.; Partch, C.; Forger, D.; Kim, J.; Virshup, D. CK1δ/ϵ protein kinase primes the PER2 circadian phosphoswitch. Proc. Natl. Acad. Sci. USA 2018, 115, 5986–5991. [Google Scholar] [CrossRef] [PubMed]
- Zhou, M.; Kim, J.; Eng, G.; Forger, D.; Virshup, D. A Period2 phosphoswitch regulates and temperature compensates circadian period. Mol. Cell 2015, 60, 77–88. [Google Scholar] [CrossRef] [PubMed]
- Tyson, J.; Csikasz-Nagy, A.; Novak, B. The dynamics of cell cycle regulation. BioEssays 2002, 24, 1095–1109. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- del Olmo, M.; Kramer, A.; Herzel, H. A Robust Model for Circadian Redox Oscillations. Int. J. Mol. Sci. 2019, 20, 2368. [Google Scholar] [CrossRef] [PubMed]
- Baker, R.E.; Schnell, S.; Maini, P.K. A clock and wavefront mechanism for somite formation. Dev. Biol. 2006, 293, 116–126. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Aulehla, A.; Pourquie, O. Oscillating signaling pathways during embryonic development. Curr. Opin. Cell Biol. 2008, 20, 632–637. [Google Scholar] [CrossRef]






| Genotype (Name) | Genotype (Mutation) | Period (Race Tube) | Phenotype (Race Tube) | Core Clock Genes (Luciferase Reporter) | Temperature Compensation | Glucose Compensation | Proposed Effects Experimentally | Model Representation of Effects | References |
|---|---|---|---|---|---|---|---|---|---|
wild-type | ras1 band | 22.5 h | rhythmic | oscillate | normal | normal | [FRQ]n < [WC1]n | default parameters (a7 = 0.05, a8 = 0.34, a10 = 0.10) | [46] |
| Gly-Ser G482S | 16.5 h | rhythmic | oscillate | normal | normal | [FRQ]n of , decreased FRQ stability, and [FRQ]n > [WC1]n | faster nuclear import rate a7 = 2.5 and increased FRQ degradation rate a8 = 0.68 | [46] | |
| Gly-Asp G433D | 29 h | rhythmic | oscillate | partially lost | increased FRQ amplitude, increased FRQ stability, and approximately [FRQ]n = [WC1]n | decreased FRQ degradation rate a8 = 0.17 | [46,49] | ||
| fwd1 | COP9-signalosome | undefined | arrhythmic | oscillate | incomplete turnover of FRQ | no FFCn degradation rate a10 = 0 | [48] |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Upadhyay, A.; Brunner, M.; Herzel, H. An Inactivation Switch Enables Rhythms in a Neurospora Clock Model. Int. J. Mol. Sci. 2019, 20, 2985. https://doi.org/10.3390/ijms20122985
Upadhyay A, Brunner M, Herzel H. An Inactivation Switch Enables Rhythms in a Neurospora Clock Model. International Journal of Molecular Sciences. 2019; 20(12):2985. https://doi.org/10.3390/ijms20122985
Chicago/Turabian StyleUpadhyay, Abhishek, Michael Brunner, and Hanspeter Herzel. 2019. "An Inactivation Switch Enables Rhythms in a Neurospora Clock Model" International Journal of Molecular Sciences 20, no. 12: 2985. https://doi.org/10.3390/ijms20122985
APA StyleUpadhyay, A., Brunner, M., & Herzel, H. (2019). An Inactivation Switch Enables Rhythms in a Neurospora Clock Model. International Journal of Molecular Sciences, 20(12), 2985. https://doi.org/10.3390/ijms20122985