Quantification of Uncoupled Spin Domains in Spin-Abundant Disordered Solids
Abstract
:1. Introduction
2. Results
2.1. Characteristics of Poly(Carbon Monofluoride) Samples
2.2. Uncoupled C Enhanced CPMG MAS NMR
2.3. Signal Amplification by the Uncoupled Spin Enhanced CPMG NMR Experiment
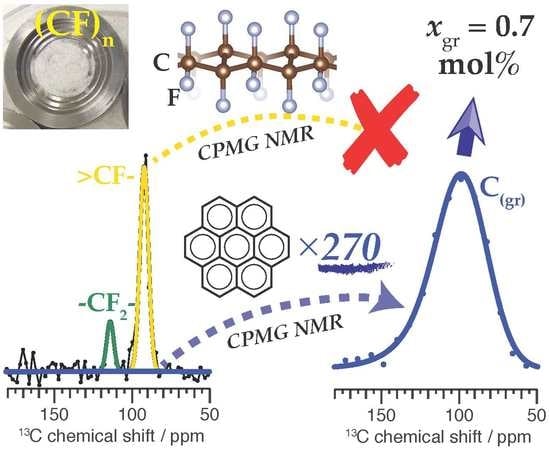
2.4. Quantification of Graphitic Carbon in Poly(Carbon Monofluoride)
3. Discussion
4. Materials and Methods
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| NMR | nuclear magnetic resonance |
| CPMG | Carr-Purcell-Meiboom-Gill |
| XRD | X-ray diffraction |
| XPS | X-ray photoelectron spectroscopy |
| SEM/EDS | scanning electron microscopy/energy dispersive X-ray spectrometry |
| MAS | magic-angle spinning |
| CP | cross-polarization |
| FID | free induction decay |
| UDEFT | Uniform Driven Equilibrium Fourier Transform |
| PIETA | phase incremented echo train acquisition |
| PC | petroleum coke |
| CB | carbon black |
| CF | carbon fiber |
| gr | graphitic carbon |
| pXRD | powder X-ray diffraction |
| S/N | signal-to-noise |
| MRE | matched reconstructed echo |
| rms | root mean square |
| dFT | discrete Fourier transform |
Appendix A. Optimized Quantitative Echo Train Reconstruction
References
- Cui, Y. A material science perspective of pharmaceutical solids. Int. J. Pharm. 2007, 339, 3–18. [Google Scholar] [CrossRef] [PubMed]
- Zhu, F.; Song, S.; Reddy, K.M.; Hirata, A.; Chen, M. Spatial heterogeneity as the structure feature for structure—Property relationship of metallic glasses. Nat. Commun. 2018, 9, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Bullard, J.W.; Jennings, H.M.; Livingston, R.A.; Nonat, A.; Scherer, G.W.; Schweitzer, J.S.; Scrivener, K.L.; Thomas, J.J. Mechanisms of cement hydration. Cem. Concr. Res. 2011, 41, 1208–1223. [Google Scholar] [CrossRef]
- Zheng, H.; Yang, R.; Liu, G.; Song, X.; Battaglia, V.S. Cooperation between Active Material, Polymeric Binder and Conductive Carbon Additive in Lithium Ion Battery Cathode. J. Phys. Chem. C 2012, 116, 4875–4882. [Google Scholar] [CrossRef]
- Newbury, D.E.; Ritchie, N.W.M. Is Scanning Electron Microscopy/Energy Dispersive X-ray Spectrometry (SEM/EDS) Quantitative? Scanning 2013, 35, 141–168. [Google Scholar] [CrossRef] [PubMed]
- Baer, D.R.; Artyushkova, K.; Richard Brundle, C.; Castle, J.E.; Engelhard, M.H.; Gaskell, K.J.; Grant, J.T.; Haasch, R.T.; Linford, M.R.; Powell, C.J.; et al. Practical guides for x-ray photoelectron spectroscopy: First steps in planning, conducting, and reporting XPS measurements. J. Vac. Sci. Technol. A 2019, 37, 031401. [Google Scholar] [CrossRef] [PubMed]
- Pines, A.; Gibby, M.G.; Waugh, J.S. Proton-enhanced NMR of dilute spins in solids. J. Chem. Phys. 1973, 59, 569–590. [Google Scholar] [CrossRef]
- Schaefer, J.; Stejskal, E.O.; Buchdahl, R. High-Resolution Carbon-13 Nuclear Magnetic Resonance Study of Some Solid, Glassy Polymers. Macromolecules 1975, 8, 291–296. [Google Scholar] [CrossRef]
- Hall, D.A.; Maus, D.C.; Gerfen, G.J.; Inati, S.J.; Becerra, L.R.; Dahlquist, F.W.; Griffin, R.G. Polarization-enhanced NMR spectroscopy of biomolecules in frozen solution. Science 1997, 276, 930–932. [Google Scholar] [CrossRef]
- Ni, Q.Z.; Daviso, E.; Can, T.V.; Markhasin, E.; Jawla, S.K.; Swager, T.M.; Temkin, R.J.; Herzfeld, J.; Griffin, R.G. High Frequency Dynamic Nuclear Polarization. Acc. Chem. Res. 2013, 46, 1933–1941. [Google Scholar] [CrossRef]
- Resing, H.A.; Garroway, A.N.; Hazlett, R.N. Determination of aromatic hydrocarbon fraction in oil shale by 13C n.m.r. with magic-angle spinning. Fuel 1978, 57, 450–454. [Google Scholar] [CrossRef]
- Hou, G.; Deng, F.; Ding, S.; Fu, R.; Yang, J.; Ye, C. Quantitative cross-polarization NMR spectroscopy in uniformly 13C-labeled solids. Chem. Phys. Lett. 2006, 421, 356–360. [Google Scholar] [CrossRef]
- Johnson, R.L.; Schmidt-Rohr, K. Quantitative solid-state 13C NMR with signal enhancement by multiple cross polarization. J. Magn. Res. 2014, 239, 44–49. [Google Scholar] [CrossRef] [PubMed]
- Meiboom, S.; Gill, D. Modified spin-echo method for measuring nuclear relaxation times. Rev. Sci. Instrum. 1958, 29, 688–691. [Google Scholar] [CrossRef] [Green Version]
- Larsen, F.H.; Jakobsen, H.J.; Ellis, P.D.; Nielsen, N.C. Sensitivity-Enhanced Quadrupolar-Echo NMR of Half-Integer Quadrupolar Nuclei. Magnitudes and Relative Orientation of Chemical Shielding and Quadrupolar Coupling Tensors. J. Phys. Chem. A 1997, 101, 8597–8606. [Google Scholar] [CrossRef]
- Larsen, F.H.; Jakobsen, H.J.; Ellis, P.D.; Nielsen, N.C. QCPMG-MAS NMR of Half-Integer Quadrupolar Nuclei. J. Magn. Res. 1998, 131, 144–147. [Google Scholar] [CrossRef] [Green Version]
- Larsen, F.H.; Farnan, I. 29Si and 17O (Q)CPMG-MAS solid-state NMR experiments as an optimum approach for half-integer nuclei having long T1 relaxation times. Chem. Phys. Lett. 2002, 357, 403–408. [Google Scholar] [CrossRef] [Green Version]
- Malfait, W.J.; Halter, W.E. Increased 29Si NMR sensitivity in glasses with a Carr–Purcell–Meiboom–Gill echotrain. J. Non-Cryst. Solids 2008, 354, 4107–4114. [Google Scholar] [CrossRef]
- Wiench, J.W.; Lin, V.S.Y.; Pruski, M. 29Si NMR in solid state with CPMG acquisition under MAS. J. Magn. Reson. 2008, 193, 233–242. [Google Scholar] [CrossRef]
- Kolyagin, Y.G.; Yakimov, A.V.; Tolborg, S.; Vennestrøm, P.N.R.; Ivanova, I.I. Application of 119Sn CPMG MAS NMR for Fast Characterization of Sn Sites in Zeolites with Natural 119Sn Isotope Abundance. J. Phys. Chem. Lett. 2016, 7, 1249–1253. [Google Scholar] [CrossRef]
- Duong, N.T.; Trébosc, J.; Lafon, O.; Amoureux, J.P. Improved sensitivity and quantification for 29Si NMR experiments on solids using UDEFT (Uniform Driven Equilibrium Fourier Transform). Solid State Nucl. Magn. Reson. 2019, 100, 52–62. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Baltisberger, J.H.; Walder, B.J.; Keeler, E.G.; Kaseman, D.C.; Sanders, K.J.; Grandinetti, P.J. Communication: Phase incremented echo train acquisition in NMR spectroscopy. J. Chem. Phys. 2012, 136, 211104. [Google Scholar] [CrossRef] [PubMed]
- Srivastava, D.J.; Baltisberger, J.H.; Florian, P.; Fayon, F.; Shakhovoy, R.A.; Deschamps, M.; Sadiki, N.; Grandinetti, P.J. Correlating structural distributions in silica glass with two-dimensional J-resolved spectroscopy. Phys. Rev. B 2018, 98, 134202. [Google Scholar] [CrossRef] [Green Version]
- Maricq, M.M.; Waugh, J.S. NMR in rotating solids. J. Chem. Phys. 1979, 70, 3300–3316. [Google Scholar] [CrossRef]
- Nakajima, T. Lithium–Graphite Fluoride Battery—History and Fundamentals. In New Fluorinated Carbons: Fundamentals and Applications; Progress in Fluorine Science; Elsevier: Amsterdam, The Netherlands, 2017; Volume 2, Chapter 13; pp. 305–323. [Google Scholar] [CrossRef]
- Panich, A.M. Nuclear magnetic resonance study of fluorine-graphite intercalation compounds and graphite fluorides. Synth. Metals 1999, 100, 169–185. [Google Scholar] [CrossRef]
- Hagaman, E.W.; Murray, D.K.; Del Cul, G.D. Solid State 13C and 19F NMR Characterization of Fluorinated Charcoal. Energy Fuels 1998, 12, 399–408. [Google Scholar] [CrossRef]
- Rüdorff, W.; Rüdorff, G. Zur Konstitution des Kohlenstoff-Monofluorids. Z. Anorg. Chem. 1947, 253, 281–296. [Google Scholar] [CrossRef]
- Hagiwara, R.; Sato, Y. Structures of Highly Fluorinated Compounds of Layered Carbon. In New Fluorinated Carbons: Fundamentals and Applications; Progress in Fluorine Science; Elsevier: Amsterdam, The Netherlands, 2017; Volume 2, Chapter 12; pp. 283–303. [Google Scholar] [CrossRef]
- Li, Z.Q.; Lu, C.J.; Xia, Z.P.; Zhou, Y.; Lou, Z. X-ray diffraction patterns of graphite and turbostratic carbon. Carbon 2007, 45, 1686–1695. [Google Scholar] [CrossRef]
- Giraudet, J.; Dubois, M.; Hamwi, A.; Stone, W.E.E.; Pirotte, P.; Masin, F. Solid-State NMR (19F and 13C) Study of Graphite Monofluoride (CF)n: 19F Spin-Lattice Magnetic Relaxation and 19F/13C Distance Determination by Hartmann-Hahn Cross Polarization. J. Phys. Chem. 2005, 109, 175–181. [Google Scholar] [CrossRef]
- Grandinetti, P.J.; Ash, J.T.; Trease, N.M. Symmetry Pathways in Solid-State NMR. Prog. Nucl. Magn. Res. Spectrosc. 2011, 59, 121–196. [Google Scholar] [CrossRef]
- Goelman, G.; Prammer, M.G. The CPMG Pulse Sequence in Strong Magnetic Field Gradients with Applications to Oil-Well Logging. J. Magn. Res. Ser. A 1995, 113, 11–18. [Google Scholar] [CrossRef]
- Song, Y.Q. Categories of Coherence Pathways for the CPMG Sequence. J. Magn. Res. 2002, 157, 82–91. [Google Scholar] [CrossRef] [PubMed]
- Bloembergen, N. On the interaction of nuclear spins in a crystalline lattice. Physica 1949, 15, 386–426. [Google Scholar] [CrossRef]
- Lowe, I.J.; Tse, D. Nuclear Spin-Lattice Relaxation via Paramagnetic Centers. Phys. Rev. 1968, 166, 279–291. [Google Scholar] [CrossRef]
- Tse, D.; Hartmann, S.R. Nuclear Spin-Lattice Relaxation via Paramagnetic Centers Without Spin Diffusion. Phys. Rev. Lett. 1968, 21, 511–514. [Google Scholar] [CrossRef]
- Phillips, J. Axiomatic theories of ideal stretched exponential relaxation (SER). J. Non Cryst. Sol. 2006, 352, 4490–4494. [Google Scholar] [CrossRef] [Green Version]
- Narayanan, A.; Hartman, J.S.; Bain, A.D. Characterizing Nonexponential Spin-Lattice Relaxation in Solid-State NMR by Fitting to the Stretched Exponential. J. Magn. Res. Ser. A 1995, 112, 58–65. [Google Scholar] [CrossRef]
- Ernst, R.; Bodenhausen, G.; Wokaun, A. Principles of Nuclear Magnetic Resonance in One and Two Dimensions; International Series of Monographs on Chemistry; Clarendon Press: Oxford, UK, 1987. [Google Scholar]
- Spencer, R.G. Equivalence of the time-domain matched filter and the spectral-domain matched filter in one-dimensional NMR spectroscopy. Concepts Magn. Reson. Part A 2010, 36A, 255–265. [Google Scholar] [CrossRef] [Green Version]
- Zhecheva, E.; Stoyanova, R.; Jiménez-Mateos, J.M.; Alcántara, R.; Lavela, P.; Tirado, J.L. EPR study on petroleum cokes annealed at different temperatures and used in lithium and sodium batteries. Carbon 2002, 40, 2301–2306. [Google Scholar] [CrossRef]
- Panich, A.M.; Shames, A.I.; Nakajima, T. On paramagnetism in fluorinated graphite: EPR and solid state NMR study; WOS:000167743000017y. J. Phys. Chem. Solids 2001, 62, 959–964. [Google Scholar] [CrossRef]
- Dubois, M.; Giraudet, J.; Guérin, K.; Hamwi, A.; Fawal, Z.; Pirotte, P.; Masin, F. EPR and Solid-State NMR Studies of Poly(dicarbon monofluoride) (C2F)n. J. Phys. Chem. B 2006, 110, 11800–11808. [Google Scholar] [CrossRef] [PubMed]
- Dong, Y.; Feng, C.; Zhao, Q.; Liang, X. Study on the Structure of C-S-H Gels of Slag–Cement Hardened Paste by 29Si, 27Al MAS NMR. Appl. Magn. Reson. 2019, 50, 1345–1357. [Google Scholar] [CrossRef]
- Foston, M.; Nunnery, G.A.; Meng, X.; Sun, Q.; Baker, F.S.; Ragauskas, A. NMR a critical tool to study the production of carbon fiber from lignin. Carbon 2013, 52, 65–73. [Google Scholar] [CrossRef]
- Harris, R.K.; Becker, E.D.; Cabral De Menezes, S.M.; Granger, P.; Hoffman, R.E.; Zilm, K.W. Further conventions for NMR shielding and chemical shifts IUPAC recommendations 2008. Sol. State Nucl. Magn. Reson. 2008, 33, 41–56. [Google Scholar] [CrossRef] [PubMed]
- Fung, B.M.; Khitrin, A.K.; Ermolaev, K. An Improved Broadband Decoupling Sequence for Liquid Crystals and Solids. J. Magn. Reson. 2000, 142, 97–101. [Google Scholar] [CrossRef] [PubMed]
- Mao, J.D.; Hu, W.G.; Schmidt-Rohr, K.; Davies, G.; Ghabbour, E.A.; Xing, B. Quantitative Characterization of Humic Substances by Solid-State Carbon-13 Nuclear Magnetic Resonance. Soil Sci. Soc. Am. J. 2000, 64, 873–884. [Google Scholar] [CrossRef]
- PhySy Ltd. RMN 1.8.6. 2018. Available online: http://physyapps.com (accessed on 1 January 2018).




| Sample | /mol% () | /mol% () |
|---|---|---|
| (CF)_gr-PC | ||
| (CF)-CB | ||
| (CF)-CF | ||
| (CF)-PC | <0.05 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Walder, B.J.; Alam, T.M. Quantification of Uncoupled Spin Domains in Spin-Abundant Disordered Solids. Int. J. Mol. Sci. 2020, 21, 3938. https://doi.org/10.3390/ijms21113938
Walder BJ, Alam TM. Quantification of Uncoupled Spin Domains in Spin-Abundant Disordered Solids. International Journal of Molecular Sciences. 2020; 21(11):3938. https://doi.org/10.3390/ijms21113938
Chicago/Turabian StyleWalder, Brennan J., and Todd M. Alam. 2020. "Quantification of Uncoupled Spin Domains in Spin-Abundant Disordered Solids" International Journal of Molecular Sciences 21, no. 11: 3938. https://doi.org/10.3390/ijms21113938
APA StyleWalder, B. J., & Alam, T. M. (2020). Quantification of Uncoupled Spin Domains in Spin-Abundant Disordered Solids. International Journal of Molecular Sciences, 21(11), 3938. https://doi.org/10.3390/ijms21113938