Ligand Binding Mechanism and Its Relationship with Conformational Changes in Adenine Riboswitch
Abstract
:1. Introduction
2. Results and Discussion
2.1. Analysis of Binding Free Energies
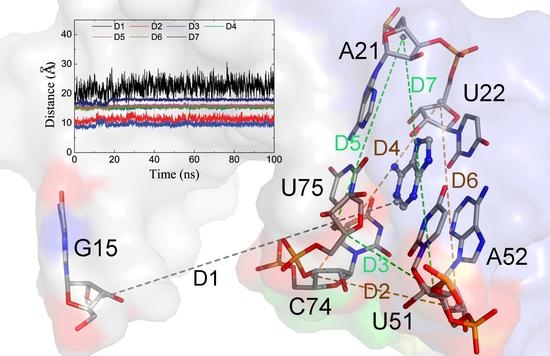
2.2. The Key Nucleotides for the Binding to Ligands
2.3. Comparison between ADE and 6AP Complexes
2.4. Comparison between 3AY and 3TT Complexes
2.5. Comparison between the Purine and Pyrimidine Analogues
2.6. The Dynamic Effects Caused by Ligand Binding
2.7. The Relationship between Conformational Change and Ligand Binding
3. Materials and Methods
3.1. System Preparation
3.2. Molecular Dynamics Simulation
3.3. Binding Free Energy Calculations
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Mandal, M.; Breaker, R.R. Gene regulation by riboswitches. Nat. Rev. Mol. Cell Biol. 2004, 5, 451–463. [Google Scholar] [CrossRef]
- Soukup, J.K.; Soukup, G.A. Riboswitches exert genetic control through metabolite-induced conformational change. Curr. Opin. Struct. Biol. 2004, 14, 344–349. [Google Scholar] [CrossRef]
- Sund, J.; Lind, C.; Aqvist, J. Binding site preorganization and ligand discrimination in the purine riboswitch. J. Phys. Chem. B 2015, 119, 773–782. [Google Scholar] [CrossRef] [PubMed]
- Priyakumar, U.D.; MacKerell, A.D., Jr. Role of the adenine ligand on the stabilization of the secondary and tertiary interactions in the adenine riboswitch. J. Mol. Biol. 2010, 396, 1422–1438. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Deigan, K.E.; Ferre-D’Amare, A.R. Riboswitches: Discovery of drugs that target bacterial gene-regulatory RNAs. Acc. Chem. Res. 2011, 44, 1329–1338. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Villa, A.; Wohnert, J.; Stock, G. Molecular dynamics simulation study of the binding of purine bases to the aptamer domain of the guanine sensing riboswitch. Nucleic Acids Res. 2009, 37, 4774–4786. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nguyen, G.T.; Scaife, M.A.; Helliwell, K.E.; Smith, A.G. Role of riboswitches in gene regulation and their potential for algal biotechnology. J. Phycol. 2016, 52, 320–328. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mandal, M.; Boese, B.; Barrick, J.E.; Winkler, W.C.; Breaker, R.R. Riboswitches control fundamental biochemical pathways in Bacillus subtilis and other bacteria. Cell 2003, 113, 577–586. [Google Scholar] [CrossRef] [Green Version]
- Mandal, M.; Breaker, R.R. Adenine riboswitches and gene activation by disruption of a transcription terminator. Nat. Struct. Mol. Biol. 2004, 11, 29–35. [Google Scholar] [CrossRef]
- Sudarsan, N.; Wickiser, J.K.; Nakamura, S.; Ebert, M.S.; Breaker, R.R. An mRNA structure in bacteria that controls gene expression by binding lysine. Genes Dev. 2003, 17, 2688–2697. [Google Scholar] [CrossRef] [Green Version]
- Mandal, M.; Lee, M.; Barrick, J.E.; Weinberg, Z.; Emilsson, G.M.; Ruzzo, W.L.; Breaker, R.R. A glycine-dependent riboswitch that uses cooperative binding to control gene expression. Science 2004, 306, 275–279. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Serganov, A.; Huang, L.; Patel, D.J. Coenzyme recognition and gene regulation by a flavin mononucleotide riboswitch. Nature 2009, 458, 233–237. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Barrick, J.E.; Breaker, R.R. The distributions, mechanisms, and structures of metabolite-binding riboswitches. Genome Biol. 2007, 8, R239. [Google Scholar] [CrossRef] [Green Version]
- Dann, C.E., 3rd; Wakeman, C.A.; Sieling, C.L.; Baker, S.C.; Irnov, I.; Winkler, W.C. Structure and mechanism of a metal-sensing regulatory RNA. Cell 2007, 130, 878–892. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Serganov, A.; Yuan, Y.R.; Pikovskaya, O.; Polonskaia, A.; Malinina, L.; Phan, A.T.; Hobartner, C.; Micura, R.; Breaker, R.R.; Patel, D.J. Structural basis for discriminative regulation of gene expression by adenine- and guanine-sensing mRNAs. Chem. Biol. 2004, 11, 1729–1741. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gilbert, S.D.; Mediatore, S.J.; Batey, R.T. Modified pyrimidines specifically bind the purine riboswitch. J. Am. Chem. Soc. 2006, 128, 14214–14215. [Google Scholar] [CrossRef] [PubMed]
- Hu, G.; Ma, A.; Wang, J. Ligand Selectivity Mechanism and Conformational Changes in Guanine Riboswitch by Molecular Dynamics Simulations and Free Energy Calculations. J. Chem. Inf. Model. 2017, 57, 918–928. [Google Scholar] [CrossRef]
- Stoddard, C.D.; Gilbert, S.D.; Batey, R.T. Ligand-dependent folding of the three-way junction in the purine riboswitch. RNA 2008, 14, 675–684. [Google Scholar] [CrossRef] [Green Version]
- Gilbert, S.D.; Reyes, F.E.; Edwards, A.L.; Batey, R.T. Adaptive ligand binding by the purine riboswitch in the recognition of guanine and adenine analogs. Structure 2009, 17, 857–868. [Google Scholar] [CrossRef] [Green Version]
- Batey, R.T.; Gilbert, S.D.; Montange, R.K. Structure of a natural guanine-responsive riboswitch complexed with the metabolite hypoxanthine. Nature 2004, 432, 411–415. [Google Scholar] [CrossRef]
- Ling, B.; Wang, Z.; Zhang, R.; Meng, X.; Liu, Y.; Zhang, C.; Liu, C. Theoretical studies on the interaction of modified pyrimidines and purines with purine riboswitch. J. Mol. Graph. Model. 2009, 28, 37–45. [Google Scholar] [CrossRef] [PubMed]
- Ling, B.; Zhang, R.; Wang, Z.; Dong, L.; Liu, Y.; Zhang, C.; Liu, C. Theoretical studies on the interaction of guanine riboswitch with guanine and its closest analogues. Mol. Simulat. 2010, 36, 929–938. [Google Scholar] [CrossRef]
- Noeske, J.; Buck, J.; Furtig, B.; Nasiri, H.R.; Schwalbe, H.; Wohnert, J. Interplay of ’induced fit’ and preorganization in the ligand induced folding of the aptamer domain of the guanine binding riboswitch. Nucleic Acids Res. 2007, 35, 572–583. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Howe, J.A.; Wang, H.; Fischmann, T.O.; Balibar, C.J.; Xiao, L.; Galgoci, A.M.; Malinverni, J.C.; Mayhood, T.; Villafania, A.; Nahvi, A.; et al. Selective small-molecule inhibition of an RNA structural element. Nature 2015, 526, 672–677. [Google Scholar] [CrossRef] [PubMed]
- Brenner, M.D.; Scanlan, M.S.; Nahas, M.K.; Ha, T.; Silverman, S.K. Multivector fluorescence analysis of the xpt guanine riboswitch aptamer domain and the conformational role of guanine. Biochemistry 2010, 49, 1596–1605. [Google Scholar] [CrossRef]
- Gilbert, S.D.; Stoddard, C.D.; Wise, S.J.; Batey, R.T. Thermodynamic and kinetic characterization of ligand binding to the purine riboswitch aptamer domain. J. Mol. Biol. 2006, 359, 754–768. [Google Scholar] [CrossRef]
- Buck, J.; Furtig, B.; Noeske, J.; Wohnert, J.; Schwalbe, H. Time-resolved NMR methods resolving ligand-induced RNA folding at atomic resolution. Proc. Natl. Acad. Sci. USA 2007, 104, 15699–15704. [Google Scholar] [CrossRef] [Green Version]
- Stagno, J.R.; Liu, Y.; Bhandari, Y.R.; Conrad, C.E.; Panja, S.; Swain, M.; Fan, L.; Nelson, G.; Li, C.; Wendel, D.R.; et al. Structures of riboswitch RNA reaction states by mix-and-inject XFEL serial crystallography. Nature 2017, 541, 242–246. [Google Scholar] [CrossRef]
- Liu, N.; Zhou, W.; Guo, Y.; Wang, J.; Fu, W.; Sun, H.; Li, D.; Duan, M.; Hou, T. Molecular Dynamics Simulations Revealed the Regulation of Ligands to the Interactions between Androgen Receptor and Its Coactivator. J. Chem. Inf. Model. 2018, 58, 1652–1661. [Google Scholar] [CrossRef]
- Di Palma, F.; Colizzi, F.; Bussi, G. Ligand-induced stabilization of the aptamer terminal helix in the add adenine riboswitch. RNA 2013, 19, 1517–1524. [Google Scholar] [CrossRef] [Green Version]
- Allner, O.; Nilsson, L.; Villa, A. Loop-loop interaction in an adenine-sensing riboswitch: A molecular dynamics study. RNA 2013, 19, 916–926. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Whitford, P.C.; Schug, A.; Saunders, J.; Hennelly, S.P.; Onuchic, J.N.; Sanbonmatsu, K.Y. Nonlocal helix formation is key to understanding S-adenosylmethionine-1 riboswitch function. Biophys. J. 2009, 96, L7–L9. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ogrizek, M.; Konc, J.; Bren, U.; Hodoscek, M.; Janezic, D. Role of magnesium ions in the reaction mechanism at the interface between Tm1631 protein and its DNA ligand. Chem. Cent. J. 2016, 10, 41. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sharma, M.; Bulusu, G.; Mitra, A. MD simulations of ligand-bound and ligand-free aptamer: Molecular level insights into the binding and switching mechanism of the add A-riboswitch. RNA 2009, 15, 1673–1692. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, W.; Wang, W.; Takada, S. Energy landscape views for interplays among folding, binding, and allostery of calmodulin domains. Proc. Natl. Acad. Sci. USA 2014, 111, 10550–10555. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shen, J.; Tan, C.; Zhang, Y.; Li, X.; Li, W.; Huang, J.; Shen, X.; Tang, Y. Discovery of potent ligands for estrogen receptor beta by structure-based virtual screening. J. Med. Chem. 2010, 53, 5361–5365. [Google Scholar] [CrossRef]
- Hu, G.; Wang, J. Ligand selectivity of estrogen receptors by a molecular dynamics study. Eur. J. Med. Chem. 2014, 74, 726–735. [Google Scholar] [CrossRef]
- Chen, J.; Wang, J.; Zhu, W.; Li, G. A computational analysis of binding modes and conformation changes of MDM2 induced by p53 and inhibitor bindings. J. Comput. Aided Mol. Des. 2013, 27, 965–974. [Google Scholar] [CrossRef]
- Gouda, H.; Kuntz, I.D.; Case, D.A.; Kollman, P.A. Free energy calculations for theophylline binding to an RNA aptamer: Comparison of MM-PBSA and thermodynamic integration methods. Biopolymers 2003, 68, 16–34. [Google Scholar] [CrossRef]
- Journal of Molecular BiologyKormos, B.L.; Benitex, Y.; Baranger, A.M.; Beveridge, D.L. Affinity and specificity of protein U1A-RNA complex formation based on an additive component free energy model. J. Mol. Biol. 2007, 371, 1405–1419. [Google Scholar] [CrossRef] [Green Version]
- Reyes, C.M.; Kollman, P.A. Structure and thermodynamics of RNA-protein binding: Using molecular dynamics and free energy analyses to calculate the free energies of binding and conformational change. J. Mol. Biol. 2000, 297, 1145–1158. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, J.; Wang, X.; Pang, L.; Zhang, J.Z.H.; Zhu, T. Effect of mutations on binding of ligands to guanine riboswitch probed by free energy perturbation and molecular dynamics simulations. Nucleic Acids Res. 2019, 47, 6618–6631. [Google Scholar] [CrossRef] [PubMed]
- Jorgensen, W.L.; Thomas, L.L. Perspective on Free-Energy Perturbation Calculations for Chemical Equilibria. J. Chem. Theory Comput. 2008, 4, 869–876. [Google Scholar] [CrossRef] [Green Version]
- Kästner, J. Umbrella sampling. Wiley Interdisciplinary Reviews: Computational Molecular Science 2011, 1, 932–942. [Google Scholar] [CrossRef]
- Wang, C.; Greene, D.; Xiao, L.; Qi, R.; Luo, R. Recent Developments and Applications of the MMPBSA Method. Front. Mol. Biosci. 2017, 4, 87. [Google Scholar] [CrossRef] [Green Version]
- Hu, G.; Ma, A.; Dou, X.; Zhao, L.; Wang, J. Computational studies of a mechanism for binding and drug resistance in the wild type and four mutations of HIV-1 protease with a GRL-0519 inhibitor. Int. J. Mol. Sci. 2016, 17, 819. [Google Scholar] [CrossRef] [Green Version]
- Stoica, I.; Sadiq, S.K.; Coveney, P.V. Rapid and accurate prediction of binding free energies for saquinavir-bound HIV-1 proteases. J. Am. Chem. Soc. 2008, 130, 2639–2648. [Google Scholar] [CrossRef]
- Fulle, S.; Gohlke, H. Molecular recognition of RNA: Challenges for modelling interactions and plasticity. J. Mol. Recognit. 2010, 23, 220–231. [Google Scholar] [CrossRef]
- Jin, Y.; Duan, M.; Wang, X.; Kong, X.; Zhou, W.; Sun, H.; Liu, H.; Li, D.; Yu, H.; Li, Y.; et al. Communication between the Ligand-Binding Pocket and the Activation Function-2 Domain of Androgen Receptor Revealed by Molecular Dynamics Simulations. J. Chem. Inf. Model. 2019, 59, 842–857. [Google Scholar] [CrossRef]
- Yang, Y.; Shen, Y.; Liu, H.; Yao, X. Molecular dynamics simulation and free energy calculation studies of the binding mechanism of allosteric inhibitors with p38alpha MAP kinase. J. Chem. Inf. Model. 2011, 51, 3235–3246. [Google Scholar] [CrossRef]
- Wang, E.; Sun, H.; Wang, J.; Wang, Z.; Liu, H.; Zhang, J.Z.H.; Hou, T. End-Point Binding Free Energy Calculation with MM/PBSA and MM/GBSA: Strategies and Applications in Drug Design. Chem. Rev. 2019, 119, 9478–9508. [Google Scholar] [CrossRef] [PubMed]
- Gohlke, H.; Kiel, C.; Case, D.A. Insights into protein–protein binding by binding free energy calculation and free energy decomposition for the Ras–Raf and Ras–RalGDS complexes. J. Mol. Biol. 2003, 330, 891–913. [Google Scholar] [CrossRef]
- Bos, F.; Pleiss, J. Multiple molecular dynamics simulations of TEM beta-lactamase: Dynamics and water binding of the omega-loop. Biophys. J. 2009, 97, 2550–2558. [Google Scholar] [CrossRef] [Green Version]
- Connelly, C.M.; Numata, T.; Boer, R.E.; Moon, M.H.; Sinniah, R.S.; Barchi, J.J.; Ferre-D’Amare, A.R.; Schneekloth, J.S., Jr. Synthetic ligands for PreQ1 riboswitches provide structural and mechanistic insights into targeting RNA tertiary structure. Nat. Commun. 2019, 10, 1501. [Google Scholar] [CrossRef]
- Rizvi, N.F.; Howe, J.A.; Nahvi, A.; Klein, D.J.; Fischmann, T.O.; Kim, H.-Y.; McCoy, M.A.; Walker, S.S.; Hruza, A.; Richards, M.P.; et al. Discovery of Selective RNA-Binding Small Molecules by Affinity-Selection Mass Spectrometry. ACS Chem. Biol. 2018, 13, 820–831. [Google Scholar] [CrossRef] [PubMed]
- Jorgensen, W.L.; Chandrasekhar, J.; Madura, J.D.; Impey, R.W.; Klein, M.L. Comparison of simple potential functions for simulating liquid water. J. Comput. Phys. 1983, 79, 926–935. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Montgomery, J.A., Jr.; Vreven, T.; Kudin, K.N.; Burant, J.C.; et al. Gaussian 03, Revision C.02; Gaussian, Inc.: Wallingford, UK, 2004. [Google Scholar] [CrossRef]
- Bayly, C.I.; Cieplak, P.; Cornell, W.; Kollman, P.A. A well-behaved electrostatic potential based method using charge restraints for deriving atomic charges: The RESP model. J. Phys. Chem. 1993, 97, 10269–10280. [Google Scholar] [CrossRef]
- Wang, J.; Wolf, R.M.; Caldwell, J.W.; Kollman, P.A.; Case, D.A. Development and testing of a general amber force field. J. Comput. Chem. 2004, 25, 1157–1174. [Google Scholar] [CrossRef] [PubMed]
- Zgarbova, M.; Otyepka, M.; Sponer, J.; Mladek, A.; Banas, P.; Cheatham, T.E., 3rd; Jurecka, P. Refinement of the Cornell et al. Nucleic Acids Force Field Based on Reference Quantum Chemical Calculations of Glycosidic Torsion Profiles. J. Chem. Theory Comput. 2011, 7, 2886–2902. [Google Scholar] [CrossRef]
- Case, D.A.; Darden, T.A.; Cheatham, T.E., III; Simmerling, C.L.; Wang, J.; Duke, R.E.; Luo, R.; Walker, R.C.; Zhang, W.; Merz, K.M.; et al. Amber 12; University of California: San Francisco, CA, USA, 2012. [Google Scholar]
- Ryckaert, J.P.; Ciccotti, G.; Berendsen, H.J.C. Numerical-integration of cartesian equations of motion of a system with constraints - molecular-dynamics of N-Alkanes. J. Comput. Phys. 1977, 23, 327–341. [Google Scholar] [CrossRef] [Green Version]
- Darden, T.; York, D.; Pedersen, L. Particle mesh ewald -and.Log(N) method for ewald sums in large systems. J. Comput. Phys. 1993, 98, 10089–10092. [Google Scholar]
- Hu, G.; Cao, Z.; Xu, S.; Wang, W.; Wang, J. Revealing the binding modes and the unbinding of 14-3-3sigma proteins and inhibitors by computational methods. Sci. Rep. 2015, 5, 16481. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, J.; Wang, X.; Zhu, T.; Zhang, Q.; Zhang, J.Z. A Comparative Insight into Amprenavir Resistance of Mutations V32I, G48V, I50V, I54V, and I84V in HIV-1 Protease Based on Thermodynamic Integration and MM-PBSA Methods. J. Chem. Inf. Model. 2015, 55, 1903–1913. [Google Scholar] [CrossRef] [PubMed]
- Onufriev, A.; Bashford, D.; Case, D.A. Exploring protein native states and large-scale conformational changes with a modified generalized born model. Proteins 2004, 55, 383–394. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Case, D.A. Normal mode analysis of protein dynamics. Curr. Opin. Struct. Biol. 1994, 4, 285–290. [Google Scholar] [CrossRef]







| Items b | ADE | 6AP | 3AY | 3TT | 2DY | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| GR(C74U) | AR | GR(C74U) | AR | GR(C74U) | AR | GR(C74U) | AR | GR(C74U) | AR | |
| −31.48 ± 0.45 | −31.67 ± 0.61 | −34.35 ± 0.90 | −36.87 ± 0.89 | −30.77 ± 0.76 | −29.49 ± 0.55 | −32.23 ± 1.09 | −32.10 ± 0.49 | −25.57 ± 1.49 | −24.71 ± 1.13 | |
| −25.45 ± 0.28 | −25.98 ± 0.40 | −27.56 ± 0.32 | −27.49 ± 0.38 | −23.55 ± 0.42 | −23.21 ± 0.47 | −22.90 ± 0.48 | −22.48 ± 0.54 | −20.93 ± 0.44 | −20.43 ± 0.44 | |
| 1.42 ± 0.02 | 1.48 ± 0.02 | 1.39 ± 0.02 | 1.50 ± 0.02 | 1.39 ± 0.02 | 1.48 ± 0.02 | 1.40 ± 0.01 | 1.45 ± 0.02 | 1.37 ± 0.02 | 1.51 ± 0.02 | |
| −2.86 ± 0.02 | −2.84 ± 0.02 | −3.01 ± 0.02 | −3.00 ± 0.02 | −2.81 ± 0.01 | −2.81 ± 0.01 | −2.75 ± 0.02 | −2.76 ± 0.01 | −2.70 ± 0.01 | −2.73 ± 0.01 | |
| 35.54 ± 0.72 | 33.64 ± 0.91 | 36.35 ± 0.01 | 36.45 ± 0.01 | 34.63 ± 1.41 | 32.31 ± 1.17 | 34.88 ± 1.50 | 32.89 ± 1.06 | 29.52 ± 1.55 | 28.74 ± 0.87 | |
| 4.06 ± 0.46 | 1.97 ± 0.43 | 2.00 ± 1.15 | −0.42 ± 0.89 | 3.85 ± 1.25 | 2.81 ± 1.17 | 2.66 ± 1.60 | 0.80 ± 1.13 | 3.96 ± 1.23 | 4.03 ± 0.93 | |
| −28.30 ± 0.28 | −28.83 ± 0.39 | −30.57 ± 0.65 | −30.48 ± 0.18 | −26.36 ± 0.42 | −26.01 ± 0.47 | −25.64 ± 0.47 | −25.23 ± 0.54 | −23.63 ± 0.43 | −23.17 ± 0.43 | |
| −22.83 ± 0.62 | −25.38 ± 0.57 | −27.18 ± 0.31 | −29.40 ± 0.38 | −21.12 ± 1.42 | −21.72 ± 1.18 | −21.59 ± 1.90 | −22.98 ± 1.18 | −18.31 ± 1.06 | −17.63 ± 1.10 | |
| −13.31 ± 0.24 | −13.62 ± 0.31 | −14.58 ± 0.79 | −14.03 ± 0.46 | −14.69 ± 0.33 | −14.46 ± 0.28 | −15.29 ± 0.20 | −15.30 ± 0.22 | −13.72 ± 0.25 | −13.22 ± 0.22 | |
| −9.53 ± 0.73 | −11.76 ± 0.41 | −12.60 ± 0.40 | −15.37 ± 0.31 | −6.42 ± 1.55 | −7.27 ± 0.98 | −6.30 ± 1.86 | −7.68 ± 1.10 | −4.58 ± 1.21 | −4.41 ± 1.14 | |
| c | −8.78 (−8.8) | −9.20 (−9.2) | −10.57 (−11) | −11.53 (−12) | −6.45 (−6.6) | −7.82 (−7.8) | −6.45 (−6.5) | null | null | null |
| Items | ADE | 6AP | 3AY | 3TT | 2DY |
|---|---|---|---|---|---|
| GR(C74U) | 1.03 ± 0.37 | 1.27 ± 0.32 | 1.41 ± 0.58 | 1.23 ± 0.35 | 1.49 ± 0.46 |
| AR | 1.12 ± 0.33 | 1.04 ± 0.24 | 1.41 ± 0.39 | 1.32 ± 0.33 | 1.34 ± 0.46 |
| Items | GR(C74U) | AR | ||||
|---|---|---|---|---|---|---|
| Open | Closed | Distance a | Open | Closed | Distance a | |
| ADE | 19.82% | 43.22% | 10.08 | 19.82% | 43.22% | 10.08 |
| 6AP | 18.33% | 48.49% | 10.00 | 23.83% | 39.74% | 10.07 |
| 3AY | 19.44% | 49.12% | 10.25 | 15.88% | 52.27% | 10.14 |
| 3TT | 11.76% | 56.64% | 9.89 | 13.26% | 55.36% | 10.06 |
| 2DY | 18.69% | 46.28% | 10.38 | 28.23% | 35.44% | 10.59 |
| Rb | 0.66 | −0.56 | 0.72 | −0.62 | ||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, G.; Li, H.; Xu, S.; Wang, J. Ligand Binding Mechanism and Its Relationship with Conformational Changes in Adenine Riboswitch. Int. J. Mol. Sci. 2020, 21, 1926. https://doi.org/10.3390/ijms21061926
Hu G, Li H, Xu S, Wang J. Ligand Binding Mechanism and Its Relationship with Conformational Changes in Adenine Riboswitch. International Journal of Molecular Sciences. 2020; 21(6):1926. https://doi.org/10.3390/ijms21061926
Chicago/Turabian StyleHu, Guodong, Haiyan Li, Shicai Xu, and Jihua Wang. 2020. "Ligand Binding Mechanism and Its Relationship with Conformational Changes in Adenine Riboswitch" International Journal of Molecular Sciences 21, no. 6: 1926. https://doi.org/10.3390/ijms21061926
APA StyleHu, G., Li, H., Xu, S., & Wang, J. (2020). Ligand Binding Mechanism and Its Relationship with Conformational Changes in Adenine Riboswitch. International Journal of Molecular Sciences, 21(6), 1926. https://doi.org/10.3390/ijms21061926