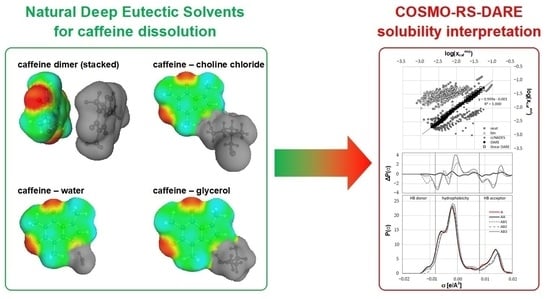
Quantification of Caffeine Interactions in Choline Chloride Natural Deep Eutectic Solvents: Solubility Measurements and COSMO-RS-DARE Interpretation
Abstract
:1. Introduction
2. Results and Discussion
2.1. Solid State Characteristics
2.2. Experimental Solubility of Caffeine
2.3. Intermolecular Interactions of Caffeine with Solvents Components
2.4. Results of COSMO-DARE Computations
2.5. Role of Fusion Data in Solubility Model
3. Materials and Methods
3.1. Materials
3.2. Preparation of the Calibration Curve
3.3. Preparation of Samples in NADES and Their Mixtures with Water
3.4. Solubility Measurements
3.5. FTIR-ATR Measurements
3.6. Differential Scanning Calorimetry Measurements
3.7. Affinities and Intermolecular Interactions
3.8. Solubility Computations
3.9. COSMO-RS DARE and Metafiles
3.10. Contacts Conformational Analysis
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ashihara, H.; Mizuno, K.; Yokota, T.; Crozier, A. Xanthine Alkaloids: Occurrence, Biosynthesis, and Function in Plants. Prog. Chem. Org. Nat. Prod. 2017, 105, 1–88. [Google Scholar] [PubMed]
- Ashihara, H.; Sano, H.; Crozier, A. Caffeine and related purine alkaloids: Biosynthesis, catabolism, function and genetic engineering. Phytochemistry 2008, 69, 841–856. [Google Scholar] [CrossRef] [PubMed]
- Jouyban, A. Handbook of Solubility Data for Pharmaceuticals, 1st ed.; CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar]
- Hansch, C.; Leo, A.; Hoekman, D. Exploring QSAR: Volume 2: Hydrophobic, Electronic, and Steric Constants, 1st ed.; American Chemical Society: Washington, WA, USA, 1995. [Google Scholar]
- Wang, X.; Zhang, H.; Wei, Y.; Bao, L.; Liu, S.; Yuan, S.; Yuan, S. Effect of pH on caffeine removal from aqueous media by graphene/graphene oxide adsorption. Colloids Surf. A Physicochem. Eng. Asp. 2022, 644, 128864. [Google Scholar] [CrossRef]
- Heckman, M.A.; Weil, J.; de Mejia, E.G. Caffeine (1,3,7-trimethylxanthine) in Foods: A Comprehensive Review on Consumption, Functionality, Safety, and Regulatory Matters. J. Food Sci. 2010, 75, R77–R87. [Google Scholar] [CrossRef]
- Fredholm, B.B. Notes on the History of Caffeine Use. Handb. Exp. Pharmacol. 2011, 200, 1–9. [Google Scholar]
- Lu, H.; Zhang, J.; Yang, Y.; Yang, X.; Xu, B.; Yang, W.; Tong, T.; Jin, S.; Shen, C.; Rao, H.; et al. Earliest tea as evidence for one branch of the Silk Road across the Tibetan Plateau. Sci. Rep. 2016, 6, 18955. [Google Scholar] [CrossRef] [Green Version]
- Patel, M.; Kumar, R.; Kishor, K.; Mlsna, T.; Pittman, C.U.; Mohan, D. Pharmaceuticals of Emerging Concern in Aquatic Systems: Chemistry, Occurrence, Effects, and Removal Methods. Chem. Rev. 2019, 119, 3510–3673. [Google Scholar] [CrossRef] [Green Version]
- Lin, P.; Liang, Z.; Wang, M. Caffeine consumption and mortality in populations with different weight statuses: An analysis of NHANES 1999–2014. Nutrition 2022, 102, 111731. [Google Scholar] [CrossRef]
- Prado, E.; Magalhães-Neto, A.; Neto, J.R.; Bassini, A.; Cameron, L.C. Caffeine decreases ammonemia in athletes using a ketogenic diet during prolonged exercise. Nutrition 2021, 91–92, 111377. [Google Scholar] [CrossRef]
- Sainz, I.; Collado-Mateo, D.; Coso, J. Del Effect of acute caffeine intake on hit accuracy and reaction time in professional e-sports players. Physiol. Behav. 2020, 224, 113031. [Google Scholar] [CrossRef]
- Laatar, R.; Ben Waer, F.; Rebai, H.; Sahli, S. Caffeine consumption improves motor and cognitive performances during dual tasking in middle-aged women. Behav. Brain Res. 2021, 412, 113437. [Google Scholar] [CrossRef] [PubMed]
- Al Ammar, W.A.; Albeesh, F.H.; Khattab, R.Y. Food and Mood: The Corresponsive Effect. Curr. Nutr. Rep. 2020, 9, 296–308. [Google Scholar] [CrossRef] [PubMed]
- Hlais, S.; Francis, R.; Jneid, S.; Aoun, A. MON-PO632: The Prevalence, Contributing Factors and Side Effects of Caffeine Consumption Among Lebanese University Medical and Pharmacy Students. Clin. Nutr. 2019, 38, S293. [Google Scholar] [CrossRef]
- Temple, J.L. Review: Trends, Safety, and Recommendations for Caffeine Use in Children and Adolescents. J. Am. Acad. Child Adolesc. Psychiatry 2019, 58, 36–45. [Google Scholar] [CrossRef] [Green Version]
- Temple, J.L.; Bernard, C.; Lipshultz, S.E.; Czachor, J.D.; Westphal, J.A.; Mestre, M.A. The Safety of Ingested Caffeine: A Comprehensive Review. Front. Psychiatry 2017, 8, 80. [Google Scholar] [CrossRef] [Green Version]
- Fisone, G.; Borgkvist, A.; Usiello, A. Caffeine as a psychomotor stimulant: Mechanism of action. Cell. Mol. Life Sci. 2004, 61, 857–872. [Google Scholar] [CrossRef]
- Faber, M.S.; Jetter, A.; Fuhr, U. Assessment of CYP1A2 Activity in Clinical Practice: Why, How, and When? Basic Clin. Pharmacol. Toxicol. 2005, 97, 125–134. [Google Scholar] [CrossRef]
- Aboumanei, M.H.; Mahmoud, A.F. Design and development of a proniosomal transdermal drug delivery system of caffeine for management of migraine: In vitro characterization, 131I-radiolabeling and in vivo biodistribution studies. Process Biochem. 2020, 97, 201–212. [Google Scholar] [CrossRef]
- Ghelardini, C.; Galeotti, N.; Grazioli, I.; Uslenghi, C. Indomethacin, alone and combined with prochlorperazine and caffeine, but not sumatriptan, abolishes peripheral and central sensitization in in vivo models of migraine. J. Pain 2004, 5, 413–419. [Google Scholar] [CrossRef]
- Santoro, K.L.; Yakah, W.; Singh, P.; Ramiro-Cortijo, D.; Medina-Morales, E.; Freedman, S.D.; Martin, C.R. Acetaminophen and Xenobiotic Metabolites in Human Milk and the Development of Bronchopulmonary Dysplasia and Retinopathy of Prematurity in a Cohort of Extremely Preterm Infants. J. Pediatr. 2022, 244, 224–229. [Google Scholar] [CrossRef]
- Gibbons, C.H.; Schmidt, P.; Biaggioni, I.; Frazier-Mills, C.; Freeman, R.; Isaacson, S.; Karabin, B.; Kuritzky, L.; Lew, M.; Low, P.; et al. The recommendations of a consensus panel for the screening, diagnosis, and treatment of neurogenic orthostatic hypotension and associated supine hypertension. J. Neurol. 2017, 264, 1567–1582. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Armanian, A.M.; Iranpour, R.; Faghihian, E.; Salehimehr, N. Caffeine Administration to Prevent Apnea in Very Premature Infants. Pediatr. Neonatol. 2016, 57, 408–412. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Göke, K.; Lorenz, T.; Repanas, A.; Schneider, F.; Steiner, D.; Baumann, K.; Bunjes, H.; Dietzel, A.; Finke, J.H.; Glasmacher, B.; et al. Novel strategies for the formulation and processing of poorly water-soluble drugs. Eur. J. Pharm. Biopharm. 2018, 126, 40–56. [Google Scholar] [CrossRef] [PubMed]
- Takagi, T.; Ramachandran, C.; Bermejo, M.; Yamashita, S.; Yu, L.X.; Amidon, G.L. A provisional biopharmaceutical classification of the top 200 oral drug products in the United States, Great Britain, Spain, and Japan. Mol. Pharm. 2006, 3, 631–643. [Google Scholar] [CrossRef]
- Ku, M.S.; Dulin, W. A biopharmaceutical classification-based Right-First-Time formulation approach to reduce human pharmacokinetic variability and project cycle time from First-In-Human to clinical Proof-Of-Concept. Pharm. Dev. Technol. 2012, 17, 285–302. [Google Scholar] [CrossRef]
- Zhang, W.; Zhao, Y.; Xu, L.; Song, X.; Yuan, X.; Sun, J.; Zhang, J. Superfine grinding induced amorphization and increased solubility of α-chitin. Carbohydr. Polym. 2020, 237, 116145. [Google Scholar] [CrossRef]
- Auch, C.; Jede, C.; Harms, M.; Wagner, C.; Mäder, K. Impact of amorphization and GI physiology on supersaturation and precipitation of poorly soluble weakly basic drugs using a small-scale in vitro transfer model. Int. J. Pharm. 2020, 574, 118917. [Google Scholar] [CrossRef]
- Prajapati, H.; Serajuddin, A.T.M. Development of Fully Redispersible Dried Nanocrystals by Using Sucrose Laurate as Stabilizer for Increasing Surface Area and Dissolution Rate of Poorly Water-Soluble Drugs. J. Pharm. Sci. 2022, 111, 780–793. [Google Scholar] [CrossRef]
- Lopez-Vidal, L.; Real, J.P.; Real, D.A.; Camacho, N.; Kogan, M.J.; Paredes, A.J.; Palma, S.D. Nanocrystal-based 3D-printed tablets: Semi-solid extrusion using melting solidification printing process (MESO-PP) for oral administration of poorly soluble drugs. Int. J. Pharm. 2022, 611, 121311. [Google Scholar] [CrossRef]
- Karashima, M.; Sano, N.; Yamamoto, S.; Arai, Y.; Yamamoto, K.; Amano, N.; Ikeda, Y. Enhanced pulmonary absorption of poorly soluble itraconazole by micronized cocrystal dry powder formulations. Eur. J. Pharm. Biopharm. 2017, 115, 65–72. [Google Scholar] [CrossRef]
- Alwossabi, A.M.; Elamin, E.S.; Ahmed, E.M.M.; Abdelrahman, M. Solubility enhancement of some poorly soluble drugs by solid dispersion using Ziziphus spina-christi gum polymer. Saudi Pharm. J. 2022, 30, 711–725. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.Y.; Kim, H.; Moon, Y.; Kwak, S.; Kang, C.G.; Park, C.; Jo, J.H.; Kim, S.W.; Pal, K.; Kang, D.H.; et al. Enhancement of the water solubility and antioxidant capacities of mangiferin by transglucosylation using a cyclodextrin glycosyltransferase. Enzyme Microb. Technol. 2022, 159, 110065. [Google Scholar] [CrossRef]
- Volkova, T.V.; Drozd, K.V.; Surov, A.O. Effect of polymers and cyclodextrins on solubility, permeability and distribution of enzalutamide and apalutamide antiandrogens. J. Mol. Liq. 2021, 322, 114937. [Google Scholar] [CrossRef]
- Korn, C.; Balbach, S. Compound selection for development–Is salt formation the ultimate answer? Experiences with an extended concept of the “100 mg approach”. Eur. J. Pharm. Sci. 2014, 57, 257–263. [Google Scholar] [CrossRef] [PubMed]
- Suresh, A.; Gonde, S.; Mondal, P.K.; Sahoo, J.; Chopra, D. Improving solubility and intrinsic dissolution rate of ofloxacin API through salt formation via mechanochemical synthesis with diphenic acid. J. Mol. Struct. 2020, 1221, 128806. [Google Scholar] [CrossRef]
- Liu, L.; Zou, D.; Zhang, Y.; Zhang, Q.; Feng, Y.; Guo, Y.; Liu, Y.; Zhang, X.; Cheng, G.; Wang, C.; et al. Pharmaceutical salts/cocrystals of enoxacin with dicarboxylic acids: Enhancing in vitro antibacterial activity of enoxacin by improving the solubility and permeability. Eur. J. Pharm. Biopharm. 2020, 154, 62–73. [Google Scholar] [CrossRef]
- Nikam, V.J.; Patil, S.B. Pharmaceutical cocrystals of nebivolol hydrochloride with enhanced solubility. J. Cryst. Growth 2020, 534, 125488. [Google Scholar] [CrossRef]
- Blanco-Márquez, J.H.; Caviedes Rubio, D.I.; Ortiz, C.P.; Cerquera, N.E.; Martínez, F.; Delgado, D.R. Thermodynamic analysis and preferential solvation of sulfamethazine in acetonitrile + water cosolvent mixtures. Fluid Phase Equilib. 2020, 505, 112361. [Google Scholar] [CrossRef]
- Smith, P.E.; Mazo, R.M. On the theory of solute solubility in mixed solvents. J. Phys. Chem. B 2008, 112, 7875–7884. [Google Scholar] [CrossRef] [Green Version]
- Jouyban, A. Review of the cosolvency models for predicting solubility of drugs in water-cosolvent mixtures. J. Pharm. Pharm. Sci. 2008, 11, 32–58. [Google Scholar] [CrossRef]
- Lenoir, D.; Schramm, K.W.; Lalah, J.O. Green Chemistry: Some important forerunners and current issues. Sustain. Chem. Pharm. 2020, 18, 100313. [Google Scholar] [CrossRef]
- Constable, D.J.C. Green and sustainable chemistry–The case for a systems-based, interdisciplinary approach. iScience 2021, 24, 103489. [Google Scholar] [CrossRef] [PubMed]
- Hessel, V.; Tran, N.N.; Asrami, M.R.; Tran, Q.D.; Van Duc Long, N.; Escribà-Gelonch, M.; Tejada, J.O.; Linke, S.; Sundmacher, K. Sustainability of green solvents–review and perspective. Green Chem. 2022, 24, 410–437. [Google Scholar] [CrossRef]
- Nanda, B.; Sailaja, M.; Mohapatra, P.; Pradhan, R.K.; Nanda, B.B. Green solvents: A suitable alternative for sustainable chemistry. Mater. Today Proc. 2021, 47, 1234–1240. [Google Scholar] [CrossRef]
- Smith, E.L.; Abbott, A.P.; Ryder, K.S. Deep Eutectic Solvents (DESs) and Their Applications. Chem. Rev. 2014, 114, 11060–11082. [Google Scholar] [CrossRef] [Green Version]
- Omar, K.A.; Sadeghi, R. Physicochemical properties of deep eutectic solvents: A review. J. Mol. Liq. 2022, 360, 119524. [Google Scholar] [CrossRef]
- Zhang, Q.; De Oliveira Vigier, K.; Royer, S.; Jérôme, F. Deep eutectic solvents: Syntheses, properties and applications. Chem. Soc. Rev. 2012, 41, 7108–7146. [Google Scholar] [CrossRef]
- Choi, Y.H.; van Spronsen, J.; Dai, Y.; Verberne, M.; Hollmann, F.; Arends, I.W.C.E.; Witkamp, G.-J.; Verpoorte, R. Are natural deep eutectic solvents the missing link in understanding cellular metabolism and physiology? Plant Physiol. 2011, 156, 1701–1705. [Google Scholar] [CrossRef] [Green Version]
- Dai, Y.; van Spronsen, J.; Witkamp, G.-J.; Verpoorte, R.; Choi, Y.H. Natural deep eutectic solvents as new potential media for green technology. Anal. Chim. Acta 2013, 766, 61–68. [Google Scholar] [CrossRef]
- Jurić, T.; Uka, D.; Holló, B.B.; Jović, B.; Kordić, B.; Popović, B.M. Comprehensive physicochemical evaluation of choline chloride-based natural deep eutectic solvents. J. Mol. Liq. 2021, 343, 116968. [Google Scholar] [CrossRef]
- Espino, M.; de los Ángeles Fernández, M.; Gomez, F.J.V.; Silva, M.F. Natural designer solvents for greening analytical chemistry. TrAC Trends Anal. Chem. 2016, 76, 126–136. [Google Scholar] [CrossRef]
- Xu, G.; Shi, M.; Zhang, P.; Tu, Z.; Hu, X.; Zhang, X.; Wu, Y. Tuning the composition of deep eutectic solvents consisting of tetrabutylammonium chloride and n-decanoic acid for adjustable separation of ethylene and ethane. Sep. Purif. Technol. 2022, 298, 121680. [Google Scholar] [CrossRef]
- Paiva, A.; Craveiro, R.; Aroso, I.; Martins, M.; Reis, R.L.; Duarte, A.R.C. Natural Deep Eutectic Solvents–Solvents for the 21st Century. ACS Sustain. Chem. Eng. 2014, 2, 1063–1071. [Google Scholar] [CrossRef]
- Cao, Y.; Tao, X.; Jiang, S.; Gao, N.; Sun, Z. Tuning thermodynamic properties of deep eutectic solvents for achieving highly efficient photothermal sensor. J. Mol. Liq. 2020, 308, 113163. [Google Scholar] [CrossRef]
- Liu, Y.; Wu, Y.; Liu, J.; Wang, W.; Yang, Q.; Yang, G. Deep eutectic solvents: Recent advances in fabrication approaches and pharmaceutical applications. Int. J. Pharm. 2022, 622, 121811. [Google Scholar] [CrossRef]
- Bakirtzi, C.; Triantafyllidou, K.; Makris, D.P. Novel lactic acid-based natural deep eutectic solvents: Efficiency in the ultrasound-assisted extraction of antioxidant polyphenols from common native Greek medicinal plants. J. Appl. Res. Med. Aromat. Plants 2016, 3, 120–127. [Google Scholar] [CrossRef]
- Moradi, G.; Rahimi, M.; Zinadini, S.; Shamsipur, M.; Babajani, N. Natural deep eutectic solvent modified nanofiltration membranes with superior antifouling properties for pharmaceutical wastewater treatment. Chem. Eng. J. 2022, 448, 137704. [Google Scholar] [CrossRef]
- Durando, M.; Tiu, H.; Kim, J.S. Sulfasalazine-Induced Crystalluria Causing Severe Acute Kidney Injury. Am. J. Kidney Dis. 2017, 70, 869–873. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.; Lee, P.I. Investigation on drug solubility enhancement using deep eutectic solvents and their derivatives. Int. J. Pharm. 2016, 505, 283–288. [Google Scholar] [CrossRef]
- Zhong, J.; Tang, N.; Asadzadeh, B.; Yan, W. Measurement and Correlation of Solubility of Theobromine, Theophylline, and Caffeine in Water and Organic Solvents at Various Temperatures. J. Chem. Eng. Data 2017, 62, 2570–2577. [Google Scholar] [CrossRef]
- Shalmashi, A.; Golmohammad, F. Solubility of caffeine in water, ethyl acetate, ethanol, carbon tetrachloride, methanol, chloroform, dichloromethane, and acetone between 298 and 323 K. Lat. Am. Appl. Res. 2010, 40, 283–285. [Google Scholar]
- Dabir, T.O.; Gaikar, V.G.; Jayaraman, S.; Mukherjee, S. Thermodynamic modeling studies of aqueous solubility of caffeine, gallic acid and their cocrystal in the temperature range of 303 K–363 K. Fluid Phase Equilib. 2018, 456, 65–76. [Google Scholar] [CrossRef]
- Rezaei, H.; Rahimpour, E.; Ghafourian, T.; Martinez, F.; Barzegar-Jalali, M.; Jouyban, A. Solubility of caffeine in N-methyl-2-pyrrolidone + ethanol mixture at different temperatures. J. Mol. Liq. 2020, 300, 112354. [Google Scholar] [CrossRef]
- Rezaei, H.; Rahimpour, E.; Martinez, F.; Zhao, H.; Jouyban, A. Study and mathematical modeling of caffeine solubility in N-methyl-2-pyrrolidone + ethylene glycol mixture at different temperatures. J. Mol. Liq. 2021, 341, 117350. [Google Scholar] [CrossRef]
- Golubev, V.A.; Gurina, D.L. Dissolving power of the binary solvent carbon tetrachloride–methanol. Solubility of caffeine: Experiment, ASL model, and MD simulation. J. Mol. Liq. 2021, 344, 117736. [Google Scholar] [CrossRef]
- Bustamante, P.; Navarro, J.; Romero, S.; Escalera, B. Thermodynamic Origin of the Solubility Profile of Drugs Showing one or two Maxima Against the Polarity of Aqueous and Nonaqueous Mixtures: Niflumic Acid and Caffeine. J. Pharm. Sci. 2002, 91, 874–883. [Google Scholar] [CrossRef]
- Cárdenas, Z.J.; Jiménez, D.M.; Almanza, O.A.; Jouyban, A.; Martínez, F.; Acree, W.E. Solubility and Preferential Solvation of Caffeine and Theophylline in {Methanol + Water} Mixtures at 298.15 K. J. Solut. Chem. 2017, 46, 1605–1624. [Google Scholar] [CrossRef]
- Adjei, A.; Newburger, J.; Martin, A. Extended hildebrand approach: Solubility of caffeine in dioxane–water mixtures. J. Pharm. Sci. 1980, 69, 659–661. [Google Scholar] [CrossRef]
- Rezaei, H.; Rahimpour, E.; Martinez, F.; Jouyban, A. Solubility of caffeine in carbitol + ethanol mixture at different temperatures. J. Mol. Liq. 2020, 301, 112465. [Google Scholar] [CrossRef]
- Rezaei, H.; Jouyban, A.; Zhao, H.; Martinez, F.; Rahimpour, E. Solubility of caffeine in N-methyl-2-pyrrolidone + 1-propanol mixtures at different temperatures. J. Mol. Liq. 2021, 117067. [Google Scholar] [CrossRef]
- Rezaei, H.; Rahimpour, E.; Zhao, H.; Martinez, F.; Jouyban, A. Solubility measurement and thermodynamic modeling of caffeine in N-methyl-2-pyrrolidone + isopropanol mixtures at different temperatures. J. Mol. Liq. 2021, 336, 116519. [Google Scholar] [CrossRef]
- Rezaei, H.; Rahimpour, E.; Zhao, H.; Martinez, F.; Jouyban, A. Determination and modeling of caffeine solubility in N-methyl-2-pyrrolidone + propylene glycol mixtures. J. Mol. Liq. 2021, 343, 117613. [Google Scholar] [CrossRef]
- Lentz, H.; Gehrig, M.; Schulmeyer, J. Dynamic solubility measurements of caffeine in carbon dioxide and in carbon dioxide saturated with water. Physica B+C 1986, 139–140, 70–72. [Google Scholar] [CrossRef]
- Johannsen, M.; Brunner, G. Solubilities of the xanthines caffeine, theophylline and theobromine in supercritical carbon dioxide. Fluid Phase Equilib. 1994, 95, 215–226. [Google Scholar] [CrossRef]
- Jeliński, T.; Kubsik, M.; Cysewski, P. Application of the Solute-Solvent Intermolecular Interactions as Indicator of Caffeine Solubility in Aqueous Binary Aprotic and Proton Acceptor Solvents: Measurements and Quantum Chemistry Computations. Materials 2022, 15, 2472. [Google Scholar] [CrossRef]
- Ferreira, A.M.; Gomes, H.M.D.; Coutinho, J.A.P.; Freire, M.G. Valorization of Spent Coffee by Caffeine Extraction Using Aqueous Solutions of Cholinium-Based Ionic Liquids. Sustainability 2021, 13, 7509. [Google Scholar] [CrossRef]
- Cláudio, A.F.M.; Ferreira, A.M.; Freire, M.G.; Coutinho, J.A.P. Enhanced extraction of caffeine from guaraná seeds using aqueous solutions of ionic liquids. Green Chem. 2013, 15, 2002–2010. [Google Scholar] [CrossRef]
- Basaiahgari, A.; Priyanka, V.P.; Ijardar, S.P.; Gardas, R.L. Aqueous biphasic systems of amino acid-based ionic liquids: Evaluation of phase behavior and extraction capability for caffeine. Fluid Phase Equilib. 2020, 506, 112373. [Google Scholar] [CrossRef]
- Yazdabadi, A.; Shahriari, S.; Salehifar, M. Extraction of caffeine using aqueous two-phase systems containing ionic liquid and sorbitol. Fluid Phase Equilib. 2019, 502, 112287. [Google Scholar] [CrossRef]
- Cai, C.; Li, F.; Liu, L.; Tan, Z. Deep eutectic solvents used as the green media for the efficient extraction of caffeine from Chinese dark tea. Sep. Purif. Technol. 2019, 227, 115723. [Google Scholar] [CrossRef]
- Waters, K.L.; Beal, G.D. Notes on the water content of crystalline caffeine. J. Am. Pharm. Assoc. Am. Pharm. Assoc. 1946, 35, 12–14. [Google Scholar] [CrossRef] [PubMed]
- Bogardus, J.B. Crystalline anhydrous-hydrate phase changes of caffeine and theophylline in solvent-water mixtures. J. Pharm. Sci. 1983, 72, 837–838. [Google Scholar] [CrossRef] [PubMed]
- Pirttimäki, J.; Laine, E. The transformation of anhydrate and hydrate forms of caffeine at 100% RH and 0% RH. Eur. J. Pharm. Sci. 1994, 1, 203–208. [Google Scholar] [CrossRef]
- Edwards, H.G.M.; Lawson, E.; Matas, M.D.; Shields, L.; York, P. Metamorphosis of caffeine hydrate and anhydrous caffeine. J. Chem. Soc. Perkin Trans. 2 1997, 1985–1990. [Google Scholar] [CrossRef]
- Dong, J.X.; Li, Q.; Tan, Z.C.; Zhang, Z.H.; Liu, Y. The standard molar enthalpy of formation, molar heat capacities, and thermal stability of anhydrous caffeine. J. Chem. Thermodyn. 2007, 1, 108–114. [Google Scholar] [CrossRef]
- Dichi, E.; Legendre, B.; Sghaier, M. Physico-chemical characterisation of a new polymorph of caffeine. J. Therm. Anal. Calorim. 2014, 115, 1551–1561. [Google Scholar] [CrossRef]
- González-González, J.S.; Zúñiga-Lemus, O.; Hernández-Galindo, M.D. Hydrated Solid Forms of Theophylline and Caffeine Obtained by Mechanochemistry. IOSR J. Pharm. 2017, 7, 28–30. [Google Scholar]
- Cysewski, P.; Jeliński, T.; Cymerman, P.; Przybyłek, M. Solvent Screening for Solubility Enhancement of Theophylline in Neat, Binary and Ternary NADES Solvents: New Measurements and Ensemble Machine Learning. Int. J. Mol. Sci. 2021, 22, 7347. [Google Scholar] [CrossRef]
- Jeliński, T.; Stasiak, D.; Kosmalski, T.; Cysewski, P. Experimental and Theoretical Study on Theobromine Solubility Enhancement in Binary Aqueous Solutions and Ternary Designed Solvents. Pharmaceutics 2021, 13, 1118. [Google Scholar] [CrossRef]
- Jeliński, T.; Przybyłek, M.; Cysewski, P. Natural Deep Eutectic Solvents as Agents for Improving Solubility, Stability and Delivery of Curcumin. Pharm. Res. 2019, 36, 116. [Google Scholar] [CrossRef] [Green Version]
- Jeliński, T.; Przybyłek, M.; Cysewski, P. Solubility advantage of sulfanilamide and sulfacetamide in natural deep eutectic systems: Experimental and theoretical investigations. Drug Dev. Ind. Pharm. 2019, 45, 1120–1129. [Google Scholar] [CrossRef] [PubMed]
- Verheijen, M.; Lienhard, M.; Schrooders, Y.; Clayton, O.; Nudischer, R.; Boerno, S.; Timmermann, B.; Selevsek, N.; Schlapbach, R.; Gmuender, H.; et al. DMSO induces drastic changes in human cellular processes and epigenetic landscape in vitro. Sci. Rep. 2019, 9, 4641. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kim, T.H.; Kim, S.G. Clinical Outcomes of Occupational Exposure to N,N-Dimethylformamide: Perspectives from Experimental Toxicology. Saf. Health Work 2011, 2, 97–104. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sachsenhauser, T.; Rehfeldt, S.; Klamt, A.; Eckert, F.; Klein, H. Consideration of dimerization for property prediction with COSMO-RS-DARE. Fluid Phase Equilib. 2014, 382, 89–99. [Google Scholar] [CrossRef]
- Klamt, A.; Eckert, F.; Arlt, W. COSMO-RS: An Alternative to Simulation for Calculating Thermodynamic Properties of Liquid Mixtures. Annu. Rev. Chem. Biol. Eng. 2010, 1, 101–122. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Klamt, A. COSMO-RS: From Quantum Chemistry to Fluid Phase Thermodynamics and Drug Design, 1st ed.; Elsevier Science: Amsterdam, The Netherlands, 2005. [Google Scholar]
- Klamt, A.; Smith, B.J. Challenge of Drug Solubility Prediction. In Molecular Drug Properties: Measurement and Prediction; Methods and Principles in Medicinal Chemistry, 1st ed.; Mannhold, R., Kubinyi, H., Folkers, G., Eds.; Wiley-VCH: Weinheim, Germany, 2008; pp. 283–311. [Google Scholar]
- Przybyłek, M.; Miernicka, A.; Nowak, M.; Cysewski, P. New Screening Protocol for Effective Green Solvents Selection of Benzamide, Salicylamide and Ethenzamide. Molecules 2022, 27, 3323. [Google Scholar] [CrossRef] [PubMed]
- Cysewski, P. Prediction of ethenzamide solubility in organic solvents by explicit inclusions of intermolecular interactions within the framework of COSMO-RS-DARE. J. Mol. Liq. 2019, 290, 111163. [Google Scholar] [CrossRef]
- Cysewski, P.; Przybyłek, M.; Kowalska, A.; Tymorek, N. Thermodynamics and Intermolecular Interactions of Nicotinamide in Neat and Binary Solutions: Experimental Measurements and COSMO-RS Concentration Dependent Reactions Investigations. Int. J. Mol. Sci. 2021, 22, 7365. [Google Scholar] [CrossRef]
- Cysewski, P.; Przybyłek, M.; Rozalski, R. Experimental and theoretical screening for green solvents improving sulfamethizole solubility. Materials 2021, 14, 5915. [Google Scholar] [CrossRef]
- Prausintz, J.M.; Lichtenthaler, R.N.; de Azevedo, E.G. Molecular Thermodynamics of Fluid-Phase Equilibria, 3rd ed.; Prentice Hall: Englewood Cliffs, NJ, USA, 1999. [Google Scholar]
- Svärd, M.; Valavi, M.; Khamar, D.; Kuhs, M.; Rasmuson, Å.C. Thermodynamic Stability Analysis of Tolbutamide Polymorphs and Solubility in Organic Solvents. J. Pharm. Sci. 2016, 105, 1901–1906. [Google Scholar] [CrossRef] [Green Version]
- Nordström, F.L.; Rasmuson, Å.C. Determination of the activity of a molecular solute in saturated solution. J. Chem. Thermodyn. 2008, 40, 1684–1692. [Google Scholar] [CrossRef]
- Abraham, M.H.; Acree, W.E. Estimation of enthalpies of sublimation of organic, organometallic and inorganic compounds. Fluid Phase Equilib. 2020, 515, 112575. [Google Scholar] [CrossRef]
- Jasim, F.; Talib, T. Some observations on the thermal behaviour of curcumin under air and argon atmospheres. J. Therm. Anal. 1992, 38, 2549–2552. [Google Scholar] [CrossRef]
- Kulkarni, P.P.; Jafvert, C.T. Solubility of C60 in solvent mixtures. Environ. Sci. Technol. 2008, 42, 845–851. [Google Scholar] [CrossRef]
- Manin, A.N.; Drozd, K.V.; Voronin, A.P.; Churakov, A.V.; Perlovich, G.L. A Combined Experimental and Theoretical Study of Nitrofuran Antibiotics: Crystal Structures, DFT Computations, Sublimation and Solution Thermodynamics. Molecules 2021, 26, 3444. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, Y.; Shi, P.; Du, S.; Liu, Y.; Han, D.; Sun, P.; Sun, M.; Xu, S.; Gong, J. Uncover the effect of solvent and temperature on solid-liquid equilibrium behavior of l-norvaline. J. Mol. Liq. 2017, 243, 273–284. [Google Scholar] [CrossRef]
- Sun, P.; Liu, Y.; Du, S.; Yu, B.; Wang, Y.; Sun, M.; Shi, P.; Liu, Y.; Gong, J. Temperature-dependent solubility of β-Alanine in different binary solvents from 288.15 K to 323.15 K: Measurement and thermodynamic modeling. J. Mol. Liq. 2017, 232, 522–531. [Google Scholar] [CrossRef]
- Marrero, J.; Gani, R. Group-contribution based estimation of pure component properties. Fluid Phase Equilib. 2001, 183–184, 183–208. [Google Scholar] [CrossRef]
- Jain, A.; Yang, G.; Yalkowsky, S.H. Estimation of melting points of organic compounds. Ind. Eng. Chem. Res. 2004, 43, 7618–7621. [Google Scholar] [CrossRef] [Green Version]
- Acree, W.; Chickos, J.S. Phase Transition Enthalpy Measurements of Organic and Organometallic Compounds. Sublimation, Vaporization and Fusion Enthalpies From 1880 to 2010. J. Phys. Chem. Ref. Data 2010, 39, 43101. [Google Scholar] [CrossRef]
- Boumrah, Y.; Bouanani, S.; Khimeche, K.; Dahmani, A. Analysis of synthetic drugs by differential scanning calorimetry: Case of amphetamine-type stimulants (ATS). J. Therm. Anal. Calorim. 2015, 120, 583–590. [Google Scholar] [CrossRef]
- Klímová, K.; Leitner, J. DSC study and phase diagrams calculation of binary systems of paracetamol. Thermochim. Acta 2012, 550, 59–64. [Google Scholar] [CrossRef]
- Agafonova, E.V.; Moshchenskii, Y.V.; Tkachenko, M.L. Determining the main thermodynamic parameters of caffeine melting by means of DSC. Russ. J. Phys. Chem. A 2012, 86, 1035–1037. [Google Scholar] [CrossRef]
- Manic, M.S.; Villanueva, D.; Fornari, T.; Queimada, A.J.; MacEdo, E.A.; Najdanovic-Visak, V. Solubility of high-value compounds in ethyl lactate: Measurements and modeling. J. Chem. Thermodyn. 2012, 48, 93–100. [Google Scholar] [CrossRef] [Green Version]
- Baird, J.A.; Van Eerdenbrugh, B.; Taylor, L.S. A classification system to assess the crystallization tendency of organic molecules from undercooled melts. J. Pharm. Sci. 2010, 99, 3787–3806. [Google Scholar] [CrossRef] [PubMed]
- Guo, K.; Sadiq, G.; Seaton, C.; Davey, R.; Yin, Q. Co-crystallization in the caffeine/maleic acid system: Lessons from phase equilibria. Cryst. Growth Des. 2010, 10, 268–273. [Google Scholar] [CrossRef]
- Mogalian, E.; Sepassi, K.; Myrdal, P.B. Accounting for the effects of moderately increased pressure on the energetics of melting and solubility in metered dose inhalers. Drug Dev. Ind. Pharm. 2008, 34, 930–935. [Google Scholar] [CrossRef]
- Wesolowski, M.; Szynkaruk, P. Thermal decomposition of methylxanthines. J. Therm. Anal. Calorim. 2008, 93, 739–746. [Google Scholar] [CrossRef]
- Saganowska, P.; Wesolowski, M. DSC as a screening tool for rapid co-crystal detection in binary mixtures of benzodiazepines with co-formers. J. Therm. Anal. Calorim. 2018, 133, 785–795. [Google Scholar] [CrossRef] [Green Version]
- Dassault Systèmes. COSMOtherm, Version 22.0.0, Dassault Systèmes, Biovia: San Diego, CA, USA, 2022.
- Dassault Systèmes. Reference Manual, BIOVIA COSMOtherm, Version 22.0.0; Dassault Systèmes, Biovia: San Diego, CA, USA, 2022; pp. 263–266. [Google Scholar]
- Hellweg, A.; Eckert, F. Brick by brick computation of the gibbs free energy of reaction in solution using quantum chemistry and COSMO-RS. AIChE J. 2017, 63, 3944–3954. [Google Scholar] [CrossRef]
- Witte, J.; Neaton, J.B.; Head-Gordon, M. Effective empirical corrections for basis set superposition error in the def2-SVPD basis: gCP and DFT-C. J. Chem. Phys. 2017, 146, 234105. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Klamt, A. Conductor-like screening model for real solvents: A new approach to the quantitative calculation of solvation phenomena. J. Phys. Chem. 1995, 99, 2224–2235. [Google Scholar] [CrossRef]
- Klamt, A.; Jonas, V.; Bürger, T.; Lohrenz, J.C.W. Refinement and parametrization of COSMO-RS. J. Phys. Chem. A 1998, 102, 5074–5085. [Google Scholar] [CrossRef]
- Eckert, F.; Klamt, A. Fast solvent screening via quantum chemistry: COSMO-RS approach. AIChE J. 2002, 48, 369–385. [Google Scholar] [CrossRef] [Green Version]
- Dassault Systèmes. COSMOconf, Version 20.0.0, Dassault Systèmes, Biovia: San Diego, CA, USA, 2020.
- Dassault Systèmes. TmoleX, Version 21.0.1, Dassault Systèmes, Biovia: San Diego, CA, USA, 2020.
- TURBOMOLE GmbH. TURBOMOLE, Version 7.5.1, TURBOMOLE GmbH: Frankfurt, Germany, 2020.













| Type of Interaction | ΔGr(a)COSMO-RS | ΔGr(a)final | |||||
|---|---|---|---|---|---|---|---|
| C + C | 20.20 | 0.22 | 25.57 | 0.18 | 31.66 | 0.12 | 38.27 |
| C + ChCl | 24.49 | 0.32 | 28.60 | 0.15 | 35.03 | 0.30 | 41.54 |
| C + GL | 28.41 | 0.46 | 33.52 | 0.28 | 39.94 | 0.33 | 47.57 |
| C + SO | 33.43 | 0.22 | 38.71 | 0.53 | 45.28 | 0.49 | 53.98 |
| C + XY | 39.27 | 0.25 | 46.85 | 0.60 | 54.10 | 0.63 | 64.45 |
| C + GU | 48.61 | 0.27 | 56.66 | 0.43 | 65.80 | 0.67 | 76.38 |
| C + W | 60.99 | 0.36 | 69.65 | 0.59 | 79.81 | 0.99 | 95.54 |
| System | α; β | γ; δ |
|---|---|---|
| [ChCl + glycerol + water] | 21.93; −10.63 | 9.00; −5.68 |
| [ChCl + sorbitol + water] | 22.39; −10.99 | 8.84; −6.11 |
| [ChCl + xylitol + water] | 18.90; −9.93 | 4.35; −4.73 |
| [ChCl + glucose + water] | 27.73; −7.37 | 13.61; −12.62 |
| [ChCl + glycerol + water] | 21.93; −10.63 | 9.00; −5.68 |
| Tm [K] | Hfus [kJ/mol] |
|---|---|
| 509.05 1 510.2 [116], 510.3 [88], 508.8 [117], 508.7 [118], 505.4 [119], 510.0 [120], 507.7 [121], 509.6 [122], 509.1 [62], 510.8 [123] | 20.66 1 20.08 [116], 19.52 [88], 20.37 [117], 19.60 [118], 17.90 [119], 20.80 [120], 24.80 [121], 23.46 [122], 20.29 [124], 19.44 [62], 20.95 [123] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jeliński, T.; Cysewski, P. Quantification of Caffeine Interactions in Choline Chloride Natural Deep Eutectic Solvents: Solubility Measurements and COSMO-RS-DARE Interpretation. Int. J. Mol. Sci. 2022, 23, 7832. https://doi.org/10.3390/ijms23147832
Jeliński T, Cysewski P. Quantification of Caffeine Interactions in Choline Chloride Natural Deep Eutectic Solvents: Solubility Measurements and COSMO-RS-DARE Interpretation. International Journal of Molecular Sciences. 2022; 23(14):7832. https://doi.org/10.3390/ijms23147832
Chicago/Turabian StyleJeliński, Tomasz, and Piotr Cysewski. 2022. "Quantification of Caffeine Interactions in Choline Chloride Natural Deep Eutectic Solvents: Solubility Measurements and COSMO-RS-DARE Interpretation" International Journal of Molecular Sciences 23, no. 14: 7832. https://doi.org/10.3390/ijms23147832
APA StyleJeliński, T., & Cysewski, P. (2022). Quantification of Caffeine Interactions in Choline Chloride Natural Deep Eutectic Solvents: Solubility Measurements and COSMO-RS-DARE Interpretation. International Journal of Molecular Sciences, 23(14), 7832. https://doi.org/10.3390/ijms23147832