Tunable Microcavity-Stabilized Quantum Cascade Laser for Mid-IR High-Resolution Spectroscopy and Sensing
Abstract
:1. Introduction
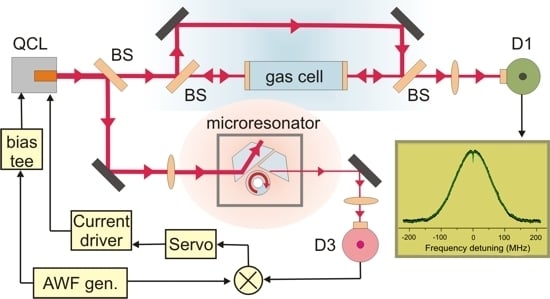
2. Experimental Section
3. Noise Analysis
4. Spectroscopic Results
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Galli, I.; Bartalini, S.; Borri, S.; Cancio Pastor, P.; Mazzotti, D.; De Natale, P.; Giusfredi, G. Molecular Gas Sensing below Parts per Trillion: Radiocarbon-Dioxide Optical Detection. Phys. Rev. Lett. 2011, 107. [Google Scholar] [CrossRef] [PubMed]
- Mazzotti, D.; Cancio Pastor, P.; Giusfredi, G.; Inguscio, M.; De Natale, P. Search for Exchange-Antisymmetric States for Spin-0 Particles at the 10−11 Level. Phys. Rev. Lett. 2001, 86, 1919–1922. [Google Scholar] [CrossRef] [PubMed]
- Tokunaga, S.K.; Stoeffler, C.; Auguste, F.; Shelkovnikov, A.; Daussy, C.; Amy-Klein, A.; Chardonnet, C.; Darquié, B. Probing weak force-induced parity violation by high-resolution mid-infrared molecular spectroscopy. Mol. Phys. 2013, 111, 2363–2373. [Google Scholar] [CrossRef]
- Shelkovnikov, A.; Butcher, R.J.; Chardonnet, C.; Amy-Klein, A. Stability of the proton-to-electron mass ratio. Phys. Rev. Lett. 2008, 100. [Google Scholar] [CrossRef] [PubMed]
- Jansen, P.; Bethlem, H.L.; Ubachs, W. Perspective: Tipping the scales: Search for drifting constants from molecular spectra. J. Chem. Phys. 2014, 140. [Google Scholar] [CrossRef] [PubMed]
- Cancio Pastor, P.; Galli, I.; Giusfredi, G.; Mazzotti, D.; De Natale, P. Testing the validity of Bose-Einstein statistics in molecules. Phys. Rev. A 2015, 92. [Google Scholar] [CrossRef]
- Bartalini, S.; Borri, S.; Cancio Pastor, P.; Castrillo, A.; Galli, I.; Giusfredi, G.; Mazzotti, D.; Gianfrani, L.; De Natale, P. Observing the Intrinsic Linewidth of a Quantum-Cascade Laser: Beyond the Schawlow-Townes Limit. Phys. Rev. Lett. 2010, 104. [Google Scholar] [CrossRef] [PubMed]
- Cappelli, F.; Villares, G.; Riedi, S.; Faist, J. Intrinsic linewidth of quantum cascade laser frequency combs. Optica 2015, 2, 836–840. [Google Scholar] [CrossRef]
- Borri, S.; Bartalini, S.; Cancio Pastor, P.; Galli, I.; Giusfredi, G.; Mazzotti, D.; De Natale, P. Quantum cascade lasers for high-resolution spectroscopy. Opt. Eng. 2010, 49. [Google Scholar] [CrossRef]
- Borri, S.; Bartalini, S.; Galli, I.; Cancio Pastor, P.; Giusfredi, G.; Mazzotti, D.; Castrillo, A.; Gianfrani, L.; De Natale, P. Lamb-dip-locked quantum cascade laser for comb-referenced IR absolute frequency measurements. Opt. Express 2008, 16, 11637–11646. [Google Scholar] [CrossRef] [PubMed]
- Galli, I.; Siciliani de Cumis, M.; Cappelli, F.; Bartalini, S.; Mazzotti, D.; Borri, S.; Montori, A.; Akikusa, N.; Yamanishi, M.; Giusfredi, G.; et al. Comb-assisted subkilohertz linewidth quantum cascade laser for high-precision mid-infrared spectroscopy. Appl. Phys. Lett. 2013, 102. [Google Scholar] [CrossRef]
- Argence, B.; Chanteau, B.; Lopez, O.; Nicolodi, D.; Abgrall, M.; Chardonnet, C.; Daussy, C.; Darquié, B.; Le Coq, Y.; Amy-Klein, A. Quantum cascade laser frequency stabilization at the sub-Hz level. Nat. Photon. 2015, 9, 456–461. [Google Scholar] [CrossRef] [Green Version]
- Hansen, M.G.; Magoulakis, E.; Chen, Q.-F.; Ernsting, I.; Schiller, S. Quantum cascade laser-based mid-IR frequency metrology system with ultra-narrow linewidth and 1×10−13-level frequency instability. Opt. Lett. 2015, 40, 2289–2292. [Google Scholar] [CrossRef] [PubMed]
- Cappelli, F.; Galli, I.; Borri, S.; Giusfredi, G.; Cancio Pastor, P.; Mazzotti, D.; Montori, A.; Akikusa, N.; Yamanishi, M.; Bartalini, S.; et al. Subkilohertz linewidth room-temperature mid-infrared quantum cascade laser using a molecular sub-Doppler reference. Opt. Lett. 2012, 37, 4811–4813. [Google Scholar] [CrossRef] [PubMed]
- Siciliani de Cumis, M.; Borri, S.; Insero, G.; Galli, I.; Savchenkov, A.; Eliyahu, D.; Ilchenko, V.; Akikusa, N.; Matsko, A.; Maleki, L.; et al. Microcavity-Stabilized Quantum Cascade Laser. Laser Photon. Rev. 2016, 10, 153–157. [Google Scholar] [CrossRef]
- Matsko, A.B.; Ilchenko, V.S. Optical Resonators with Whispering-Gallery Modes—Part I: Basics. IEEE J. Sel. Top. Quantum Electron. 2006, 12, 3–14. [Google Scholar] [CrossRef]
- Ilchenko, V.S.; Matsko, A.B. Optical Resonators with Whispering-Gallery Modes—Part II: Applications. IEEE J. Sel. Top. Quantum Electron. 2006, 12, 15–32. [Google Scholar] [CrossRef]
- Kippenberg, T.J.; Holzwarth, R.; Diddams, S.A. Microresonator-Based Optical Frequency Combs. Science 2011, 332, 555–559. [Google Scholar] [CrossRef] [PubMed]
- Savchenkov, A.A.; Ilchenko, V.S.; Di Teodoro, F.; Belden, P.M.; Lotshaw, W.T.; Matsko, A.B.; Maleki, L. Generation of Kerr combs centered at 4.5 μm in crystalline microresonators pumped with quantum-cascade lasers. Opt. Lett. 2015, 40, 3468–3471. [Google Scholar] [CrossRef] [PubMed]
- Savchenkov, A.A.; Matsko, A.B.; Ilchenko, V.S.; Yu, N.; Maleki, L. Whispering-gallery-mode resonators as frequency references. II. Stabilization. J. Opt. Soc. Am. B 2007, 24, 2988–2997. [Google Scholar] [CrossRef]
- Liang, W.; Ilchenko, V.S.; Eliyahu, D.; Savchenkov, A.A.; Matsko, A.B.; Seidel, B.; Maleki, L. Ultralow noise miniature external cavity semiconductor laser. Nat. Commun. 2015, 6. [Google Scholar] [CrossRef] [PubMed]
- Elliott, D.S.; Roy, R.; Smith, S.J. Extracavity laser band-shape and bandwidth modification. Phys. Rev. A 1982, 26, 12–18. [Google Scholar] [CrossRef]







© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Borri, S.; Siciliani de Cumis, M.; Insero, G.; Bartalini, S.; Cancio Pastor, P.; Mazzotti, D.; Galli, I.; Giusfredi, G.; Santambrogio, G.; Savchenkov, A.; et al. Tunable Microcavity-Stabilized Quantum Cascade Laser for Mid-IR High-Resolution Spectroscopy and Sensing. Sensors 2016, 16, 238. https://doi.org/10.3390/s16020238
Borri S, Siciliani de Cumis M, Insero G, Bartalini S, Cancio Pastor P, Mazzotti D, Galli I, Giusfredi G, Santambrogio G, Savchenkov A, et al. Tunable Microcavity-Stabilized Quantum Cascade Laser for Mid-IR High-Resolution Spectroscopy and Sensing. Sensors. 2016; 16(2):238. https://doi.org/10.3390/s16020238
Chicago/Turabian StyleBorri, Simone, Mario Siciliani de Cumis, Giacomo Insero, Saverio Bartalini, Pablo Cancio Pastor, Davide Mazzotti, Iacopo Galli, Giovanni Giusfredi, Gabriele Santambrogio, Anatoliy Savchenkov, and et al. 2016. "Tunable Microcavity-Stabilized Quantum Cascade Laser for Mid-IR High-Resolution Spectroscopy and Sensing" Sensors 16, no. 2: 238. https://doi.org/10.3390/s16020238
APA StyleBorri, S., Siciliani de Cumis, M., Insero, G., Bartalini, S., Cancio Pastor, P., Mazzotti, D., Galli, I., Giusfredi, G., Santambrogio, G., Savchenkov, A., Eliyahu, D., Ilchenko, V., Akikusa, N., Matsko, A., Maleki, L., & De Natale, P. (2016). Tunable Microcavity-Stabilized Quantum Cascade Laser for Mid-IR High-Resolution Spectroscopy and Sensing. Sensors, 16(2), 238. https://doi.org/10.3390/s16020238