1. Introduction
Direction-of-arrival (DOA) refers to the process of retrieving the direction information of several electromagnetic waves from the outputs of a number of receiving antennas that form a sensor array. DOA estimation is a major topic in array signal processing and plays a very important role in many applications, e.g., wireless communications, medical imaging, and radar systems [
1,
2,
3],. Moreover, wireless sensor networks (WSNs) are an emerging paradigm in wireless communications [
4]. In WSNs one of the most significant challenges is localization in which DOA is a major parameter to estimate [
5,
6]. The research on DOA estimation is mainly divided into two aspects: (1) array geometry, such as the recently proposed nested array [
7] and coprime array [
8,
9]. (2) DOA estimation algorithm with higher estimation accuracy. In general, the algorithm applied to DOA estimation may be classified into three parts: nonparametric, parametric, and semiparametric [
10].
A main example of the nonparametric methods is delay-and-sum (DAS) beamformer [
10] in which the received signal from each sensor are weighted and delayed so as to focus on different points in space. It is a data-independent estimation technique which is traditionally adopted due to its low computational burden and high-signal-to-noise ratio (SNR) properties. However, data-independent approaches suffer from leakage problem. The local leakage will reduce the resolution, which makes the DAS beamformer unable to distinguish the incident signals with close frequency components. Global leakage will lead to false alarms. Adaptive Capon beamformer can improve the DAS method, but it is limited to independent signal [
11]. Parametric methods, especially subspace methods such as multiple signal classification (MUSIC) [
12], estimation of signal parameters via rotational invariance techniques (ESPRIT) [
13], where parameters are estimated by studying the subspace of the data covariance. They can provide higher resolution than nonparametric methods, but adimit two shortcomings: (1) they require the knowledge of the number of source, and (2) work well only when the sources are independent. Recently, these two kinds of approaches have been combined, leading to the so-called semiparametric approache. The recently developed iterative adaptive algorithm (IAA) [
14] largely eliminates the leakage problem of the beamformer and is robust to coherent sources. However, the IAA algorithm still has resolution limitations, especially at low SNR situations. Stoica et al. have recently proposed a user parameter-free sparse iterative covariance-based estimation (SPICE) approach in [
15,
16], based on minimizing a covariance fitting criterion. SPICE is able to provide excellent resolution and low sidelobe levels while maintaining robustness to coherent sources. Moreover, the power of the signal can be estimated simultaneously. However, as with most power-based sparse methods, the estimation accuracy of the SPICE algorithm is limited to the direction grid. In addition, the signal power estimated by SPICE is inaccurate, especially in the case of coherent signal. In [
17], a method named likelihood-based estimation of sparse parameters (LIKES) is proposed, where the same covariance fitting criterion is adopted as SPICE algorithm. The difference is that the weights in LIKES are adaptive rather than constant in SPICE. Compared with the SPICE algorithm, LIKES can obtain more accurate DOA estimation, but at the expense of computational cost. The DOA estimation accuracy will be limited to direction grid because the spatial domain is also discretized in LIKES algorithm. In [
18], an iterative algorithm based on the combination of Capon and SPICE (C-SPICE) is proposed, and a mobile average initialization technology is introduced to realize DOA estimation by using the spatial spectrum information estimated in the previous snapshot in the next snapshot.
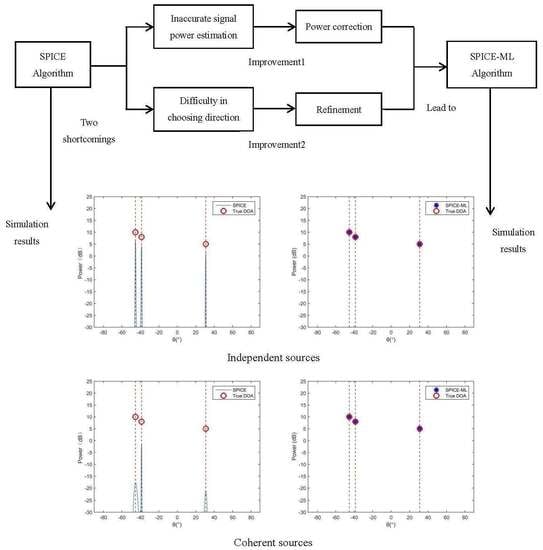
DAS has low computational burden and accurate signal power estimation, but low resolution. The resolution of IAA is improved, but still not high enough to distinguish two signals which are close to each other. SPICE has high resolution, but the signal power estimated by SPICE is not accurate, and the DOA estimation accuracy is limited to the direction grid. In order to obtain an algorithm with high resolution, accurate signal power estimation and high estimation accuracy, we propose a SPICE and maximum likelihood (ML) estimation approach (SPICE-ML) in this paper. An iterative correction process is derived through the asymptotically minimum variance (AMV) criterion [
19,
20] so that the power of the signal estimated are more accurate. Moreover, a maximum likelihood cost function is used to refine the DOA estimation, thereby combating the limit of estimation accuracy caused by the direction grid. Numerical simulations are designed to show the effectiveness and superiority in estimation accuracy of the proposed algorithm.
This paper is organized as follows. The signal model for DOA estimation is introduced in
Section 2 for far-field, narrowband sources. The concept of sparse representation is also discussed in
Section 2. The SPICE algorithm is introduced in
Section 3, including the covariance fitting criterion and updating formulas.
Section 4 is the main highlight of this paper in which the SPICE-ML is proposed. Compared with SPICE algorithm, SPICE-ML can receive more accurate signal power estimation and DOA estimation accuracy. Numerical simulations are presented in
Section 5, and the conclusion and some future research directions are drawn in
Section 6.
Notations: Vectors, matrices are denoted by boldface lowercase letters and boldface uppercase letters, respectively. , , and represent the transpose, the conjugate, the inverse and the complex conjugate transpose of vectors or matrices. ⊗ is the Kronecker product and represents the trace of a matrix. , and denote the operator of expectation, determinant and vectorization. denotes the Euclidean norm for vectors and the Frobenius norm for matrices.
2. Signal Model
Assume
N far-field, uncorrelated narrowband signals from directions
impinging on an uniform line array (ULA), the number of ULA is
M and the inter-element spacing equals to a half of the signal wavelength. Let
denote a direction grid that covers
, where
,
. Assume the direction gird is fine enough so that the true location parameters of the sources lie on (or, practically, close to) the grid. The signal model is shown in
Figure 1.
Then the output of the array can be modeled as:
where
denotes the array manifold matrix and
is the steering vector corresponding to
.
T denotes the number of snapshots.
contains the
K unknown complex-valued signals, and
is the additional noise term. We assume that
, where
is the power of noise, and
is a
identical matrix. Let us further assume that
,
, where
represents the unknown signal power at
. Moreover the signal
and noise
are assumed to be statistically independent. Therefore, we have the covariance matrix of
In practice, this covariance matrix is usually estimated by the sample covariance matrix
Note that only few sources exist in practice, therefore in the signal matrix
only a small number of rows are different from zeros. Thus, the DOA estimation problem is then changed to decide from
which rows of the signal matrix
are non-zero.
3. The SPICE Algorithm
The SPICE algorithm is derived from a robust covariance fitting criterion. It has a sound statistical foundation, it does not require any hyper-parameters, and yet it has global convergence properties. Moreover, the signal and noise power are estimated in a natural manner. Although the signal are assumed to be independent, the SPICE algorithm is still robust to coherent signal [
15]. In this paper, we only consider the case in which
and the variances of noise are identical (see [
15] for the case of
and noise with different variances).
Equation (
2) can be rewrite as
where
The SPICE algorithm considers the following weighted covariance fitting criterion:
a simple calculation shows that Equation (
8) can be expressed as:
where
The minimization of
f obtained from Equations (
9) and (
10) is equivalent to the minimization of the function
The minimization problem with respect to
in Equation (
11) is a semidefinite program (SDP) and therefore is a convex problem [
21]. However, the calculation of Equation (
11) as a SDP is very computationally intensive. It can be seen from Equation (
10) that a consistent estimation
can be obtained when
T tends to be infinite. Hence, the probem of minimizing
g can be reformulated as the following constrained minimization problem:
where
The minimization of the objective in Equation (
12) can be solved by means of a cyclic algorithm [
15], leading to the updated formulas of the SPICE algorithm
where index
i denotes the number of iteration. The algorithm can be initialized by means of the DAS method. The cyclic operation of the cyclic algorithm makes the objective function in Formula (
12) monotonically decrease, and the minimization process is a convex problem. Therefore, the result of SPICE algorithm has global convergence. In [
22], it is proved that the limit point of the iterative process of SPICE is the global solution of the minimization problem (
12) under the weak condition where
and
in each iteration.
4. The SPICE-ML Algorithm
SPICE algorithm has a bias in estimating the signal power, especially in the case of coherent sources (as shown in the simulation part). To solve this problem, an iteration calibration process of signal power is obtained by using AMV criterion. After applying the vectorization operator to the matrix
, we can receive the vector
where
. Note that the Gaussian circular asymptotic covariance matrix
is give by [
20]
Suppose that
can be identifiable from
. According to [
19,
20], it can be proved that the covariance matrix
is bounded below by the following real symmetric positive definite matrix
where
,
is the operation of differential. In addition, we can obtain this lower bound by minimizing the following AMV criterion
From Equations (
18) and (
20), the estimation of
and
are given by the following iterative s
where
,
. The initialization of
is provided by the SPICE algorithm. In practice the noise power
estimated by the SPICE algorithm may be different. [
23] shows that the degradation of accuracy comapared with that achieved by imposing
, is not significant. Through the iterative Formula (
21), the signal power are continuously corrected.
The estimation accuracy of the SPICE algorithm is limited to the fineness of the direction grid. A coarse grid would lead to the degradation of estimation accuracy and a problem of computational complexity arises if a high-density grid is employed. Therefore, how to choose the direction grid becomes a difficult problem. In order to overcome the limit of estimation accuracy caused by the direction grid, the DOA estimation is refined by iteratively minimizing a stochastic ML cost function.
The stochastic negative log-likelihood function of
can be expressed as [
24]
The covariance matrix of noise is defined as
Applying matrix inverse lemma to Formula (
24)
where
,
.
Then use the algebraic identity
and obtain
From Equations (
23), (
26) and (
27), we can derive
where
The ML cost function can be decomposed into two parts:
, the marginal likelihood function with parameter
excluded, and
concerning
. Therefore, the ML cost function (
23) with respect to
is equivalent to the ML function (
29). Although the calculation of multi-dimensional optimization problem is very complex, the minimization problem in Equation (
29) can be effectively solved by using the Nelder–Mead algorithm [
25]. Moreover, the Nelder–Mead algorithm has already been built into the “fminsearch” function in MATLAB. Suppose that we have obtained the corrective parameters
and
, then the refinement result can be achieved by minimizing Formula (
29).
The SPICE-ML algorithm is summarized in
Table 1.
5. Simulation Results
We evaluated the performance of the proposed SPICE-ML algorithm and compared it with DAS, IAA, and SPICE in this section. We employed a uniform linear array with 12 sensors, and the inter-element spacing was half-wavelength. The direction grid
uniformly covered the entire DOA space
with a step size of 0.5°. The SNR was defined as
where
denotes the average power of the signal. The iteration termination condition is set to
.
Three signals with power 10 dB, 8 dB, and 5 dB from
impinged on the array. The additional noise was Gaussian white noise with equal power, and the SNR is set to 20 dB. The number of snapshots was given by
. Both independent and coherent sources are shown in
Figure 2 and
Figure 3. For the case of coherent sources, the signals at
and
shared the same phases but were independent to the signal at
.
It can be seen from the simulation results of
Figure 2a and
Figure 3a, the DAS method failed to seperate the two close sources at
and
owing to the smearing effects and limited resolution. The IAA algorithm could significantly reduce the smearing effect so that the sidelobes in
Figure 2b and
Figure 3b were lower, but the resolution was still not high. The SPICE algorithm was capable of resolving the three sources, but the signal power estimated was not accurate, especially in the case of coherent sources, as shown in
Figure 2c and
Figure 3c. The SPICE-ML algorithm proposed in this paper further corrected the signal power estimated by the SPICE algorithm, leading to a more accurate signal power estimation.
Figure 2d and
Figure 3d illustrate the effectiveness and high resolution of the proposed SPICE-ML algorithm.
Next, we evaluate the root mean square error (RMSE) of DOA estimation through Monte-Carlo simulations. The defination of RMSE is:
where
is the estimated DOA of the
k signal in the
l-th Monte-Carlo trial, and
L is the total number of Monte-Carlo trials. Assume that three signals are randomly located at
. Considering both independent and coherent sources, respectively. The number of Monte-Carlo trials is 500. The RMSE curves are shown in
Figure 4 and
Figure 5. Moreover, we display the values of RMSE at each SNR and snapshot in
Table 2,
Table 3,
Table 4 and
Table 5.
From
Figure 4a,b, it can be seen that in the case of independent signal the RMSE of all algorithms decreased with the increase of SNR and snapshots, and the RMSE of SPICE-ML proposed in this paper was the lowest, which illustrates that the proposed SPICE-ML approach outperformed the other methods. From the
Table 2 and
Table 3, specifically, compared with SPICE, SPICE-ML could efficiently reduce the RMSE vs. SNR from 0.147°–0.330° to 0.022°–0.238°, the RMSE vs. snapshots from 0.065°–0.150° to 0.051°–0.113° in the case of independent signal. From
Figure 5a,b, we can see the estimation accuracy of the SPICE algorithm declined dramatically in the case of coherent signal compared with that in the case of independent signal. However, source coherence did not degrade the DAS and IAA algorithm. Notably, SPICE-ML still offered the best estimation performance in the case of coherent signal, because the angle estimated by SPICE was further refined by minimizing an ML function. From the
Table 4 and
Table 5, we can see that compared with SPICE, the RMSE vs. SNR and snapshots were reduced from 0.195°–2.777° to 0.023°–0.244°, from 0.276°–1.950° to 0.053°–0.114°, respectively. We can also observe that there existed plateau effects for DAS, IAA, and SPICE. This is because all these methods estimate DOA by means of selecting one element from a fixed set of direction grid, but there always exists an estimation bias no matter how fine the direction grid is. Theoretically, bias can be reduced by selecting a dense gird. However, a dense grid will lead to large computation cost and is not applicable in practice. On the contrary, the SPICE-ML algorithm would not suffer from the plateau effect because of a refinement DOA estimation procedure based on minimizing a ML cost function.
6. Conclusions
In this paper, we combined the SPICE DOA estimation algorithm and maximum likelihood estimation and proposed a SPICE-ML algorithm. Compared with the SPICE algorithm, the SPICE-ML method derive an iterative correction procedure for signal power estimation based on the AMV criterion, and combat the limitation of the direction grid by minimazing a Maximum Likelihood cost function. The simulation results verify the effectiveness of the proposed algorithm. In addition, the superiority of the SPICE-ML algorithm in DOA estimation accuracy is illustrated compared with the DAS, IAA, and SPICE algorithms. Specifically, comparing with SPICE, SPICE-ML can efficiently reduce the RMSE vs. SNR from 0.147°–0.330° to 0.022°–0.238° in the case of independent signal, from 0.195°–2.777° to 0.023°–0.244° in coherent signal situation, the RMSE vs. snapshots from 0.065°–0.150° to 0.051°–0.113° in the case of independent signal, from 0.276°–1.950° to 0.053°–0.114° in coherent signal situation. In the future, it will be of interest to study the performance of SPICE-ML algorithm in the case of single snapshot. This paper only considers one-dimensional DOA estimation, so another future direction of interest would be the extension of SPICE-ML to two-dimensional DOA estimation.