Laboratory Calibration and Performance Evaluation of Low-Cost Capacitive and Very Low-Cost Resistive Soil Moisture Sensors
Abstract
:1. Introduction
- What is the ability of the capacitive sensors to estimate the refractive index () of various fluids of known values?
- What empirical equation(s) can best explain the relationships between the output of the low- and very low-cost soil moisture sensor instruments tested in the study, and the actual , across a variety of soils?
- What is the difference between the respective accuracies of the soil-specific calibration equations developed in-house and the general manufacturer-provided calibration equations?
- What is the accuracy and precision performance of different low- and very low-cost soil moisture sensor instruments tested?
- How is the accuracy and precision of the developed calibration curves affected by variations in (i) temperature and (ii) electrical conductivity, within ranges that are commonly encountered in field conditions?
2. Materials and Methods
2.1. Soil Moisture Sensors
2.1.1. Capacitance Based Low-Cost Sensors: Spectrum SM100 and SMEC300
2.1.2. Generic Resistance Based Very Low-Cost Sensors: YL100 and YL69
2.1.3. Impedance-Based Sensor: Delta-T ThetaProbe ML3
2.2. Description of the Soils Used
2.3. Sensor Calibration
2.3.1. Calibration of Capacitive Sensors with Fluids
2.3.2. Calibration of Sensors with Repacked Soils
2.4. Performance Measures for the Sensors
2.4.1. Sensor Accuracy
2.4.2. Sensor Precision
2.5. Sensor Sensitivity
2.5.1. Temperature Sensitivity
2.5.2. Salinity Sensitivity
3. Results and Discussion
3.1. Sensor Calibration
3.1.1. Performance of Capacitive Sensors with Fluids
3.1.2. Calibration of All Sensors with Repacked Soils
Strength of Monotonic Relationship Between Measured () and Actual () VWC
Calibration Equations Developed between Measured () and Actual () VWC
3.1.3. Comparison of Manufacturer and In-House Calibration Equations: Capacitive Sensors
3.2. Performance Measures for the Sensors
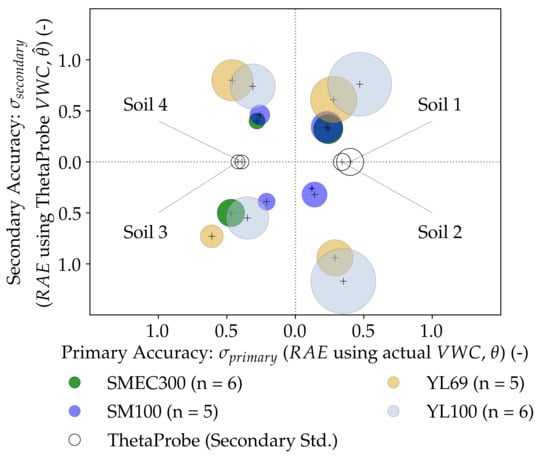
3.2.1. Sensor Accuracy
3.2.2. Sensor Precision
3.3. Sensor Sensitivity
3.3.1. Temperature Sensitivity
3.3.2. Salinity Sensitivity
3.4. Further Discussion
4. Summary and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| A/D | Analog-to-Digital value |
| EC | Electrical Conductivity |
| EM | Electromagnetic |
| FDR | Frequency Domain Reflectometry |
| IS | Indian Standard |
| LS | Least Squares (estimate) |
| MAE | Mean Absolute Error |
| RAE | Relative Absolute Error |
| RMSE | Root Mean Square Error |
| SD | Standard Deviation |
| SSR | Sum of Squared Residuals |
| TDR | Time Domain Reflectometry |
| VWC | Volumetric Water Content |
| WSN | Wireless Sensor Network |
Appendix A
| Publication | Sensor Name (Company Name) | Sensor Type | Soils Used | Calibration Curve Details |
|---|---|---|---|---|
| Paltineanu and Starr (1997) [55] | Multisensor Capacitance probe: MCAP (Enviroscan) | Capacitance sensor | Mattaplex silt loam (fine-silty, mixed, mesic, Aquic Hapludult) | Scaled frequency |
| Baumhardt et al. (2000) [69] | Multisensor Capacitance probe: MCAP (Enviroscan) | Capacitance sensor | 2 soil materials: Surface and calcic horizons of an Olton soil | Scaled frequency |
| Czarnomski et al. (2005) [35] | ECH2O (Decagon), CT 1502C (Tektronix Inc.), WCR CS615 Campbell Scientific) | Capacitance sensors | Alluvial soils of volcanic origin (sandy loam to sandy clay loam) | Linear (for capacitance sensor) |
| Sakaki et al. (2008) [70] | ECH2O (Decagon) | Capacitance sensor | 4 sands | Linear, quadratic, 2-point alpha mixing model |
| Kargas and Soulis (2012) [2] | 10HS (Decagon Devices) | Capacitance sensor | Liquids and porous media of known dielectric permittivity | 2-point calibration equation |
| Matula et al. (2016) [24] | ThetaProbe ML2x (Delta-T Devices Ltd.), ECH2O EC10 (Decagon), ECH2O EC 20 (Decagon), ECH2O EC5 (Decagon), ECH2O TE (Decagon) | Impedance sensors, FDR sensors | Silica sand and loess | Comparison between manufacturer and developed linear calibration equations |
| Kargas and Soulis (2019) [49] | CS655 (Campbell Scientific) | Water Content Reflectometer | Liquids of known dielectric permittivity and 10 soils (sand, sandy-loam, sandy-clay-loam, loam, clay-loam, clay) | 2-point, multi-point calibration equations; calibration equation for non-conductive soils using Kelleners’ method [71] |
| González-Teruel et al. (2019) [33] | Self-developed soil moisture sensor with SDI-12 communication | Capacitance based | 3 soils (clay-loams and sand) | Exponential equations |
| Category | Relevant publications |
|---|---|
| Sensor accuracy | Czarnomski et al. (2005) [35], Kargas and Soulis (2012) [2], González-Teruel et al. (2019) [33] |
| Sensor precision | Czarnomski et al. (2005) [35] |
| Sensor-to-sensor variability | Sakaki et al. (2008) [70], Rosenbaum et al. (2010) [72], Kargas and Soulis (2012) [2], Bogena et al. (2017) [3], González-Teruel et al. (2019) [33] |
| Temperature effects | Paltineanu and Starr (1997) [55], Baumhardt et al. (2000) [69], Czarnomski (2005) [35], Chanzy (2012) [58], Kargas and Soulis (2012) [2], Fares et al. (2016) [73], Bello et al. (2019) [56], Szypłowska et al. (2019) [57], Zhu et al. (2019) [74] |
| Salinity effects | Baumhardt et al. (2000) [69], Kargas and Soulis (2012) [2], Matula et al. (2016) [24], Kargas and Soulis (2019) [49] |
| Volume of influence/sensitivity | Paltineanu and Starr (1997) [55], Sakaki et al. (2008) [70], Sun et al. (2012) [75] |
| Sensor Name | Soil Type | Equation Characteristics | Segment 1 | Segment 2 |
|---|---|---|---|---|
| SMEC300 | Soil-1 | Segment limits | [1135, 1280) | [1280, 1792) |
| Slope () | 0.13 | 0.03 | ||
| Intercept () | −152.65 | −23.21 | ||
| Soil-2 | Segment limits | [1200, 1451) | 1451, 1707) | |
| Slope () | 0.07 | 0.04 | ||
| Intercept () | −85.91 | −34.23 | ||
| Soil-3 | Segment limits | [1231, 1402) | [1402, 1899) | |
| Slope () | 0.08 | 0.02 | ||
| Intercept () | −94.19 | −19.71 | ||
| Soil-4 | Segment limits | [1275, 1525) | [1525, 1685) | |
| Slope () | 0.09 | 0.00 | ||
| Intercept () | −112.50 | 23.58 | ||
| SM100 | Soil-1 | Segment limits | [1200, 1238) | [1238, 1812) |
| Slope () | 0.25 | 0.04 | ||
| Intercept () | −303.95 | −42.88 | ||
| Soil-2 | Segment limits | [1200, 1464) | [1464, 1728) | |
| Slope () | 0.07 | 0.03 | ||
| Intercept () | −87.61 | −32.15 | ||
| Soil-3 | Segment limits | [1263, 1578) | [1578, 1895) | |
| Slope () | 0.06 | 0.02 | ||
| Intercept () | −78.57 | −14.80 | ||
| Soil-4 | Segment limits | [1319, 1630) | [1630, 1833) | |
| Slope () | 0.06 | 0.01 | ||
| Intercept () | −81.29 | −3.56 | ||
| YL100 | Soil-1 | Segment limits | [2, 467.5) | [467.5, 763) |
| Slope () | 0.04 | 0.03 | ||
| Intercept () | −0.80 | 5.01 | ||
| Soil-2 | Segment limits | [6, 615.5) | [615.5, 826) | |
| Slope () | 0.03 | 0.09 | ||
| Intercept () | −0.81 | −32.32 | ||
| Soil-3 | Segment limits | [5, 333.5) | [333.5, 709) | |
| Slope () | 0.02 | 0.08 | ||
| Intercept () | −0.17 | −20.81 | ||
| Soil-4 | Segment limits | [6, 418.5) | [418.5, 705) | |
| Slope () | 0.02 | 0.07 | ||
| Intercept () | −1.08 | −21.08 | ||
| YL69 | Soil-1 | Segment limits | [11, 134) | [134, 724) |
| Slope () | 0.07 | 0.04 | ||
| Intercept () | −1.35 | 3.24 | ||
| Soil-2 | Segment limits | [7, 722] | ||
| Slope () | 0.05 | |||
| Intercept () | −0.87 | |||
| Soil-3 | Segment limits | [18, 838] | ||
| Slope () | 0.03 | |||
| Intercept () | 1.48 | |||
| Soil-4 | Segment limits | [14, 824) | ||
| Slope () | 0.03 | |||
| Intercept () | −0.71 |
References
- Gardner, W.H. Water Content. In Methods of Soil Analysis. Part 1. Physical and Mineralogical Methods, 2nd ed.; Klute, A., Ed.; American Society of Agronomy and Soil Science Society of America: Madison, WI, USA, 1986; pp. 493–544. [Google Scholar]
- Kargas, G.; Soulis, K.X. Performance analysis and calibration of a new low-cost capacitance soil moisture sensor. J. Irrig. Drain. Eng. 2012, 138, 632–641. [Google Scholar] [CrossRef]
- Bogena, H.R.; Huisman, J.A.; Schilling, B.; Weuthen, A.; Vereecken, H. Effective calibration of low-cost soil water content sensors. Sensors 2017, 17, 208. [Google Scholar] [CrossRef] [Green Version]
- Hübner, C.; Cardell-Oliver, R.; Becker, R.; Spohrer, K.; Jotter, K.; Wagenknecht, T. Wireless soil moisture sensor networks for environmental monitoring and vineyard irrigation. In Proceedings of the 8th International Conference on Electromagnetic Wave Interaction with Water and Moist Substances (ISEMA 2009), Helsinki, Finland, 1–5 June 2009; pp. 408–415. [Google Scholar]
- Ochsner, T.E.; Cosh, M.H.; Cuenca, R.H.; Dorigo, W.A.; Draper, C.S.; Hagimoto, Y.; Kerr, Y.H.; Larson, K.M.; Njoku, E.G.; Small, E.E.; et al. State of the art in large-scale soil moisture monitoring. Soil Sci. Soc. Am. J. 2013, 77, 1888–1919. [Google Scholar] [CrossRef] [Green Version]
- Robinson, D.A.; Campbell, C.S.; Hopmans, J.W.; Hornbuckle, B.K.; Jones, S.B.; Knight, R.; Ogden, F.; Selker, J.; Wendroth, O. Soil moisture measurement for ecological and hydrological watershed-scale observatories: A review. Vadose Zone J. 2008, 7, 358–389. [Google Scholar] [CrossRef] [Green Version]
- Yu, X.Q.; Wu, P.T.; Han, W.T.; Zhang, Z.L. A survey on wireless sensor network infrastructure for agriculture. Comput. Stand. Inter. 2013, 35, 59–64. [Google Scholar] [CrossRef]
- Zhang, D.J.; Zhou, G.Q. Estimation of soil moisture from optical and thermal remote sensing: A review. Sensors 2016, 46, 1308. [Google Scholar] [CrossRef] [Green Version]
- Greacen, E.L. Soil Water Assessment by the Neutron Method; Commonwealth Science Industrial Research Organization: Melbourne, Australia, 1981. [Google Scholar]
- Topp, G.C.; Davis, J.L.; Annan, A.P. Electromagnetic determination of soil water content: Measurements in coaxial transmission lines. Water Resour. Res. 1980, 16, 574–582. [Google Scholar] [CrossRef] [Green Version]
- Robinson, D.A.; Jones, S.B.; Wraith, J.M.; Or, D.; Friedman, S.P. A review of advances in dielectric and electrical conductivity measurements in soils using time domain reflectometry. Vadose Zone J. 2003, 2, 444–475. [Google Scholar] [CrossRef]
- Blonquist, J.M.; Jones, S.B.; Robinson, D.A. Standardizing characterization of electromagnetic water content sensors: Part 2. Evaluation of seven sensing systems. Vadose Zone J. 2005, 4, 1059–1069. [Google Scholar] [CrossRef]
- Fares, A.; Polyakov, V. Advances in Crop Water Management Using Capacitive Water Sensors; Sparks, D., Ed.; Elsevier Science: New York, NY, USA, 2006; pp. 43–77. [Google Scholar]
- Kojima, Y.; Shigeta, R.; Miyamoto, N.; Shirahama, Y.; Nishioka, K.; Mizoguchi, M.; Kawahara, Y. Low-cost soil moisture profile probe using thin-film capacitors and a capacitive touch sensor. Sensors 2016, 16, 1292. [Google Scholar] [CrossRef] [PubMed]
- Ojo, E.R.; Bullock, P.R.; L’Heureux, J.; Powers, J.; McNairn, H.; Pacheco, A. Calibration and evaluation of a frequency domain reflectometry sensor for real-time soil moisture monitoring. Vadose Zone J. 2015, 14, 574–582. [Google Scholar] [CrossRef]
- Gaskin, G.J.; Miller, J.D. Measurement of soil water content using a simplified impedance measuring technique. J. Agric. Eng. Res. 1996, 63, 153–159. [Google Scholar] [CrossRef]
- Noborio, K.; McInnes, K.J.; Heilman, J.L. Field measurements of soil electrical conductivity and water content by time-domain reflectometry. Comput. Electron. Agric. 1994, 11, 131–142. [Google Scholar] [CrossRef]
- Seyfried, M.S.; Murdock, M.D. Measurement of soil water content with a 50-MHz soil dielectric sensor. Soil Sci. Soc. Am. J. 2004, 68, 394–403. [Google Scholar] [CrossRef]
- Dean, T.J.; Bell, J.P.; Baty, A.J.B. Soil moisture measurement by an improved capacitance technique, Part I. Sensor design and performance. J. Hydrol. 1987, 93, 67–78. [Google Scholar] [CrossRef]
- Rijsberman, F. Can development of water resources reduce poverty? Water Policy 2003, 5, 399–412. [Google Scholar] [CrossRef]
- Srbinovska, M.; Gavrovski, C.; Dimcev, V.; Krkoleva, A.; Borozan, V. Environmental parameters monitoring in precision agriculture using wireless sensor networks. J. Clean. Prod. 2015, 88, 297–307. [Google Scholar] [CrossRef]
- Pande, S.; Savenije, H.H. A socio-hydrological model for smallholder farmers in Maharashtra, India. Water Resour. Res. 2016, 52, 1923–1947. [Google Scholar] [CrossRef]
- Den Besten, N. The socio-hydrology of smallholders in Marathwada, Maharashtra state (India). Master’s Thesis, Delft University of Technology, Delft, The Netherlands, 26 August 2016. [Google Scholar]
- Matula, S.; Bát’ková, K.; Legese, W.L. Laboratory performance of five selected soil moisture sensors applying factory and own calibration equations for two soil media of different bulk density and salinity levels. Sensors 2016, 16, 1912. [Google Scholar] [CrossRef] [Green Version]
- Cosh, M.H.; Ochsner, T.E.; McKee, L.; Dong, J.N.; Basara, J.B.; Evett, S.R.; Hatch, C.E.; Small, E.E.; Steele-Dunne, S.C.; Zreda, M.; et al. The soil moisture active passive marena, oklahoma, in situ sensor testbed (smap-moisst): Testbed design and evaluation of in situ sensors. Vadose Zone J. 2016, 15. [Google Scholar] [CrossRef] [Green Version]
- Baatz, R.; Bogena, H.R.; Franssen, H.J.H.; Huisman, J.A.; Montzka, C.; Vereecken, H. An empirical vegetation correction for soil water content quantification using cosmic ray probes. Water Resour. Res. 2015, 51, 2030–2046. [Google Scholar] [CrossRef] [Green Version]
- Bogena, H.R.; Bol, R.; Borchard, N.; Bruggemann, N.; Diekkruger, B.; Drue, C.; Groh, J.; Gottselig, N.; Huisman, J.A.; Lucke, A.; et al. A terrestrial observatory approach to the integrated investigation of the effects of deforestation on water, energy, and matter fluxes. Sci. China Earth Sci. 2015, 58, 61–75. [Google Scholar] [CrossRef]
- Qu, W.; Bogena, H.R.; Huisman, J.A.; Martinez, G.; Pachepsky, Y.A.; Vereecken, H. Effects of soil hydraulic properties on the spatial variability of soil water content: Evidence from sensor network data and inverse. Vadose Zone J. 2014, 13. [Google Scholar] [CrossRef]
- Qu, W.; Bogena, H.R.; Huisman, J.A.; Vanderborght, J.; Schuh, M.; Priesack, E.; Vereecken, H. Predicting subgrid variability of soil water content from basic soil information. Geophys. Res. Lett. 2015, 42, 789–796. [Google Scholar] [CrossRef] [Green Version]
- McBratney, A.; Whelan, B.; Ancev, T.; Bouma, J. Future directions of precision agriculture. Precis. Agric. 2005, 6, 7–23. [Google Scholar] [CrossRef]
- Martini, E.; Wollschlager, U.; Kogler, S.; Behrens, T.; Dietrich, P.; Reinstorf, F.; Schmidt, K.; Weiler, M.; Werban, U.; Zacharias, S. Spatial and temporal dynamics of hillslope-scale soil moisture patterns: Characteristic states and transition mechanisms. Vadose Zone J. 2015, 14. [Google Scholar] [CrossRef]
- Qu, W.; Bogena, H.R.; Huisman, J.A.; Vereecken, H. Calibration of a novel low-cost soil water content sensor based on a ring oscillator. Vadose Zone J. 2013, 12. [Google Scholar] [CrossRef]
- Gonzáez-Teruel, J.D.; Torres-Sánchez, R.; Blaya-Ros, P.J.; Toledo-Moreo, A.B.; Jiménez-Buendía, M.; Soto-Valles, F. Design and Calibration of a Low-Cost SDI-12 Soil Moisture Sensor. Sensors 2019, 19, 491. [Google Scholar] [CrossRef] [Green Version]
- Rosenbaum, U.; Huisman, J.A.; Vrba, J.; Vereecken, H.; Bogena, H.R. Correction of temperature and electrical conductivity effects on dielectric permittivity measurements with ECH2O sensors. Vadose Zone J. 2011, 10, 582–593. [Google Scholar] [CrossRef]
- Czarnomski, N.M.; Moore, G.W.; Pypker, T.G.; Licata, J.; Bond, B.J. Precision and accuracy of three alternative instruments for measuring soil water content in two forest soils of the Pacific Northwest. Can. J. For. Res. 2005, 35, 1867–1876. [Google Scholar] [CrossRef] [Green Version]
- Spectrum Technologies. Waterscout SM100 Soil Moisture Sensor Product Manual; Spectrum Technologies, Inc.: Plainfield, IL, USA, 2014; Available online: https://www.specmeters.com/assets/1/22/6460_SM1002.pdf (accessed on 15 March 2012).
- Spectrum Technologies. Waterscout SMEC 300 Soil Moisture Sensor Product Manual; Spectrum Technologies, Inc.: Aurora, IL, USA, 2015; Available online: https://www.specmeters.com/assets/1/22/6470_SMEC3004.pdf (accessed on 15 March 2012).
- Saleh, M.; Elhajj, I.H.; Asmar, D.; Bashour, I.; Kidess, S. Experimental evaluation of low-cost resistive soil moisture sensors. In Proceedings of the 2016 IEEE International Multidisciplinary Conference on Engineering Technology (IMCET), Beirut, Lebanon, 2–4 November 2016; pp. 179–184. [Google Scholar] [CrossRef]
- Aravind, P.; Gurav, M.; Mehta, A.; Shelar, R.; John, J.; Palaparthy, V.S.; Singh, K.K.; Sarik, S.; Baghini, M.S. A wireless multi-sensor system for soil moisture measurement. IEEE Sens. 2015, 1–4. [Google Scholar] [CrossRef]
- Bouyoucos, G.J.; Mick, A.H. A comparison of electric resistance units for making a continuous measurement of soil moisture under field conditions. Plant Physiol. 1948, 23, 532. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schmugge, T.J.; Jackson, T.J.; McKim, H.L. Survey of methods for soil moisture determination. Water Resour. Res. 1980, 16, 961–979. [Google Scholar] [CrossRef] [Green Version]
- Delta-T Devices Ltd. ThetaProbe Soil Moisture Sensor Type ML2x User Manual ML2-UM-1; Delta-T Devices: Cambridge, UK, 1999; Available online: https://www.delta-t.co.uk/wp-content/uploads/2016/11/ML2-Thetaprobe-UM.pdf (accessed on 29 August 2019).
- Miller, J.D.; Gaskin, G.J. ThetaProbe ML2x. Principles of Operation and Applications, 2nd ed.; Technical Note; UK Macaulay Land Use Research Institute: Aberdeen, UK, 1998. [Google Scholar]
- Delta-T Devices Ltd. User Manual for the ML3 ThetaProbe ML3-UM-2.1; Delta-T Devices: Cambridge, UK, 2017; Available online: https://www.delta-t.co.uk/wp-content/uploads/2017/02/ML3-user-manual-version-2.1.pdf (accessed on 29 August 2019).
- Nakra, B.C.; Chaudhry, K.K. Introduction to Instruments and Their Representation. In Instrumentation, Measurement and Analysis, 2nd ed.; Tata McGraw-Hill Publishing Company Limited: New Delhi, India, 2006; ISBN 0-07-048296-9. [Google Scholar]
- Bureau of Indian Standards (BIS). Standard Sand for Testing Cement-Specifications; IS 650:1991 (Second Revision); Bureau of Indian Standards: New Delhi, India, 2002.
- Adla, S.; Rai, N.; Harsha, K.S.; Tripathi, S.; Disse, M.; Pande, S. Laboratory Calibration of Soil Moisture Sensors in Porous Media (Repacked Soils). Available online: https://www.protocols.io/view/laboratory-calibration-of-soil-moisture-sensors-in-swnefde/metadata (accessed on 24 August 2018).
- Rosenbaum, U.; Bogena, H.R.; Herbst, M.; Huisman, J.A.; Peterson, T.J.; Weuthen, A.; Western, A.W.; Vereecken, H. Seasonal and event dynamics of spatial soil moisture patterns at the small catchment scale. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef] [Green Version]
- Kargas, G.; Soulis, K.X. Performance evaluation of a recently developed soil water content, dielectric permittivity, and bulk electrical conductivity electromagnetic sensor. Agric. Water Manag. 2019, 213, 568–579. [Google Scholar] [CrossRef]
- Starr, J.L.; Paltineanu, I.C. Methods for measurement of soil water content: Capacitance devices. In Methods of Soil Analysis: Part 4 Physical Methods; Dane, J.H., Topp, G.C., Eds.; Soil Science Society of America: Madison, WI, USA, 2002; pp. 463–474. [Google Scholar]
- Morris, A.S.; Langari, R. Instrument Types and Performance Characteristics. In Measurement and Instrumentation: Theory and Application; Butterworth-Heinemann: Oxford, UK, 2012; ISBN 9780123819604. [Google Scholar] [CrossRef]
- Carr, J.J.; Brown, J.M. Basic Theories of Measurement. In Introduction to Biomedical Equipment Technology, 4th ed.; Pearson: London, UK, 2001; ISBN 9780130104922. [Google Scholar]
- Bloom, A.J. Principles of instrumentation for physiological ecology. In Plant Physiological Ecology: Field Methods and Instrumentation, 1st ed.; Pearcy, R.W., Ehleringer, J.R., Mooney, H.A., Rundel, P.W., Eds.; Chapman and Hall: New York, NY, USA, 1989; pp. 1–12. ISBN 978-94-009-2221-1. [Google Scholar] [CrossRef]
- Compendium of Chemical Terminology, 2nd ed.; McNaught, A.D.; Wilkinson, A. (Eds.) Blackwell Scientific Publications: Oxford, UK, 1997. [Google Scholar]
- Paltineanu, I.C.; Starr, J.L. Real-time soil water dynamics using multisensor capacitance probes: Laboratory calibration. Soil Sci. Soc. Am. J. 1997, 61, 1576–1585. [Google Scholar] [CrossRef]
- Bello, Z.A.; Tfwala, C.M.; van Rensburg, L.D. Investigation of temperature effects and performance evaluation of a newly developed capacitance probe. Measurement 2019, 140, 269–282. [Google Scholar] [CrossRef]
- Szypłowska, A.; Lewandowski, A.; Jones, S.B.; Sabouroux, P.; Szerement, J.; Kafarski, M.; Wilczek, A.; Skierucha, W. Impact of soil salinity, texture and measurement frequency on the relations between soil moisture and 20 MHz–3 GHz dielectric permittivity spectrum for soils of medium texture. J. Hydrol. 2019, 579, 124155. [Google Scholar] [CrossRef]
- Chanzy, A.; Gaudu, J.C.; Marloie, O. Correcting the temperature influence on soil capacitance sensors using diurnal temperature and water content cycles. Sensors 2012, 12, 9779–9790. [Google Scholar] [CrossRef] [Green Version]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE. 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Witten, I.H.; Frank, E.; Hall, M.A. Credibility: Evaluating What’s Been Learned. In Data Mining: Practical Machine Learning Tools and Techniques, 3rd ed.; Elsevier: Burlington, MA, USA, 2011; p. 147. ISBN 978-0-12-374856-0. [Google Scholar]
- Spearman, C. The Proof and Measurement of Association between Two Things. Am. J. Psychol. 1904, 15, 72–101. [Google Scholar] [CrossRef]
- Zar, J.H. Spearman Rank Correlation. In Encyclopedia of Biostatistics; Armitage, P., Colton, T., Eds.; John Wiley & Sons, Ltd.: New York, NY, USA, 2005. [Google Scholar]
- Mukaka, M.M. A guide to appropriate use of Correlation coefficient in medical research. Malawi Med. J. 2012, 24, 69–71. [Google Scholar] [PubMed]
- Hauke, J.; Kossowski, T. Comparison of values of Pearson’s and Spearman’s correlation coefficients on the same sets of data. Quaest. Geogr. 2011, 30, 87–93. [Google Scholar] [CrossRef] [Green Version]
- Jekel, C. Fitting a Piecewise Linear Function to Data. Github Repos. 2017. Available online: https://github.com/cjekel/piecewise_linear_fit_py (accessed on 12 February 2019).
- Kinzli, K.D.; Manana, N.; Oad, R. Comparison of Laboratory and Field Calibration of a Soil-Moisture Capacitance Probe for Various Soils. J. Irrig. Drain. Eng. 2012, 138, 310–321. [Google Scholar] [CrossRef]
- Soulis, K.X.; Elmaloglou, S.; Dercas, N. Investigating the effects of soil moisture sensors positioning and accuracy on soil moisture based drip irrigation scheduling systems. Agric. Water Manag. 2015, 148, 258–268. [Google Scholar] [CrossRef]
- Vereecken, H.; Huisman, J.A.; Pachepsky, Y.; Montzka, C.; Van Der Kruk, J.; Bogena, H.; Weihermüller, L.; Herbst, M.; Martinez, G.; Vanderborght, J. On the spatio-temporal dynamics of soil moisture at the field scale. J. Hydrol. 2014, 516, 76–96. [Google Scholar] [CrossRef]
- Baumhardt, R.L.; Lascano, R.J.; Evett, S.R. Soil Material, Temperature, and Salinity Effects on Calibration of Multisensor Capacitance Probes. Soil Sci. Soc. Am. J. 2000, 64, 1940–1946. [Google Scholar] [CrossRef]
- Sakaki, T.; Limsuwat, A.; Smits, K.M.; Illangasekare, T.H. Empirical two-point α-mixing model for calibrating the ECH2O EC-5 soil moisture sensor in sands. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Kelleners, T.J.; Seyfried, M.S.; Blonquist, J.M.; Bilskie, J.; Chandler, D.G. Improved interpretation of water content reflectometer measurements in soils. Soil Sci. Soc. Am. J. 2005, 69, 1684–1690. [Google Scholar] [CrossRef]
- Rosenbaum, U.; Huisman, J.A.; Weuthen, A.; Vereecken, H.; Bogena, H.R. Sensor-to-sensor variability of the ECH2O EC-5, TE, and 5TE sensors in dielectric liquids. Vadose Zone J. 2010, 9, 181–186. [Google Scholar] [CrossRef]
- Fares, A.; Safeeq, M.; Awal, R.; Fares, S.; Dogan, A. Temperature and Probe-to-Probe Variability Effects on the Performance of Capacitance Soil Moisture Sensors in an Oxisol. Vadose Zone J. 2016, 15. [Google Scholar] [CrossRef] [Green Version]
- Zhu, Y.; Irmak, S.; Jhala, A.J.; Vuran, M.C.; Diotto, A. Time-domain and frequency-domain reflectometry type soil moisture sensor performance and soil temperature effects in fine-and coarse-textured soils. Appl. Eng. Agric. 2019, 35, 117–134. [Google Scholar] [CrossRef]
- Sun, Y.; Sheng, W.; Cheng, Q.; Chai, J.; Yun, Y.; Zhao, Y.; Xue, X.; Lammers, P.S.; Damerow, L.; Cai, X. A novel method to determine the volume of sensitivity for soil moisture sensors. Soil Sci. Soc. Am. J. 2012, 76, 1987–1991. [Google Scholar] [CrossRef]








| Measurement Technique | Soil Moisture Sensor (Company) | Price (Quotation) | Nomenclature Used in Study |
|---|---|---|---|
| Capacitance based | SMEC300 Soil Moisture, Temperature and EC sensor (Spectrum Technologies) | $219.00 | Low-cost *. |
| SM100 Soil Moisture sensor (Spectrum Technologies) | $89.00 | Low-cost. | |
| Resistance based | YL100 Soil Hygrometer Detection Module soil moisture sensor (Electronicfans) | $3.89 | Very Low-cost. |
| YL69 Generic Soil Moisture Sensor Module (Kitsguru) | $2.11 | Very Low-cost. | |
| Impedance based | ThetaProbe ML3 Soil Moisture sensor (Delta-T Devices) | $516.33 | High-cost, ‘true’ secondary standard sensor. |
| Nomenclature Used in Study | Soil Description | Bulk Density [g/cc] | Soil Texture Classification |
|---|---|---|---|
| Soil 1 | Grade I sand (1–2 mm) | 1.82 | Sand |
| Soil 2 | Grade III sand (0.09–0.5 mm) | 1.59 | Sand |
| Soil 3 | Field soil from experimental site at IIT Kanpur (Kanpur, India) | 1.23 | Silty-Loam |
| Soil 4 | Graded Silty-Loam | 1.20 | Silty-Loam |
| Fluid | at T = 25 °C [2] |
|---|---|
| Air | 1.0 |
| Butanol | 16.8 |
| Ethanol | 24.3 |
| Ethylene-glycol | 37.0 |
| De-ionized water (Water) | 81.0 |
| EC of the Water Added [mS/cm] | Actual VWC [%] | Symbolic Representation in Figure 8 |
|---|---|---|
| 1.7 | 17.8 | Circle (○) |
| 1.7 | 32.3 | |
| 1.7 | 48.81 | |
| 3.02 | 20.08 | Triangle(△) |
| 3.02 | 31.12 | |
| 3.02 | 47.32 | |
| 6.32 | 34.09 | Square(□) |
| 6.32 | 38.5 | |
| 6.32 | 49.53 | |
| 9.69 | 17.59 | Pentagon(⬠) |
| 9.69 | 34.8 | |
| 9.69 | 43.53 |
| Performance Metric | Description/Equation | Range (Ideal Value) |
|---|---|---|
| Coefficient of Determination () [59] | 0 to 1 (1) | |
| Mean Absolute Error () [60] | 0 to ∞ (0) | |
| Pooled relative standard deviation () [54] | 0 to ∞ (0) | |
| Relative Absolute Error () [60] | 0 to ∞ (0) | |
| Root Mean Squared Error () [60] | 0 to ∞ (0) | |
| 0 to ∞ (0) | ||
| between in-house calibrated and actual value | 0 to ∞ (0) | |
| between in-house calibrated and ThetaProbe value | 0 to ∞ (0) | |
| Spearman’s Rank Correlation Coefficient () [61] | −1 to 1 (−1 or 1) |
| SMEC300 | SM100 | ThetaProbe | |
|---|---|---|---|
| 0.87 | 0.55 | 0.48 | |
| 0.22 | 0.27 | 0.24 | |
| 1.08 | 0.74 | 0.75 | |
| 0.0062 | 0.0062 | 0.0405 |
| Low-Cost | Very Low-Cost | |||
|---|---|---|---|---|
| Capacitive Sensors | Resistive Sensors | |||
| SMEC300 | SM100 | YL100 | YL69 | |
| Soil 1 | 0.93 | 0.92 | 0.78 | 0.91 |
| Soil 2 | 0.96 | 0.97 | 0.89 | 0.94 |
| Soil 3 | 0.84 | 0.94 | 0.94 | 0.73 |
| Soil 4 | 0.95 | 0.92 | 0.94 | 0.85 |
| Average | 0.92 | 0.94 | 0.89 | 0.86 |
| Low-Cost Capacitive Sensors | Very Low-Cost Resistive Sensors | Secondary Standard | |||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SMEC300 | SM100 | YL100 | YL69 | ThetaProbe | |||||||||||||||||
| Manufacturer Calibration | In-house Calibration | Manufacturer Calibration | In-house Calibration | In-house Calibration | In-house Calibration | Manufacturer Calibration | |||||||||||||||
| MAE | RMSE | RAE | MAE | RMSE | RAE | MAE | RMSE | RAE | MAE | RMSE | RAE | MAE | RMSE | RAE | MAE | RMSE | RAE | MAE | RMSE | RAE | |
| Soil 1 | 9.63 | 11.76 | 1.01 | 2.28 | 3.34 | 0.24 | 8.17 | 10.22 | 0.84 | 2.27 | 2.97 | 0.23 | 4.31 | 5.88 | 0.47 | 2.58 | 3.53 | 0.28 | 3.79 | 4.84 | 0.40 |
| Soil 2 | 7.13 | 8.63 | 0.89 | 0.96 | 1.39 | 0.12 | 6.75 | 8.23 | 0.87 | 1.12 | 1.63 | 0.14 | 3.42 | 4.54 | 0.35 | 2.95 | 3.90 | 0.29 | 2.88 | 4.46 | 0.34 |
| Soil 3 | 7.17 | 9.99 | 1.00 | 3.33 | 4.20 | 0.47 | 5.82 | 7.74 | 0.80 | 1.54 | 2.55 | 0.21 | 3.41 | 5.99 | 0.35 | 6.38 | 8.09 | 0.61 | 2.98 | 4.29 | 0.39 |
| Soil 4 | 6.44 | 7.90 | 0.96 | 1.90 | 2.61 | 0.28 | 4.18 | 5.27 | 0.63 | 1.74 | 2.27 | 0.26 | 2.90 | 4.45 | 0.31 | 4.60 | 6.65 | 0.46 | 3.07 | 4.23 | 0.42 |
| Average | 7.59 | 9.57 | 0.97 | 2.12 | 2.88 | 0.28 | 6.23 | 7.86 | 0.78 | 1.67 | 2.36 | 0.21 | 3.51 | 5.21 | 0.37 | 4.13 | 5.54 | 0.41 | 3.18 | 4.45 | 0.39 |
| Low-Cost | Very Low-Cost | Secondary | |||
|---|---|---|---|---|---|
| Capacitive Sensors | Resistive Sensors | Standard | |||
| SMEC300 | SM100 | YL100 | YL69 | ThetaProbe | |
| Soil 1 | 0.51 | 0.55 | 1.11 | 0.81 | 0.47 |
| Soil 2 | 0.05 | 0.44 | 1.13 | 0.63 | 0.30 |
| Soil 3 | 0.48 | 0.30 | 0.74 | 0.40 | 0.24 |
| Soil 4 | 0.28 | 0.35 | 0.78 | 0.72 | 0.24 |
| Average | 0.33 | 0.41 | 0.94 | 0.64 | 0.31 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Adla, S.; Rai, N.K.; Karumanchi, S.H.; Tripathi, S.; Disse, M.; Pande, S. Laboratory Calibration and Performance Evaluation of Low-Cost Capacitive and Very Low-Cost Resistive Soil Moisture Sensors. Sensors 2020, 20, 363. https://doi.org/10.3390/s20020363
Adla S, Rai NK, Karumanchi SH, Tripathi S, Disse M, Pande S. Laboratory Calibration and Performance Evaluation of Low-Cost Capacitive and Very Low-Cost Resistive Soil Moisture Sensors. Sensors. 2020; 20(2):363. https://doi.org/10.3390/s20020363
Chicago/Turabian StyleAdla, Soham, Neeraj Kumar Rai, Sri Harsha Karumanchi, Shivam Tripathi, Markus Disse, and Saket Pande. 2020. "Laboratory Calibration and Performance Evaluation of Low-Cost Capacitive and Very Low-Cost Resistive Soil Moisture Sensors" Sensors 20, no. 2: 363. https://doi.org/10.3390/s20020363
APA StyleAdla, S., Rai, N. K., Karumanchi, S. H., Tripathi, S., Disse, M., & Pande, S. (2020). Laboratory Calibration and Performance Evaluation of Low-Cost Capacitive and Very Low-Cost Resistive Soil Moisture Sensors. Sensors, 20(2), 363. https://doi.org/10.3390/s20020363