1. Introduction
Nitrate (NO
3−) and nitrite (NO
2−) ions are the most common forms of inorganic nitrogen found in environmental samples [
1,
2]. The abundance and distribution of these species in surface water are often characterized by hydrological regime, seasonal changes, spatial and temporal variability, and the mode and nature of the nutrient sources [
1]. They are regulated pollutants, and drinking water treatment may be required to reduce their level within the regulated limits. Nitrification is a common issue observed in drinking water disinfected by monochloramine (NH
2Cl) [
3,
4]. This is a microbiological process where free ammonia (NH
3), released through monochloramine decomposition, is converted to nitrite and nitrate by nitrifying bacteria, resulting in elevated concentrations of these species in water [
3,
5]. Drinking water containing high levels of nitrate and nitrite may pose threats to public health. The World Health Organization suggests that the maximum contaminant level (MCL) of nitrate and nitrite in drinking water should not exceed 11.3 mg L
−1 as NO
3-N, and 0.9 mg L
−1 as NO
2-N [
6,
7]. Fast and rapid detection of nitrate and nitrite is required to minimize the risk of nitrification, and to ensure the regulatory compliance [
8].
Analytical methods used to determine nitrate and/or nitrite include colorimetry, potentiometry, spectrophotometry, spectrofluorimetry, chromatography, etc. [
9,
10]. Over many years, optical techniques have been successfully used to measure a range of water quality parameters, including dissolved organic carbon (DOC), nitrate, nitrite, and monochloramine, with an excellent limit of detection [
11,
12,
13,
14]. Singh et al. [
2] reviewed various spectroscopic methods and concluded that UV-Vis spectrophotometry is widely accepted because of its simplicity, feasibility, and versatility. Evidence described in the literature suggests that inorganic nitrate and nitrite ions dissolved in water strongly absorb UV light, with a high correlation between concentration and absorption spectra [
1,
8,
13,
15,
16]. The inherent absorption properties of nitrate and nitrite will make it possible to detect them using the spectrophotometric method without using any reagents [
13]. For nitrite, the absorption peak appears around 213 nm, whereas for nitrate, different wavelengths for absorption peak are reported that vary by concentration [
16,
17]. The absorption peak of nitrate gradually shifts to the right as the concentration increases. Karlsson et al. [
8] reported that nitrate has an absorption peak at 205 nm wavelength. A similar study reported that nitrate has a primary and secondary peak at 202 nm and 302 nm, respectively. In contrast, for nitrite, the primary and secondary peaks appeared at 210 nm and 355 nm, respectively [
11]. However, at a low level of nitrate and nitrite usually produced in typical chloraminated drinking water during nitrification, the secondary peak is unsuitable to detect and measure because of the inadequate response at that wavelength. Measuring them using the primary peak is also often disturbed by interference by other organic and inorganic substances that absorb UV light within the primary peak region. As both nitrate and nitrite absorb UV light in the same wavelength range, the global NO
x− concentration (combined NO
2− + NO
3−) is sometimes preferred to avoid the difficulties associated with discriminating between nitrate and nitrite [
13].
Several studies have reported the application of different data analytic techniques for the determination of nitrate and nitrite using single or multi-wavelength absorption spectra [
1,
8,
11,
13,
15,
17,
18,
19,
20,
21,
22]. For instance, Karlsson et al. [
8] used multivariate data analysis to relate spectra and concentrations of municipal wastewater. A different approach was proposed by Jiao et al. [
15] who used the secondary absorption peak to link spectra and nitrite content in environmental samples. Using multiple linear regression, they assessed the effect of pH on regression performance, where the best modelling performance was achieved at a pH of 5 or greater because the component of aqueous solution of nitrite depends on the pH value. When the pH is 5 or above, the solutions contain more than 99% of nitrite, whereas if the pH is 1.1 or below, the solution contains more than 99% of nitrous acid (HONO) [
23]. The second derivative of absorbance (SDA) is also widely used to resolve the overlapping peaks, and to enhance the signal [
1,
24]. Based on the SDA method, Ferree and Shannon [
19] measured the nitrate content in wastewater samples, whereas Causse et al. [
1] assessed the SDA at 226 nm to determine the same in raw waters. Similarly, Pons et al. [
22] assessed a range of river water samples and found good linear correlation between the maxima of the SDA and the corresponding nitrate concentrations. In typical drinking water, natural organic matter (NOM) absorbs a significant portion of UV light, causing major interference towards the measurement of nitrate and nitrite. Hence, using more than one wavelength, where both nitrate and nitrite do not absorb, can improve the measurement accuracy. Edwards et al. [
25] proposed absorbance measurements at 205 nm and 300 nm to determine nitrate content in the presence of NOM. Huebsch et al. [
17] evaluated the double and multi-wavelength spectrophotometric measurements using partial least square regression (PLSR) for monitoring nitrate in groundwater samples. These studies suggested that UV-Vis spectrophotometry coupled with various data analytic techniques can be used as a powerful tool to measure the nitrate, nitrite, or combined NO
x− concentrations in water from various sources, including drinking water, river water, waste water, etc.
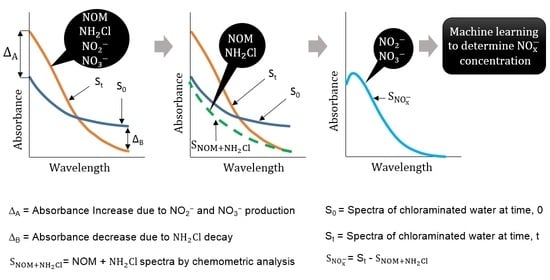
When a chloraminated sample undergoes nitrification, significant changes in various water quality parameters are evident [
3,
4]. This includes a decrease in monochloramine concentration, an increase in NO
x− production, and an initial increase of ammonia concentration followed by a decrease. The water quality change suggests that the method needs to be sensitive, such that changes in NO
x− and monochloramine as a result of nitrification can be detected. Theoretically, the NOM concentration, measured as dissolved organic carbon (DOC), should also change. However, the change of DOC concentration over time is relatively slow and small in magnitude, whereas ammonia has little or no UV absorbances under the typical range of concentration found in drinking water. Hence, the contribution of NOM and ammonia to change the spectra can be ignored. When no monochloramine residual is left in water, the NO
x− production between two timestamps, t = 0 and t = t, is related to the NO
x− spectra, which can be simply obtained by subtracting the spectra at t = 0 from the spectra at t = t. However, if there is monochloramine residual left in water, the spectra difference between two timestamps does not represent the whole NO
x− spectra, as monochloramine has absorbance within the range absorbed by NO
x− species. In this case, an additional spectral compensation is required to modify the spectra interfered by monochloramine absorbances. This study proposes such a spectral compensation to account the monochloramine absorbance, based on the behavior of pure monochloramine spectra. Hence, the objectives of this study are: (i) to isolate the NO
x− spectra from the total spectra; and (ii) to determine the NO
x− concentrations using standard data analytic techniques. This method works on determining the relative NO
x− production between two timestamps, hence, it is suitable to use when there is no additional information of lab NO
x− is available. This is a novel method, as no previous studies offer a similar approach to what is proposed in this paper. Hence, this paper provides a significant new knowledge contribution to manage nitrification in drinking water systems.
3. Results
The average water quality parameters at the TB-WTP and the selected location of the distribution system (Meningie) are presented in
Table 1. These values were obtained through grab sample analysis at the laboratory.
As shown in
Table 1, most water quality parameters, including pH, turbidity, DOC, free chlorine and dichloramine concentrations, are similar at both locations. However, monochloramine, free ammonia and NO
x− concentrations vary significantly. For instance, the typical monochloramine concentration at the WTP is 4.10 ± 0.30 mg L
−1, whereas at Meningie, the concentration drops to 1.60 ± 1.0 mg L
−1. A significant amount of monochloramine residual is lost along the way to Meningie. At the same time, free ammonia and NO
x− concentrations at Meningie also increased. Decreased monochloramine residual and increased free ammonia and NO
x− concentrations show the incidences of nitrification at Meningie several times in the past years.
The typical monochloramine spectra presented in
Figure 4a shows the UV absorbances in Milli-Q water of up to 300 nm for concentrations ranging from 0.2 mg L
−1 to 5.0 mg L
−1. Water utilities usually practice chloramination within that range. The remaining region of the spectra is relatively flat and not shown. The peak absorption appeared at 245 nm wavelength, which aligns with many previous studies [
14,
27]. For all concentrations tested, the spectra were very symmetric, with a high correlation between concentrations and absorbances at 245 nm wavelength observed. For the formation of monochloramine in Milli-Q water, the pH was initially adjusted to 9 to minimize the formation of dichloramine, as a relatively high pH can potentially reduce the dichloramine formation [
32,
33]. Consequently, the interference by the dichloramine spectra was the minimum. A relatively high pH value also ensured no significant monochloramine autodecomposition occurred during the course of the experiment [
32]. After chloramination, the measured dichloramine concentration was less than 0.1 mg L
−1. Therefore, the spectra obtained were assumed to be the pure monochloramine spectra without any significant interference by dichloramine. As the pH of chloraminated drinking water samples can vary throughout the distribution system, the pure monochloramine spectra were also investigated for two other pH of 8 and 7. Using the spectral data at various pH combinations allows a reliable estimate to be determined for a range of values at an unknown pH. However, no significant differences were found in absorbance spectra between pH values of 7 and 9.
As can be seen in
Figure 4a, the spectra are very symmetric about the concentrations, hence, the absorbance differences (∆
I,ultrapure) for two different monochloramine concentrations at various wavelengths can be related to each other by some functions. Newly composed R programming codes were used to calculate ∆
i,ultrapure for all possible combinations of concentrations at each wavelength from 200 nm to 245 nm. The wavelength 245 nm was chosen because monochloramine peak absorption wavelength approximately appears at 245 nm, hence, maximum absorbance difference (∆
max) is expected at that wavelength (∆
max,ultrapure = ∆
245,ultrapure). Therefore, expressing ∆
i,ultrapure as a function of ∆
245,ultrapure will encounter a relatively lower error in regression. Moreover, typical nitrate and nitrite spectra do not have significant UV absorbances beyond 245 nm. The relationship between ∆
i,ultrapure and ∆
245,ultrapure can be determined by plotting these data and fitting the standard trend line.
Figure 4b shows the plot of ∆
i,ultrapure against ∆
245,ultrapure at many intermediate wavelengths from 240 nm to 200 nm with a 5 nm increment. The trend lines in these plots indicate that there is a linear association between ∆
i,ultrapure and ∆
245,ultrapure.
Figure 4c shows the R
2 and RMSE values in the linear model fit, where it is evident that the value of R
2 gradually improved, and RMSE decreased towards 245 nm. The lowest R
2 obtained in the linear model fit was greater than 0.93, which indicates that the variable ∆
245,ultrapure can adequately predict the ∆
i,ultrapure with a good level of accuracy. The full range of R
2 and RMSE values between 200 nm and 244.5 nm is presented in
Table A1 in
Appendix A.
The recorded spectra for samples1–6 during a period of eight weeks is shown in
Figure 5. For each sample, the initial spectra (t = 0) were considered as baseline. As can be seen in
Figure 5, the absorbances at 245 nm decreased in all samples over time due to monochloramine decay, whereas it increased between 200 nm and 225 nm due to nitrate and nitrite productions. All sample spectra intersect their baseline spectra at approximately 220 nm, which also indicated that, except monochloramine, there are absorbances by other species involved in the spectra, which was nitrate and nitrite. Due to the monochloramine decay effect, the whole spectra will shift proportionally downward throughout 200 nm to 245 nm, and will not cross the baseline. The highest variability in spectral configuration was found in the enhanced samples (Sample3 and Sample6). The starting monochloramine concentration of these samples were 4.3 mg L
−1 at the TB-WTP site (Samples1–3) and 1.3 mg L
−1 at the Meningie site (Samples4–6), respectively. Nitrification was observed in Sample6, where a significant increase in UV absorbance was evident. It is possible that Sample3 did not experience nitrification because its initial monochloramine concentration was relatively higher compared to that of Sample6. Thus, the microbial inactivation rate by monochloramine was also much higher compared to their growth rate. On the other hand, Sample4 and Sample5 have near similar spectral changes around the 245 nm region, but different level of changes in between 200 nm and 225 nm, indicating different levels of NO
x− productions in these samples. This suggests that NO
x− production is related to a number of factors, including initially available ammonia, the production of additional ammonia through monochloramine decomposition, and the rate of ammonia conversion to NO
x−.
With regard to the baseline, the absorbance difference at 245 nm wavelength, ∆
245, sample, was calculated for each sample, which was then used to predict the ∆
i, sample values using the linear functions between ∆
245, ultrapure and ∆
i, ultrapure. This produces a dataset of n − 1 sets of ∆
200–245 values for n number of spectra at each sample. These estimated ∆
i, sample values were subtracted from their baseline values to estimate the spectra change caused by the monochloramine decay only.
Figure 6 shows the estimated spectra for the six samples, where the topmost spectra are the baseline. It is evident in the figure that spectra sets in Samples1–3 (
Figure 6a–c) have much downward shift compared to that observed in Samples3–6 (
Figure 6d–f). This is because initial monochloramine concentration of Samples1–3 was much higher compared to Samples3–6, hence, more absorbance reduction occurred in these samples because of monochloramine decay during the study period.
For all samples, the spectra in
Figure 6 were subtracted from the spectra in
Figure 5 to obtain the NO
x− spectra that includes both nitrate and nitrite absorbances. The isolated NO
x− spectra presented in
Figure 7 show that the enhanced samples (Sample3 and Sample6) have the maximum UV absorbances, suggesting that the production of nitrate and nitrite are the maximum in these samples. This is because the ammonia concentration was increased in these samples to encourage microbiological activity, resulting in an increased conversion of ammonia to nitrate and nitrite. Further, some spectra in Sample6 showed an increase in absorbance compared to other samples by several orders of magnitude, suggesting that severe nitrification occurred. In contrast, the NO
x− spectra in filtered samples (Sample2 and Sample5) have the lowest absorbance response, hence, nitrification was absent in these samples because microbiological activity was reduced by filtering these samples. Compared to filtered and enhanced samples, the unprocessed samples (Sample1 and Sample4) have an intermediate level of NO
x− production. The isolated NO
x− spectra closely resemble the typical NO
x− spectra in Milli-Q water.
The estimated NO
x− spectra presented in
Figure 7 were passed to the machine learning model developed using the SVR algorithm to predict the relative NO
x− concentrations. For this purpose, nitrate and nitrite solutions of known concentrations were mixed to form several combinations, and the corresponding NO
x− spectra were acquired and used in model training.
Figure 8a–e shows the individual nitrite, nitrate, and mixed NO
x− spectra at various concentrations in Milli-Q water, where it is evident that for the same concentration, nitrate has a relatively higher absorbance than nitrite. The peak absorption of nitrite spectra appears at 210 nm, which is approximately symmetric with respect to concentration (
Figure 8a). On the other hand, the peak absorption for nitrate spectra starts from 205 nm and gradually shifts to the right as the concentration increases (
Figure 8b). For a relatively high concentration of nitrite and nitrate (over 10 mg-N L
−1), a secondary peak was visible at 302 nm and 355 nm, respectively (
Figure 8c,d). However, for low concentrations (below 10 mg-N L
−1), the UV absorption at the secondary peak region is inadequate, hence, they cannot be effectively applied to quantify the low level of nitrite and nitrate usually encountered in drinking water during nitrification. Spectral analysis suggests that the shape of the NO
x− spectra is primarily dominated by the nitrate concentration, as it has a relatively higher absorbance compared to nitrite (
Figure 8e). Using the NO
x− spectra as predictor variables, and corresponding concentrations as response variables, the SVR model requires a fine tune of the two parameters. The parameter C represents the penalty for misclassified data points, whereas the parameter
controls the curvature of the decision boundary. They were obtained by the grid search method, and the RBF kernel was used to map the data. Using a 10-fold cross-validation, the performance of the SVR model, in terms of R
2 in model training and cross-validation, was over 0.99, with RMSE < 0.04, which indicates a satisfactory relationship between spectra and concentration. The final parameters of the SVR model are presented in
Table A2 in
Appendix A. The developed SVR model was used to predict the NO
x− concentrations in the six samples using the separated NO
x− spectra presented in
Figure 7.
The estimated NO
x− concentration by the proposed method is shown in
Figure 9a, and the numeric values are presented in
Table A3 in
Appendix A. The NO
x− values in the figure represent the relative NO
x− concentration with respect to the baseline values, as the initial NO
x− content in the baseline spectra was set to zero. Therefore, the total NO
x− concentration would be the sum of initial NO
x− content in the baseline spectra plus relative NO
x− content estimated by the method. In
Figure 9a, Samples 1–3 show an increasing trend in NO
x− production, whereas Samples 4–5 show an initial increase, followed by either a stable or decreasing trend. On the other hand, the trend of Sample6 shows a sharp rise in NO
x− concentration, indicating a nitrification episode. Overall, the estimated NO
x− concentrations for all samples closely reflect their spectra presented in
Figure 7. The proposed method was validated against the lab NO
x− data (
Appendix A,
Table A4 and
Table A5), and a good level of agreement was found between them.
Figure A1 in
Appendix A compares the estimated relative NO
x− concentration by the proposed method and the relative NO
x− concentrations calculated from the lab data.
Figure 9b shows a strong linear relationship (R
2 = 0.83) between the estimated and the lab data. The trend-line equation represents the local calibration function to relate the lab data with the model predicted values. Some inaccuracies may be encountered during the estimation of the ∆
i, sample and corresponding NO
x− spectra by the linear models. Also, if the time difference between the spectra fingerprint and the lab test result varies, local calibration performance can be poor.
The literature and the guidance manuals of many water utilities suggest that changes in nitrite by 0.05 mg-N L
−1 or above gives an indication of nitrification [
34]. The proposed method tracks the change of relative NO
x− concentration, hence, a value around 0.05 mg-N L
−1 indicates either an increased level of nitrite or nitrate or both. In such a case, further investigation is required to ensure the status of nitrification.
4. Discussion
The spectrophotometric method proposed in this paper can be implemented by the drinking water industry to monitor nitrification activity throughout the network. Implementing this method online will require regular changing of the baseline to cope with the incoming water. In a drinking water distribution system, the quality of water and spectral characteristics change continuously, depending on source and treatment characteristics. To obtain more accurate estimates of NOx−, a local calibration using site-specific water quality data is recommended. The accuracy of the laboratory measurements may also be subject to errors from various sources, including measurement range, analysis method, human errors in grab sampling, etc. This is a critical part, as the accuracy of the method is highly affected by the level of calibration. Therefore, calibration using good water quality data is required to obtain a better accuracy by the proposed method.
The lab UV-Vis fingerprint was obtained by filtering the sample through 0.45 μm filter paper to remove the particle absorbances. However, in recent years, several chemometric techniques have been developed to do the particle compensation [
14,
35]. It is recommended to compare both methods to improve the particle compensation. The chemometric particle compensation techniques could be possibly incorporated into the method proposed in this paper to develop an automated nitrification monitoring system. This could be an area to investigate further.
It was assumed that the absorbance reduction at 245 nm was entirely caused by monochloramine decay. However, at that wavelength, NOM may contribute towards absorbance reduction. As shown in
Figure 10, monochloramine decay during the study period was much faster than the decrease of organic concentration (measured as DOC), which was ≤ 0.2 mg L
−1. When this method is employed within a short period (usually less than a week), spectra change due to organic absorbance at 245 nm can be considered to be zero. Therefore, this method works well within a short period. Otherwise, if the DOC concentration is available, it can be used to quantify the absorbance reduction by NOM, since DOC is reported to have an excellent correlation to UV absorbances. Moreover, due to monochloramine autodecomposition, free ammonia is produced, which may also absorb UV light. The spectral analysis of the pure ammonia solution indicated that it has little or no UV absorbances when appearing in a relatively low concentration, usually found in drinking water systems (up to 5 mg L
−1 as NH
3-N).
The spectral fingerprints were taken using a 10 cm optical pathlength cell, and the maximum NOx− concentration used to build the SVR model was 2.4 mg-N L−1 (1.2 mg-N L−1 of nitrite + 1.2 mg-N L−1 of nitrate), hence, the method works well within that limit. Beyond that limit, the instrument sensitivity may affect the measurement accuracy. If a high concentration of nitrate and nitrite are expected, it is recommended to use a short pathlength cell. Also, it was assumed that the major light-absorbing species in the spectra were NOM, nitrate, nitrite, and monochloramine, which are common in most typical drinking waters. No chemical reaction between these species, or absorbance increase/decrease due to their internal reactions, were considered. For a relatively short time duration between the baseline and the subsequent spectra, the internal reactions and their effects on the spectra can be negligible. If other UV light-absorbing species exist in the spectra, the accuracy of the method may differ due to the interferences by these species. Further study is required to confirm this.
Currently, UV spectrophotometry has been increasingly used for online monitoring of various water quality parameters [
1]. Among the various methods of nitrification monitoring, spectroscopic methods are preferable because of their simplicity, rapid detection, and high sensitivity, which improves the accuracy of detection [
2,
36]. To develop online based sensors, Banna et al. [
37] indicated important criteria, including response, measurement range, sensitivity, accuracy, lifetime, maintenance, and cost, need to be considered. The proposed method has a rapid response with high sensitivity and good accuracy, hence, it can be used to develop an online nitrification monitoring system. Unlike many other UV-based methods of nitrate/nitrite monitoring of environmental samples which use oxidizing or complexing agents, this method is simple and does not require any chemical addition. Compared to other methods, such as SDA, the incorporated spectral compensation for monochloramine absorbance makes it more compatible for monitoring rapid chloramine decay and nitrification in chloraminated systems. By incorporating the online monitoring to the proposed method, an early warning system can be developed that will help to prevent nitrification in drinking water distribution systems. This could be an area to explore further.