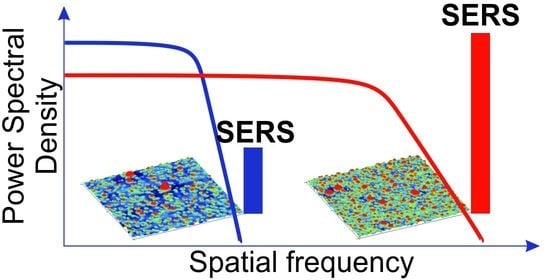
Power Spectral Density Analysis for Optimizing SERS Structures
Abstract
:1. Introduction
2. Materials and Methods
2.1. Power Spectral Density Analysis
2.2. Developed Model
2.3. Experimental
3. Results and Discussion
3.1. Experimental
3.1.1. Electrodynamic Modeling
3.1.2. Modeling of PSD and Raman Enhancement
3.2. Experimental Studies
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Wei, H.; Hossein Abtahi, S.M.; Vikesland, P.J. Plasmonic colorimetric and SERS sensors for environmental analysis. Environ. Sci. Nano 2015, 2, 120–135. [Google Scholar] [CrossRef] [Green Version]
- Saleh, T.A. Pharmaceutical Characterization and Detection Using Surface-Enhanced Raman Scattering. Int. Arch. Clin. Pharmacol. 2017, 3, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Vo-Dinh, T. SERS chemical sensors and biosensors: New tools for environmental and biological analysis. Sens. Actuators B Chem. 1995, 29, 183–189. [Google Scholar] [CrossRef]
- Ma, Y.; Promthaveepong, K.; Li, N. Chemical Sensing on a Single SERS Particle. ACS Sens. 2017, 2, 135–139. [Google Scholar] [CrossRef]
- Ko, E.; Hwang, J.; Kim, J.H.; Lee, J.H.; Lee, S.H.; Tran, V.-K.; Sung, C.W.; Park, C.H.; Choo, J.; Seong, G.H. Electrochemical Fabrication of Nanostructures on Porous Silicon for Biochemical Sensing Platforms. Anal. Sci. 2016, 32, 681–686. [Google Scholar] [CrossRef] [Green Version]
- Chen, H.-C.; Chen, C.-H.; Hsu, C.-S.; Chen, T.-L.; Liao, M.-Y.; Wang, C.-C.; Tsai, C.-F.; Chen, H.M. In Situ Creation of Surface-Enhanced Raman Scattering Active Au–AuO x Nanostructures through Electrochemical Process for Pigment Detection. ACS Omega 2018, 3, 16576–16584. [Google Scholar] [CrossRef] [Green Version]
- Gao, J.; Zhang, N.; Ji, D.; Song, H.; Liu, Y.; Zhou, L.; Sun, Z.; Jornet, J.M.; Thompson, A.C.; Collins, R.L.; et al. Superabsorbing Metasurfaces with Hybrid Ag-Au Nanostructures for Surface-Enhanced Raman Spectroscopy Sensing of Drugs and Chemicals. Small Methods 2018, 2, 1800045. [Google Scholar] [CrossRef]
- Yoon, H.; Suh, J.S. Universal substrates based on Ag colloidal particles for routine surface-enhanced Raman scattering spectral measurements. RSC Adv. 2017, 7, 28573–28579. [Google Scholar] [CrossRef] [Green Version]
- Le Ru, E.C.; Etchegoin, P.G. Quantifying SERS enhancements. MRS Bull. 2013, 38, 631–640. [Google Scholar] [CrossRef]
- Hayashi, S. SERS on random rough silver surfaces: Evidence of surface plasmon excitation and the enhancement factor for copper phthalocyanine. Surf. Sci. 1985, 158, 229–237. [Google Scholar] [CrossRef]
- Tian, Z.-Q.; Ren, B.; Wu, D.-Y. Surface-Enhanced Raman Scattering: From Noble to Transition Metals and from Rough Surfaces to Ordered Nanostructures. J. Phys. Chem. B 2002, 106, 9463–9483. [Google Scholar] [CrossRef]
- Aroca, R.; Martin, F. Tuning metal island films for maximum surface-enhanced Raman scattering. J. Raman Spectrosc. 1985, 16, 156–162. [Google Scholar] [CrossRef]
- Zhurikhina, V.V.; Brunkov, P.N.; Melehin, V.G.; Kaplas, T.; Svirko, Y.; Rutckaia, V.V.; Lipovskii, A.A. Self-assembled silver nanoislands formed on glass surface via out-diffusion for multiple usages in SERS applications. Nanoscale Res. Lett. 2012, 7, 676. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, Y.; Yang, C.; Xue, B.; Peng, Z.; Cao, Z.; Mu, Q.; Xuan, L. Highly effective and chemically stable surface enhanced Raman scattering substrates with flower-like 3D Ag-Au hetero-nanostructures. Sci. Rep. 2018, 8, 898. [Google Scholar] [CrossRef] [Green Version]
- Cheng, Z.; Qiu, Y.; Li, Z.; Yang, D.; Ding, S.; Cheng, G.; Hao, Z.; Wang, Q. Fabrication of silver dendrite fractal structures for enhanced second harmonic generation and surface-enhanced Raman scattering. Opt. Mater. Express 2019, 9, 860. [Google Scholar] [CrossRef]
- Babich, E.; Raskhodchikov, D.; Redkov, A.; Hmima, A.; Nashchekin, A.; Lipovskii, A. Dendritic structures by glass electrolysis: Studies and SERS capability. Curr. Appl. Phys. 2021, 24, 54–59. [Google Scholar] [CrossRef]
- Batista, E.; dos Santos, D.; Andrade, G.S.; Sant’Ana, A.; Brolo, A.; Temperini, M.A. Using Polycarbonate Membranes as Templates for the Preparation of Au Nanostructures for Surface-Enhanced Raman Scattering. J. Nanosci. Nanotechnol. 2009, 9, 3233–3238. [Google Scholar] [CrossRef]
- Miller, E.N.; Palm, D.C.; De Silva, D.; Parbatani, A.; Meyers, A.R.; Williams, D.L.; Thompson, D.E. Microsphere Lithography on Hydrophobic Surfaces for Generating Gold Films that Exhibit Infrared Localized Surface Plasmon Resonances. J. Phys. Chem. B 2013, 117, 15313–15318. [Google Scholar] [CrossRef]
- Abu Hatab, N.A.; Oran, J.M.; Sepaniak, M.J. Surface-Enhanced Raman Spectroscopy Substrates Created via Electron Beam Lithography and Nanotransfer Printing. ACS Nano 2008, 2, 377–385. [Google Scholar] [CrossRef]
- De Silva Indrasekara, A.S. Design criteria to fabricate plasmonic gold nanomaterials for surface-enhanced Raman scattering (SERS)-based biosensing. J. Appl. Phys. 2021, 129, 231102. [Google Scholar] [CrossRef]
- Lin, X.-M.; Cui, Y.; Xu, Y.-H.; Ren, B.; Tian, Z.-Q. Surface-enhanced Raman spectroscopy: Substrate-related issues. Anal. Bioanal. Chem. 2009, 394, 1729–1745. [Google Scholar] [CrossRef] [Green Version]
- Bai, S.; Sugioka, K. Recent Advances in the Fabrication of Highly Sensitive Surface-Enhanced Raman Scattering Substrates: Nanomolar to Attomolar Level Sensing. Light Adv. Manuf. 2021, 2, 1–25. [Google Scholar] [CrossRef]
- Shiohara, A.; Wang, Y.; Liz-Marzán, L.M. Recent approaches toward creation of hot spots for SERS detection. J. Photochem. Photobiol. C Photochem. Rev. 2014, 21, 2–25. [Google Scholar] [CrossRef]
- Babich, E.; Scherbak, S.; Asonkeng, F.; Maurer, T.; Lipovskii, A. Hot spot statistics and SERS performance of self-assembled silver nanoisland films. Opt. Mater. Express 2019, 9, 4090. [Google Scholar] [CrossRef]
- Norton, M.P.; Karczub, D.G. Fundamentals of Noise and Vibration Analysis for Engineers; Cambridge University Press: Cambridge, UK, 2003; ISBN 9780521499132. [Google Scholar]
- Nasser, A.; Mansour, A.; Yao, K.C.; Abdallah, H.; Charara, H. Spectrum sensing based on cumulative power spectral density. EURASIP J. Adv. Signal Process. 2017, 2017, 38. [Google Scholar] [CrossRef] [Green Version]
- Aderikhin, V.I.; Burenkov, Y.A.; Sargsyan, M.V.; Uzdin, R.I. Improvement of the national primary standard for the unit of radio-frequency noise spectral power density. Meas. Tech. 2013, 55, 1335–1343. [Google Scholar] [CrossRef]
- Yakimov, V.N. Direct spectral power density estimation from a discrete-time representation of stochastic analog quantization for an analog random process. Meas. Tech. 2009, 52, 223–230. [Google Scholar] [CrossRef]
- Xu, C.; Tian, H.; Reece, C.E.; Kelley, M.J. Enhanced characterization of niobium surface topography. Phys. Rev. Spec. Top.-Accel. Beams 2011, 14, 123501. [Google Scholar] [CrossRef] [Green Version]
- Mwema, F.M.; Akinlabi, E.T.; Oladijo, O.P.; Oladijo, O.P. The Use of Power Spectrum Density for Surface Characterization of Thin Films. In Photoenergy and Thin Film Materials; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2019; pp. 379–411. [Google Scholar]
- Youngworth, R.N.; Gallagher, B.B.; Stamper, B.L. An overview of power spectral density (PSD) calculations. In Optical Manufacturing and Testing VI; Stahl, H.P., Ed.; International Society for Optics and Photonics: Bellingham, WA, USA, 2005; p. 58690U. [Google Scholar]
- Jacobs, T.D.B.; Junge, T.; Pastewka, L. Quantitative characterization of surface topography using spectral analysis. Surf. Topogr. Metrol. Prop. 2017, 5, 013001. [Google Scholar] [CrossRef]
- Elson, J.M.; Bennett, J.M. Calculation of the power spectral density from surface profile data. Appl. Opt. 1995, 34, 201. [Google Scholar] [CrossRef]
- Cutler, C.; Lee, C.-B.; Thackeray, J.W.; Mack, C.; Nelson, J.; DeSisto, J.; Li, M.; Aqad, E.; Hou, X.; Marangoni, T.; et al. Utilizing Roughness Power Spectral Density Variables to Guide Resist Formulation and Understand Impact of Frequency Analysis through Process. J. Photopolym. Sci. Technol. 2018, 31, 679–687. [Google Scholar] [CrossRef] [Green Version]
- Duparré, A.; Ferre-Borrull, J.; Gliech, S.; Notni, G.; Steinert, J.; Bennett, J.M. Surface characterization techniques for determining the root-mean-square roughness and power spectral densities of optical components. Appl. Opt. 2002, 41, 154. [Google Scholar] [CrossRef] [Green Version]
- Gwyddion—Free SPM (AFM, SNOM/NSOM, STM, MFM, …) Data Analysis Software. Available online: http://gwyddion.net/ (accessed on 10 December 2021).
- Gong, Y.; Misture, S.T.; Gao, P.; Mellott, N.P. Surface Roughness Measurements Using Power Spectrum Density Analysis with Enhanced Spatial Correlation Length. J. Phys. Chem. C 2016, 120, 22358–22364. [Google Scholar] [CrossRef]
- Ferré-Borrull, J.; Duparré, A.; Quesnel, E. Procedure to characterize microroughness of optical thin films: Application to ion-beam-sputtered vacuum-ultraviolet coatings. Appl. Opt. 2001, 40, 2190. [Google Scholar] [CrossRef]
- Caro, J.; Doudkowsky, M.; Figueras, A.; Fraxedas, J.; García, G.; Santiso, J.; Schamm, S.; Ojeda, F.; Vázquez, L.; Albella, J.M.; et al. Morphological and Structural Aspects of Thin Films Prepared by Vapor Deposition. In Handbook of Surfaces and Interfaces of Materials; Academic Press: Cambridge, MA, USA, 2001. [Google Scholar]
- Cutler, C.; Thackeray, J.W.; Trefonas, P.; Millward, D.; Lee, C.-B.; Mack, C. Pattern roughness analysis using power spectral density: Application and impact in photoresist formulation. J. Micro/Nanopatterning Mater. Metrol. 2021, 20, 010901. [Google Scholar] [CrossRef]
- Mack, C.A. Reaction-diffusion power spectral density. J. Micro/Nanolithography MEMS MOEMS 2012, 11, 043007. [Google Scholar] [CrossRef]
- Kneipp, K.; Kneipp, H.; Itzkan, I.; Dasari, R.R.; Feld, M.S. Surface-enhanced Raman scattering and biophysics. J. Phys. Condens. Matter 2002, 14, 202. [Google Scholar] [CrossRef] [Green Version]
- Xu, H.; Wang, X.H.; Persson, M.P.; Xu, H.Q.; Käll, M.; Johansson, P. Unified treatment of fluorescence and Raman scattering processes near metal surfaces. Phys. Rev. Lett. 2004, 93, 243002. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Berneschi, S.; Righini, G.C.; Pelli, S. Towards a Glass New World: The Role of Ion-Exchange in Modern Technology. Appl. Sci. 2021, 11, 4610. [Google Scholar] [CrossRef]
- Zhurikhina, V.V.; Petrov, M.I.; Sokolov, K.S.; Shustova, O.V. Ion-exchange characteristics of sodium-calcium-silicate glass: Calculation from mode spectra. Tech. Phys. 2010, 55, 1447–1452. [Google Scholar] [CrossRef]
- Redkov, A.V.; Zhurikhina, V.V.; Lipovskii, A.A. Formation and self-arrangement of silver nanoparticles in glass via annealing in hydrogen: The model. J. Non-Cryst. Solids 2013, 376, 152–157. [Google Scholar] [CrossRef]
- Blackie, E.J.; Le Ru, E.C.; Etchegoin, P.G. Single-molecule surface-enhanced raman spectroscopy of nonresonant molecules. J. Am. Chem. Soc. 2009, 131, 14466–14472. [Google Scholar] [CrossRef] [PubMed]
- Weroński, P. Roughness of surface decorated with randomly distributed pillars. Sci. Rep. 2018, 8, 16045. [Google Scholar] [CrossRef] [PubMed]
- Chen, T.; Pal, A.; Gao, J.; Han, Y.; Chen, H.; Sukhishvili, S.; Du, H.; Podkolzin, S.G. Identification of Vertical and Horizontal Configurations for BPE Adsorption on Silver Surfaces. J. Phys. Chem. C 2015, 119, 24475–24488. [Google Scholar] [CrossRef]






Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Babich, E.; Scherbak, S.; Lubyankina, E.; Zhurikhina, V.; Lipovskii, A. Power Spectral Density Analysis for Optimizing SERS Structures. Sensors 2022, 22, 593. https://doi.org/10.3390/s22020593
Babich E, Scherbak S, Lubyankina E, Zhurikhina V, Lipovskii A. Power Spectral Density Analysis for Optimizing SERS Structures. Sensors. 2022; 22(2):593. https://doi.org/10.3390/s22020593
Chicago/Turabian StyleBabich, Ekaterina, Sergey Scherbak, Ekaterina Lubyankina, Valentina Zhurikhina, and Andrey Lipovskii. 2022. "Power Spectral Density Analysis for Optimizing SERS Structures" Sensors 22, no. 2: 593. https://doi.org/10.3390/s22020593
APA StyleBabich, E., Scherbak, S., Lubyankina, E., Zhurikhina, V., & Lipovskii, A. (2022). Power Spectral Density Analysis for Optimizing SERS Structures. Sensors, 22(2), 593. https://doi.org/10.3390/s22020593