A Back-EMF Estimation Error Compensation Method for Accurate Rotor Position Estimation of Surface Mounted Permanent Magnet Synchronous Motors
Abstract
:1. Introduction
2. System Modeling
2.1. Back-EMF-Based Sensorless Method [4,5]
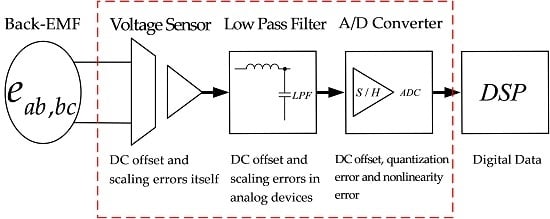
2.2. Effect of DC Offset Error
3. The Proposed DC Offset Error Compensation Method
4. Simulation
5. Experimental Results
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A

References
- Baik, I.C. Improved nonlinear speed control of PM synchronous motor using time delay control. J. Power Electron. 2003, 3, 197–204. [Google Scholar]
- Murakami, H.; Honda, Y.; Kiriyama, H.; Morimoto, S.; Takeda, Y. The performance comparison of SPMSM, IPMSM, and SynRM in use as air-conditioning compressor. In Proceedings of the Conference Record of the 1999 IEEE Industry Applications Conference: Thirty-Fourth IAS Annual Meeting, Phoenix, AZ, USA, 3–7 October 1999; Volume 2, pp. 840–845. [Google Scholar]
- Bae, B.H.; Sul, S.K.; Kwon, J.H.; Byeon, J.S. Implementation of sensorless vector control for super-high-speed PMSM of turbo-compressor. IEEE Trans. Ind. Appl. 2003, 39, 811–818. [Google Scholar] [CrossRef]
- Lee, K.W.; Ha, J.I. Evaluation of back-EMF estimators for sensorless control of permanent magnet synchronous motors. J. Power Electron. 2012, 12, 604–614. [Google Scholar] [CrossRef]
- Lee, Y.; Kwon, Y.; Sul, S. Comparison of rotor position estimation performance in fundamental-model-based sensorless control of PMSM. In Proceedings of the 2015 IEEE Energy Conversion Congress and Exposition (ECCE), Montreal, QC, Canada, 20–24 September 2015; Volume 7, pp. 5624–5633. [Google Scholar]
- Mizutani, R.; Takeshita, T.; Matsui, N. Current model-based sensorless drives of salient-pole PMSM at low speed and standstill. IEEE Trans. Ind. Appl. 1998, 34, 841–846. [Google Scholar] [CrossRef]
- Matsui, N. Sensorless PM Brushless DC motor drives. IEEE Trans. Ind. Electron. 1996, 43, 300–308. [Google Scholar] [CrossRef]
- Chen, Z.; Tomita, M.; Ichikawa, S.; Okuma, S. Sensorless control of interior permanent magnet synchronous motor by estimation of an extended electromotive force. In Proceedings of the Conference Record of the 2000 IEEE Industry Applications Conference, Rome, Italy, 8–12 October 2000; Volume 3, pp. 1814–1819. [Google Scholar]
- Ogasawara, S.; Akagi, H. Implementation and position control performance of a position-sensorless IPM motor drive system based on magnetic saliency. IEEE Trans. Ind. Appl. 1998, 34, 806–812. [Google Scholar] [CrossRef] [Green Version]
- Kim, S.M.; Ha, J.I.; Sul, S.K. PWM switching frequency signal injection sensorless method in IPMSM. IEEE Trans. Ind. Appl. 2012, 48, 1576–1587. [Google Scholar] [CrossRef]
- Ciobotaru, M.; Teodorescu, R.; Agelidis, V.G. Offset rejection for PLL based synchronization in grid-connected converters. In Proceedings of the Twenty-Third Annual IEEE Applied Power Electronics Conference and Exposition, Austin, TX, USA, 24–28 February 2008; pp. 1611–1617. [Google Scholar]
- Karimi-Ghartemani, M.; Khajehoddin, S.A.; Jain, P.K.; Bakhshai, A.; Mojiri, M. Addressing DC component in PLL and notch filter algorithms. IEEE Trans. Power Electron. 2012, 27, 78–86. [Google Scholar] [CrossRef]
- Park, C.S.; Jung, T.U. Improved DC offset error compensation algorithm in phase locked loop system. JEET 2016, 11, 1707–1713. [Google Scholar] [CrossRef]
- Hwang, S.H.; Liu, L.; Kim, J.M. DC offset error compensation for synchronous reference frame PLL in single-phase grid-connected converters. IEEE Trans. Power Electron. 2012, 27, 3467–3471. [Google Scholar] [CrossRef]
- Chung, D.W.; Sul, S.K. Analysis and compensation of current measurement error in vector-controlled AC motor drives. IEEE Trans. Ind. Appl. 1998, 34, 340–345. [Google Scholar] [CrossRef]
- Qian, W.; Panda, S.K.; Xu, J.X. Torque ripple minimization in PM synchronous motors using iterative learning control. IEEE Trans. Power Electron. 2004, 19, 272–279. [Google Scholar] [CrossRef]
- Jung, H.S.; Hwang, S.H.; Kim, J.M.; Kim, C.U.; Choi, C. Diminution of current measurement error for vector-controlled AC motor drives. IEEE Trans. Ind. Appl. 2006, 42, 1249–1256. [Google Scholar] [CrossRef]
- Cho, K.R.; Seok, J.K. Correction on current measurement errors for accurate flux estimation of AC drives at low stator frequency. IEEE Trans. Ind. Appl. 2008, 44, 594–603. [Google Scholar] [CrossRef]
- Lu, H.; Jiang, M.; Guo, X.; Chen, Q. Sensorless position control of SPMLSM based on high-gain observer. J. Comput. 2013, 3, 661–668. [Google Scholar] [CrossRef]
- Su, Y.X.; Zheng, C.H.; Duan, B.H. Automatic disturbances rejection controller for precise motion-control of permanent-magnet synchronous motors. IEEE Trans. Ind. Electron. 2005, 3, 814–823. [Google Scholar] [CrossRef]



















| Quantity | Symbol | Value |
|---|---|---|
| Rated voltage | V | 30 V |
| Rated current | I | 1.4 A |
| Rated speed | 3000 r/min | |
| Maximum speed | 3500 r/min | |
| Stator resistance | 0.9 Ω | |
| Stator inductance | L | 1.35 mH |
| Number of pole | P | 4 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jung, T.-U.; Jang, J.-H.; Park, C.-S. A Back-EMF Estimation Error Compensation Method for Accurate Rotor Position Estimation of Surface Mounted Permanent Magnet Synchronous Motors. Energies 2017, 10, 1160. https://doi.org/10.3390/en10081160
Jung T-U, Jang J-H, Park C-S. A Back-EMF Estimation Error Compensation Method for Accurate Rotor Position Estimation of Surface Mounted Permanent Magnet Synchronous Motors. Energies. 2017; 10(8):1160. https://doi.org/10.3390/en10081160
Chicago/Turabian StyleJung, Tae-Uk, Jung-Hoon Jang, and Chang-Seok Park. 2017. "A Back-EMF Estimation Error Compensation Method for Accurate Rotor Position Estimation of Surface Mounted Permanent Magnet Synchronous Motors" Energies 10, no. 8: 1160. https://doi.org/10.3390/en10081160
APA StyleJung, T. -U., Jang, J. -H., & Park, C. -S. (2017). A Back-EMF Estimation Error Compensation Method for Accurate Rotor Position Estimation of Surface Mounted Permanent Magnet Synchronous Motors. Energies, 10(8), 1160. https://doi.org/10.3390/en10081160