Fundamental Evaluation of Thermal Switch Based on Ionic Wind
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Methods
2.2. Numerical Simulation
3. Results and Discussion
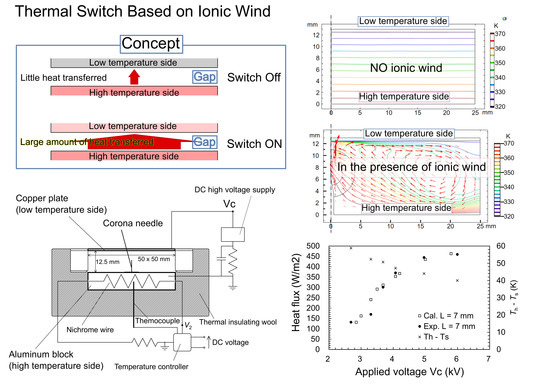
3.1. The Heat Transfer by Natural Convection and Analysis of the Rate of Heat Flow (Q)
3.2. The Effect of Ionic Wind
3.2.1. The Corona Onset Voltages (Vo)
3.2.2. The Relationship Between Applied Voltage and the Rate of Heat Transfer
3.2.3. Energy Efficiencies
3.2.4. The Influence of the Heat Generation by Corona Discharge in the Gap
4. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Kato, Y.; Suzuki, H.; Shikazono, N. Heat storage, transportation, and transfer. In Energy Technology Roadmaps of Japan: Future Energy Systems Based on Feasible Technologies Beyond 2030; Kato, Y., Koyama, M., Eds.; Springer: Cham, Switzerland, 2016; pp. 135–146. [Google Scholar]
- Key World Energy Statics; International Energy Agency: Paris, France, 2018; Available online: https://www.iea.org/ (accessed on 1 June 2019).
- Gou, X.; Ping, H.; Ou, Q.; Xiao, H.; Qing, S. A novel thermoelectric generation system with thermal switch. Appl. Energy 2015, 160, 843–852. [Google Scholar] [CrossRef]
- Gu, W.; Tang, G.-H.; Tao, W.-Q. Thermal switch and thermal rectification enabled by near-field radiative heat transfer between three slabs. Int. J. Heat Mass Transf. 2015, 82, 429–434. [Google Scholar] [CrossRef]
- Velson, N.V.; Tarau, C.; Anderson, W.G. Two-Phase Thermal Switch for Spacecraft Passive Thermal Management. In Proceedings of the 45th International Conference on Environmental Systems, Bellevue, WA, USA, 12–16 July 2015. [Google Scholar]
- Cha, G.; Kim, C.-J.; Ju, Y.S. Thermal conductance switching based on the actuation of liquid droplets through the electrowetting on dielectric (EWOD) phenomenon. Appl. Therm. Eng. 2016, 98, 189–195. [Google Scholar] [CrossRef] [Green Version]
- Gong, J.; Cha, G.; Ju, Y.S.; Kim, C.-J. Thermal Switches Based on Coplanar EWOD for Satellite Thermal Control. In Proceedings of the 2008 IEEE 21st International Conference on Micro Electro Mechanical Systems (MEMS), Wuhan, China, 13–17 January 2008. [Google Scholar]
- McLanahan, A.L.R.; Richards, C.D.; Richards, R.F. A Dielectric Liquid Contact Thermal Switch with Electrowetting Actuation. In Proceedings of the ASME 2010 International Mechanical Engineering Congress & Exposition IMECE2010, Vancouver, BC, Canada, 12–18 November 2010; pp. 61–66. [Google Scholar]
- Tasaki, Y. Present status and approach to a room-temperature magnetic refrigerator with thermal switches. J. Cryog. Supercond. Soc. Jpn. 2015, 50, 53–59. [Google Scholar] [CrossRef]
- Velkoff, H.R.; Godfrey, R. Low-velocity heat transfer to a flat plate in the presence of a corona discharge in air. J. Heat Transf. 1979, 101, 157–163. [Google Scholar] [CrossRef]
- Franke, M.E.; Hutson, K.E. Effect of corona discharge on free-convection heat transfer inside a vertical hollow cylinder. J. Heat Transf. 1984, 106, 347–351. [Google Scholar] [CrossRef]
- Tada, Y.; Takimoto, A.; Hayashi, Y. Heat transfer enhancement in a corona field by applying ionic wind. Enhanc. Heat Transf. 1997, 4, 71–86. [Google Scholar] [CrossRef]
- Kawamoto, H.; Umezu, S. Electrostatic micro-ozone fan that utilizes ionic wind induced in pin-to-plate corona discharge system. J. Electrostat. 2008, 66, 445–454. [Google Scholar] [CrossRef]
- Zhang, J.; Lai, F.C. Heat transfer enhancement using corona wind generator. J. Electrostat. 2018, 92, 6–13. [Google Scholar] [CrossRef]
- Tsui, Y.-Y.; Huang, Y.-X.; Lan, C.-C.; Wang, C.-C. A study of heat transfer enhancement via corona discharge by using a plate corona electrode. J. Electrostat. 2017, 87, 1–10. [Google Scholar] [CrossRef]
- Deylami, H.M.; Amanifard, N.; Dolati, F.; Kouhikamali, R.; Mostajiri, K. Numerical investigation of using various electrode arrangements for amplifying the EHD enhanced heat transfer in a smooth channel. J. Electrostat. 2013, 71, 656–665. [Google Scholar] [CrossRef]
- Mahmoudi, A.R.; Pourfayaz, F.; Kasaeian, A. A simplified model for esitmating heat transfer coefficient in a chamber with electohydrodynamic effect (corona wind). J. Electrostat. 2018, 93, 125–136. [Google Scholar] [CrossRef]
- Lakeh, R.B.; Molki, M. Enhancement of convective heat transfer by electrically-induced swirling effect in laminar and fully-developed internal flows. J. Electrostat. 2013, 71, 1086–1099. [Google Scholar] [CrossRef]
- Lakeh, R.B.; Molki, M. Targeted heat transfer augmentation in circular tubes using a corona jet. J. Electrostat. 2012, 70, 31–42. [Google Scholar] [CrossRef]
- Takahashi, K. The Foundation of Aerosol Science; Morikita Publishing Co., Ltd.: Tokyo, Japan, 2003. [Google Scholar]
- Chen, J.; Davidson, J.H. Model of the negative dc corona plasma: Comparison to the positive dc corona plasma. Plasma Chem. Plasma Process. 2003, 23, 83–102. [Google Scholar] [CrossRef]
- Farnoosh, N.; Adamiak, K.; Castle, G.S.P. 3-D numerical analysis of EHD turbulent flow and mono-disperse charge particle transport and collection in a wire-plate EHD. J. Electrostat. 2010, 68, 513–522. [Google Scholar] [CrossRef]
- Kanamoto, H.; Yasuda, H.; Umezu, S. Flow distribution and pressure of air due to ionic wind in pin-to-plate corona discharge system. J. Electrostat. 2006, 64, 400–407. [Google Scholar] [CrossRef]
- Tokyo Japan Society of Mechanical Engineers. JSME Data Book: Heat Transfer, 3rd ed.; Japan Society of Mechanical Engineers: Tokyo, Japan, 1976. [Google Scholar]
- Cobine, J.D. Gaseous Conductors: Theory and Engineering Applications; Dover Publications Inc.: New York, NY, USA, 1957; p. 606. [Google Scholar]














| L (mm) | Vo (kV) |
|---|---|
| 6.0 | 3.46 |
| 7.0 | 2.85 |
| 8.0 | 2.65 |
| 9.0 | 2.38 |
| Vc (kV) | K (W/(K·m2)) | Kon/Koff | ||
|---|---|---|---|---|
| Experiment | Calculation | Experiment | Calculation | |
| L = 6 mm | ||||
| 0 | 2.32 | 2.31 | - | - |
| 3.5 | 2.32 | 3.25 | 1 | 1.41 |
| 4.1 | 5.36 | 5.77 | 2.31 | 2.50 |
| 4.5 | 6.58 | 6.88 | 2.84 | 2.98 |
| 5.0 | 7.16 | 8.41 | 3.08 | 3.64 |
| L = 7 mm | ||||
| 0 | 2.32 | 2.31 | - | - |
| 3.3 | 3.24 | 4.60 | 1.45 | 2.06 |
| 3.7 | 5.94 | 6.14 | 2.65 | 2.75 |
| 4.1 | 7.85 | 7.49 | 3.50 | 3.35 |
| 5.0 | 10.1 | 9.90 | 4.50 | 4.43 |
| 6.0 | 11.5 | 11.7 | 5.12 | 5.25 |
| L = 8 mm | ||||
| 0 | 2.32 | 2.31 | - | - |
| 2.7 | 2.32 | 4.01 | 1.0 | 1.78 |
| 3.1 | 4.38 | 5.32 | 1.93 | 2.36 |
| 3.6 | 5.26 | 6.30 | 2.32 | 2.79 |
| 4.0 | 6.39 | 7.62 | 2.82 | 3.37 |
| 4.5 | 7.74 | 9.02 | 3.41 | 4.00 |
| L = 9 mm | ||||
| 0 | 2.32 | 2.31 | - | - |
| 2.8 | 2.33 | 4.11 | 1.01 | 1.79 |
| 3.1 | 3.59 | 5.42 | 1.55 | 2.36 |
| 3.5 | 5.23 | 6.06 | 2.26 | 2.63 |
| 4.1 | 6.79 | 8.06 | 2.93 | 3.50 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yoshida, K. Fundamental Evaluation of Thermal Switch Based on Ionic Wind. Energies 2019, 12, 2963. https://doi.org/10.3390/en12152963
Yoshida K. Fundamental Evaluation of Thermal Switch Based on Ionic Wind. Energies. 2019; 12(15):2963. https://doi.org/10.3390/en12152963
Chicago/Turabian StyleYoshida, Keiichiro. 2019. "Fundamental Evaluation of Thermal Switch Based on Ionic Wind" Energies 12, no. 15: 2963. https://doi.org/10.3390/en12152963
APA StyleYoshida, K. (2019). Fundamental Evaluation of Thermal Switch Based on Ionic Wind. Energies, 12(15), 2963. https://doi.org/10.3390/en12152963