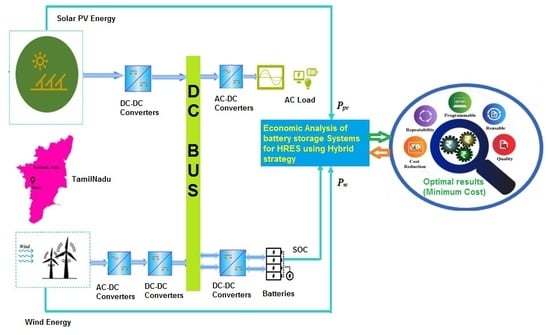
In this section, the economic analysis of the HRES system without and with energy storage is considered. The proposed technique is implemented in the MATLAB/Simulink platform. In order to meet the load demand of the system, PV, WT and battery have been utilized. HOMER is a free software application developed by the National Renewable Energy Laboratory in the United States. This software application is used to design and evaluate technically and financially the options for the off-grid and on-grid power systems for remote, stand-alone and distributed generation applications. It allows considering a large number of technological options to account for energy resource availability and other variables.
Case Study A: Cost worked out for the interruption period without using energy storage.
Case Study B: Cost worked out using proposed technique for the interruption period with energy storage.
7.1. Case Study A
The existing 22 kV Vagarai feeder consists of one standalone 1.5 MW wind turbine (
W1), one 1.5 MW wind turbine (
W2-
PV) combined in a hybrid system with a 0.300 MW solar PV system and one standalone 2.8 MW wind turbine (
W3). In this case, study A, the cost analysis for the interruption period without using energy storage has been analyzed. Here, there is no generation during load curtailment and interruption periods of the system due to non-availability of battery storage. The results of case study A mainly show the impacts of higher load curtailment i.e., fault trip, main supply failure, shutdowns, etc.
Table 1 lists the amount of energy really sold to the TANTRANSCO grid in KWHr and the actual cost of the electricity (
$/month).
The quantum of the energy really purchased from the TANTRANSCO grid in KWHr and the actual cost paid for the electricity (
$/month) is derived in
Table 2. The MATLAB/Simulation proves the generation cost is optimum after consideringthe sale of excess stored power. The total price (
$/month) of electricity sold to grid monthly is denoted as
IImport−month.
The export of energy from the wind turbine (
W1) is denoted as
EW1, the export of energy from wind turbine (
W2) plus solar Photo Voltaic (
PV) is denoted as (
EW2-PV) and the export of energy from the wind turbine (
W3) is denoted as
EW3 (per unit of power purchased from TANTRANSCO in INR is 3.30 [
$ 0.48] for the
W1 and
W2 plus PV solar hybrid system and INR 3.70 for
W3 [1 INR =
$0.015].
CW1 is the cost of the sale of power to grid due to the standalone 1.5 MW wind turbine.
CW2 is the cost of the sale of power to the grid due to the hybrid 1.5 MW wind turbine combined with the 0.300 MW solar PV systems and
CW3 is the cost of the sale of power to the grid due to the standalone 2.8 MW wind turbine. The import of energy from the wind turbine (
W1) is denoted as
IW1, The export of energy from the wind turbine (
W2) plus solar PV systemis denoted as
IW2 PV and the export of energy from the wind turbine (
W3) is denoted as
IW3 and per unit of power purchased from TANTRANSCO in INR is 3.30 [
$0.48] for
W1 and
W2 plus solar PV hybrid system; and INR 3.70 is for
W3 [1 INR =
$0.015]. Similarly, the import of energy for the wind turbine (
W1) is denote as
IW1, the import of energy for the wind turbine (
W2) plus solar PV systemis denoted as
IW2 PV and the import of energy for the wind turbine (
W3) is denoted as
IW3. Here, the export of energy from wind turbine (
W1) is denoted as
EW1 in column (2); export of energy from wind turbine (
W2) plus solar PV is denoted as
EW2 PV in column (3); and export of energy from wind turbine (
W3) is denoted as E
W3.The amountof energy really purchased by the grid through 22 kV feeders in the 110/22 kV Vagarai SS is tabulated in
Table 2.
The actual current flown at 01.00 hon 19 July 2018 in all segments like 22 kV side, LV 1, LV2, Bus 1 and Bus 2; 110 kV side, GC and 110 kV Udumalpet/Renganathapuram in the switch yard is shown in
Figure 7.
The hourly readings of the five 22 kV feeders in the 110/22 kV Vagarai substation and the L.V 1 and L.V 2 of the power transformers1 and 2 on 19 July 2018 are tabulated in
Table 3 and
Table 4.
The 22 kV Bus 2 is connected with three 22 kV feeders, namely (1) Hybrid Generation Regen feeder, (2) Agen Vijay feeder and (3) Appanuthu feeder; whereas the 22 kV Bus 1 is connected with two 22 kV feeders, namely (4) VepanValasu feeder and (5) Mill feeder in the 110/22 kV Vagarai substation.
From
Figure 7 and
Table 3, it is seen that the required load was only 60 Amps (30 Amps each for the 22 kV Appanuthu and Agen Vijay feeders) on 22 kV Bus 2 and 75 Amps (10 Amps for 22 kV Mill feeder and 65 Amps for the 22 kV VepanValasu feeder).As the Bus coupler switch No. 12 was kept in an open condition, at 01.00 hon 19 July 2018, the power for an amount of 2.57 MW (75 Amps) out of 5.5 MW (160 Amps) from the hybrid feeder was stepped up to 110 kV by the power transformer (Pr. Tr)-2. And stepped down to 22 kV voltage level by power transformer (Pr. Tr)-1, (or, say from LV-2-Pr.Tr.2–Pr.Tr.1-LV-1) from the balance power of the 22 kV regen feeder, which is kept at 22 kV Bus-2.
Anamount of current of 100 Amps at the 22 kV side got transformed through the power transformer, as 20 Amps at the 110 kV side; and only an amount of 15 Amps at 110 kV equivalent to 5 Amps for the 22 kV side required for Bus 1. The balance amountof 5 Amps would flow to the 110 kV GC and finally be exported through 110 kV Udumalpet/Ranganathapuram feeders. Or, one can say that the required load demand for the 22 kV Veppen Valasu and 22 kV turbinefeeders was only 75 Amps @ 01.00 h, and the balance 25 Amps was fed into the power transformer 1 and stepped up to110 kV.
The actual current flown on all the 22 kV feeders in the 22 kV side in both the 22 kV Bus 1 and Bus 2 are given in
Table 4 and
Figure 7. At 01.00 h, the demand of the 22 kV Agen Vijay and Appanuthu feeders was 30 Amps each, whereas the hybrid generation of the regen feeder was 160 Amps.
Similarly, duringeach hour of 19 July 2018, the actual incoming generation from the hybrid regen feeder and the load demand of the remainingfour22 kV feeders and power flow to/from the 110 kV GC are recorded and charted in
Table 3.
The time vs. current (in Amps) graph is given in
Figure 8. From the graph, it is understood that the wind generation alone on the 22 kV hybrid feeder balanced the entire load of four 22 kV feeders. The unutilized amount of energy had been exported through the 110 kV Udumalpet/Ranganathapuram feeders from 01.00 a.m. to 06.00 a.m. on 19 July 2018.
As the load increased during the day hours and as the hybrid generation could not cater to the load, 110 kV GC imported power through the 110 kV Udumalpet/Ranganathapuram feeders from 7.00 a.m. onwards. If the 22 kV regen feeder is kept connected only with the solar generation, then there would not be any green energy from the wind and it would not fulfil the requirement at least up to some early hours of the day. In addition, if an energy storage system were implemented in the HRES, it would be more economical and beneficial and facilitate the generation of green energy even during predictable interruptions and curtailment periods also using the interconnectivity of the same grid.
The following
Table 5 is a summary of various interruptions occurred in the 110 kV Vagarai SS during the year of 2018.
From the table, it is understood that seven various types of generation interruption have occurredfor a total of 212 hours and 27 min during the year 2018. The different types of interruptions are described as fault trip, (b) load shedding, (c) hand trip, (d) main 110 kV supply failure, (e) total shut down (f) line clear and (g) breakdown of other feeders and equipment.Asummary of all month wiseinterruptions during the year of 2018 in the 110/22 kV Vagarai SS is presented in
Table 6. All the interruptions can be grouped into two segments, some interruptions were predictable, and others were not predictable.
7.1.1. Interruptions That Would Not Be Predictable and Can Occur Suddenly
Interruptions like (a) fault trip, (b) load shedding (c) hand trip and (d) main 110 kV supply failure are categorized in this group. These interruptions could not be predicted. However, if a proper energy storage system is available; the energy can be stored by diverting the output through the breaker to the energy storage system. The number of occurrences of said unpredictable interruptions was 93 in the year 2018 but the total duration of the interruptions is only 27 h and 57 min, as given in
Table 7.
7.1.2. Interruptions That Are Predictable and Carried Out with Prior Intimation
Interruptions like (e) total shut down, (f) line clear and (g) proposed break down (BD) of other feeders and equipment are categorized in this group. The occurrence of the predictable interruptions during the year 2018, in the 110/22 kV Vagarai SS was 24 in number, but the duration was 184 h 30 min, as tabulated in
Table 8.
These interruptions are normally taken intentionally for maintenance of equipment in the yard of the substation, it can be predictable, and in fact, the details of the interruptions would be conveyed over phone before being carried out. The duration of the interruptions isvery largeand the green power from the renewable energy sources can be stored; if a proper energy system is incorporated. As there is an alternative supply available for running the wind turbines, it can be possible to harness the green energy and store it in the energy storage system to be sold to the grid in the future.
7.2. Case Study B
In the case study B, the cost analysis for the interruption period using the proposed technique with energy storage has been analyzed. Here, the loss of the production of the green energy during grid interruptions and wind curtailment of the system are minimized because of the presence of battery storage using the proposed technique. Consequently, the proposed system gives lower cost with an optimal solution. The power flow in the HRES system using battery storage is analyzed forone day and one year. The variation of load per day and for a year is depicted in
Figure 9.
Figure 9a the depicts how with the proposed technique the load demand is calculated during the time period of 24 h and
Figure 9b illustrates the monthly load demand of the proposed technique. From
Figure 9a, it is observed that the maximum hourly load demand of 5.9 MW is reached in the time intervals of 5 to 10 h. Likewise from
Figure 9b, the maximum monthly load demand 1.39 × 10
4 KW is reached during the time period of 10 to 12 h.
The graphs of irradiance and wind speed for a 24 h. period are plotted in
Figure 10. From
Figure 10a, it is observed that the irradiance of the system is a maximum of 1000 W/m
2 during the time-period of 10 to 15 h. The maximum wind speed 12 m/s is predicted at the time moment of 5 to 15 h. in
Figure 10b.
Figure 11 shows the comparison analysis of power generated using energy storage, HOMER and the proposed technique for one day.
Figure 11a depicts the graph of power versus time using the energy storage system. It is observed from
Figure 11a, that by using the energy storage the maximum power 0.049 MW is generated in a period of 2 to 7 h.
Figure 11b depicts the power generated using HOMER. By utilizing HOMER, the maximum power 0.047 MW is produced during the time interval of 20 to 25 h.
Figure 11c shows the power generated using proposed technique. The maximum power generated using proposed technique is 0.05 MW at the time duration of 3 to 5 h.
Figure 12 shows the comparison analysis of power generated using energy storage, HOMER and proposed technique for one year.
Figure 12a depicts agraph of power versus time using energy storage system. It is observed from the
Figure 12a, which by using the energy storage the maximum power 1 MW is generated at the time period of 2 to 7 h.
Figure 12b depicts the power generated using HOMER. By utilizing HOMER, the maximum power 1.3 MW is produced during the time interval of 2 to 4 h.
Figure 13 shows the individual generated power analysis using ESS, Without ESS, HOMER and Proposed for one day.
Figure 13a shows the individual generated power using ESS.
Figure 13a analyzes the PV, WT1, WT2 and WT3 generated power during the time period of 24 h. As seen from
Figure 13a, the power generated by PV, WT1, WT2 and WT3 reaches the peak of 5.7 MW during the time instant of 5 to 10 h.
Figure 13b shows the individual generated power without considering the ESS. From
Figure 13b, it is observed that the power generated is in the maximum range of 5.75 MW at the time interval of 5 to 10 h.
Figure 13c explains the individual generated power using HOMER. It is observed from the figure that the power generation is maximum 5.8 MW at the time duration of 5 to 10 h.
Figure 13d delineates the individual generated power using the proposed technique. From
Figure 13d, it is seen that the maximum power 5.9 MW is generated during the time interval of 5 to 10 h.
Figure 14 shows the individual generated power analysis using ESS, without ESS, HOMER and the proposed technique for one year.
Figure 14a shows the individual generated power using ESS.
Figure 14a analyzes the PV, WT1, WT2 and WT3 generated power during the time period of 24 h. As seen from
Figure 14a, the power generated by PV, WT1, WT2 and WT3 reaches a peak of 160 MW during the time period of 6 to 8 h.
Figure 14b shows the individual generated power without considering the BESS. From
Figure 14b, it is observed that the power generated is in the maximum range of 155 MW during the time interval of 6 to 8 h.
Figure 14c explains the individual generated power using HOMER. It is observed from the figure that the power generation is maximum 160 at the time periodof 6 to 8 h.
Figure 14d delineates the individual generated power using proposed technique. From the
Figure 14d, the maximum power 170 MW is generated during the time interval from 6 to 8 h.
Figure 15 shows the investigation of fitness graph for one day. It depicts the fitness comparison for one day. As seen from the figure, the base method solution converges after an iteration count of 32. The HOMER fitness solution converges at the 38
th iteration and the proposed technique gives the solution faster than the other techniques.
Figure 16 shows the investigation of cost for one day and one year.
Figure 16a depicts the graph of cost versus time. The cost of the proposed technique is more optimal for one day than the other techniques such as without ESS, Base and HOMER.
Figure 16b depicts the graph of cost versus time. The cost of the proposed technique is more optimal for one year than the other techniques such as without ESS, Base and HOMER.
Figure 17 shows the investigation of fitness graph for one year.
As seen from the
Figure 17, the base method solution converges after 49 iterations. The HOMER fitness solution converges at the 41
st iteration and the proposed technique gives the solution faster than the other techniques.