Analysis of Coupled Wellbore Temperature and Pressure Calculation Model and Influence Factors under Multi-Pressure System in Deep-Water Drilling
Abstract
:1. Introduction
2. Mathematical Model of Each Heat Transfer Region
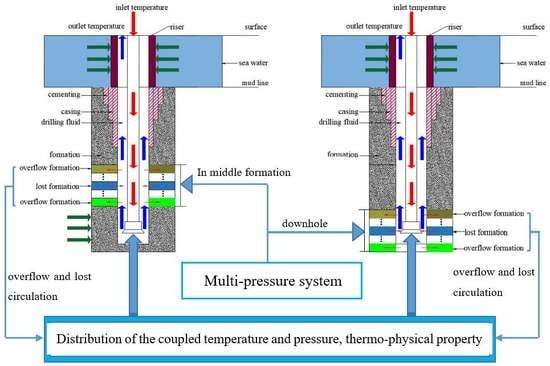
2.1. Physical Model of All Heat Transfer Regions
2.2. Mathematical Model
2.2.1. Model Hypothesis
- (1)
- All fluids in the model are incompressible, other thermo-physical parameters do not change with temperature and pressure variation except viscosity and density.
- (2)
- Radial gradient of the temperature, pressure, and flow rate inside the wellbore are neglected and the radial heat conduction inside seawater and formation is considered.
- (3)
- The layer of overflow and the leakage alternate with each other; the flow rate of the same type of sublayer is the same, and the fluid entering the annulus is evenly mixed with the drilling fluid.
2.2.2. Heat Transfer Mathematic Models for Each Region
2.2.3. Momentum Equation and the Relationship between Pressure and Density
2.3. Initial and Boundary Conditions
2.3.1. Initial Conditions
2.3.2. Boundary Conditions
3. Model Validation
3.1. Comparison and Verification with Theoretical Calculation Model
3.2. Verification by Comparison with Measured Data
4. Analysis of Key Factors Influencing Wellbore Temperature Distribution
4.1. Annulus Temperature Distribution When Overflow and Leakage Rates Are Different under the Multi-Pressure System
4.2. Annulus Temperature Distribution during Different Circulation Time under Multi-Pressure System When Overflow Rate Is Greater Than Leakage Rate
4.3. Annulus Temperature Distribution under Multi-Pressure System, Only Overflow or Only Leakage
4.4. The Temperature Difference between inside the Drill String and in Annulus When Multi-Pressure System, Only Leakage or Only Overflow Occurs
4.5. Bottom Hole Temperature Distribution When Multi-Pressure System, Only Overflow or Only Loss Circulation Occurs
4.6. Annulus Temperature Distribution at Different Overflow and Leakage Rates When Multi-Pressure System Exists
5. Analysis of the Influence of Coupled Temperature and Pressure on Viscosity and Density of Drilling Fluid
5.1. Normal Circulation
5.2. Under Multi-Pressure System
6. Analysis of Key Factors Influencing Bottom-Hole Pressure under Multi-Pressure System
6.1. Normal Circulation
6.2. Under Multi-Pressure System
7. Conclusions
- (1)
- As the circulation time increases, annulus temperature decreases gradually in the deeper part and increases gradually in the shallower part, no matter where the multi-pressure system is located.
- (2)
- When the multi-pressure system is located in the middle formation from 2500 m to 3500 m, annulus temperature in this area is most affected; however, the annulus temperature above 2000 m and below 4000 m is almost unaffected. If the multi-pressure system is located at the bottom hole, the annulus temperature from the bottom hole to the mud line is affected, and the temperature above the mud line is basically unchanged.
- (3)
- Whenever overflow occurs, the annulus temperature increases, or leakage occurs, the annulus temperature decreases. However, the annulus temperature increases the most when only overflow occurs and decreases the most when only leakage occurs.
- (4)
- Compared with the normal circulation, the temperature difference between inside drill string and in annulus in the middle well depth is more affected than in other areas along the borehole no matter where the multi-pressure system is located. What is more, only overflow or only leakage has the largest influence on temperature difference.
- (5)
- If the overflow rate is constant and leakage rate keeps increasing, then the annulus temperature gradually decreases; otherwise, it keeps rising at the same depth.
- (6)
- During normal circulation, bottom-hole pressure increases with increase of pump rate and decreases with the increase of inlet temperature. When the overflow rate is greater than leakage rate, the density of drilling fluid and bottom-hole pressure increases the most, and the only leakage has the least increase; the effect of the other cases listed on bottom-hole pressure is between them.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| hpi | convective heat transfer coefficient of drill string inside wall, W/(m2·°C) |
| hpo | convective heat transfer coefficient of drill string outside wall, W/(m2·°C) |
| hw | convective heat transfer coefficient of the borehole, W/(m2·°C) |
| Uap | the comprehensive convective heat transfer coefficient between drilling fluid in the drill string and drilling fluid in the annulus, W/(m2·°C) |
| Uaf | the comprehensive convective heat transfer coefficient between drilling fluid in the annulus and the formation, W/(m2·°C) |
| λw | heat conductivity coefficient of borehole, W/(m·°C) |
| λp | heat conductivity coefficient of drill string, W/(m·°C) |
| λf | heat conductivity coefficient of formation, W/(m·°C) |
| λcem | heat conductivity coefficient of cement sheath, W/(m·°C) |
| λeff | effective heat conductivity coefficient of formation, W/(m·°C) |
| λl | heat conductivity coefficient of fluid in the formation, W/(m·°C) |
| λ2 | heat conductivity coefficient of mixed fluid in annulus, W/(m·°C) |
| dpi | inside diameter of drill string, mm |
| dcemi | inside diameter of cement sheath, mm |
| dcemo | outside diameter of cement sheath, mm |
| dpo | outside diameter of drill string, mm |
| Tp | drilling fluid temperature in drill string, °C |
| Tpi | inside wall temperature of drill string, °C |
| Tpo | outside wall temperature of drill string, °C |
| Ta | drilling fluid temperature in annulus, °C |
| Tw | wall temperature of the well, °C |
| Tf | temperature of the formation, °C |
| Tsurf | surface temperature, °C |
| T0 | bottom-hole temperature inside the drill string, °C |
| T1 | bottom-hole temperature of the drill string, °C |
| T2 | bottom-hole temperature in annulus, °C |
| T3 | seawater temperature, °C |
| Tin | inlet temperature of the drill string, °C |
| ρs | density of seawater, kg/m3 |
| ρp | density of the drilling fluid inside the drill string, kg/m3 |
| ρa | density of the drilling fluid in annulus, kg/m3 |
| ρeff | effective fluid density with in the formation, kg/m3 |
| ρm | mixed fluid density within the formation, kg/m3 |
| ρ0 | original density of the drilling fluid inside the drill string, kg/m3 |
| ρi | density of each fluid phase, kg/m3 |
| cs | specific heat capacity of seawater, J/(kg·°C) |
| cp | specific heat capacity of the drilling fluid inside the drilling string, J/(kg·°C) |
| ca | specific heat capacity of the drilling fluid in the annulus, J/(kg·°C) |
| ceff | specific heat capacity of fluid information, J/(kg·°C) |
| Qcp | friction heat source of the drilling fluid inside the drill string, W/m3 |
| Qca | friction heat source of the drilling fluid in the annulus, W/m3 |
| Q′ca | friction heat source of the drilling fluid in the annulus of the multi-system pressure, W/m3 |
| Qm | pump rate of the drilling fluid inside the drill string, m3/s |
| Qa | pump rate of the drilling fluid in the annulus, m3/s |
| Qk | flow rate of overflow of fluid in the formation, m3/s |
| Ql | flow rate of leakage of fluid in the formation, m3/s |
| φ | porosity of formation rock |
| va | flow rate of drilling fluid in annulus, m/s |
| vkk | the flow rate of overflow of each sublayer in a multi-pressure system, m/s |
| vll | the flow rate of leakage of each sublayer in a multi-pressure system, m/s |
| vi | the flow rate of each fluid phase, m/s |
| Ai | the area of the flow cross section, m2 |
| K | absolute permeability of isotropic porous medium |
| K1 | relative permeability |
| P | intrinsic average pressure of formation, Pa |
| Pfi | Annulus friction pressure loss |
| H | well depth, m |
| h | the depth of a well at a given location, m |
| G | geothermal gradient, °C/m |
| yml | depth of mudline |
| μ | velocity in the x direction, m/s |
| vr | seepage velocity of fluid information, m/s |
| χ | experimental measurement coefficient |
Appendix A. Model Solution

Appendix A.1. Heat Transfer Model Discretization of Drilling Fluid in Drill String
Appendix A.2. Heat Transfer Model Discretization of Drilling Fluid in Annulus
Appendix A.2.1. The Multi-Pressure System Is Located in the Middle Section of the Formation
Appendix A.2.2. When the Multi-Pressure System Is Located at Bottom Hole, the Whole Annulus Is Affected by the Multi-Pressure System. Therefore, Its Heat Transfer Model and Discrete Method Are the Same as the Upper Annulus Model when the Multi-Pressure System Appears in the Middle Open Hole Formation
Appendix A.3. The Heat Transfer Mode in the Formation and Seawater
Appendix A.4. Heat Transfer Equation of Boundary between Strata and Annulus Can Be Written as Follows
Appendix A.5. The Dispersion of the Momentum Equation

References
- Zhang, Z.; Xiong, Y.M.; Gao, Y.; Liu, L.M.; Wang, M.; Peng, G. Wellbore temperature distribution during circulation stage when well-kick occurs at bottom-hole from the bottom-hole. Energy 2018, 164, 964–977. [Google Scholar] [CrossRef]
- Wiktorski, E.; Cobbah, C.; Sui, D.; Khalifeh, M. Experimental study of temperature effects on wellbore material properties to enhance temperature profile modeling for production wells. J. Pet. Sci. Eng. 2019, 176, 689–701. [Google Scholar] [CrossRef]
- Abdollahi, J.; Dubljevic, S. Transient Fluid Temperature Estimation in Wellbores. IFAC Proc. Vol. 2013, 46, 108–113. [Google Scholar] [CrossRef]
- Hasan, R.; Kabir, C.S. Wellbore heat-transfer modelling and applications. J. Pet. Sci. Eng. 2012, 86–87, 127–136. [Google Scholar] [CrossRef]
- Yang, M.; Zhao, X.; Meng, Y.; Li, G.; Zhang, L.; Xu, H.; Tang, D. Determination of transient temperature distribution inside a wellbore considering drill string assembly and casing program. Appl. Therm. Eng. 2017, 118, 299–314. [Google Scholar] [CrossRef] [Green Version]
- Jia, H.J.; Meng, Y.F.; Li, G.; Su, G.; Zhao, X.Y.; Wei, N.; Song, W. Research on overflow accompanied with lost circulation during drilling of gas formation with multi-pressure system. Fault-Block Oil Gas. 2012, 19, 360–363. [Google Scholar]
- Ramey, H.J., Jr. Wellbore heat transmission. J. Pet. Technol. 1962, 14, 427–435. [Google Scholar] [CrossRef]
- Holmes, C.S.; Swift, S.C. Calculation of circulating mud temperatures. J. Pet. Technol. 1970, 22, 670–674. [Google Scholar] [CrossRef]
- Kabir, C.S.; Hasan, A.R.; Kouba, G.E.; Ameen, M. Determining circulating fluid temperature in drilling, workover, and well control operations. SPE Drill. Complet. 1996, 11, 74–79. [Google Scholar] [CrossRef]
- You, J.; Rahnema, H.; McMillan, M.D. Numerical modeling of unsteady-state wellbore heat transmission. J. Nat. Gas Sci. Eng. 2016, 34, 1062–1076. [Google Scholar] [CrossRef]
- Raymond, L.R. Temperature distribution in a circulating drilling fluid. J. Pet. Technol. 1969, 21, 333–341. [Google Scholar] [CrossRef]
- Marshall, D.W.; Bentsen, R.G. A computer model to determine the temperature distributions in a wellbore. J. Can. Pet. Technol. 1982, 21, 63–75. [Google Scholar] [CrossRef]
- Santoyo-Gutierrez, E.R. Transient Numerical Simulation of Heat Transfer Processes During Drilling of Geothermal Wells. Ph.D. Thesis, University of Salford, Salford, UK, 1 September 1997. [Google Scholar]
- García, A.; Santoyo, E.; Espinosa, G.; Hernandez, I. Estimation of temperatures in geothermal wells during circulation and shut-in in the presence of lost circulation. Transp. Porous Media 1998, 33, 103–127. [Google Scholar] [CrossRef]
- Espinosa-Paredesa, G.; Garcia, A.; Santoyo Hernandez, E. A computer program for estimation of fully transient temperatures in geothermal wells during circulation and shut-in. Comput. Geosci. 2001, 27, 327–344. [Google Scholar] [CrossRef]
- Yang, M.; Tang, D.; Chen, Y.; Li, G.; Zhang, X.; Meng, Y. Determining initial formation temperature considering radial temperature gradient and axial thermal conduction of the wellbore fluid. Appl. Therm. Eng. 2019, 147, 876–885. [Google Scholar] [CrossRef]
- Zheng, Z.; Xiong, Y.M.; Guo, F. Analysis of Wellbore Temperature Distribution and Influencing Factors During Drilling Horizontal Wells. J. Energy Resour. Technol. 2018, 140, 092901. [Google Scholar] [CrossRef]
- Wang, X.R.; Sun, B.J.; Luo, B.Y. Transient temperature and pressure calculation model of a wellbore for dual gradient drilling. Appl. Therm. Eng. 2018, 30, 701–714. [Google Scholar] [CrossRef]
- Farahani, H.S.; Yu, M.; Miska, S.; Takach, N.; Chen, G. Modeling Transient Thermo-Poroelastic Effects on 3D Wellbore Stability. In Proceedings of the SPE Technical Conference and Exhibition, San Antonio, TX, USA, 24–27 September 2006. [Google Scholar]
- Song, X.C.; Guan, Z.C. Full Transient Analysis of Heat Transfer During Drilling Fluid Circulation in Deep-Water Wells. Acta Pet. Sin. 2011, 32, 704–708. [Google Scholar]
- Zheng, Z.; Xiong, Y.M.; Mao, L.J.; Lu, J.S.; Wang, M.H.; Peng, G. Transient temperature prediction models of wellbore and formation in wellkick condition during circulation stage. J. Pet. Sci. Eng. 2019, 175, 266–279. [Google Scholar] [CrossRef]
- Chen, Y.H.; Yu, M.J.; Miska, S.; Zhou, S.H.; Al-Khanferi, N.; Ozbayoglu, E. Fluid flow and heat transfer modeling in the event of lost circulation and its application in locating loss zones. J. Pet. Sci. Eng. 2017, 148, 1–9. [Google Scholar] [CrossRef]
- Wang, L.Y.; Wang, K.Q. A new method for calculating thermal conductivity of mixed liquid. Chem. Eng. 1999, 27, 45–51. [Google Scholar]
- Yang, H.W.; Li, J.; Liu, G.H.; Wang, C.; Li, M.; Jiang, H. Numerical analysis of transient wellbore thermal behavior in dynamic deepwater multi-gradient drilling. Energy 2019, 179, 138–153. [Google Scholar] [CrossRef]
- Arnold, F.C. Temperature variation in a circulating wellbore fluid. J. Energy Res. Technol. 1990, 112, 79–83. [Google Scholar] [CrossRef]
- Edwardson, M.J.; Girner, H.M.; Parkinson, H.R.; Williamson, C.D.; Matthews, C.S. Calculation of formation temperatures disturbances caused by mud circulation. J. Pet. Technol. 1962, 14, 416–426. [Google Scholar] [CrossRef]
- Deng, S.; Fan, H.; Tian, D.; Liu, Y.; Zhou, Y.; Wen, Z.; Ren, W. Calculation and application of safe mud density window in deepwater shallow layers. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 2–5 May 2016. [Google Scholar]
- Li, M.B.; Liu, G.H.; Li, J.; Zhang, T.; He, M. Thermal performance analysis of drilling horizontal wells in high temperature formations. Appl. Therm. Eng. 2015, 78, 217–227. [Google Scholar] [CrossRef]
- Zahedi, G.; Karami, Z.; Yaghoobi, H. Prediction of hydrate formation temperature by both statistical models and artificial neural network approaches. Energy Convers. Manag. 2009, 50, 2052–2059. [Google Scholar] [CrossRef]
- Yang, H.W.; Li, J.; Liu, G.H. Development of transient heat transfer model for controlled gradient drilling. Appl. Therm. Eng. 2019, 148, 331–339. [Google Scholar] [CrossRef]
- Yang, M.; Li, X.X.; Deng, J.M.; Meng, Y.F.; Li, G. Prediction of wellbore and formation temperatures during circulation and shut-in stages under kick conditions. Energy 2015, 91, 1018–1029. [Google Scholar] [CrossRef]
















| Parameters | Value | Parameters | Value |
|---|---|---|---|
| Well depth, m | 5094 | Drilling fluid flow rate, m3/s | 0.02 |
| Water depth, m | 1521 | ROP, m/h | 3.05 |
| Open hole diameter, mm | 215.9 | Surface temperature, °C | 20 |
| Inlet temperature, °C | 15 | Geothermal gradient, °C | 0.024 |
| Drilling fluid viscosity, mPa·s | 10 | Fluid density in formation, kg/m3 | 1100 |
| Medium | Density, kg/m3 | Specific Heat, J/(kg·K) | Coefficient of Heat Conduction W/(m·K) |
|---|---|---|---|
| Drilling fluid | 1180 | 3935 | 1.75 |
| Drill string | 7850 | 400 | 43.7 |
| Drill collars | 8910 | 400 | 43.7 |
| Fluid in formation | 1150 | 4200 | 0.8 |
| Seawater | 1050 | 4128 | 0.6 |
| Casing | 8300 | 400 | 43.7 |
| Cement | 2140 | 900 | 0.85 |
| Rock | 2640 | 853 | 2.3 |
| Parameters | Inside Diameters (mm) | Outside Diameters (mm) |
|---|---|---|
| Drill pipe | 108 | 127 |
| Drill collar | 80 | 171 |
| First casing | 486 | 508 |
| Second casing | 317 | 339 |
| Third casing | 221 | 245 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, R.; Li, J.; Liu, G.; Yang, H.; Jiang, H. Analysis of Coupled Wellbore Temperature and Pressure Calculation Model and Influence Factors under Multi-Pressure System in Deep-Water Drilling. Energies 2019, 12, 3533. https://doi.org/10.3390/en12183533
Zhang R, Li J, Liu G, Yang H, Jiang H. Analysis of Coupled Wellbore Temperature and Pressure Calculation Model and Influence Factors under Multi-Pressure System in Deep-Water Drilling. Energies. 2019; 12(18):3533. https://doi.org/10.3390/en12183533
Chicago/Turabian StyleZhang, Ruiyao, Jun Li, Gonghui Liu, Hongwei Yang, and Hailong Jiang. 2019. "Analysis of Coupled Wellbore Temperature and Pressure Calculation Model and Influence Factors under Multi-Pressure System in Deep-Water Drilling" Energies 12, no. 18: 3533. https://doi.org/10.3390/en12183533
APA StyleZhang, R., Li, J., Liu, G., Yang, H., & Jiang, H. (2019). Analysis of Coupled Wellbore Temperature and Pressure Calculation Model and Influence Factors under Multi-Pressure System in Deep-Water Drilling. Energies, 12(18), 3533. https://doi.org/10.3390/en12183533