1. Introduction
Over the last decade, crude oil and gas production from hydrofractured shales in the United States has accounted for most of the net increase of global crude oil production. Therefore, it is important to have a reliable, quantitative method for delineating the possible futures oil and gas production in the data-rich US shales. The current industry-standard methods of forecasting production from shales are variants of the empirical decline curve analysis (DCA) [
1], developed 75 years ago. Lately, some of the more sophisticated methods, for example, Fractional Decline Curve [
2] have become popular.
Unlike other analytical and numerical methods that require numerous reservoir parameters and a lengthy calculation or simulation time, DCA only requires production data to predict future production by extrapolating oil or gas rate observed in a boundary-dominated flow regime. Because of DCA’s simplicity, most petroleum engineers adopt it for reserve assessment in shales, including Estimated Ultimate Recovery (EUR) predictions from USGS [
3,
4] and EIA [
5].
USGS first split the Bakken region into 6 assessment units (AUs) and defined sweet spots. Then, they calculated the number of wells that could be drilled in each AU by dividing its total area with the average drainage area per well. In parallel, they used DCA to calculate the average EURs for sweet spots and other areas. The 7.4 billion barrels of undiscovered technically recoverable oil was obtained by multiplying the total number of wells that could be drilled in each AU with the corresponding average EUR multiplied by the untested fraction of that AU. EIA used a similar approach by dividing the Bakken region into 5 AUs and refining them by counties to determine the infill well potential. Both USGS and EIA predictions were assessed by Hughes [
6,
7,
8,
9]. We predict that the undiscovered, technically recoverable oil in the Bakken is 2 billion bbls in the core area and it might be 6 billion bbls in the noncore area (
Figure 1) or
8 billion barrels in total.
Most shale wells do not reach the boundary-dominated flow regime for their entire production lives because of the vanishing matrix permeability. Thus, the traditional DCA frequently overestimates EURs of shale wells. To address this issue, many authors have suggested improved DCA methods, specific to shale wells: the Power Law Exponential Decline [
10], the Stretched Exponential Decline [
11], the Logistic Growth Model [
12], the Extended Exponential DCA [
13], and the Extended Hyperbolic DCA [
14]. To make things worse, the empirical DCA fits of particular wells are ill-suited to forecasting production from a wide area of a given shale play in which reservoir properties vary and uncertainties abound. Therefore, some authors have developed probabilistic models to introduce a range of possible outcomes into their production forecasts [
15,
16,
17,
18,
19,
20]. The most common assumption is that well productivities in shales are log-normally distributed.
In this paper, we adopt a hybrid data-driven
and physics-based method of predicting oil or gas production in shales that has been introduced in our previous work [
21,
22]. Here, we consider only black oil production. First, we identify play
regions in which reservoir quality is similar, see
Figure 1. In each region, we identify well
classes by different completion technologies. Finally, a well class in a region constitutes a well
sample. We ensure that oil production from all wells in each sample is statistically uniform, that is, has a unimodal distribution. For each well sample, we then identify well
cohorts with
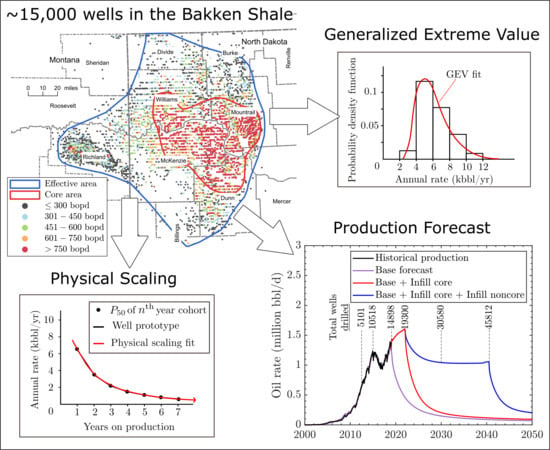
at least years on production. In general, well cohorts contain different sets of wells that satisfy the minimum time on production required for each cohort. It turns out that each cohort of wells is superbly characterized by its unique Generalized Extreme Value (GEV) distribution (see
Appendix A) of annualized well rates or cumulative well production. Different cohorts in the same sample have different GEV distributions, each with its unique expected value, median and mode. Here we choose the somewhat better GEV fits of the production rate distributions. Each GEV distribution is statistically superior to the corresponding log-normal distribution at the 95% confidence level. When we plot the expected values of the GEV distributions of all wells cohorts in a sample versus elapsed time of production, we obtain this sample’s average
statistical well prototype that is purely field data-driven.
Now we fit each statistical well prototype with a physical scaling curve that extends this prototype to 30 years on production. The physical scaling curves are based on an analytical solution of the pressure diffusion equation in the hydrofractured horizontal shale well geometry. In previous papers, we comprehensively detailed the physical scaling solutions for shale gas wells [
23,
24] and shale oil wells [
22,
25]. Late-time flow from outer reservoir encompassing the stimulated reservoir volume (SRV) [
26] was also quantified. We have verified that our physical scaling is equivalent to detailed numerical reservoir simulations [
27]. This scaling is much simpler to set up and runs almost infinitely faster than the corresponding reservoir simulations.
At this point, for each well sample in every play region, we have obtained a unique hybrid mean () well prototype with 30 years on production. In each play region, we know how many wells were drilled and completed each month up until current time. We then multiply each well prototype by the number of wells completed per month and stack them up to represent the total historical field rate and future production decline. In this manner, we obtain a ‘base’ case forecast for all existing wells. This base case forecast is a ‘do nothing’ scenario with no new wells drilled in the future. For all other forecasts of future field production rate, we first determine the infill potential or the number of wells that can be drilled in the future without causing significant interwell pressure interference (fracture hits). We cover each region with a fish-net grid that consists of one-square-mile pixels. We then calculate the infill potential as the number of wells that can be drilled so that the total number of wells in each pixel is less than the maximum allowable number of wells without fracture hits. Next, based on the infill potentials for all regions, we create future drilling programs to obtain plausible forecasts of oil or gas production. Based on current rig count in the Bakken, we assume a constant overall drilling rate. Finally, we assign the correct well prototype to every future well that will be drilled during each month of a postulated drilling schedule, and sum them up to obtain a forecast scenario.
In this paper, we select the Bakken shale, the current second-largest oil producer in the U.S. with 1.5 million bbl of oil per day, as an illustration. Being one of the oldest shale oil plays, Bakken has been a field laboratory to test drilling and completion technologies and increase well productivity. Currently, Bakken has ∼15,000 active hydrofractured horizontal wells with a few wells that have 18 years of production data. In a previous paper [
22], we scaled well-by-well all ∼15,000 wells in the Bakken. We accounted for well refracturing and/or changes in downhole pressure. It turns out that the 12 well prototypes obtained with our hybrid GEV–physical scaling method are as good in duplicating the total field rate as the super-precise scaling of each individual well in our previous work [
22]. Given the results of our analyses that are free of bias, policy-makers should not assume that the production boom in the Bakken shale will last decades longer.
3. Discussion
We have presented an alternative to the current industry-standard empirical forecasts of oil production from hydrofractured horizontal wells in shales. With our hybrid modeling approach, we have matched current oil production in the Bakken rather accurately. We have also delivered an optimal prediction of possible futures of the Bakken shale play for up to three decades.
Our Bakken oil forecasting method extends the previous work on predicting fieldwide gas production in the Barnett shale [
21] and merges it with our new scaling of oil production in the Bakken [
22]. Our field data-driven statistical well prototypes are conditioned by well attrition, hydrofracture deterioration, pressure interference, well interference, progress in technology, and so forth. With
no physical scaling, these prototypes follow the exact physics of linear transient oil flow with pressure interference. Therefore these statistical well prototypes serve as templates to calibrate the parameters of our physical scaling model (
and
[
23,
24] and obtain a
smooth time-extrapolation of oil production that is mechanistic and not merely an empirical decline curve. At late times, we add to our extended prototypes some radial inflow from the outside of well SRVs [
26].
The extended
well prototypes in
Figure 6 can be used to compare ultimate recovery in each of the static regions we have identified in the Bakken. The lower bounds are the extended
prototypes without exterior flow (red lines). In most cases, wells completed in the upper Three Forks reservoir are somewhat less productive than those in the Middle Bakken reservoir. The reasons for this difference are: (1) higher water saturation and water cut in Three Forks, (2) faster decline rate (lower
) and (3) lower initial oil in place (lower
) [
22]. This difference is consistent with the stratigraphic column of the Bakken total petroleum system, where Middle Bakken is sandwiched between two world-class source rocks with 10% TOC, the Upper Bakken Shale and the Lower Bakken Shale. On the other hand, the Three Forks formation is below the Lower Bakken Shale member and is exposed to water-bearing formations beneath [
3,
28,
29,
30]. For the same reasons, the
core and
effective drilling areas in the Three Forks are smaller than those in the Middle Bakken.
In both reservoirs, production from the
core areas is superior to that from the
noncore areas. The core area located in the center of Williston Basin has been known as the most oil-prolific location in the Bakken region in North Dakota [
3,
28,
29,
30]. Since the 1950s, oil has been produced there in the thickest, naturally fractured Middle Bakken formation in the Nesson anticline. One inexpensive vertical well drilled in the core area in the 1950s has had ultimate recovery of 200 kbbl, the same as a
$10 million hydrofractured horizontal well drilled in the Middle Bakken noncore area nowadays. The noncore areas are less productive because the three Bakken formations: Upper, Middle and Lower Bakken are pinching out upward (are thinner and less mature) near the edges of the Williston basin. Consequently, the noncore areas are producing more water than oil, with watercut exceeding 50% on average.
The newly completed wells have much higher initial oil rates than the older ones, because they have: (1) longer lateral lengths, (2) bigger hydraulic fractures and (3) more fracture stages [
22,
31,
32,
33,
34]. However, the newly completed wells decline faster and have essentially the same ultimate recovery as the older wells. The reasons for this behavior have been described elsewhere [
35]. Interestingly, in most cases, older wells completed in 2000–2012 have higher ultimate recovery than newer ones, even though their initial production rates are lower. These older wells might have been drilled in the best locations ever in the Bakken region. In addition, shorter lateral lengths and fewer fracture stages may help in maintaining a stable pressure drawdown and prevent reservoir degassing that is unfavorable for future production. For comparison, the average lateral length in 2005 was 5000 ft while the average lateral length in 2019 doubled to 10,000 ft. Historically, the number of hydrofracture stages in the Bakken has increased over time from 8 stages in 2007 [
36] to 18 stages in 2009 [
31], 35 stages in 2016 [
32] and to as many as 60 stages in 2019 [
33].
According to our records, more than 90% of the wells completed after 2017 are located in the core areas only. Operators have learned to drill only the best parts of the Williston Basin and avoid the less mature noncore areas. However, after calculating the infill potentials of all areas, we predict that by 2021 there will be no well locations left for future drilling in the core areas. Assuming a constant current drilling rate of 120 wells per month, the total field oil rate in the Bakken will reach record level of about 1.6 million bbl/d in 2021. Without further drilling, production will decline by one-half within a year. Later, operators will be forced to drill in the less productive, high watercut noncore areas along the edges of the Williston Basin. Our findings suggest that policy-makers should not assume that the shale oil boom in the Bakken will last for several decades longer. We recommend that operators not focus only on increasing the initial oil rate. Maintenance of reservoir pressure above the bubble point by preventing over-drilling is key to increasing ultimate oil recovery.